Harmonic Excitation
Objective: Comparison of the calculated response spectrum with the exact analytical solution.
Initial data files:
Sin.spc — accelerogram
Sin.txt — lists of frequencies
Sin.xls — comparison of results
sinReport.doc — report
Problem formulation: A sinusoidal accelerogram is considered, i.e. the acceleration at time t is sin(t). A response spectrum calculated by the program and obtained analytically is analyzed. We consider the case when the damping ratio is 15% of the critical value (the logarithmic decrement is 0.953263).
Comparison of solutions:
Response spectra obtained numerically and analytically are given in the figure below
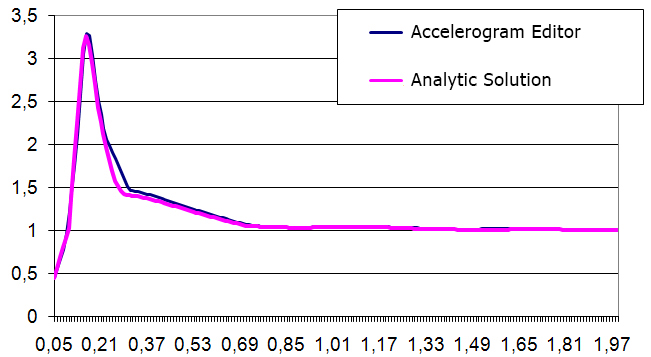
The value of the maximum acceleration in both cases is achieved at the same frequency. The values of maximum accelerations differ by 1,2%.
Notes: The equation of motion
\[ \ddot{{x}}+2\beta \omega \dot{{x}}+\omega^{2}x=-a_{0} \sin (\theta t) ,\] \[ x(0)=\dot{{x}}(0)=0. \]
The analytical solution of this equation is as follows
\[ x(t)=e^{-\beta \omega t}\left( {A\sin \omega_{D} t+B\cos \omega_{D} t} \right)+C\cos \theta t+D\sin \theta t ,\]
where
\[ \omega_{D} =\omega \sqrt {1-\beta^{2}} , \] \[ C=a_{0} \frac{2\beta \omega \theta }{\left( {\omega^{2}-\theta^{2}} \right)^{2}+(2\beta \omega \theta )^{2}}, \] \[ D=a_{0} \frac{\theta^{2}-\omega^{2}}{\left( {\omega^{2}-\theta^{2}} \right)^{2}+(2\beta \omega \theta )^{2}}, \] \[ B=-C, \] \[ A=-\beta C-D\theta /\omega_{D} . \]