Simply Supported Beam on the Elastic Horizontal Subgrade Subjected to a Vertical Uniformly Distributed Load, Concentrated Vertical Force and Bending Moment

Objective: Determination of the stress-strain state of a simply supported beam on the elastic horizontal subgrade subjected to a vertical uniformly distributed load, concentrated force and bending moment.

Initial data files:

File name	Description
SSLL16_var_1_v11.3.spr	Design model – bar elements on the elastic subgrade
SSLL16_var_2_v11.3.spr	Design model – bar elements on elastic supports in the form of elements of constraints of finite rigidity of type 51

Problem formulation: The simply supported beam on the elastic horizontal subgrade with the stiffness k constant along the length is subjected to a vertical uniformly distributed load P, concentrated vertical force F, applied in the middle of the span (point D) and concentrated bending moments -C and C, applied at the edges (points A and B). Determine the vertical displacement Z in the middle of the beam span (point D), rotation angles UY of the beam edges (points A and B), as well as the bending moment M in the middle of the beam span and the shear force Q at the edge of the beam.

References: M. Courtand et P. Lebelle, Formulaire du beton arme, t.2, Paris, Eyrolles,1976, p. 385.

Initial data:

E = 2.1∙1011 Pa	- elastic modulus;
l = 0.5∙π∙(10.0)0.5 = 4.967294133 m	- beam length;
b = 1.0 m	- beam width;
Iy = 1.0∙10-4 m4	- cross-sectional moment of inertia of the beam;
kz = 8.4∙105 N/m3	- subsoil parameter;
P = 5.0∙103 N/m	- value of the vertical uniformly distributed load;
F = 1.0∙104 N	- value of the concentrated vertical force;
C = 1.5∙104 N∙m	- value of the concentrated bending moment.

 

Finite element model: Two variants of the design model are considered.

 

Variant 1:

Design model – grade beam / plate, 24 bar elements of type 3 on the elastic subgrade directed along the Z1 axis of the local coordinate system. Boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z for roller support nodes. Number of nodes in the design model – 25.

Variant 2:

Design model – grade beam / plate, 24 bar elements of type 3 on the elastic supports in the form of 25 elements of constraints of finite rigidity of type 51 directed along the Z axis of the global coordinate system. Stiffness of intermediate elastic supports: k_z∙b∙l/24 = 173855 N/m, stiffness of end elastic supports: 0.5∙k_z∙b∙l/12 = 86928 N/m. Boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z for roller support nodes. In order to prevent the dimensional instability of the system, a constraint in the direction of the degree of freedom UX is imposed along the beam symmetry axis and the minimum torsional stiffness of the beam is introduced GI_x = 1.0 N∙m2. Number of nodes in the design model – 25.

Results in SCAD

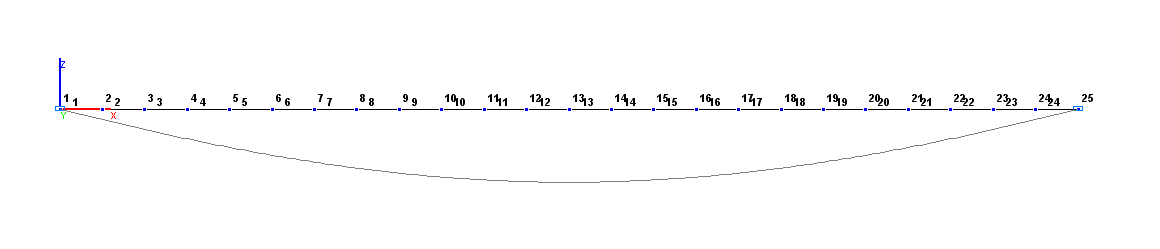
Design and deformed models. Variant 1

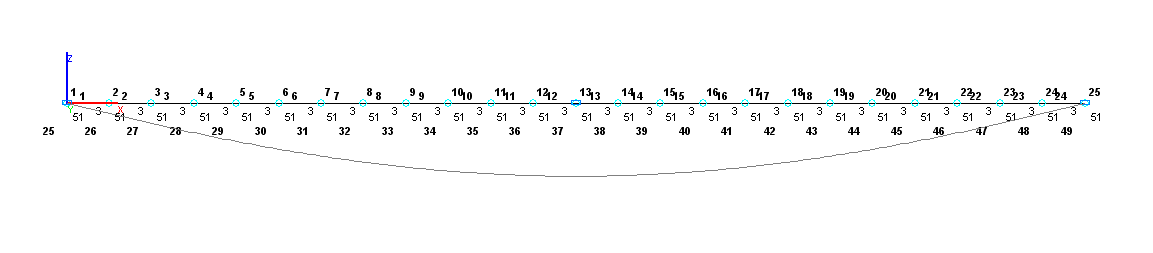
Design and deformed models. Variant 2

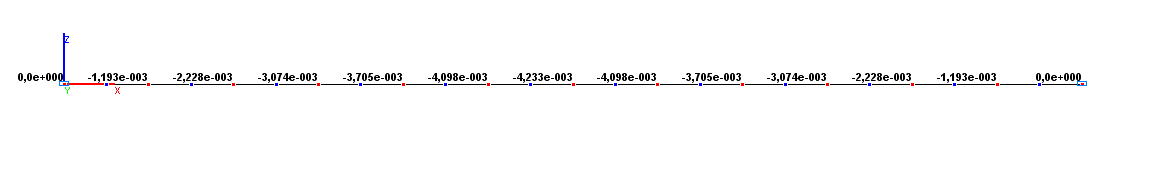
Values of vertical displacements Z (m) for the design model according to variant 1

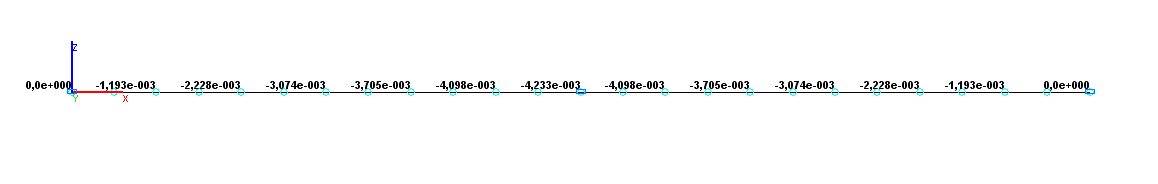
Values of vertical displacements Z (m) for the design model according to variant 2

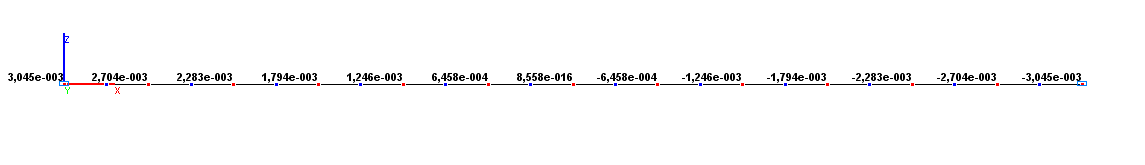
Values of rotation angles UY (rad) for the design model according to variant 1

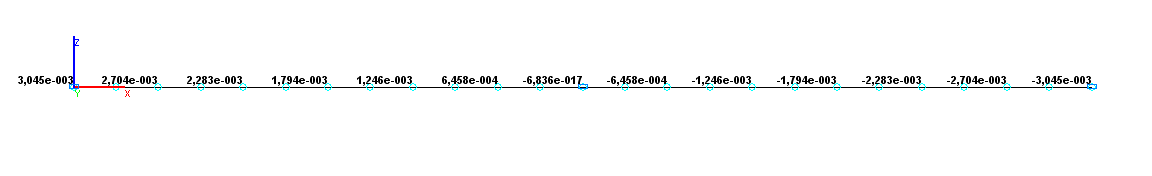
Values of rotation angles UY (rad) for the design model according to variant 2

Values of bending moments M (N∙m) for the design model according to variant 1

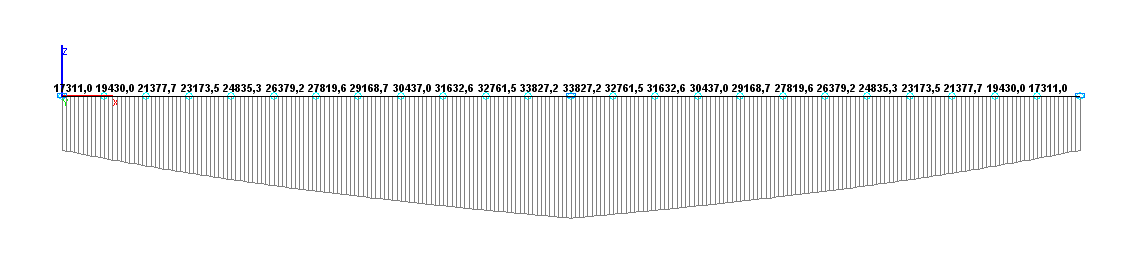
Values of bending moments M (N∙m) for the design model according to variant 2

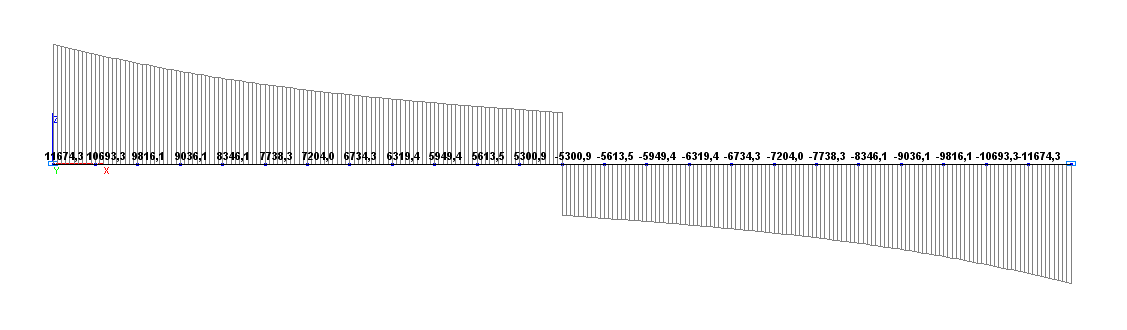
Values of shear forces Q (N) for the design model according to variant 1

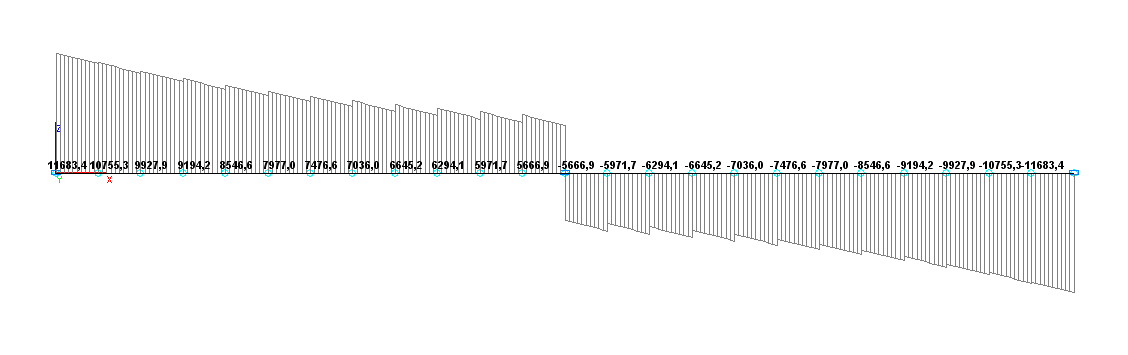
Values of shear forces Q (N) for the design model according to variant 2

Comparison of solutions:

Parameter	Theory	SCAD DM according to variant 1	Deviations, %	SCAD DM according to variant 2	Deviations, %
Vertical displacement ZD, m	-4.233∙10-3	-4.233∙10-3	0.00	-4.233∙10-3	0.00
Rotation angle UYA, rad	3.045∙10-3	3.045∙10-3	0.00	3.045∙10-3	0.00
Bending moment MD, N∙m	33840.0	33839.9	0.00	33827.2	0.04
Shear force QA, N	11674.0	11674.3	0.00	11683.4	0.08