Replacement of a Column of a Two-Span Single-Storey Frame Subjected to a Constant Load

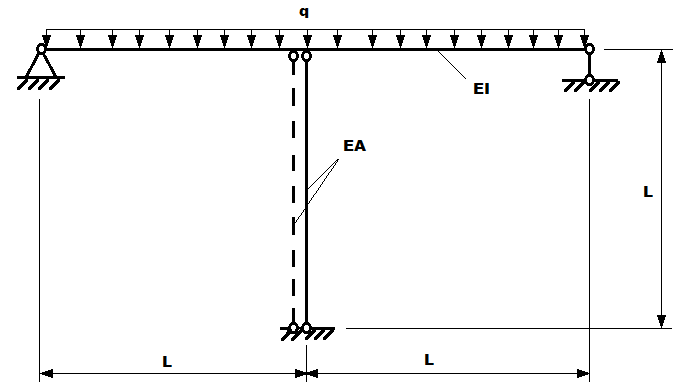
Objective: Determination of the internal forces in the elements of a two-span single-storey frame before and after the replacement of a column subjected to a constant load.

Initial data file: Rearrange_Frame.MPR

Problem formulation: The two-span girder of the frame simply supported at the ends with a middle support in the form of a hinged column is subjected to the constant uniformly distributed load. During the reconstruction the column is replaced by a column of the same rigidity in the following order: the replacing column is installed and then the original one is dismantled. Determine the maximum bending moments in the girder of the frame M_I, M_II and the longitudinal forces in the columns N_I, N_II before and after the replacement.

Initial data:

EF = 2.0·107 t	- axial stiffness of the girder and column cross-section;
EI = 1.2·108 t·m2	- bending stiffness of the girder and column cross-section;
L = 6.0 m	- girder span length and column height;
q = 4.0 t·m	- uniformly distributed constant vertical load applied to the girder spans.

 

Finite element model: Design  model – plane frame, elements of the girder – 24 bar elements of type 2, elements of the columns – 24 bar elements of type 2. The spacing of the finite element mesh along the longitudinal axes of the structural members is 0.5 m. The node of the left end of the girder is constrained in the directions of the degrees of freedom X, Z. The node of the right end of the girder is constrained in the direction of the degree of freedom Z. The nodes of the lower ends of the columns are constrained in the directions of the degrees of freedom X, Z. The elements of the upper ends of the columns have a hinge in the direction of the degree of freedom UY. Number of nodes in the design model – 37. Elements of the girder 1 – 24 and of the original column 25 – 36 are included in the first erection stage. Elements of the girder 1 – 24 and of the replacing column 37 – 48 are included in the second erection stage. The accumulated loading q is acting in both stages.

 

Results in SCAD

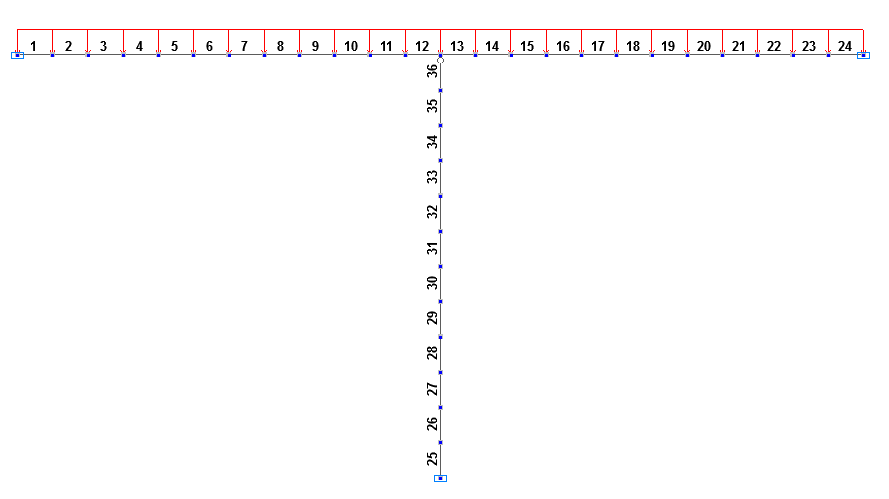
Design models in the first and second erection stages

 

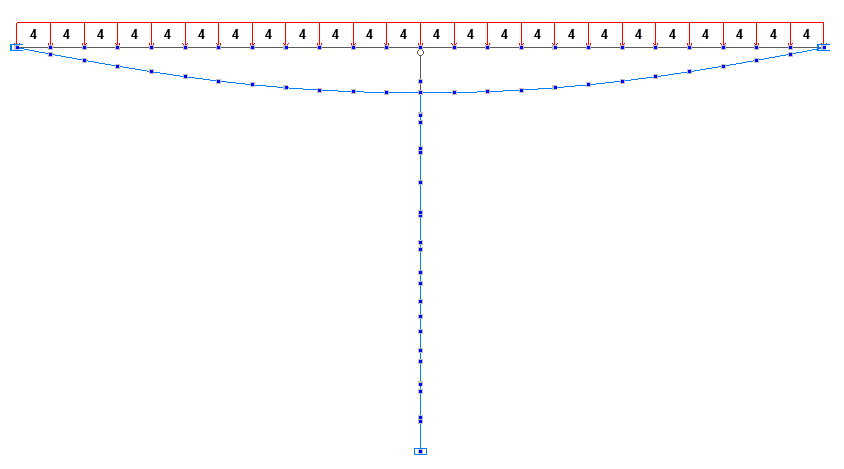
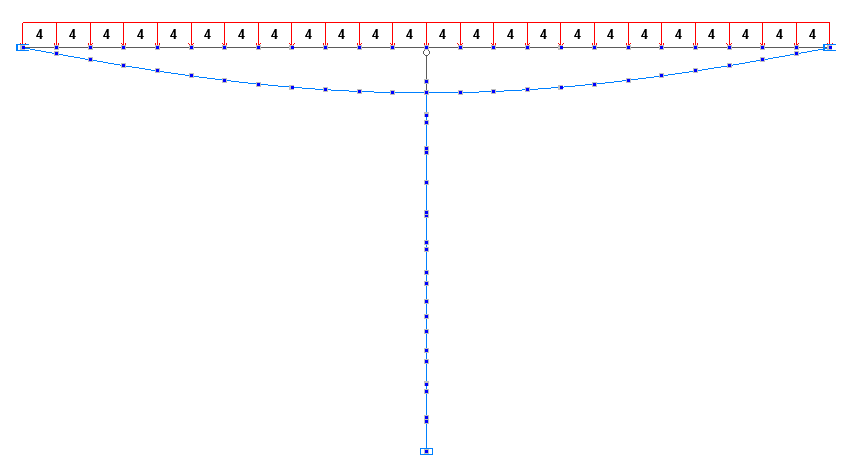
Deformed models in the first and second erection stages

 

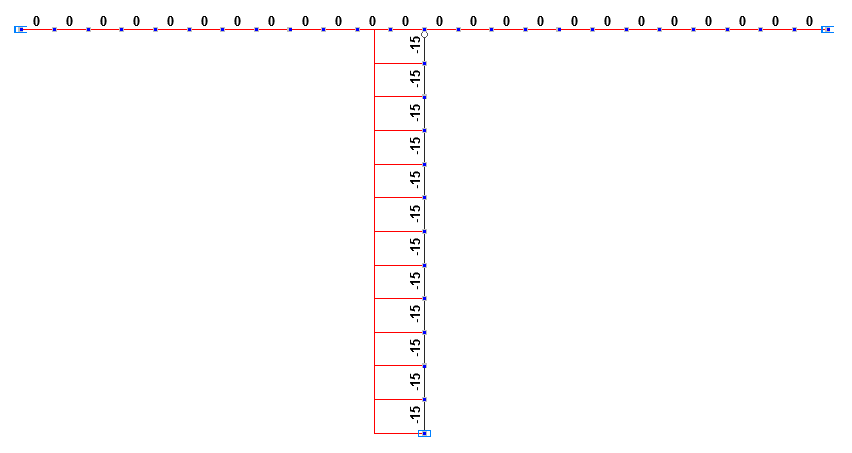
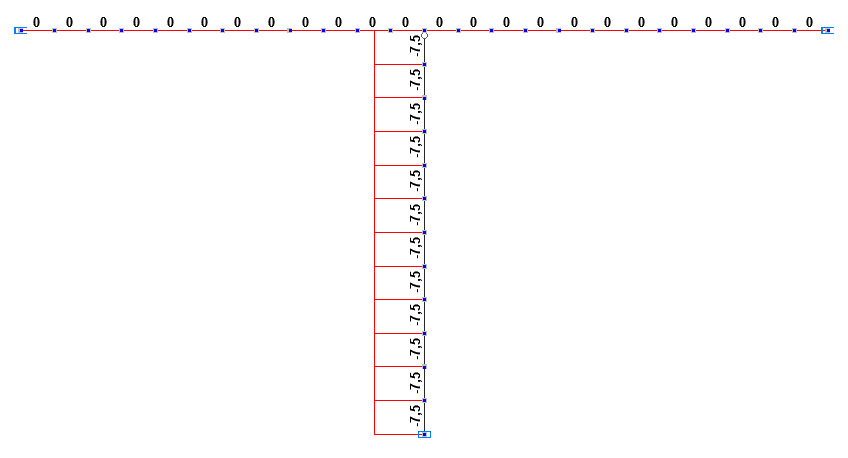
Longitudinal force diagrams N_I, N_II in the first and second erection stages (t)

 

Bending moment diagrams M_I, M_II in the first and second erection stages (t∙m)

 

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Maximum bending moment in the girder of the frame in the first erection stage MI, t∙m	34.03	34.03	0.00
Longitudinal force in the column of the frame in the first erection stage NI, t	-15.0	-15.0	0.00
Maximum bending moment in the girder of the frame in the second erection stage MII, t∙m	51.26	51.25	0.02
Longitudinal force in the column of the frame in the second erection stage NII, t	-7.5	-7.5	0.00

Notes: In the analytical solution the maximum bending moments in the girder of the frame M_I, M_II and the longitudinal forces in the columns N_I, N_II before and after the replacement are determined according to the following formulas:

\[ M_{I} =\frac{1}{2}\,\cdot \,q\,\cdot \,L^{2}-\frac{1}{2}\cdot \,q\,\cdot L\,\cdot \,\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}}+\frac{1}{8}\,\cdot \,q\,\cdot \,\left( {\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}}} \right)^{2} \] \[ N_{I} =-q\,\cdot \,\frac{\frac{5}{24}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{3}}{6\,\cdot \,EI}+\frac{L}{EA}} \] \[ M_{II} =\frac{441}{512}\,\cdot \,q\,\cdot \,L^{2}-\frac{21}{16}\,\cdot \,q\,\cdot \,L\,\cdot \,\frac{\frac{15}{96}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}}+\frac{1}{2}\,\cdot \,q\,\cdot \,\left( {\frac{\frac{15}{96}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}}} \right)^{2} \] \[ N_{II} =-\,q\,\cdot \,\frac{\frac{5}{48}\,\cdot \,\frac{L^{4}}{EI}}{\frac{L^{2}}{6\,\cdot \,EI}+\frac{L}{EA}} \]