Elastic Half-Space Subjected to a Transverse Load Uniformly Distributed over a Rectangular Surface. Love’s Problem
Objective: Determination of the stress-strain state of the elastic half-space subjected to a transverse load uniformly distributed over a rectangular surface in accordance with the spatial problem of the theory of elasticity.
Initial data files: Lave.SPR
Problem formulation: The elastic half-space is subjected to the transverse load q uniformly distributed over a rectangular surface. Determine:
- distribution of the normal stresses σx, σy, σz across the half-space;
- distribution of the tangential stresses τxy, τxz, τyz across the half-space;
- distribution of the displacements u, v, w across the half-space.
References: Z.G. Ter-Martirosyan, Soil Mechanics, Moscow, MGSU Publishing House of the Association of Construction Institutions of Higher Education, 2009, p. 204;
V.A. Florin, Fundamentals of Soil Mechanics, Volume 1, Leningrad, State Publishing House of Literature on Construction, Architecture and Building Materials, 1959, p. 123;
V.A. Florin, Fundamentals of Soil Mechanics, Volume 2, Leningrad, State Publishing House of Literature on Construction, Architecture and Building Materials, 1959, p. 24.
Initial data:
| E = 30000 kN/m2 | - elastic modulus of the half-space; |
| m = 0.3 | - Poisson’s ratio; |
| a = b = 2.0 m | - length of the half of the side of a rectangular loaded surface; |
| q = 100 kN/m2 | - transverse load q uniformly distributed over a rectangular surface. |
Finite element model: 96×96×48 m parallelepiped is analyzed. The design model (quarter of the parallelepiped cut off by the symmetry planes XOZ and YOZ) – general type system, elements of the elastic half-space – 138253 20-node isoparametric solid elements of type 37. The spacing of the initial finite element mesh of the half-space in the load application area in plan and along the depth is 0,25 m. The sizes of the finite elements increase with the distance from the load application area.
Internal forces are output along the axes of the global coordinate system. Upper faces of the elements of the half-space boundary are subjected to the surface transverse load within the following dimensions in plan 2a×2b = 4.0 м×4.0 m.
The boundary conditions were defined as follows: normal displacements on the lower and side surfaces are restrained.
Number of nodes in the design model – 573985.
Results in SCAD

Design model

Deformed model of the surface of the elastic half-space
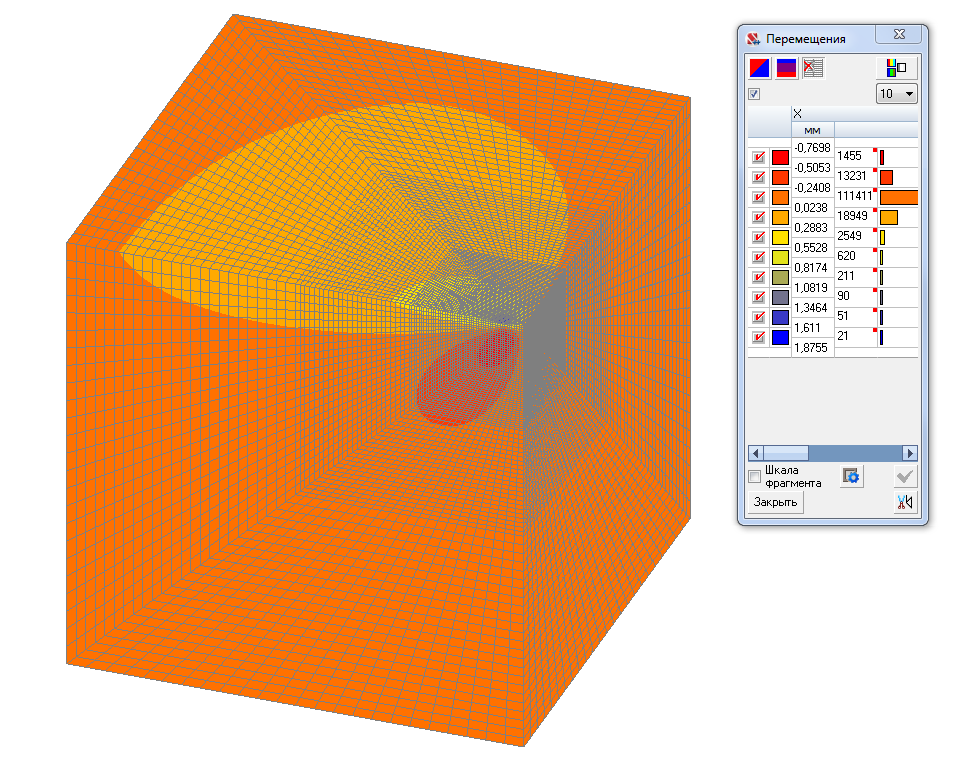
Values of horizontal displacements u (mm)
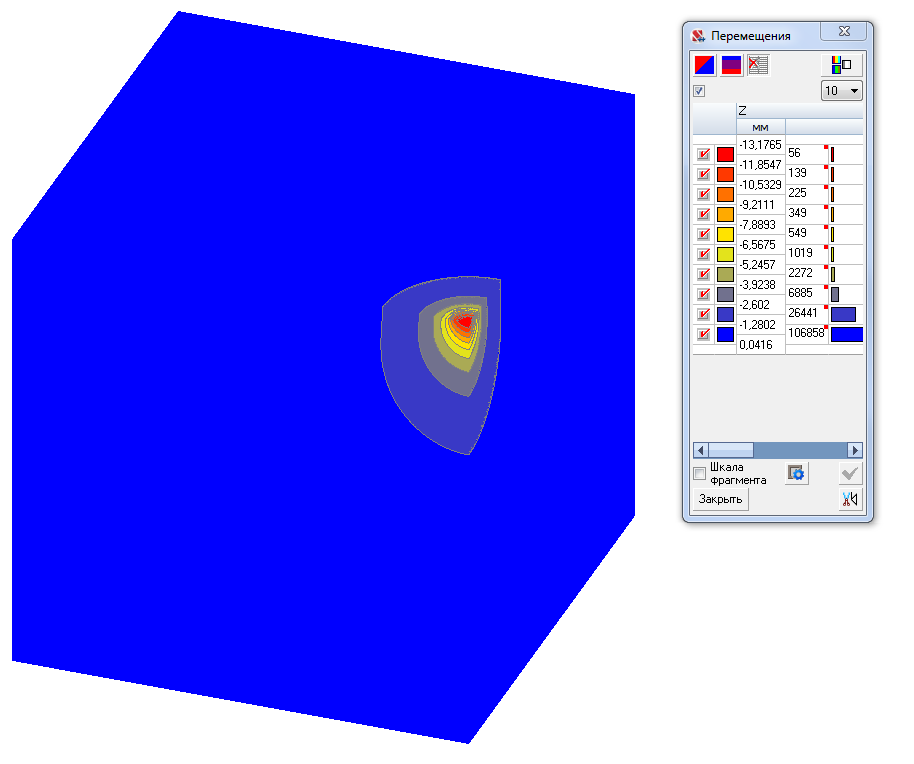
Values of vertical displacements w (mm)
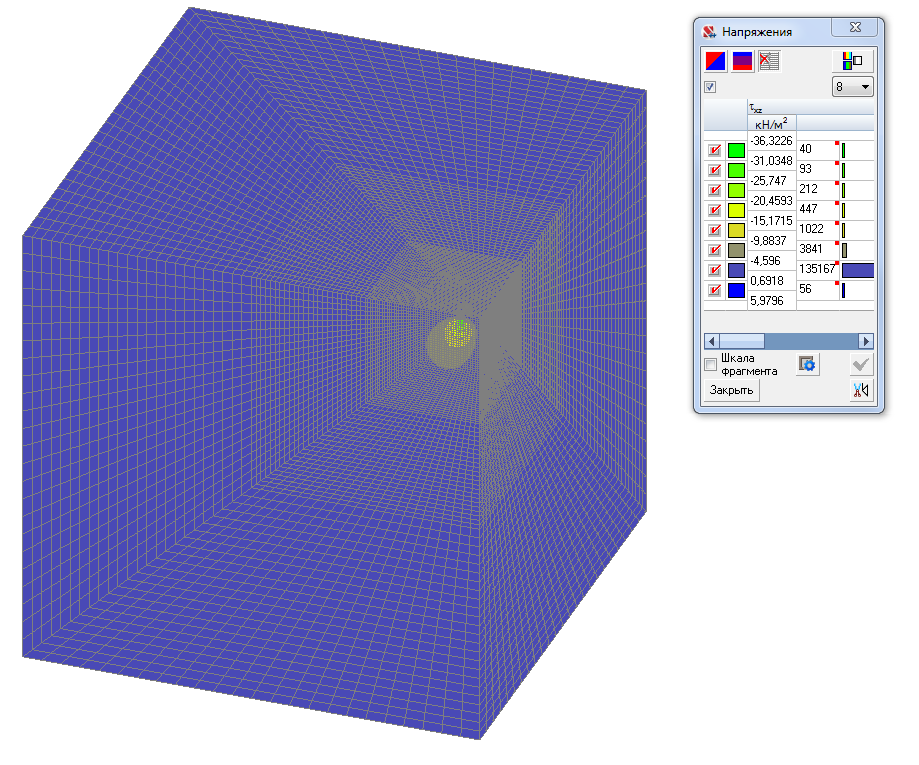
Values of vertical τxz tangential stresses (t/m2)
Comparison of solutions:
Solution of the Love’s problem by 20-node
isoparametric elements (mm, kN/m2)
|
Point |
Parameter |
|
Theory |
SCAD |
Deviations, % |
|---|---|---|---|---|---|
|
(0,0,0) Node 1 |
w |
mm |
-13,616 |
-13,177 |
3,2 |
|
σx=σy |
kN/m2 |
-80,0 |
-79,919 |
0,10 |
|
|
σz |
kN/m2 |
-100,0 |
-100,079 |
0,09 |
|
|
(0,0,-2) Node 10005 |
w |
mm |
-9,017 |
-8,574 |
4,91 |
|
σx=σy |
kN/m2 |
-8,29 |
-8,189 |
1,21 |
|
|
σz |
kN/m2 |
-70,09 |
-70,109 |
0,03 |
|
|
(-2,2,-2) Node 10213 |
u=v |
mm |
0,488 |
0,492 |
0,82 |
|
w |
mm |
-5,704 |
-5,262 |
7,75 |
|
|
σx=σy |
kN/m2 |
-7,56 |
-7,496 |
0,85 |
|
|
σz |
kN/m2 |
-23,25 |
-23,267 |
0,07 |
|
|
τxy |
kN/m2 |
-5,27 |
-5,288 |
0,34 |
|
|
τxz=τyz |
kN/m2 |
12,11 |
12,166 |
0,46 |
Notes: In the analytical solution the distribution of the normal stresses σx, σy, σz, tangential stresses τxy, τxz, τyz and displacements u, v, w across the half-space is determined according to the following formulas:
\[ \sigma_{x} (x,y,z)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\,(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{(x-a)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}-(y-b)^{2}+z^{2}} }} \right]} \right.+ \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{z\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x-a)\cdot (y-b)}{\left[ {(x-a)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{(x-a)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]- \] \[ -2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x-a)\cdot (y+b)}{\left[ {(x-a)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{(x+a)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]- \] \[ -2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x+a)\cdot (y-b)}{\left[ {(x+a)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }- \] \[ -(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{(x+a)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ \left. {+2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x+a)\cdot (y+b)}{\left[ {(x+a)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right\} . \] \[ \sigma_{y} (x,y,z)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\,(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{(y-b)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}-(y-b)^{2}+z^{2}} }} \right]} \right.+ \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x-a)\cdot (y-b)}{z\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x-a)\cdot (y-b)}{\left[ {(y-b)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y-b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x-a)\cdot (y+b)}{(y+b)^{2}+z^{2}-z\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ +\frac{z\cdot (x-a)\cdot (y+b)}{\left[ {(y+b)^{2}+z^{2}} \right]\cdot \sqrt {(x-a)^{2}+(y+b)^{2}+z^{2}} }+ \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{(y-b)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]- \] \[ +2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y-b)}{z\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }} \right]+\frac{z\cdot (x+a)\cdot (y-b)}{\left[ {(y-b)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y-b)^{2}+z^{2}} }- \] \[ +(1-2\cdot \mu )\cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{(y+b)^{2}+z^{2}-z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]+ \] \[ \left. {+2\cdot \mu \cdot arctg\left[ {\frac{(x+a)\cdot (y+b)}{z\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right]-\frac{z\cdot (x+a)\cdot (y+b)}{\left[ {(y+b)^{2}+z^{2}} \right]\cdot \sqrt {(x+a)^{2}+(y+b)^{2}+z^{2}} }} \right\} . \]
\[ {\sigma_{z} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {\frac{z\cdot \left( {x-a} \right)\cdot \left( {y-b} \right)\cdot \left[ {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y-b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} \right.} \\ {+arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} {-\frac{z\cdot \left( {x-a} \right)\cdot \left( {y+b} \right)\cdot \left[ {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y+b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }-} \\ {-arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} {-\frac{z\cdot \left( {x+a} \right)\cdot \left( {y-b} \right)\cdot \left[ {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y-b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \\ {-arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} {+\frac{z\cdot \left( {x+a} \right)\cdot \left( {y+b} \right)\cdot \left[ {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+2\cdot z^{2}} \right]}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \left[ {\left( {y+b} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} \\ {\left. {+arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \\ \]
\[ {\tau_{xy} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \right.} \\ {+\frac{z}{\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} {+\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\frac{z}{\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} {+\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\frac{z}{\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }-} {-\left( {1-2\cdot \mu } \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {\left. {+\frac{z}{\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right\} .} \]
\[ {\tau_{xz} \left( {x,y,z} \right)=\frac{q}{2\cdot \pi }\cdot \left\{ {-\frac{z^{2}\cdot \left( {y-b} \right)}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }+} \right.} \\ {+\frac{z^{2}\cdot \left( {y+b} \right)}{\left[ {\left( {x-a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }+} {+\frac{z^{2}\cdot \left( {y-b} \right)}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }-} \\ {\left. {-\frac{z^{2}\cdot \left( {y+b} \right)}{\left[ {\left( {x+a} \right)^{2}+z^{2}} \right]\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right\} .} \]
\[ {u\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]-} \right.} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left( {\frac{y-b}{x-a}} \right)-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y-b} \right)}{\left( {x-a} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left( {\frac{y+b}{x-a}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y+b} \right)}{\left( {x-a} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left( {\frac{y-b}{x+a}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y-b} \right)}{\left( {x+a} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left( {\frac{y+b}{x+a}} \right)-} \\ {\left. {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot arctg\left[ {\frac{z\cdot \left( {y+b} \right)}{\left( {x+a} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \\ \]
\[ {v\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]-} \right.} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left( {\frac{x-a}{y-b}} \right)-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x-a} \right)}{\left( {y-b} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left( {\frac{x-a}{y+b}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x-a} \right)}{\left( {y+b} \right)\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} -z} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left( {\frac{x+a}{y-b}} \right)+} \\ {+\left( {1-2\cdot \mu } \right)\cdot \left( {y-b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x+a} \right)}{\left( {y-b} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot z\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} -z} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left( {\frac{x+a}{y+b}} \right)-} \\ {\left. {-\left( {1-2\cdot \mu } \right)\cdot \left( {y+b} \right)\cdot arctg\left[ {\frac{z\cdot \left( {x+a} \right)}{\left( {y+b} \right)\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \]
\[ {w\left( {x,y,z} \right)=\frac{q\cdot \left( {1+\mu } \right)}{2\cdot \pi \cdot E}\cdot \left\{ {-2\cdot \left( {1-\mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]-} \right.} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]+} \\ {+\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {x-a} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x-a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x-a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x-a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {y-b} \right)} \right]+} \\ {+2\cdot \left( {1-\mu } \right)\cdot \left( {y-b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]-} \\ {-\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y-b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y-b} \right)^{2}+z^{2}} }} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {x+a} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {y+b} \right)} \right]-} \\ {-2\cdot \left( {1-\mu } \right)\cdot \left( {y+b} \right)\cdot ln\left[ {\sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} +\left( {x+a} \right)} \right]+} \\ {\left. {+\left( {1-2\cdot \mu } \right)\cdot z\cdot arctg\left[ {\frac{\left( {x+a} \right)\cdot \left( {y+b} \right)}{z\cdot \sqrt {\left( {x+a} \right)^{2}+\left( {y+b} \right)^{2}+z^{2}} }} \right]} \right\} .} \]
