Response Spectrum of Absolute Response Accelerations of a Linear Oscillator Installed in the Middle of the Span of a Simply Supported Beam with a Distributed Mass Subjected to a Kinematic Excitation of Supports (Seismic Action)
Objective: Determination of the response spectrum of response accelerations of a linear oscillator installed in the middle of the span of a simply supported beam with a distributed mass subjected to a kinematic excitation of supports.
Initial data files:
DIN_B_RS.SPR – design model
DIN_B_RS.SPC – accelerogram
Problem formulation: The simply supported beam of constant cross-section with the uniformly distributed mass μ is subjected to the kinematic excitation of the supports according to the specified accelerogram:
\[ \ddot{{z}}(t)=\ddot{{z}}_{s0} \cdot \left( {1-\frac{t}{t_{d} }} \right). \]
Determine the response spectrum of the absolute response accelerations of the linear oscillator installed in the middle of the span.
References: John M. Biggs, Introduction to Structural Dynamics, McGraw-Hill Book Companies, New York, 1964, p.256-263;
Kiselev V.A., Structural Mechanics. Special Course. Dynamics and Stability of Structures. Moscow, Stroyizdat, 1980, p. 65-67.
Initial data:
| E = 3.0·107 psi = 2.1092·107 tf/m2 | - elastic modulus; |
| I = 333.333 in4 = 138.7448·10-6 m4 | - cross-sectional moment of inertia of the beam. |
| h = 14 in = 0.3556 m | - height of the cross-section of the beam; |
| L = 240 in = 6.0960 m | - beam span length; |
| μ = 0.2 lb·sec2/in2 = 0.1406 tf·s2/m2 | - value of the uniformly distributed mass of the beam; |
| \( \ddot{{z}}_{s0} \) = ±386.2200 in/sec2 = ±9.81 m/s2 | - amplitude values of the acceleration of the supports according to the accelerogram; |
| td = 0.10 sec = 0.10 s | - half-interval of the kinematic excitation of supports; |
| g = 386.2200 in/sec2 =9.81 m/s2 | - gravitational acceleration; |
Finite element model: Design model – grade beam / plate, 32 bar elements of type 3. Boundary conditions of the simply supported ends of the beam are provided by imposing constraints in the direction of the degree of freedom Z. The dimensional stability of the design model is provided by imposing a constraint in the node of the cross-section along the symmetry axis of the beam in the direction of the degree of freedom UX. The distributed mass is specified by transforming the static load from the self-weight of the beam μ·g.
The kinematic excitation of supports is described by the graph of the acceleration variation with time (accelerogram) and is given in the form of the action along the Z axis of the global coordinate system (direction cosines to the X, Y, Z axes: 0.00, 0.00, 1.00) with the scale factor to the values of the accelerogram equal to 1.00. The height of the beam structure in the model is directed along the Z axis of the global coordinate system. The dissipation factor (energy absorption factor) is taken with the minimum value ξ = 0.000001 for the oscillator and for the structure. The intervals between the time points of the graph of the acceleration variation with time are equal to Δt = 0.01 s. When plotting the graph the acceleration is taken with the values \( \ddot{{z}}(t)=\ddot{{z}}_{s0} \cdot \left( {1-n \cdot \Delta t} / {t_{d} } \right). \) at the time points n·Δt. The conversion factor for the added static loading is equal to k = 1.000 (mass generation). Number of nodes in the design model – 33.
Results in SCAD
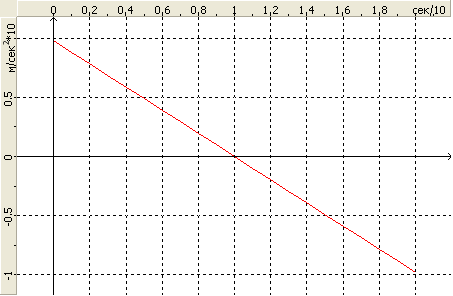
Design model and the given accelerogram
Comparison of solutions:
The comparison was performed with the solution of the problem obtained in Abaqus (the solution was provided by A.I. Popov — Atomproekt).
|
Frequency |
Acceleration |
|
|---|---|---|
|
Hz |
g |
|
|
Abaqus |
SCAD |
|
|
0 |
0,0000 |
0,0000 |
|
0,05 |
0,0000 |
0,0007 |
|
0,1 |
0,0000 |
0,0029 |
|
0,15 |
0,0000 |
0,0064 |
|
0,2 |
0,0000 |
0,0114 |
|
0,25 |
0,0038 |
0,0178 |
|
0,3 |
0,0027 |
0,0256 |
|
0,35 |
0,0216 |
0,0347 |
|
0,4 |
0,0200 |
0,0452 |
|
0,45 |
0,0490 |
0,0569 |
|
0,5 |
0,0503 |
0,0700 |
|
0,55 |
0,0832 |
0,0842 |
|
0,6 |
0,0881 |
0,0997 |
|
0,65 |
0,1218 |
0,1163 |
|
0,7 |
0,1312 |
0,1340 |
|
0,75 |
0,1642 |
0,1528 |
|
0,8 |
0,1799 |
0,1726 |
|
0,85 |
0,2096 |
0,1934 |
|
0,9 |
0,2310 |
0,2152 |
|
0,95 |
0,2565 |
0,2378 |
|
1 |
0,2824 |
0,2613 |
|
1,05 |
0,3045 |
0,2855 |
|
1,1 |
0,3338 |
0,3105 |
|
1,15 |
0,3625 |
0,3362 |
|
1,2 |
0,3876 |
0,3626 |
|
1,25 |
0,4182 |
0,3895 |
|
1,3 |
0,4481 |
0,4171 |
|
1,35 |
0,4758 |
0,4453 |
|
1,4 |
0,5043 |
0,4739 |
|
1,45 |
0,5395 |
0,5030 |
|
1,5 |
0,5690 |
0,5325 |
|
1,55 |
0,5964 |
0,5625 |
|
1,6 |
0,6324 |
0,5928 |
|
1,65 |
0,6656 |
0,6235 |
|
1,7 |
0,6953 |
0,6545 |
|
1,75 |
0,7270 |
0,6857 |
|
1,8 |
0,7628 |
0,7171 |
|
1,85 |
0,7932 |
0,7487 |
|
1,9 |
0,8267 |
0,7804 |
|
1,95 |
0,8572 |
0,8121 |
|
2 |
0,8939 |
0,8441 |
|
2,05 |
0,9265 |
0,8760 |
|
2,1 |
0,9559 |
0,9079 |
|
2,15 |
0,9913 |
0,9398 |
|
2,2 |
1,0234 |
0,9717 |
|
2,25 |
1,0561 |
1,0035 |
|
2,3 |
1,0887 |
1,0353 |
|
2,35 |
1,1193 |
1,0669 |
|
2,4 |
1,1498 |
1,0984 |
|
2,45 |
1,1855 |
1,1298 |
|
2,5 |
1,2171 |
1,1611 |
|
2,55 |
1,2467 |
1,1923 |
|
2,6 |
1,2762 |
1,2234 |
|
2,65 |
1,3048 |
1,2544 |
|
2,7 |
1,3405 |
1,2853 |
|
2,75 |
1,3721 |
1,3160 |
|
2,8 |
1,4027 |
1,3465 |
|
2,85 |
1,4312 |
1,3769 |
|
2,9 |
1,4597 |
1,4071 |
|
2,95 |
1,4862 |
1,4370 |
|
3 |
1,5158 |
1,4667 |
|
3,05 |
1,5454 |
1,4963 |
|
3,1 |
1,5749 |
1,5255 |
|
3,15 |
1,6045 |
1,5546 |
|
3,2 |
1,6320 |
1,5832 |
|
3,25 |
1,6595 |
1,6115 |
|
3,3 |
1,6860 |
1,6395 |
|
3,35 |
1,7115 |
1,6671 |
|
3,4 |
1,7370 |
1,6943 |
|
3,45 |
1,7604 |
1,7211 |
|
3,5 |
1,7829 |
1,7476 |
|
3,55 |
1,8084 |
1,7736 |
|
3,6 |
1,8318 |
1,7994 |
|
3,65 |
1,8583 |
1,8247 |
|
3,7 |
1,8838 |
1,8499 |
|
3,75 |
1,9093 |
1,8744 |
|
3,8 |
1,9337 |
1,8989 |
|
3,85 |
1,9541 |
1,9226 |
|
3,9 |
1,9776 |
1,9629 |
|
3,95 |
2,0000 |
2,0807 |
|
4 |
2,0224 |
2,1999 |
|
4,05 |
2,0438 |
2,3202 |
|
4,1 |
2,1244 |
2,4415 |
|
4,15 |
2,1713 |
2,5635 |
|
4,2 |
2,2895 |
2,6862 |
|
4,25 |
2,4088 |
2,8092 |
|
4,3 |
2,5291 |
2,9324 |
|
4,35 |
2,6493 |
3,0555 |
|
4,4 |
2,7696 |
3,1784 |
|
4,45 |
2,8899 |
3,3009 |
|
4,5 |
2,7768 |
3,4226 |
|
4,55 |
2,8960 |
3,5434 |
|
4,6 |
3,0143 |
3,6631 |
|
4,65 |
3,1325 |
3,7815 |
|
4,7 |
3,2497 |
3,8982 |
|
4,75 |
3,3660 |
4,0132 |
|
4,8 |
3,4811 |
4,1262 |
|
4,85 |
3,5953 |
4,2370 |
|
4,9 |
3,8267 |
4,3453 |
|
4,95 |
3,9368 |
4,4509 |
|
5 |
4,0449 |
4,5537 |
|
5,05 |
4,1519 |
4,6535 |
|
5,15 |
4,3568 |
4,8429 |
|
5,25 |
4,5515 |
5,0178 |
|
5,35 |
4,7339 |
5,1765 |
|
5,45 |
5,1580 |
5,3179 |
|
5,55 |
5,2915 |
5,4406 |
|
5,65 |
5,4057 |
5,5436 |
|
5,75 |
5,5025 |
5,6259 |
|
5,85 |
5,5800 |
5,6867 |
|
5,95 |
5,6371 |
5,7255 |
|
6,05 |
5,6799 |
5,7418 |
|
6,15 |
5,6922 |
5,7467 |
|
6,25 |
5,6840 |
5,7459 |
|
6,35 |
5,6667 |
5,7410 |
|
6,45 |
5,6616 |
5,7305 |
|
6,55 |
5,6381 |
5,7172 |
|
6,65 |
5,6106 |
5,7002 |
|
6,75 |
5,5933 |
5,6823 |
|
6,85 |
5,5596 |
5,6593 |
|
6,95 |
5,5260 |
5,6326 |
|
7,05 |
5,4760 |
5,6019 |
|
7,15 |
5,4475 |
5,5663 |
|
7,25 |
5,4027 |
5,5263 |
|
7,35 |
5,3435 |
5,4817 |
|
7,45 |
5,3058 |
5,4330 |
|
7,55 |
5,2548 |
5,3803 |
|
7,65 |
5,1906 |
5,3244 |
|
7,75 |
5,1366 |
5,2659 |
|
7,85 |
5,0856 |
5,2063 |
|
7,95 |
5,0214 |
5,1456 |
|
8,05 |
4,9541 |
5,0832 |
|
8,15 |
4,8970 |
5,0199 |
|
8,25 |
4,8298 |
4,9568 |
|
8,35 |
4,7533 |
4,8934 |
|
8,45 |
4,6942 |
4,8276 |
|
8,55 |
4,6259 |
4,7590 |
|
8,65 |
4,5484 |
4,6880 |
|
8,75 |
4,4791 |
4,6150 |
|
8,85 |
4,4108 |
4,5400 |
|
8,95 |
4,3354 |
4,4637 |
|
9,05 |
4,2538 |
4,3856 |
|
9,15 |
4,1876 |
4,3056 |
|
9,25 |
4,1121 |
4,2230 |
|
9,35 |
4,0306 |
4,1386 |
|
9,45 |
3,9602 |
4,0539 |
|
9,55 |
3,8858 |
3,9697 |
|
9,65 |
3,8063 |
3,8864 |
|
9,75 |
3,7278 |
3,8045 |
|
9,85 |
3,6565 |
3,7235 |
|
9,95 |
3,5800 |
3,6425 |
|
10,05 |
3,5005 |
3,5625 |
|
10,25 |
3,3517 |
3,4065 |
|
10,45 |
3,1978 |
3,2517 |
|
10,65 |
3,0510 |
3,0950 |
|
10,85 |
2,9021 |
2,9342 |
|
11,05 |
2,7554 |
2,8493 |
|
11,25 |
2,6320 |
2,8338 |
|
11,45 |
2,6188 |
2,8165 |
|
11,65 |
2,6045 |
2,7987 |
|
11,85 |
2,5851 |
2,7780 |
|
12,05 |
2,5668 |
2,7555 |
|
12,25 |
2,5525 |
2,7311 |
|
12,45 |
2,5352 |
2,7038 |
|
12,65 |
2,5138 |
2,6768 |
|
12,85 |
2,4954 |
2,6496 |
|
13,05 |
2,4791 |
2,6235 |
|
13,25 |
2,4608 |
2,6008 |
|
13,45 |
2,4393 |
2,5794 |
|
13,65 |
2,4190 |
2,5580 |
|
13,85 |
2,4200 |
2,5829 |
|
14,05 |
2,4669 |
2,6253 |
|
14,25 |
2,5025 |
2,6754 |
|
14,45 |
2,5321 |
2,7204 |
|
14,65 |
2,5545 |
2,7508 |
|
14,85 |
2,5668 |
2,7680 |
|
15,05 |
2,5770 |
2,7730 |
|
15,25 |
2,5780 |
2,7656 |
|
15,45 |
2,5708 |
2,7468 |
|
15,65 |
2,5627 |
2,7165 |
|
15,85 |
2,5433 |
2,6732 |
|
16,05 |
2,5270 |
2,6209 |
|
16,25 |
2,4995 |
2,5750 |
|
16,45 |
2,4730 |
2,5384 |
|
16,65 |
2,4383 |
2,5071 |
|
16,85 |
2,4037 |
2,4806 |
|
17,05 |
2,3629 |
2,4496 |
|
17,25 |
2,3221 |
2,4087 |
|
17,45 |
2,2742 |
2,3604 |
|
17,65 |
2,2294 |
2,3022 |
|
17,85 |
2,1774 |
2,2363 |
|
18,05 |
2,1284 |
2,1646 |
|
18,25 |
2,0724 |
2,0879 |
|
18,45 |
2,0204 |
2,0594 |
|
18,65 |
1,9602 |
2,1352 |
|
18,85 |
1,9215 |
2,1977 |
|
19,05 |
1,9541 |
2,2423 |
|
19,25 |
2,0071 |
2,2704 |
|
19,45 |
2,0530 |
2,2876 |
|
19,65 |
2,0968 |
2,2987 |
|
19,85 |
2,1356 |
2,3222 |
|
20,05 |
2,1672 |
2,3682 |
|
20,55 |
2,2365 |
2,5018 |
|
21,05 |
2,2783 |
2,5673 |
|
21,55 |
2,3028 |
2,5700 |
|
22,05 |
2,3007 |
2,5106 |
|
22,55 |
2,2854 |
2,3830 |
|
23,05 |
2,2528 |
2,3421 |
|
23,55 |
2,2039 |
2,3615 |
|
24,05 |
2,1427 |
2,3313 |
|
24,55 |
2,0734 |
2,2381 |
|
25,05 |
1,9949 |
2,2560 |
|
25,55 |
1,9888 |
2,2237 |
|
26,05 |
2,0601 |
2,3334 |
|
26,55 |
2,1142 |
2,4863 |
|
27,05 |
2,1580 |
2,5792 |
|
27,55 |
2,1865 |
2,6055 |
|
28,05 |
2,1988 |
2,5678 |
|
28,55 |
2,1978 |
2,4566 |
|
29,05 |
2,1876 |
2,2866 |
|
29,55 |
2,1702 |
2,3166 |
|
30,05 |
2,1386 |
2,4101 |
|
30,55 |
2,0989 |
2,4521 |
|
31,05 |
2,0520 |
2,4243 |
|
31,55 |
1,9980 |
2,3600 |
|
32,05 |
2,0071 |
2,3904 |
|
32,55 |
2,0520 |
2,5854 |
|
33,05 |
2,0907 |
2,7152 |
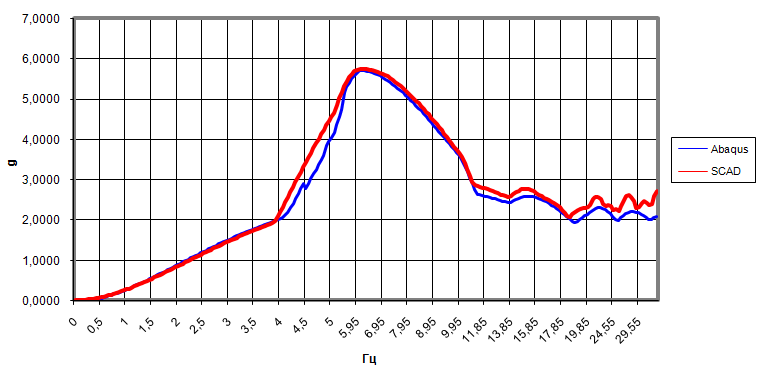
Response Spectra
|
|
Abaqus |
SCAD |
Deviation |
|---|---|---|---|
|
Frequency at which the maximum acceleration occurs (Hz) |
6.15 |
6.15 |
0 % |
|
Maximum acceleration (g) |
5,6921 |
5.7467 |
0.95 % |
|
Spectra correlation coefficient |
0.995 |
||