Seismic Response of a Beam according to the Linear Spectral Theory
Objective: The linear spectral method (determination of the response of a structure subjected to the seismic action given by the accelerogram)
Initial data files:
LinSpectral.SPR – design model
DIN_B_RS.SPC – accelerogram
Problem formulation: The simply supported beam of constant cross-section with the uniformly distributed mass μ is subjected to the kinematic excitation of supports according to the specified accelerogram:
\[ \ddot{{z}}(t)=\ddot{{z}}_{s0} \cdot \left( {1-\frac{t}{t_{d} }} \right) \]
It is necessary to determine (by the LST) seismic displacements and the corresponding maximum bending stress.
References: John M. Biggs, Introduction to Structural Dynamics, McGraw-Hill Book Companies, New York, 1964, p.262;
Initial data:
| E = 3.0·107 psi = 2.1092·107 tf/m2 | - elastic modulus; |
| I = 333.333 in4 = 138.7448·10-6 m4 | - cross-sectional moment of inertia of the beam. |
| h = 14 in = 0.3556 m | - height of the cross-section of the beam; |
| L = 240 in = 6.0960 m | - beam span length; |
| μ = 0.2 lb·sec2/in2 = 0.1406 tf·s2/m2 | - value of the uniformly distributed mass of the beam; |
| \( \ddot{{z}}(t) \)= ±386.2200 in/sec2 = ±9.81 m/s2 | - amplitude values of the acceleration of the supports according to the accelerogram; |
| tю = 0.10 sec = 0.10 с | - half-interval of the kinematic excitation of supports; |
| g = 386.2200 in/sec2 =9.81 м/с2 | - gravitational acceleration; |

Finite element model: Design model – 32 bar elements of type 3. Boundary conditions of the simply supported ends of the beam are provided by imposing constraints in the direction of the degree of freedom Z. The dimensional stability of the design model is provided by imposing a constraint in the node of the cross-section along the symmetry axis of the beam in the direction of the degree of freedom UX. The distributed mass is specified by transforming the static load from the self-weight of the beam μ·g.
The kinematic excitation of supports is described by the graph of the acceleration variation with time (accelerogram) and is given in the form of the action along the Z axis of the global coordinate system (direction cosines to the X, Y, Z axes: 0.00, 0.00, 1.00) with the scale factor to the values of the accelerogram equal to 1.00. The height of the beam structure in the model is directed along the Z axis of the global coordinate system. The dissipation factor is taken as ξ = 0.000001. The intervals between the time points of the graph of the acceleration variation with time are equal to Δt = 0.01 s. When plotting the graph the acceleration is taken with the values \( \ddot{z}(t)=\ddot{z}_{s0} \cdot \left( {1-n \cdot \Delta t / t_{d}} \right) \) at the time points n·Δt. The conversion factor for the added static loading is equal to k = 1.000 (mass generation). Number of nodes in the design model – 33. The determination of the natural oscillation modes and natural frequencies is performed by the method of subspace iteration. The matrix of concentrated masses is used in the calculation.
Results in SCAD
The 1-st natural frequency and the 1-st natural oscillation mode of the beam, seismic bending stresses on the bottom face of the beam and displacements are determined in the result of the calculation.

Design and deformed models
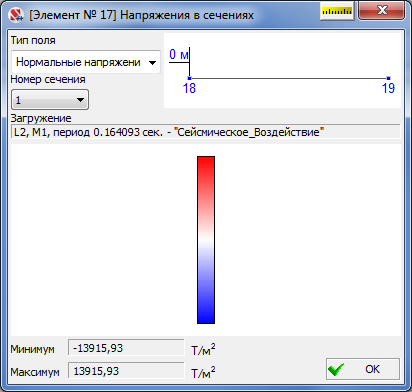
Normal stresses in the middle of the span
Comparison of solutions:
|
|
Source |
SCAD |
Deviation |
|---|---|---|---|
|
1-st natural frequency (Hz) |
6,0979 |
6.0941 |
0,06 % |
|
Displacement of the beam in the middle of the span (m) |
0,01422 |
0,01397 |
1.75 % |
|
Maximum normal stress (T/m2) |
14172,70 |
13915,93 |
1.85 % |
