Doubly Clamped Beam Subjected to the Transverse Displacement of One of its Ends

Objective: Determination of the stress state of a doubly clamped beam subjected to the transverse displacement of one of its ends.

Initial data file: CS09_v11.3.spr

Problem formulation: The doubly clamped beam of a rectangular cross-section is subjected to a transverse displacement v of one of its ends. Determine the shear force Q and the bending moment M at the displaced end.

References: J. M. Gere and W. Weaver, Jr., Analysis of Framed Structures, New York, D. Van Nostrand Co., 1965.

Initial data:

E = 3.0·107 Pa	- elastic modulus,
L = 80.0 m	- beam length;
b = 2.0 m	- width of the beam cross-section;
h = 2.0 m	- height of the beam cross-section;
v = 1.0 m	- value of the transverse displacement.

 

Finite element model: Design model – plane frame, 4 elements of type 2. The spacing of the finite element mesh along the longitudinal axis (along the X axis of the global coordinate system) is 20.0 m. Boundary conditions at the clamped ends are provided by imposing constraints in the directions of the degrees of freedom: X, Z, UY. The action of the given transverse displacement is specified by the displacement of the respective constraint along the Z axis of the global coordinate system. Number of nodes in the design model – 5.

Results in SCAD

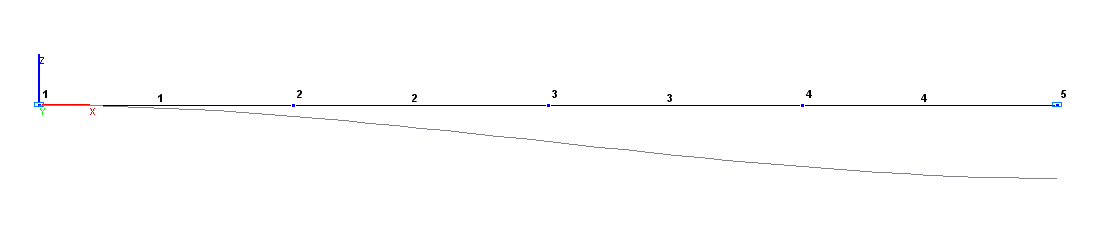
Design and deformed models

Shear force diagram Q (N)

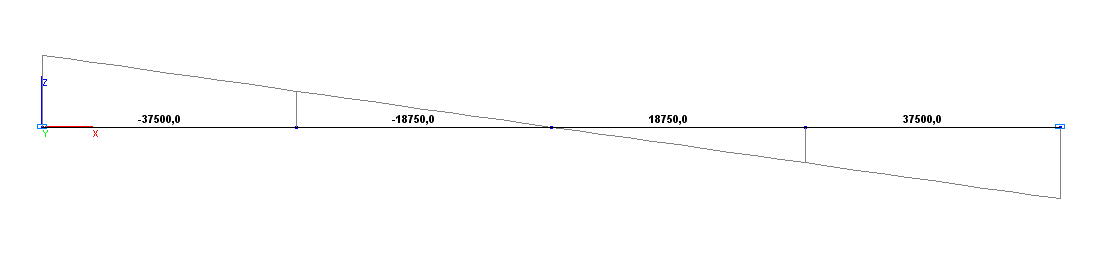
Bending moment diagram М (N∙m)

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Shear force Q at the displaced end, N	937.5	937.5	0.00
Bending moment M at the displaced end, N∙m	37500.0	37500.0	0.00

Notes: In the analytical solution, the shear force Q and the bending moment M at the displaced end are determined according to the following formulas:

\[ Q=\frac{12\cdot E\cdot I}{L^{3}}; \quad M=\frac{6\cdot E\cdot I}{L^{2}}, where: I=\frac{b\cdot h^{3}}{12}. \]