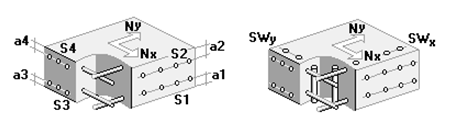
Example of Punching Near the Edge of the Slab

1 – closed design contour No.1, 2 – open design contour No.2, 3 – open design contour No.3.

Punching Analysis of a Flat Monolithic Floor Slab

Objective: Check the Punching mode in the “Reinforced Concrete” postprocessor of SCAD

Task: Verify the correctness of the punching strength analysis of a concrete element under a concentrated force and a bending moment when the load application area is near the edge of the slab.

Compliance with the codes: SNiP 52-101-2003, SP 63.13330.2012.

Initial data file:
SCAD 41 SP-2003.spr,
SCAD 41 SP-2012.spr 
report – SCAD 41 SP-2003.doc
report – SCAD 41 SP-2012.doc

Initial data:

 

 

 

h = 230 mm	Slab thickness
h0 = 200 mm	Average effective height of the slab
a×b = 500×400 mm	Column section sizes
F = 150 кН	Load transferred from the floor slab to the column
Msup = 80 kN∙m	Moment in the column section on the upper face of the slab
Minf = 90 kN∙m	Moment in the column section on the lower face of the slab
x0 = 500 mm	Distance from the center of the column section to the free edge of the slab
Concrete class	В25

 

Analytical solution:

In this case it is necessary to check the strength of three contours of the design cross-section:

contour No.1 – closed contour around the column section at a distance of 0,5h₀ from the column contour;

contour No.2 – open contour around the column section at a distance of 0,5h₀ from the column contour with the extension of the contour to the free edge of the slab;

contour No.3 – open contour around the column section at a distance of 0,5h₀ from the column contour (contour of the verification analysis without the consideration of the reinforcement).

1. Closed contour No.1:

L_x = A_x + h₀ = 500 + 200 = 700 мм = 0,7 м,

L_y = A_y + h₀ = 400 + 200 = 600 мм = 0,6 м,

Perimeter of the design contour of the cross-section:

u = 2(L_x + L_y) = 2 (0,7 + 0,6) = 2,6 м.

Area of the design contour of the cross-section:

A_b = uh₀ = 2,6 х 0,2 = 0,52 м².

Ultimate force resisted by concrete:

F_b,ult = R_btA_b = 1,05 х10³ х 0,52 = 546 kN.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =2\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad 2\frac{0,6^{3} }{12}+2\cdot 0,7\left( {\frac{0,6}{2}} \right)^{2}=\quad 0,162 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }== \quad \frac{0,162}{0,3}=\quad 0,54 м^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2\cdot L_{y} \left( {\frac{L_{x} }{2}} \right)^{2}= \quad 2\frac{0,7^{3} }{12}+2\cdot 0,6\left( {\frac{0,7}{2}} \right)^{2}=\quad 0,204 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{by} =\frac{I_{by} }{x_{\max } }== \quad \frac{0,204}{0,35}=\quad 0,583 м^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult = R_btW_bxh₀ = 1,05 х10³ х 1,217 х 0,2 = 255,57 кНм.

M_by,ult = R_btW_byh₀ = 1,05 х10³ х 0,547 х 0,2 = 114,87 кНм.

M_y = M_y - Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 кНм.

 

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{55,85}{114,87}=0,486\le \frac{F}{F_{b,ult} }=\frac{150}{651}=0,23 \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,275 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \]

\[ К1 = 0,275 + 0 + 0,275 = 0,55 \]

 

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} } + \frac{M_{y} }{M_{by,ult} } \le 0,5 \frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{85}{122,4}=0,694\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{546}=0,5\cdot 0,275=0,1375\quad \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,1375 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ К1 = 0,275 + 0 + 0,1375 = 0,413 \]

 

Open contour No.2:

L_x =A_x +h₀ + 150 = 500 + 200 + 150 = 850 mm = 0,85 m,

L_y =A_y +h₀  = 400 + 200 = 600 mm = 0,6 m,

Perimeter of the design contour of the cross-section:

u = 2L_x + L_y = 2х0,85 + 0,6 = 2,3 m.

Area of the design contour of the cross-section:

_Ab = uh₀ = 2,3 х 0,2 = 0,46 m².

X coordinate of the center of gravity of the open contour with respect to the left edge of the slab:

\[ X=\frac{425\cdot 850\cdot 2+850\cdot 600}{850\cdot 2+600}=535,869 мм \]

Ultimate force resisted by concrete:

F_b,ult = R_btA_b = 1,05 х103 х 0,46 = 483 kN.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad \frac{0,6^{3} }{12}+2\cdot 0,85\left( {\frac{0,6}{2}} \right)^{2}=\quad 0,171 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }= \quad \frac{0,171}{0,3}=\quad 0,57 м^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,075+0,035869)^{2}+L_{y} \left( {0,35-0,035869} \right)^{2}= 2\frac{0,85^{3} }{12}+2\cdot 0,85(0,075+0,035869)^{2}+0,6\left( {0,35-0,035869} \right)^{2}=0,183 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{by} =\frac{I_{by} }{x_{\max } }= \quad \frac{0,183}{0,535869}=\quad 0,341 м^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult = R_btW_bxh₀ =1,05 х103 х 0,57 х 0,2 = 119,7 kNm.

M_by,ult = R_btW_byh₀ = 1,05 х103 х 0,341 х 0,2 = 71,6 kNm.

M_y = M_y - Fe₀ = 85 – 150х0,035869 = 85 – 5,38 = 79,62 kNm.

 

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le \frac{F}{F_{b,ult} }=\frac{150}{483}=0,311 \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,311 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ К1 = 0,311+0+0,311 = 0,622 \]

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 0,5\frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{483}=0,5\cdot 0,311=0,155 \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ К1 = 0,311 + 0 + 0,155 = 0,466 \]

Open contour No.3:

L_x = A_x + 1,5h₀ + 250 = 500 +1,5х200 + 250 = 1050 mm = 1,05 m,

L_y = A_y + 2·1,5h₀ = 400 + 2х1,5х200 = 1000 mm = 1,0 m,

Perimeter of the design contour of the cross-section:

u = 2L_x + L_y = 2х1,05 + 1,0 = 3,1 m.

Area of the design contour of the cross-section:

A_b = uh₀ = 3,1 х 0,2 = 0,62 m².

X coordinate of the center of gravity of the open contour with respect to the left edge of the slab:

\[ X=\frac{525\cdot 1050\cdot 2+1050\cdot 1000}{1050\cdot 2+1000}=694,355 мм \]

Ultimate force resisted by concrete:

F_b,ult = R_btA_b = 1,05 х103 х 0,62 = 651 kN.

Moment of inertia of the design contour with respect to the X axis passing through its center of gravity:

\[ I_{bx} =\frac{L_{y}^{3} }{12}+2L_{x} \left( {\frac{L_{y} }{2}} \right)^{2}= \quad \frac{1,05^{3} }{12}+2\cdot 1,05\left( {\frac{1,0}{2}} \right)^{2}=\quad 0,608 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{bx} =\frac{I_{bx} }{y_{\max } }= \quad \frac{0,608}{0,5}=\quad 1,217 м^{2}. \]

Moment of inertia of the design contour with respect to the Y axis passing through its center of gravity:

\[ I_{by} =2\frac{L_{x}^{3} }{12}+2L_{x} (0,194355-0,025)^{2}+L_{y} \left( {1,05-0,694355} \right)^{2}= 2\frac{1,05^{3} }{12}+2\cdot 1,05(0,194355-0,025)^{2}+1,0\left( {1,05-0,694355} \right)^{2}=0,38 м^{3}. \]

Section modulus of the design contour of concrete

\[ W_{by} =\frac{I_{by} }{x_{\max } }= \quad \frac{0,38}{0,694355}=\quad 0,547 м^{2}. \]

Bending moment which can be resisted by concrete in the design cross-section:

M_bx,ult = R_btW_bxh₀ = 1,05 х103 х 1,217 х 0,2 = 255,57 kNm.

M_by,ult = R_btW_byh₀ = 1,05 х103 х 0,547 х 0,2 = 114,87 kNm.

M_y = M_y - Fe₀ = 85 – 150х0,194355 = 85 – 29,15 = 55,85 kNm.

 

For SNiP 52-101-2003:

\[ \frac{M_{x} }{M_{bx,ult} }\le \frac{F}{F_{b,ult} }; \quad \frac{M_{y} }{M_{by,ult} }\le \frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le \frac{F}{F_{b,ult} }=\frac{150}{483}=0,311 \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,311 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ К1 = 0,311+0+0,311 = 0,622 \]

For SP 63.13330.2012:

\[ \frac{M_{x} }{M_{bx,ult} }+\frac{M_{y} }{M_{by,ult} }\le 0,5\frac{F}{F_{b,ult} } \] \( \frac{M_{y} }{M_{by,ult} }=\frac{79,62}{71,6}=1,112\le 0,5\frac{F}{F_{b,ult} }=\frac{150}{483}=0,5\cdot 0,311=0,155 \)  – condition is not met.

Assume

\[ \frac{M_{y} }{M_{by,ult} }=\frac{F}{F_{b,ult} }=0,155 \]

Punching strength of the slab:

\[ K1=\left[ {\frac{F}{F_{b,ult} }} \right.+\left. {\frac{M_{x} }{M_{bx,ult}  }+\frac{M_{y} }{M_{by,ult} }} \right]\le 1,0 \] \[ К1 = 0,23 + 0 + 0,115 = 0,345
\]

 

Results of the SCAD analysis:

Node No. 5

Importance factor γ_n = 1
Concrete
Concrete type: Heavy-weight
Concrete class: B25

Service factor for concrete
γb1	allowance for the sustained loads	1
γb2	allowance for the failure behavior	1
γb3	allowance for the vertical position during concreting	1
γb4	allowance for the freezing/thawing and negative temperatures	1

 

Distance to the c.o.g. of reinforcement
a1	a2	a3	a4
mm	mm	mm	mm
30	30	0	0

 

Results

Design case – edge column

Length of the upper base of the bearing pyramid - 1800 mm
Length of the lower base of the bearing pyramid - 2300 mm

 

Comparison of solutions (according to SNiP 52-101-2003)

Checked according to SNiP	Check	Utilization factor
Sec.6.2.49	Strength without the consideration of the reinforcement	0,62

Check	punching strength of an unclosed concrete element under a concentrated force and bending moments (including additional ones caused by the eccentric application of a force with respect to the punched contour) with their vectors along X,Y-axes (load application area is near the edge of the slab)
Analytical solution	0,622
SCAD	0,62
Deviation, %	0,1 %

 

Comparison of solutions (according to SP 63.13330.2012)

Checked according to SP	Check	Utilization factor
Sec.8.1.49	Strength without the consideration of the reinforcement	0,47

Check	punching strength of an unclosed concrete element under a concentrated force and bending moments (including additional ones caused by the eccentric application of a force with respect to the punched contour) with their vectors along X,Y-axes (load application area is near the edge of the slab)
Analytical solution	0,466
SCAD	0,47
Deviation, %	0,1 %