Non-uniform Damping. Return to the Static Equilibrium Position
Objective: check that once the load ceases to change with time (we will call this value the static load component), the mechanical system subjected to the short-term loads and under damping returns to the static equilibrium position corresponding to the static load component.

Cantilever beam with a local damper
Initial data files:
beam_local_damp_1.SPR - design model
FileTimeFile.txt - time function
Problem formulation:
The cantilever beam with a 0.2 × 0.5 m rectangular cross-section, length of a = 3 m, and the elastic modulus of E = 23053.5 MN/m2 is considered. The specific weight is γ = 0.0245 MN/m3. The beam is divided into 3 finite elements. The matrix of concentrated masses is used. The maximum value of the force P is 0.01 MN.
The load vs. time relationship is given in the figure:
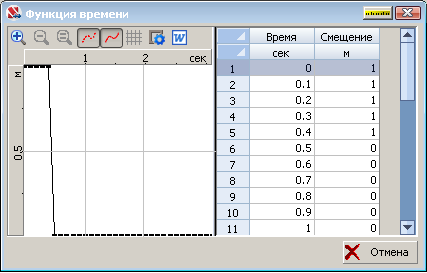
Finite element model: Design model – general type system, 6 general type bar elements (type 5) and one single-node damper (type 56). Number of nodes in the design model – 8. The matrix of concentrated masses is used in the calculation.
Results in SCAD
The vertical displacement of the cantilever end vs. time relationship at c = 0.01 MN∙s/m is given in the figure.
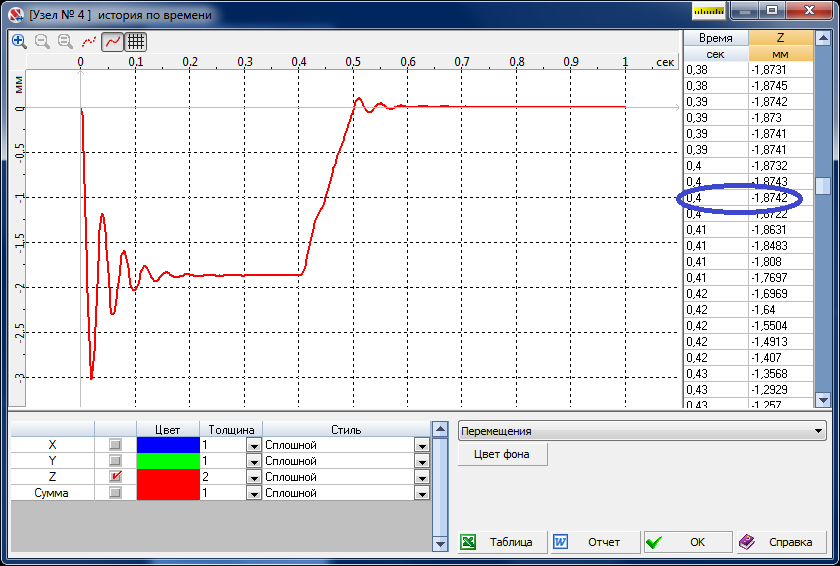
Vertical displacement of the cantilever end
Only the damping caused by the local damper is taken into account. When a load is suddenly applied, transverse oscillations of the beam appear and are rapidly damped. The value of the deflection corresponding to the state of static equilibrium at the force value of 0.01 MN is circled in the figure. The exact solution of the corresponding static problem is wst = Pa3/(3EI) = – 0.0018739 m. When the dynamic problem is solved by the Newmark method, the integration step is taken as 0.001 s. The result is accurate to 3 significant digits. This suggests that after the damping of oscillations we come to a static solution of this problem. At 0.4 s < t ≤ 0.5 s the load decreases to zero. Oscillations appear again and are rapidly damped. At t = 1 s the value of the normal deflection is w = –1.533∙10–7 m, which is a good approximation of zero, the exact value of the no-load static deflection, in comparison with the maximum (absolute value) deflection wmax = – 3.024∙10–3 m.
Thus, the numerical solution obtained by the Newmark method, after the damping of oscillations, converges to the static solution of this problem, which confirms the reliability of the obtained results.