Ring Subjected to a Distributed Load Acting in Its Plane
Objective: Analysis for bending in the ring plane under a concentrated force without taking into account the transverse shear deformations.
Initial data file: 4_7.spr
Problem formulation: The ring is subjected to a distributed load q acting in its plane. Determine: the normal force in the ring section N and the change in the ring diameter δ.
References: G.S. Pisarenko, A.P. Yakovlev, V.V. Matveev, Handbook on Strength of Materials. — Kiev: Naukova Dumka, 1988.
Initial data:
| E = 2.0·1011 Pa | - elastic modulus, |
| μ = 0.3 | - Poisson’s ratio, |
| R= 1 m | - ring radius; |
| F = 0,001 m2 | - cross-sectional area; |
| q = 100 kN/m | - value of the distributed load. |
Finite element model: Design model – general type system, 72 bar elements of type 10, 72 nodes.
Results in SCAD

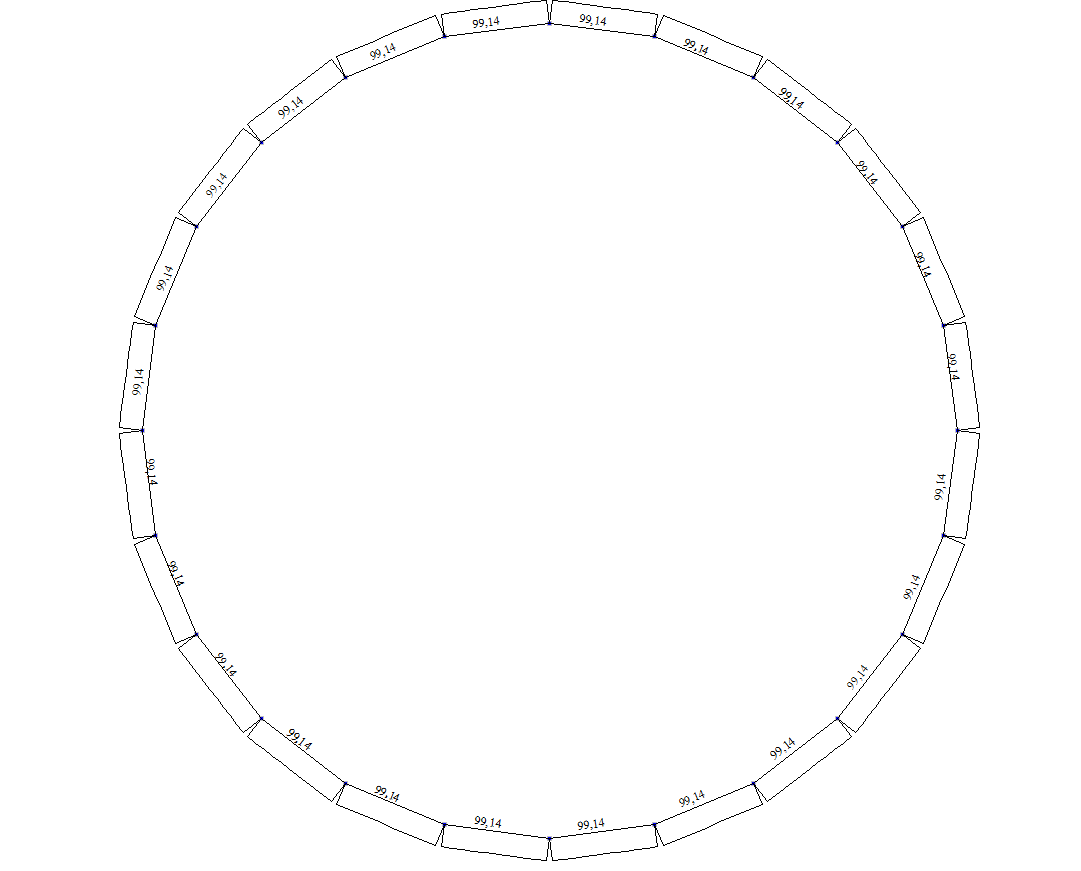
Normal force diagram N (kN)
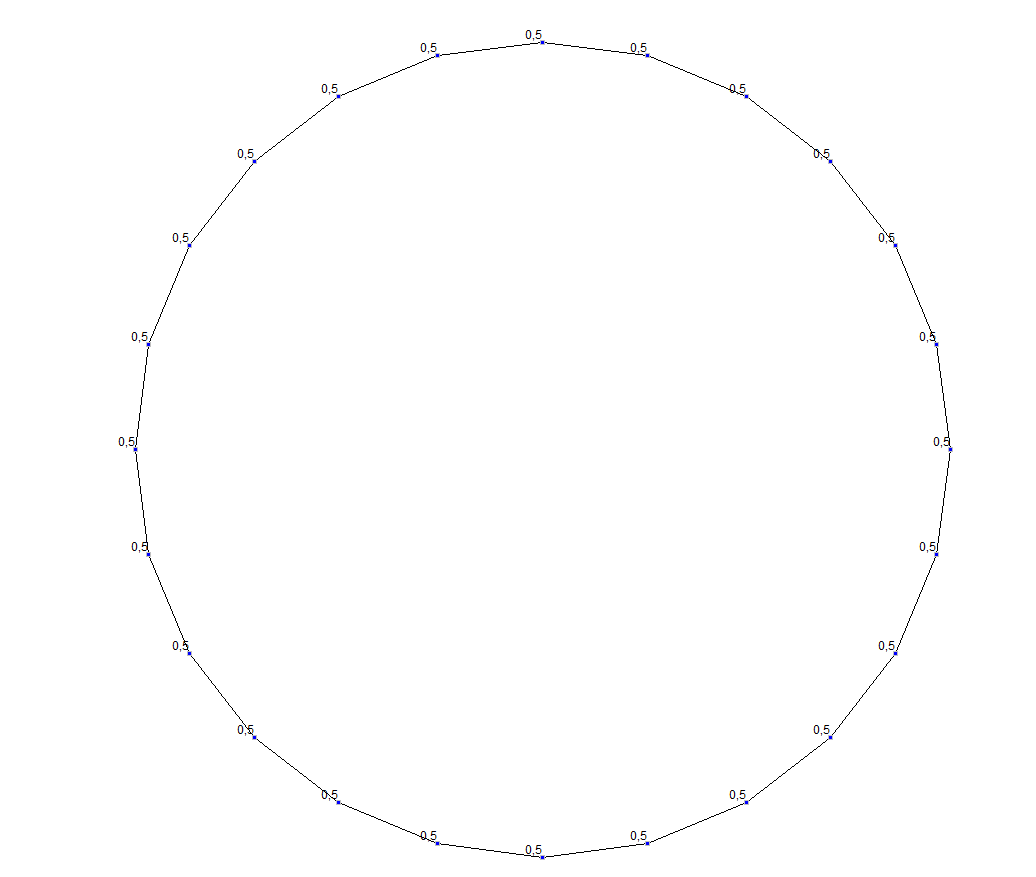
Values of displacements δ (mm)
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
Change in the ring diameter δ, mm |
0.50 |
0.50 |
0.00 |
|
Normal force in the ring section N, kN |
100.00 |
99.14 |
0.86 |
Notes: In the analytical solution, the change in the ring diameter is determined according to the following formulas (“Handbook on Strength of Materials” p. 384) :
\[ \delta_{x} =\delta_{y} =\frac{q\cdot R^{2}}{E\cdot F}. \]
Normal force in the ring section:
\[ N=q\cdot R. \]
