Bending of a Rectangular Deep Beam Rigidly Suspended along the Sides Subjected to a Uniformly Distributed Load Applied to Its Upper Side
Objective: Determination of the strain state of a rectangular deep beam rigidly suspended along the sides subjected to a uniformly distributed load applied to its upper side.
Initial data file: KSLS01_v11.3.spr
Problem formulation: The uniformly distributed load p acting in the plane of the deep beam along the y axis is applied to the upper side of the rectangular deep beam rigidly suspended along the sides. Determine the components of the strain tensor in the Cartesian coordinates u(x,z) and v(x,z) for the midsurface of the deep beam in its plane.
References: A.S. Kalmanok, Analysis of Deep Beams, Moscow, Gosstroyizdat, 1956.
Initial data:
| E = 2.65·106 Pa | - elastic modulus; |
| ν = 0.15 | - Poisson’s ratio; |
| h = 0.1 m | - thickness of the deep beam; |
| a = 1.6 m | - length of the deep beam span; |
| b = 1.6 m | - height of the deep beam; |
| p = 500.0 N/m | - uniformly distributed load. |
Finite element model: Design model – plane hinged bar system, 200 deep beam elements of type 21. The spacing of the finite element mesh along the x and z axes of the global coordinate system is 0.08 m. The boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z for the side and in the direction of the degree of freedom X at the symmetry axis. Number of nodes in the design model – 231.
Results in SCAD


Design model

Deformed model
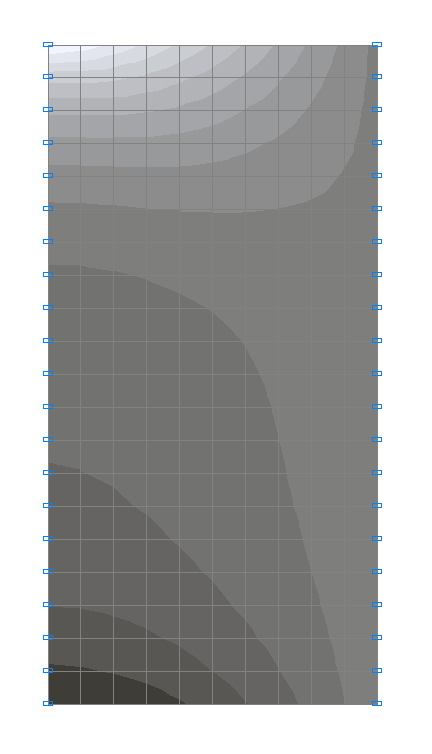

Values of displacements along the deep beam span u (m)
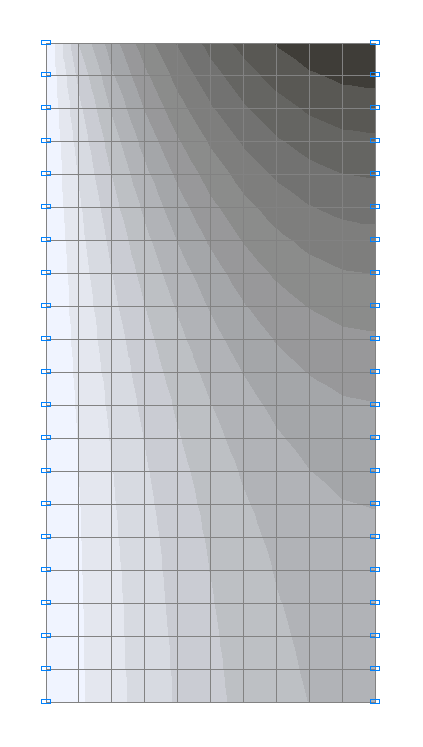

Values of displacements along the deep beam height v (m)
Comparison of solutions:
|
Coordinates |
Displacements u, m |
Displacements v, m |
|||||
|---|---|---|---|---|---|---|---|
|
x |
z |
Theory |
SCAD |
Deviations, % |
Theory |
SCAD |
Deviations, % |
|
0.0 |
0.0 |
-0.719∙10-3 |
-0.713∙10-3 |
0.83 |
0.000∙10-3 |
0.000∙10-3 |
─ |
|
0.0 |
0.8 |
-0.220∙10-3 |
-0.221∙10-3 |
0.45 |
0.000∙10-3 |
0.000∙10-3 |
─ |
|
0.0 |
1.6 |
1.468∙10-3 |
1.401∙10-3 |
4.56 |
0.000∙10-3 |
0.000∙10-3 |
─ |
|
0.4 |
0.0 |
-0.508∙10-3 |
-0.504∙10-3 |
0.79 |
-0.672∙10-3 |
-0.667∙10-3 |
0.74 |
|
0.4 |
0.8 |
-0.148∙10-3 |
-0.148∙10-3 |
0.00 |
-0.950∙10-3 |
-0.945∙10-3 |
0.53 |
|
0.4 |
1.6 |
0.780∙10-3 |
0.778∙10-3 |
0.26 |
-2.032∙10-3 |
-2.027∙10-3 |
0.25 |
|
0.8 |
0.0 |
0.000∙10-3 |
0.000∙10-3 |
─ |
-0.950∙10-3 |
-0.943∙10-3 |
0.74 |
|
0.8 |
0.8 |
0.000∙10-3 |
0.000∙10-3 |
─ |
-1.326∙10-3 |
-1.320∙10-3 |
0.45 |
|
0.8 |
1.6 |
0.000∙10-3 |
0.000∙10-3 |
─ |
-2.510∙10-3 |
-2.504∙10-3 |
0.24 |
Notes: In the analytical solution the components of the strain tensor in the Cartesian coordinates u(x,z) and v(x,z) for the midsurface of the deep beam in its plane can be calculated according to the following formulas:
\[
u\left( {x,z} \right)=-\frac{p\cdot b}{E\cdot h}\cdot
\sum\limits_{m=1}^{m=\infty } {\frac{a}{m\cdot \pi \cdot b}\cdot \left\{
{\left[ {2\cdot m\cdot \pi \cdot \frac{b}{a}\cdot sh\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right]\cdot \left[ {\left( {-2+\left( {1+\nu }
\right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi \cdot \frac{b-z}{a}}
\right)-} \right.} \right.}
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b-z}{a}\cdot
ch\left( {m\cdot \pi \cdot \frac{b-z}{a}} \right)} \right]-\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)+\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {-2+\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)} \right.-
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{z}{a}\cdot
ch\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]-\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)-\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {2\cdot \nu
+\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)} \right)\cdot sh\left( {m\cdot \pi
\cdot \frac{z}{a}} \right)-} \right.
\]
\[
\left. {\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot
\frac{z}{a}\cdot ch\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]}
\right\} \cdot \frac{\left[ {1+\left( {-1} \right)^{m+1}} \right]\cdot
cos\left( {m\cdot \pi \cdot \frac{x}{a}} \right)}{m\cdot \pi \cdot sh\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)\cdot \left[ {sh^{2}\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)-\left( {m\cdot \pi \cdot \frac{b}{a}}
\right)^{2}} \right]};
\]
\[
v\left( {x,z} \right)=\frac{p\cdot b}{E\cdot h}\cdot
\sum\limits_{m=1}^{m=\infty } {\frac{a}{m\cdot \pi \cdot b}\cdot \left\{
{\left[ {2\cdot m\cdot \pi \cdot \frac{b}{a}\cdot sh\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right]\cdot \left[ {\left( {1-\nu +\left( {1+\nu }
\right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot \pi \cdot
\frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot \frac{b-z}{a}}
\right)-} \right.} \right.}
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b-z}{a}\cdot
sh\left( {m\cdot \pi \cdot \frac{b-z}{a}} \right)} \right]+\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)+\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {1-\nu +\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)} \right.-
\]
\[
\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot \frac{z}{a}\cdot
sh\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]+\left[
{sh^{2}\left( {m\cdot \pi \cdot \frac{b}{a}} \right)-\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)^{2}} \right]\cdot \left[ {\left( {3+\nu +\left(
{1+\nu } \right)\cdot m\cdot \pi \cdot \frac{b}{a}\cdot cth\left( {m\cdot
\pi \cdot \frac{b}{a}} \right)} \right)\cdot ch\left( {m\cdot \pi \cdot
\frac{z}{a}} \right)-} \right.
\]
\[
\left. {\left. {-\left( {1+\nu } \right)\cdot m\cdot \pi \cdot
\frac{z}{a}\cdot sh\left( {m\cdot \pi \cdot \frac{z}{a}} \right)} \right]}
\right\} \cdot \frac{\left[ {1+\left( {-1} \right)^{m+1}} \right]\cdot
sin\left( {m\cdot \pi \cdot \frac{x}{a}} \right)}{m\cdot \pi \cdot sh\left(
{m\cdot \pi \cdot \frac{b}{a}} \right)\cdot \left[ {sh^{2}\left( {m\cdot \pi
\cdot \frac{b}{a}} \right)-\left( {m\cdot \pi \cdot \frac{b}{a}}
\right)^{2}} \right]}.
\]
