Bending of a Symmetric Wedge by a Uniformly Distributed Load Applied to the Surface of One of the Faces of the Wedge (Levi Problem)
Objective: Determination of the stress state of a symmetric wedge of unit thickness in polar coordinates subjected to bending by a uniformly distributed load applied to the surface of one of the faces of the wedge.
Initial data file: 4_24.spr
Problem formulation: The uniformly distributed load q acting in the plane of the wedge along the Ox2 axis is applied to the surface of one of the faces of the wedge of unit thickness. Determine the stress tensor components in polar coordinates σrr, σθθ, σrθ at a radial distance r = 5.0 m from the vertex of the wedge.
References: S.P. Demidov, Theory of Elasticity. — Moscow: High school, 1979.
Initial data:
| E = 3.0·107 kPa | - elastic modulus; |
| μ = 0.2 | - Poisson’s ratio; |
| h = 1.0 m | - thickness of the wedge; |
| α = 30º | - apex angle of the wedge; |
| R = 15.0 m | - radius of the fixed end of the wedge; |
| q = 10.0 kN/m | - uniformly distributed load bending the wedge. |
Finite element model: Design model – general type system, wedge elements – 290 eight-node elements of type 50 and 10 six-node elements of type 45. The spacing of the finite element mesh in the radial direction is 0.5 m, and in the tangential direction is 3º. The direction of the output of internal forces is radial tangential. Since there are no forces distributed according to the law of the analytical solution at the fixed end of the wedge, in order to obtain an exact solution at the radial distance r = 5.0 m from the action of the uniformly distributed load q the radial distance to the fixed end is taken as R = 15.0 м. Number of nodes in the design model – 961.
Results in SCAD


Design model

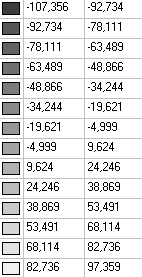
Values of stresses σrr (kN/m2) under the action of the uniformly distributed load q
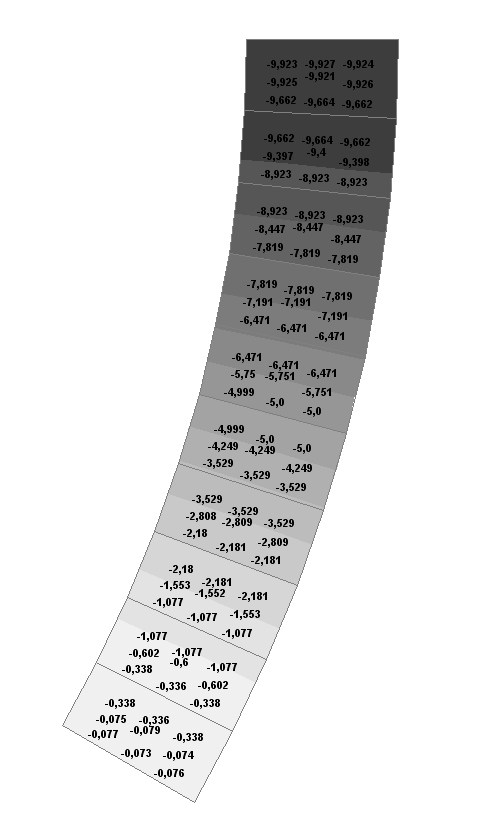
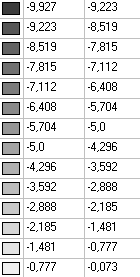
Values of stresses σθθ (kN/m2) under the action of the uniformly distributed load q

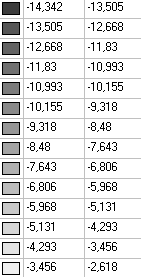
Values of stresses σrθ (kN/m2) under the action of the uniformly distributed load q
Comparison of solutions:
Stress tensor components at a radial distance r = 5.0 m from the vertex of the wedge under the uniformly distributed load q.
|
Angle θ |
Stresses σrr (kN/m2) |
Stresses σθθ (kN/m2) |
Stresses σrθ (kN/m2) |
|||
|---|---|---|---|---|---|---|
|
Theory |
SCAD |
Theory |
SCAD |
Theory |
SCAD |
|
|
0º |
97.4110 |
97.3548 |
-10.0000 |
-9.9243 |
0.0000 |
-2.7111 |
|
15º |
-5.0000 |
-5.0011 |
-5.0000 |
-5.0000 |
-14.3903 |
-14.2629 |
|
30º |
-107.4110 |
-107.3501 |
0.0000 |
-0.0757 |
0.0000 |
-2.7108 |
Notes: In the analytical solution the stresses σrr, σθθ, σrθ in the body of the wedge subjected to the uniformly distributed load q are determined according to the following formulas (S.P. Demidov, Theory of Elasticity. — Moscow: High school, 1979, p. 276):
\[ \sigma_{rr} =\frac{q}{2\cdot K}\cdot \left[ {2\cdot \alpha -2\cdot \theta -\left( {1-\cos \left( {2\cdot \theta } \right)} \right)\cdot tg\alpha -\sin \left( {2\cdot \theta } \right)} \right]; \] \[ \sigma_{\theta \theta } =\frac{q}{2\cdot K}\cdot \left[ {2\cdot \alpha -2\cdot \theta -\left( {1+\cos \left( {2\cdot \theta } \right)} \right)\cdot tg\alpha +\sin \left( {2\cdot \theta } \right)} \right] \] \[\sigma_{r\theta } =\frac{q}{2\cdot K}\cdot \left[ {1-tg\alpha \cdot \sin \left( {2\cdot \theta } \right)-\cos \left( {2\cdot \theta } \right)} \right], \quad where: \] \[ K=tg\alpha -\alpha . \]
