Stress-Strain State of a Simply Supported Annular Plate Subjected to a Uniformly Distributed Transverse Load
Objective: Determination of the stress-strain state of a simply supported annular plate of constant thickness subjected to a uniformly distributed transverse load.
Initial data file: 4_16.spr
Problem formulation: The simply supported annular plate of constant thickness is subjected to the uniformly distributed transverse load. Determine the deflection w, the radial Mr and tangential Mθ bending moments along the internal and external contour of the plate.
References: S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948.
Initial data:
| E = 2.0·108 kPa | - elastic modulus; |
| μ = 0.3 | - Poisson’s ratio; |
| R = 1.2 m | - outer radius of the plate; |
| r = 0.6 m | - inner radius of the plate; |
| h = 2.0·10-2 m | - thickness of the plate; |
| p = 10 kPa | - uniformly distributed transverse load. |
Finite element model: Design model – general type system, plate elements – 288 eight-node elements of type 50. The direction of the output of internal forces is radial tangential. Boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z along the external contour of the plate. Number of nodes in the design model – 960.
Results in SCAD
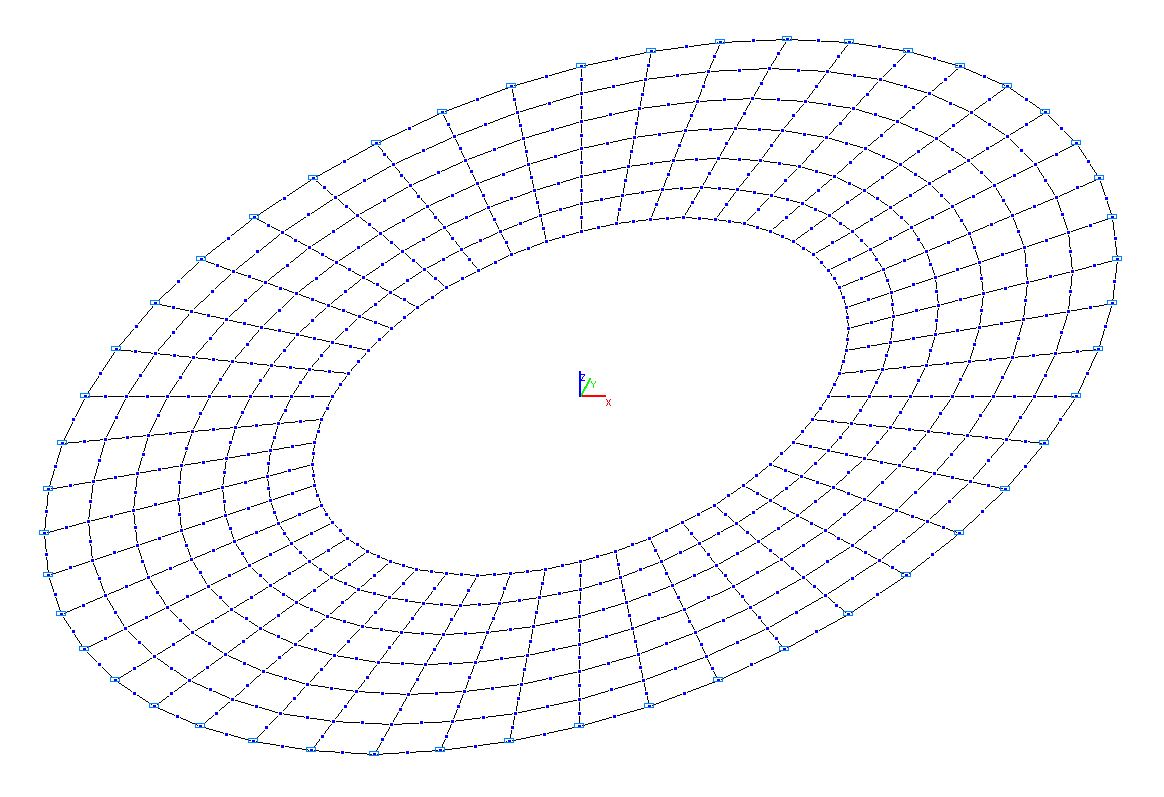
Design model
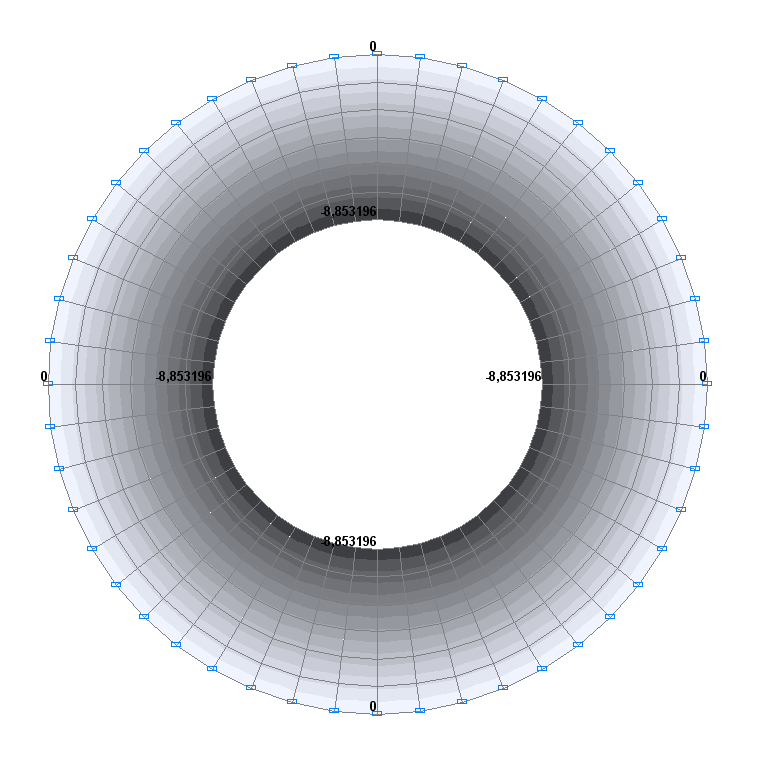

Values of deflections w (mm)


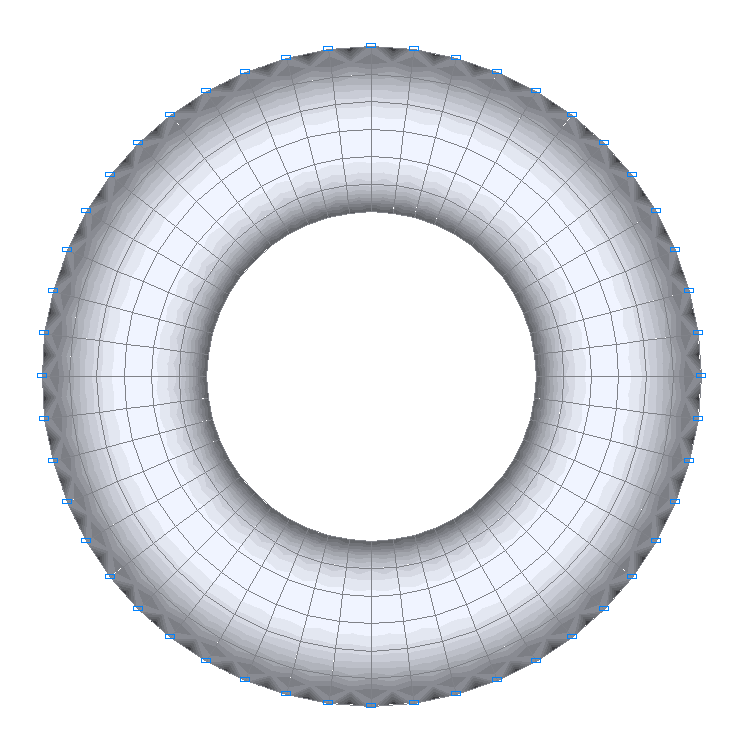

Values of radial bending moments Mr (kN·m/m)
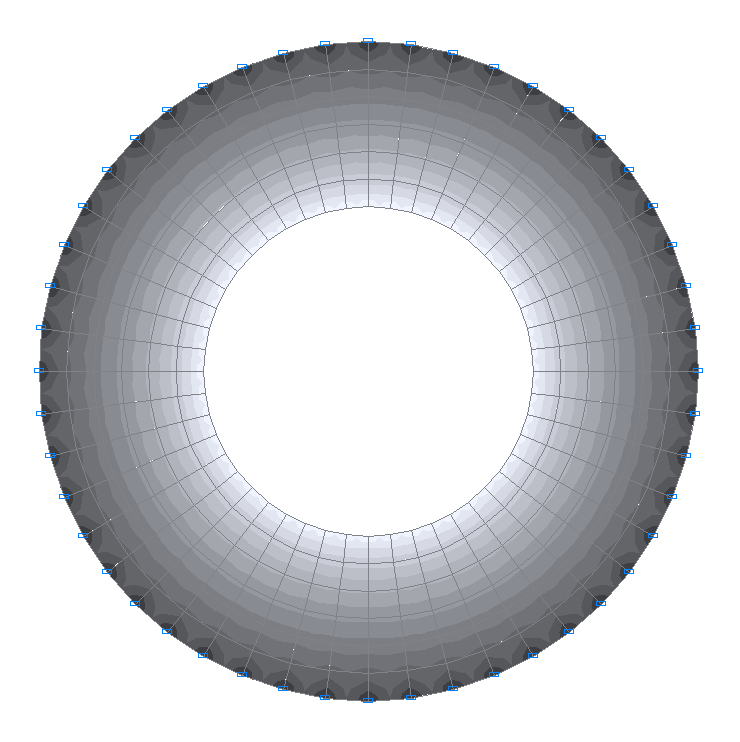
Values of tangential bending moments Mθ (kN·m/m)
Comparison of solutions:
|
Parameter |
Along the internal contour of the plate |
Along the external contour of the plate |
||||
|---|---|---|---|---|---|---|
|
Theory |
SCAD |
Deviations, % |
Theory |
SCAD |
Deviations, % |
|
|
w, mm |
-8.933 |
-8.863 |
0.78 |
0.000 |
0.000 |
─ |
|
Mr, kN·m/m |
0.000 |
0.001 |
─ |
0.000 |
0.052 |
─ |
|
Mθ, kN·m/m |
3.462 |
3.474 |
0.35 |
1.574 |
1.547 |
1.72 |
Notes: In the analytical solution the deflection w, the radial Mr and tangential Mθ bending moments along the internal contour of the plate can be determined according to the following formulas (S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948. p. 71):
\[w=-\frac{q}{64\cdot D}\cdot \left[ {\frac{R^{2}-r^{2}}{1+\mu }\cdot \left( {R^{2}\cdot \left( {5+\mu } \right)-r^{2}\cdot \left( {7+2\cdot \mu } \right)} \right)-\frac{4\cdot R^{2}\cdot r^{2}}{1-\mu }\cdot \ln \frac{r}{R}\cdot \left( {3+\mu +\frac{4\cdot r^{2}}{R^{2}-r^{2}}\cdot \left( {1+\mu } \right)\cdot \ln \frac{r}{R}} \right)} \right], where: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}; \] \[ M_{r} =0; \] \[ M_{\theta } =\frac{q}{8}\cdot \left[ {R^{2}\cdot \left( {3+\mu } \right)-r^{2}\cdot \left( {1-\mu } \right)+\frac{4\cdot R^{2}\cdot r^{2}}{R^{2}-r^{2}}\cdot \ln \frac{r}{R}\cdot \left( {1+\mu } \right)} \right]. \]
In the analytical solution the deflection w, the radial Mr and tangential Mθ bending moments along the external contour of the plate can be determined according to the following formulas (S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948. p. 71):
\[ w=0; \] \[ M_{r} =0; \] \[ M_{\theta } =\frac{q}{8}\cdot \left[ {R^{2}\cdot \left( {1-\mu } \right)+r^{2}\cdot \left( {1+3\cdot \mu } \right)+\frac{4\cdot R^{4}}{R^{2}-r^{2}}\cdot \ln \frac{r}{R}\cdot \left( {1+\mu } \right)} \right]. \]
