Square Plate Simply Supported along the Perimeter Subjected to a Uniformly Distributed Load

Objective: Determination of maximum displacements and bending moments in a square plate simply supported along the perimeter and subjected to a uniformly distributed load p.

Initial data file: 4_17.spr

Problem formulation: The square isotropic plate of constant thickness is simply supported along the perimeter and subjected to the uniformly distributed load p. Determine: maximum displacements and bending moments.

References: Strength, Stability, Vibrations. Handbook in three volumes. Volume 1. Ed. I.A. Birger and Ya.G. Panovko. — M.: Mechanical engineering, 1968, p. 532-535

Initial data:

E = 2.0·108 kPa	- elastic modulus,
μ = 0.3	- Poisson’s ratio,
a = 1.5 м	- size of the plate sides,
h = 0.01 м	- thickness of the plate,
р = 10 kPa	- normal pressure,

Constraints: hinge restraint of nodes along the contour out of the XOY plane (displacement  w = 0)

Finite element model: Design model – grade beam, plate. Plate elements – 144 eight-node elements of type 20. Number of nodes in the design model – 481.

Results in SCAD

Design model

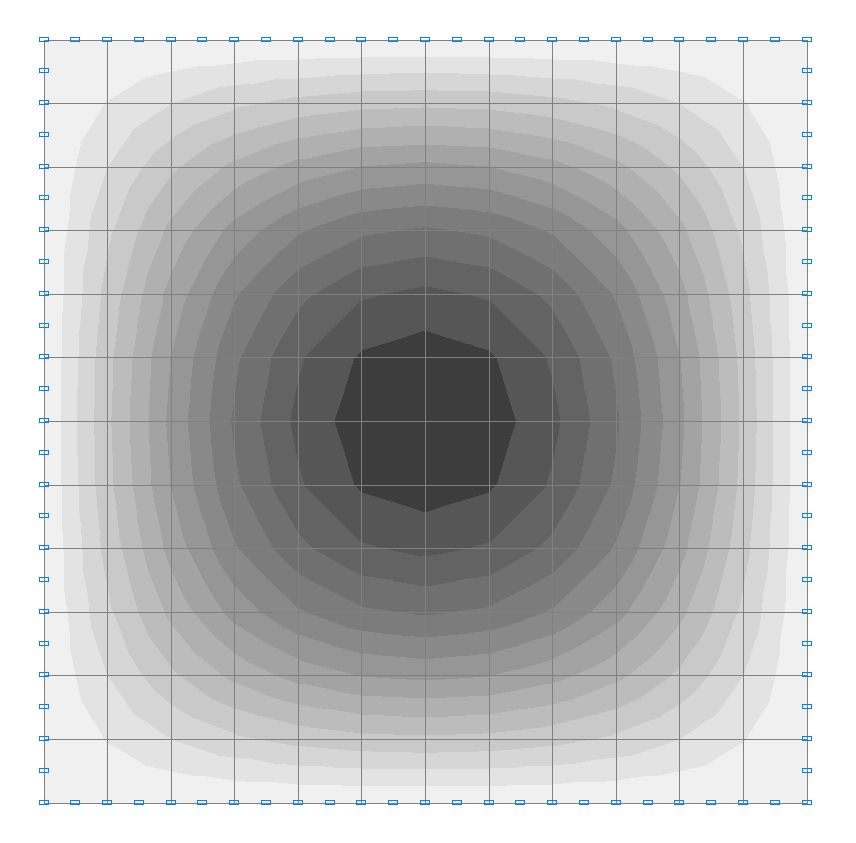
Values of displacements w (mm)

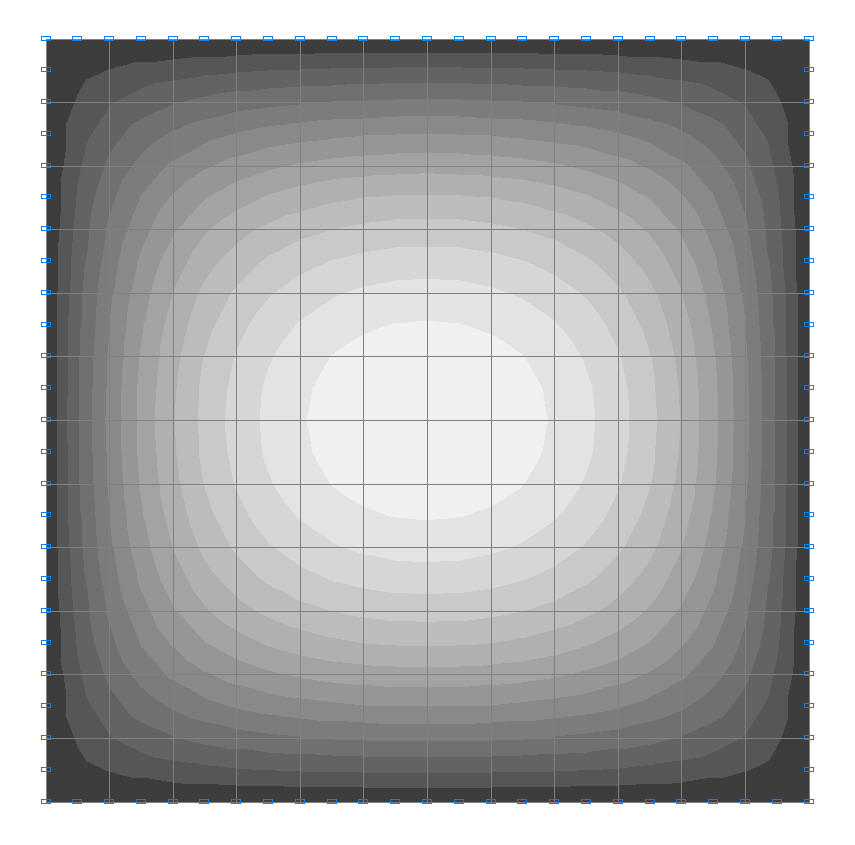
Values of bending moments M_x (kN·m/m)

Values of bending moments M_y (kN·m/m)

 

Comparison of solutions:

Parameter	Theory	SCAD	Deviations, %
Displacement in the center of the plate w, mm	11.22	11.23	0.09
Bending moment Мх, kN∙m /m	1.078	1.077	0.09
Bending moment Му, kN∙m /m	1.078	1.077	0.09

Notes: In the analytical solution the displacement w and the bending moments M_x and M_y in the center of the plate subjected to the uniformly distributed load are determined according to the following formulas (Handbook in three volumes. Volume 1. Ed. I.A. Birger and Ya.G. Panovko. — M.: Mechanical engineering, 1968, p. 532-535):

\[w=0.00406\cdot \frac{p\cdot a^{4}}{D}, where: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}; \] \[ M_{x} =M_{y} =0.0479\cdot p\cdot a^{2}. \]