Rectangular Plate Simply Supported at Three Vertices Subjected to a Concentrated Force and Concentrated Moments out of Its Plane
Objective: Determination of the strain state of a rectangular plate simply supported at three vertices and subjected to a concentrated force and concentrated moments out of its plane.
Initial data file: SSLS26_v11.3.spr
Problem formulation: The rectangular plate simply supported at three vertices (points A, B, D) is subjected to a concentrated force Fz out of its plane applied to the free vertex (point C), and concentrated moments Mx and My, applied in pairs to all four vertices (points A, B, C, D) with unilateral bending in planes parallel to the adjacent sides. Determine the displacement Z of the free vertex (point C) out of the plane of the plate.
References: J.L. Batoz, An explicit formulation for an efficient triangular plate-bending element, International Journal for Numerical Methods in Engineering, vol.18, John Wiley and Sons, 1982.
Initial data:
| E = 1.0·103 Pa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| h = 1.0 m | - thickness of the plate; |
| a = 40.0 m | - long side of the plate (along the X axis of the global coordinate system); |
| b = 20.0 m | - short side of the plate (along the Y axis of the global coordinate system); |
| Fz = 2.0 N | - value of the transverse concentrated force; |
| Mx = 20.0 N∙m | - value of the concentrated moments bending the plate along the short side (with respect to the X axis of the global coordinate system); |
| My = 10.0 N∙m | - value of the concentrated moments bending the plate along the long side (with respect to the Y axis of the global coordinate system). |
Finite element model: Design model – grade beam / plate, shell elements – 100 plate elements of type 20. Boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z in the vertices of the plate on the X and Y axes of the global coordinate system (points A, B, C). Number of nodes in the design model – 121.
Results in SCAD
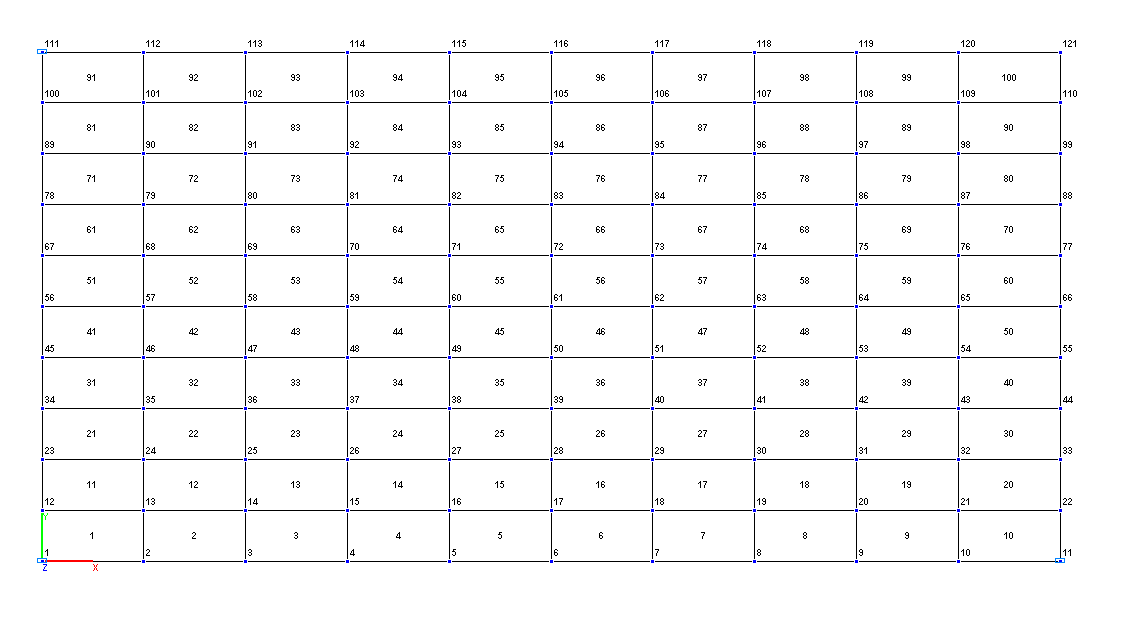
Design model
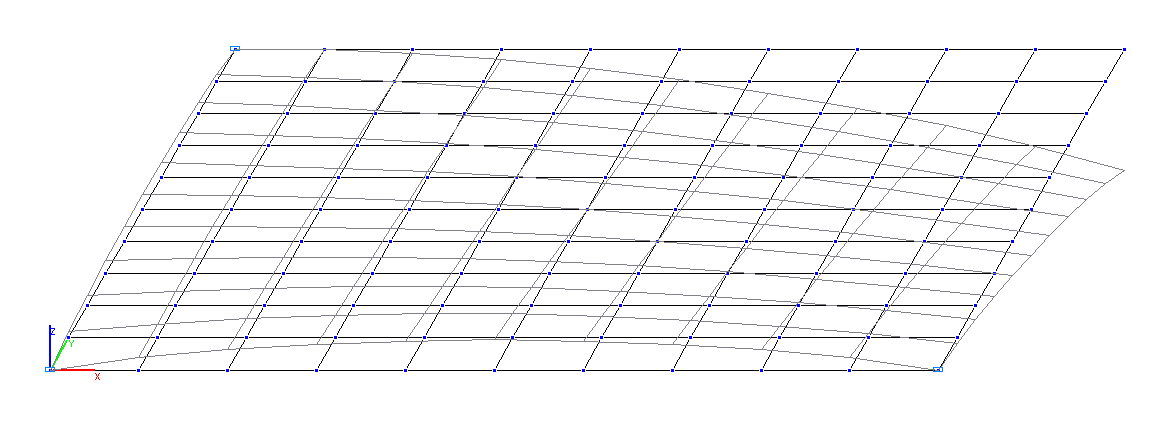
Deformed model
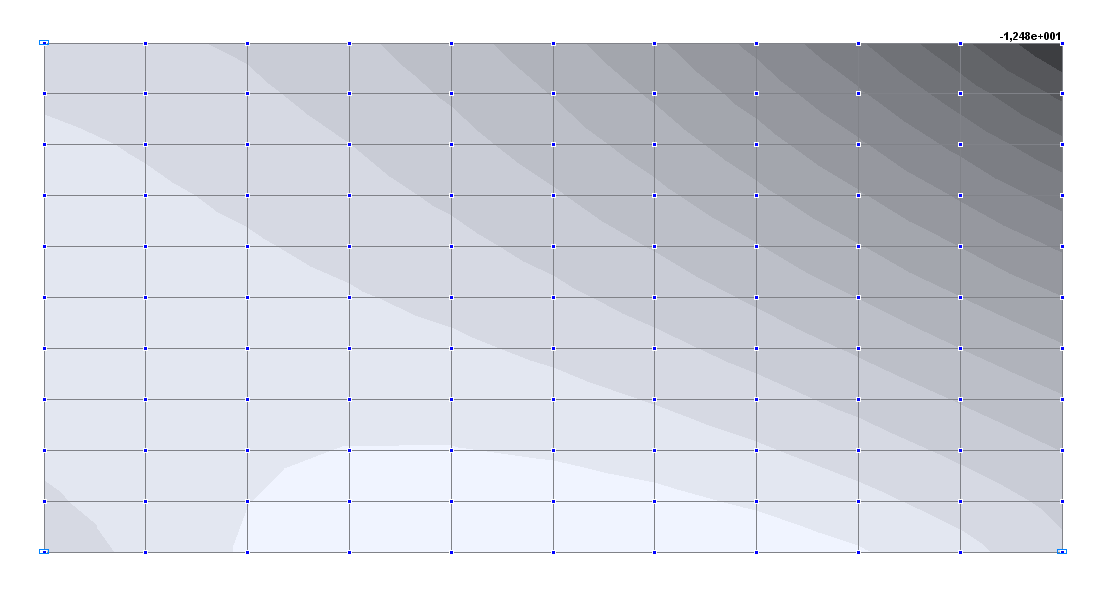
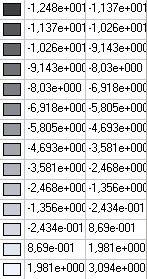
Values of transverse displacements Z (m)
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviation, % |
|---|---|---|---|
|
Displacement Z of the free vertex (point C), m |
-1.248∙101 |
-1.248∙101 |
0.00 |
