Stress-Strain State of a Clamped Hexagonal Plate Subjected to a Uniformly Distributed Load
Objective: Determination of displacements and bending moments in the center of a hexagonal plate clamped on all sides and subjected to a uniformly distributed load q.
Initial data file: 4_19.spr
Problem formulation: The regular hexagonal plate of constant thickness clamped on all sides is subjected to normal pressure q. Determine: the axial displacement w and bending moments Mx, My in the center of the plate.
References: Vainberg D. V., Handbook on Strength, Stability and Oscillations of Plates. Kiev: Budivelnik, 1973.
Initial data:
| E = 2.0·108 kPa | - elastic modulus, |
| μ = 0.3 | - Poisson’s ratio, |
| a = 0.134 m | - side of the hexagonal plate, |
| h = 0.003 m | - thickness of the plate, |
| q = 1000 kPa | - normal pressure, |
Constraints: rigid restraint of nodes along the contour (displacement w = 0)
Finite element model: Design model – general type system. Plate elements – 389 four-node elements of type 44 and 73 three-node elements of type 42. Number of nodes in the design model – 451.
Results in SCAD

Design model
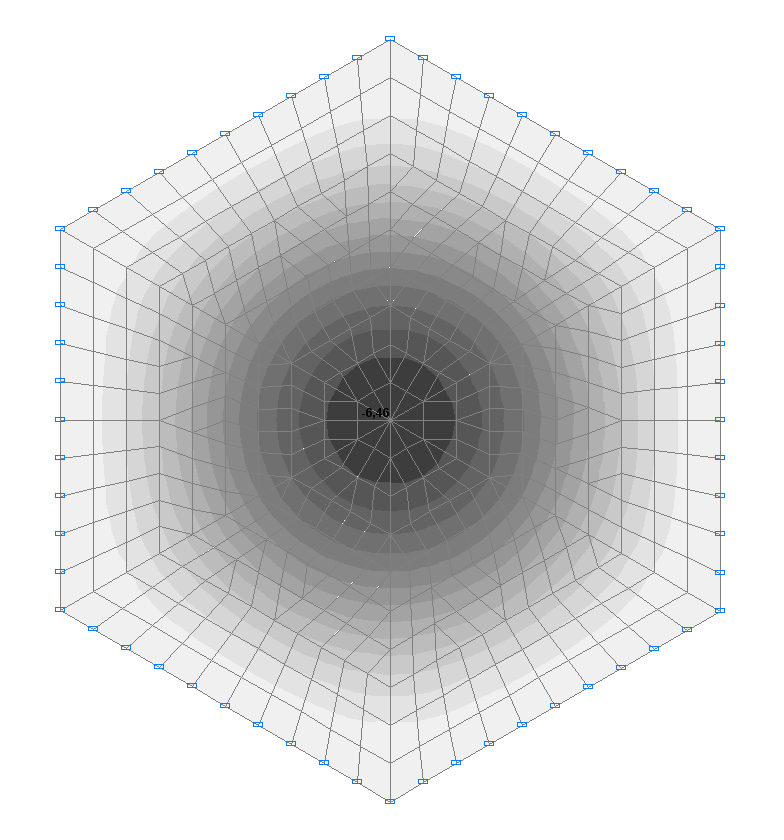

Values of displacements w (mm)


Values of bending moments Mx (kN·m/m)


Values of bending moments My (kN·m/m)
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
Displacement in the center of the plate w, mm |
6.51 |
6.46 |
0.77 |
|
Bending moment Мх, kN∙m /m |
1.163 |
1.171 |
0.69 |
|
Bending moment Му, kN∙m /m |
1.163 |
1.171 |
0.69 |
Notes: In the analytical solution the displacement w and bending moments Mx and My in the center of the plate can be determined according to the following formulas (Vainberg D. V., Handbook on Strength, Stability and Oscillations of Plates. Kiev: Budivelnik, 1973):
\[w=0.009979\cdot \frac{q\cdot a^{4}}{D}, where: \]\[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu^{2}} \right)}; \] \[ M_{x} =M_{y} =0.049835\cdot \left( {1+\mu } \right)\cdot q\cdot a^{2}. \]
