Cylindrical Shell with Simply Supported Edges Subjected to Uniform Internal Pressure
Objective: Determination of the stress-strain state of a cylindrical shell with simply supported edges subjected to the internal pressure.
Initial data file: 4_31.spr
Problem formulation: The cylindrical thin-walled shell simply supported along the edges is subjected to uniform internal pressure p. Determine the bending moments and longitudinal forces acting on the midsurface of the shell in the meridian Mx, Nx and circumferential Mφ, Nφ directions, as well as the radial displacements w for the cross-section in the middle of the span.
References: S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948.
Initial data:
| E = 2.1·108 kPa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| h = 0.02 m | - thickness of the shell; |
| a = 10.0 m | - radius of the midsurface of the shell; |
| l = 2.0 m | - length of the shell; |
| p = 10.0 kPa | - internal pressure. |
Finite element model: Design model – general type system, shell elements – 9216 four-node elements of type 44. The spacing of the finite element mesh in the meridian direction is 0.0625 m and in the circumferential direction is 1.25º. The boundary conditions at the simply supported edges are provided by imposing constraints in the directions of the angular and linear displacements in their plane. Number of nodes in the design model – 9504.
Results in SCAD


Design and deformed models
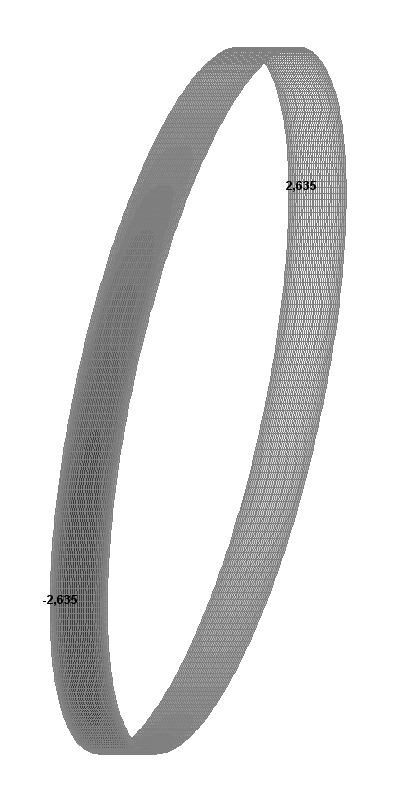



Values of radial displacements w (mm)
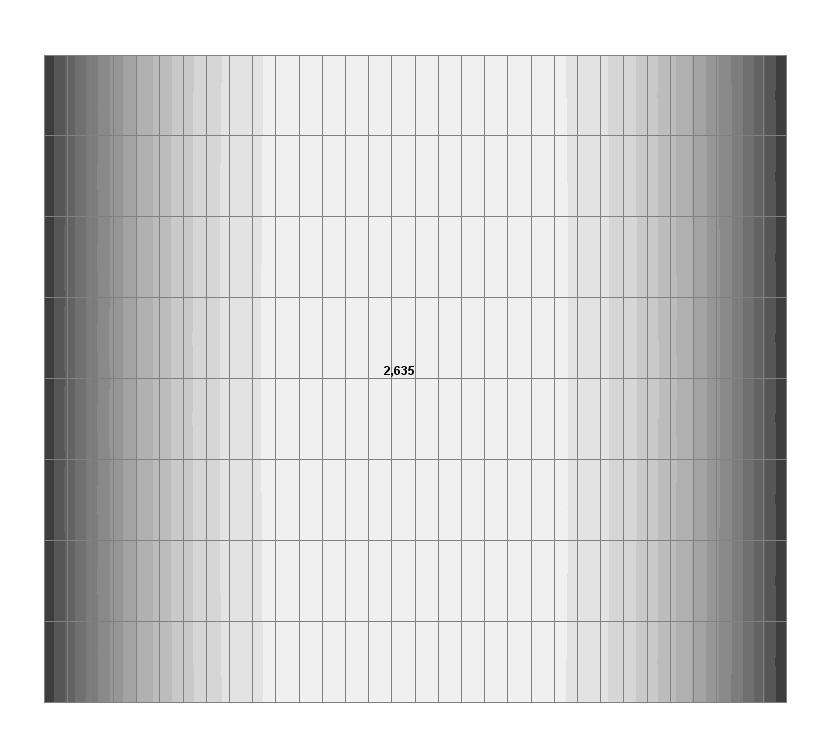
Values of radial displacements w (mm) for the fragment of the model from the section in the area of the horizontal diameter with the central angle of 5.00º

Values of bending moments acting on the midsurface of the shell in the meridian direction Mx (kN∙m/m)

Values of bending moments acting on the midsurface of the shell in the meridian direction Mx (kN∙m/m) for the fragment of the model from the section in the area of the horizontal diameter with the central angle of 5.00º

Values of bending moments acting on the midsurface of the shell in the circumferential direction Mφ (kN∙m/m)


Values of bending moments acting on the midsurface of the shell in the circumferential direction Mφ (kN∙m/m) for the fragment of the model from the section in the area of the horizontal diameter with the central angle of 5.00º

Values of longitudinal forces acting on the midsurface of the shell in the meridian direction Nx (kN/m2)

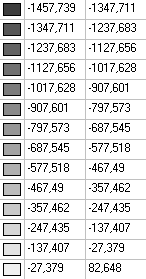
Values of longitudinal forces acting on the midsurface of the shell in the meridian direction Nx (kN/m2) for the fragment of the model from the section in the area of the horizontal diameter with the central angle of 5.00º

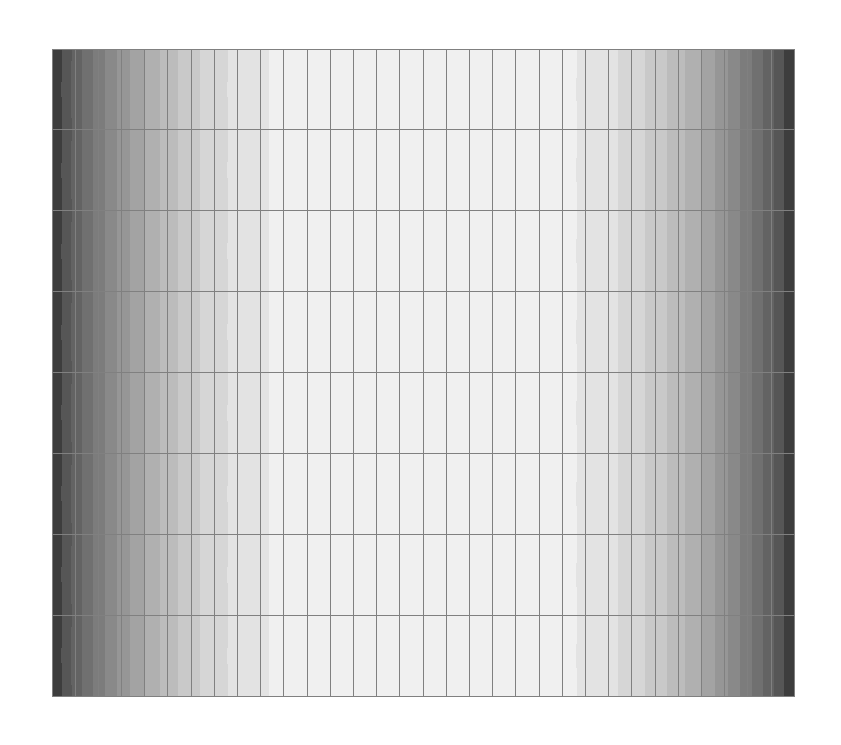
Values of longitudinal forces acting on the midsurface of the shell in the circumferential direction Nφ (kN/m2) 


Values of longitudinal forces acting on the midsurface of the shell in the circumferential direction Nφ (kN/m2) for the fragment of the model from the section in the area of the horizontal diameter with the central angle of 5.00º
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
w(l/2), mm |
2.640 |
2.635 |
0.19 |
|
Mx(l/2), kN∙m/m |
0.178969 |
0.180453 |
0.83 |
|
Mφ(l/2), kN∙m/m |
0.053691 |
0.054136 |
0.83 |
|
Nx(l/2), kN/m |
0.000 |
8.238∙0.02 = 0.165 |
─ |
|
Nφ(l/2), kN/m |
1108.655 |
55346.398∙0.02 = 1106.928 |
0.16 |
Notes: In the analytical solution the bending moments and longitudinal forces acting on the midsurface of the shell in the meridian Mx, Nx and circumferential Mφ, Nφ directions, as well as the radial displacements w for the cross-section in the middle of the span can be determined according to the following formulas (S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948, p. 377):
\[ w=\frac{p\cdot l^{4}}{64\cdot D\cdot \alpha^{4}}\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right)=\frac{p\cdot a^{2}}{E\cdot h}\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right); \] \[ M_{x} =\frac{p\cdot l^{2}}{4\cdot \alpha^{2}}\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}=\frac{p\cdot a\cdot h}{\sqrt {3\cdot \left( {1-\nu^{2}} \right)} }\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}; \] \[ M_{\phi } =\nu \cdot M_{x} =\frac{p\cdot a\cdot h\cdot \nu }{\sqrt {3\cdot \left( {1-\nu^{2}} \right)} }\cdot \frac{\sin \left( \alpha \right)\cdot sh\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}; \] \[ \quad N_{x} =0; \quad N_{\phi } =-\frac{E\cdot h}{a}\cdot w=-p\cdot a\cdot \left( {1-\frac{2\cdot \cos \left( \alpha \right)\cdot ch\left( \alpha \right)}{\cos \left( {2\cdot \alpha } \right)+ch\left( {2\cdot \alpha } \right)}} \right), \quad where: \]\[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad \beta =\sqrt[4]{\frac{3\cdot \left( {1-\nu^{2}} \right)}{a^{2}\cdot h^{2}}}, \quad \alpha =\frac{\beta \cdot l}{2}. \]
