Cylindrical Shell with Free Edges at a Temperature Gradient across the Thickness (in the Radial Direction)
Objective: Determination of the stress-strain state of a cylindrical shell with free edges subjected to a temperature gradient across the thickness.
Initial data file: 4_33.spr
Problem formulation: The cylindrical thin-walled shell free from constraints is subjected to a temperature gradient across the thickness. The temperatures of the cylinder wall on its internal t1 and external surfaces t2 are constant. The temperature varies linearly across the thickness of the wall. Determine the stress tensor components on the internal and external surfaces of the shell in the meridian σxext (σxint) and circumferential σφext (σφint) directions, as well as the radial displacements w.
References: S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948.
Initial data:
| E = 2.1·108 kPa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| h = 0.02 m | - thickness of the shell wall; |
| a = 1.0 m | - radius of the midsurface of the shell wall; |
| l = 4.0 m | - length of the shell; |
| α = 0.12·10-4 1/ºC | - linear expansion coefficient; |
| t1 = 20 ºC | - temperature on the internal surface of the cylinder wall; |
| t2 = 0 ºC | - temperature on the external surface of the cylinder wall; |
Finite element model: Design model – general type system, shell elements – 12800 four-node elements of type 44. The spacing of the finite element mesh in the meridian direction is 0.025 m and in the circumferential direction is 4.5º. The dimensional stability of the design model is provided by imposing constraints according to its symmetry conditions. Number of nodes in the design model – 12880.
Results in SCAD
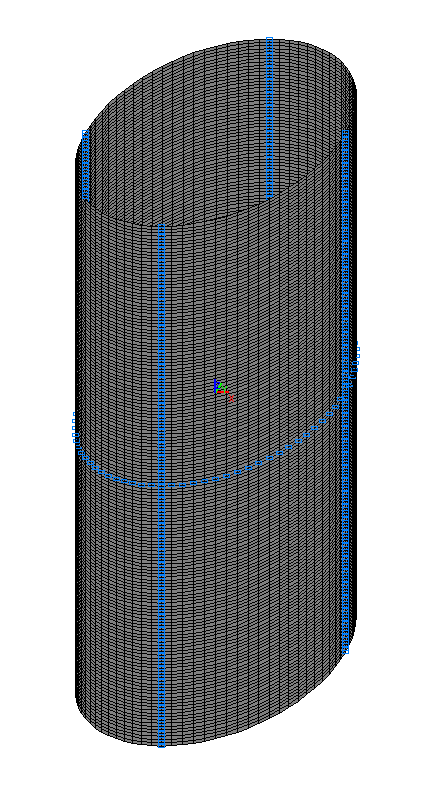
Design model
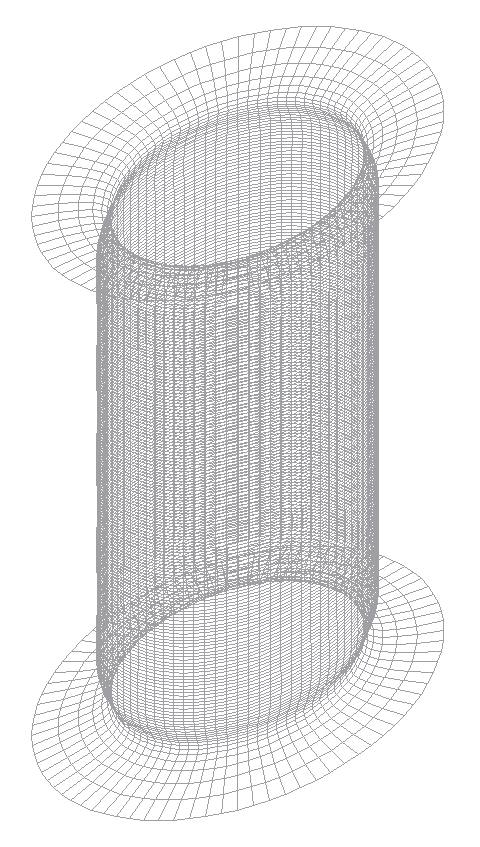
Deformed model


Values of radial displacements w (mm)


Values of radial displacements w (mm) for the fragment of the model from the section with the central angle of 18.0º
Values of stresses on the external surface of the shell in the meridian direction σxext (kN/m2)

Values of stresses on the internal surface of the shell in the meridian direction σxint (kN/m2)

Values of stresses on the external surface of the shell in the circumferential direction σφext (kN/m2)


Values of stresses on the internal surface of the shell in the circumferential direction σφint (kN/m2)
Comparison of solutions:
|
x, m |
w, mm |
||
|---|---|---|---|
|
Theory |
SCAD |
Deviations, % |
|
|
0.200 |
-18.61∙10-3 |
-18.01∙10-3 |
3.22 |
|
0.250 |
-13.71∙10-3 |
-13.20∙10-3 |
3.72 |
|
0.300 |
-8.14∙10-3 |
-7.81∙10-3 |
4.05 |
|
0.350 |
-3.76∙10-3 |
-3.60∙10-3 |
4.26 |
|
0.400 |
-1.01∙10-3 |
-0.97∙10-3 |
3.96 |
|
0.450 |
0.36∙10-3 |
0.34∙10-3 |
5.56 |
|
0.500 |
0.82∙10-3 |
0.78∙10-3 |
4.88 |
|
0.550 |
0.79∙10-3 |
0.75∙10-3 |
5.06 |
|
0.600 |
0.57∙10-3 |
0.54∙10-3 |
5.26 |
|
0.650 |
0.33∙10-3 |
0.32∙10-3 |
3.03 |
|
0.700 |
0.15∙10-3 |
0.14∙10-3 |
6.67 |
|
0.750 |
0.04∙10-3 |
0.04∙10-3 |
0.00 |
|
0.800 |
-0.02∙10-3 |
-0.02∙10-3 |
─ |
|
0.850 |
-0.04∙10-3 |
-0.03∙10-3 |
─ |
|
0.900 |
-0.03∙10-3 |
-0.03∙10-3 |
─ |
|
0.950 |
-0.02∙10-3 |
-0.02∙10-3 |
─ |
|
1.000 |
-0.01∙10-3 |
-0.01∙10-3 |
─ |
|
1.100 |
0 |
0 |
─ |
|
1.200 |
0 |
0 |
─ |
|
1.300 |
0 |
0 |
─ |
|
1.400 |
0 |
0 |
─ |
|
1.500 |
0 |
0 |
─ |
|
1.600 |
0 |
0 |
─ |
|
1.700 |
0 |
0 |
─ |
|
1.800 |
0 |
0 |
─ |
|
1.900 |
0 |
0 |
─ |
|
2.000 |
0 |
0 |
─ |
|
x, m |
σxext (kN/m2) |
σxint (kN/m2) |
||||
|---|---|---|---|---|---|---|
|
Theory |
SCAD |
Deviations, % |
Theory |
SCAD |
Deviations, % |
|
|
0.200 |
31761 |
32052 |
0.92 |
-31761 |
-32090 |
1.04 |
|
0.250 |
35560 |
35681 |
0.34 |
-35560 |
-35685 |
0.35 |
|
0.300 |
37206 |
37221 |
0.04 |
-37206 |
-37210 |
0.01 |
|
0.350 |
37553 |
37519 |
0.09 |
-37553 |
-37505 |
0.13 |
|
0.400 |
37286 |
37241 |
0.12 |
-37286 |
-37229 |
0.15 |
|
0.450 |
36841 |
36804 |
0.10 |
-36841 |
-36796 |
0.12 |
|
0.500 |
36441 |
36418 |
0.06 |
-36441 |
-36414 |
0.07 |
|
0.550 |
36164 |
36154 |
0.03 |
-36164 |
-36152 |
0.03 |
|
0.600 |
36010 |
36007 |
0.01 |
-36010 |
-36007 |
0.01 |
|
0.650 |
35945 |
35947 |
0.01 |
-35945 |
-35947 |
0.01 |
|
0.700 |
35933 |
35936 |
0.01 |
-35933 |
-35937 |
0.01 |
|
0.750 |
35946 |
35949 |
0.01 |
-35946 |
-35949 |
0.01 |
|
0.800 |
35965 |
35967 |
0.01 |
-35965 |
-35968 |
0.01 |
|
0.850 |
35982 |
35983 |
0.00 |
-35982 |
-35983 |
0.00 |
|
0.900 |
35994 |
35994 |
0.00 |
-35994 |
-35994 |
0.00 |
|
0.950 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.000 |
36002 |
36002 |
0.00 |
-36002 |
-36002 |
0.00 |
|
1.100 |
36002 |
36002 |
0.00 |
-36002 |
-36002 |
0.00 |
|
1.200 |
36001 |
36001 |
0.00 |
-36001 |
-36001 |
0.00 |
|
1.300 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.400 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.500 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.600 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.700 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.800 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.900 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
2.000 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
0.000 |
45027 |
44606 |
0.93 |
-5373 |
-5794 |
7.84 |
|
0.025 |
37510 |
37025 |
1.29 |
-13846 |
-14584 |
5.33 |
|
0.050 |
32614 |
32413 |
0.62 |
-21047 |
-21639 |
2.81 |
|
0.075 |
29785 |
29786 |
0.00 |
-26849 |
-27290 |
1.64 |
|
0.100 |
28500 |
28633 |
0.47 |
-31284 |
-31586 |
0.97 |
|
0.150 |
28809 |
29047 |
0.83 |
-36646 |
-36735 |
0.24 |
|
0.200 |
30819 |
31034 |
0.70 |
-38637 |
-38608 |
0.08 |
|
0.250 |
32988 |
33133 |
0.44 |
-38748 |
-38677 |
0.18 |
|
0.300 |
34652 |
34726 |
0.21 |
-38072 |
-38003 |
0.18 |
|
0.350 |
35676 |
35700 |
0.07 |
-37256 |
-37208 |
0.13 |
|
0.400 |
36173 |
36169 |
0.01 |
-36598 |
-36572 |
0.07 |
|
0.450 |
36328 |
36313 |
0.04 |
-36176 |
-36167 |
0.02 |
|
0.500 |
36305 |
36289 |
0.04 |
-35960 |
-35961 |
0.00 |
|
0.550 |
36215 |
36203 |
0.03 |
-35883 |
-35888 |
0.01 |
|
0.600 |
36123 |
36116 |
0.02 |
-35883 |
-35888 |
0.01 |
|
0.650 |
36053 |
36050 |
0.01 |
-35914 |
-35918 |
0.01 |
|
0.700 |
36011 |
36011 |
0.00 |
-35949 |
-35951 |
0.01 |
|
0.750 |
35991 |
35992 |
0.00 |
-35976 |
-35977 |
0.00 |
|
0.800 |
35986 |
35987 |
0.00 |
-35993 |
-35994 |
0.00 |
|
0.850 |
35987 |
35988 |
0.00 |
-36002 |
-36002 |
0.00 |
|
0.900 |
35991 |
35992 |
0.00 |
-36005 |
-36005 |
0.00 |
|
0.950 |
35995 |
35995 |
0.00 |
-36005 |
-36005 |
0.00 |
|
1.000 |
35998 |
35998 |
0.00 |
-36004 |
-36003 |
0.00 |
|
1.100 |
36000 |
36000 |
0.00 |
-36001 |
-36001 |
0.00 |
|
1.200 |
36001 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.300 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.400 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.500 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.600 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.700 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.800 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
1.900 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
|
2.000 |
36000 |
36000 |
0.00 |
-36000 |
-36000 |
0.00 |
Notes: In the analytical solution the stresses on the internal and external surfaces of the shell in the meridian σxext (σxint) and circumferential σφext (σφint) directions, as well as the radial displacements w can be determined according to the following formulas (S.P. Timoshenko, Theory of Plates and Shells. — Moscow: OGIZ. Gostekhizdat, 1948, p. 399), which give a good approximation “at points at a considerable distance from the edges of the shell”:
\[ w=0.5\cdot \alpha \cdot \left( {t_{1} -t_{2} } \right)\cdot a\cdot \sqrt {\frac{1+\nu }{3\cdot \left( {1-\nu } \right)}} \cdot e^{-\beta \cdot x}\cdot \left( {\sin \left( {\beta \cdot x} \right)-\cos \left( {\beta \cdot x} \right)} \right); \] \[ \sigma_{x}^{ext} =\frac{E\cdot \alpha \cdot \left( {t_{1} -t_{2} } \right)}{2\cdot \left( {1-\nu } \right)}\cdot \left[ {-1+e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\sin \left( {\beta \cdot x} \right)} \right)} \right]; \] \[ \sigma_{x}^{int} =\frac{E\cdot \alpha \cdot \left( {t_{1} -t_{2} } \right)}{2\cdot \left( {1-\nu } \right)}\cdot \left[ {1-e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\sin \left( {\beta \cdot x} \right)} \right)} \right]; \] \[ \sigma_{\phi }^{ext} =\frac{E\cdot \alpha \cdot \left( {t_{1} -t_{2} } \right)}{2\cdot \left( {1-\nu } \right)}\cdot \left[ {-1+\nu \cdot e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\sin \left( {\beta \cdot x} \right)} \right)-\sqrt {\frac{1-\nu^{2}}{3}} \cdot e^{-\beta \cdot x}\cdot \left( {\sin \left( {\beta \cdot x} \right)-\cos \left( {\beta \cdot x} \right)} \right)} \right]; \] \[\sigma_{\phi }^{int} =\frac{E\cdot \alpha \cdot \left( {t_{1} -t_{2} } \right)}{2\cdot \left( {1-\nu } \right)}\cdot \left[ {1-\nu \cdot e^{-\beta \cdot x}\cdot \left( {\cos \left( {\beta \cdot x} \right)+\sin \left( {\beta \cdot x} \right)} \right)-\sqrt {\frac{1-\nu^{2}}{3}} \cdot e^{-\beta \cdot x}\cdot \left( {\sin \left( {\beta \cdot x} \right)-\cos \left( {\beta \cdot x} \right)} \right)} \right], where: \]\[ \beta =\sqrt[4]{\frac{3\cdot \left( {1-\nu^{2}} \right)}{a^{2}\cdot h^{2}}}. \]