Thick Circular Slab Clamped along the Side Surface Subjected to a Load Uniformly Distributed over the Upper Face
Objective: Determination of the stress-strain state of a thick circular slab clamped along the side surface subjected to a load uniformly distributed over the upper face in accordance with the spatial problem of the theory of elasticity.
SCAD version used: 21.1
Initial data files:
|
File name |
Description |
|---|---|
|
Design model for the slab thickness of 4 m |
|
|
Design model for the slab thickness of 6 m |
Problem formulation: The thick circular slab is clamped along the side surface and subjected to a load q uniformly distributed over the upper face. Determine:
- distribution of the radial σr and vertical σz normal stresses across the slab thickness in its center (r = 0);
- distribution of the vertical displacements w across the slab thickness in its center (r = 0).
References: Solyanik-Krassa K.V. Axisymmetric Problem of the Theory of Elasticity. – M.: Stroyizdat. 1987.
p. 336.
Initial data:
| E = 1.0·107 kPa | - elastic modulus; |
| μ = 0.25 | - Poisson’s ratio; |
| 2∙a = 20.0 m | - diameter of the slab; |
| 2∙h = 4.0 m; 6.0 m | - thickness of the slab; |
| q = 10 kPa | - load uniformly distributed over the upper face. |
Finite element model
The spacing of the finite element mesh of the slab in plan in the radial direction is 0.5 m and there are 16 layers of finite elements along the thickness (models 1х1).
Elements of the design model:
- 4384 solid twenty-node isoparametric elements of type 37 (parallelepiped);
- 400 solid fifteen-node isoparametric elements of type 35 (triangular prism).
Number of nodes in the design model – 20866.
The calculation was performed taking into account the symmetry planes. The constraints were imposed:
- on the side surface in the directions of all the linear degrees of freedom;
- on the YOZ plane – along the x axis;
- on the XOZ plane – along the y axis.
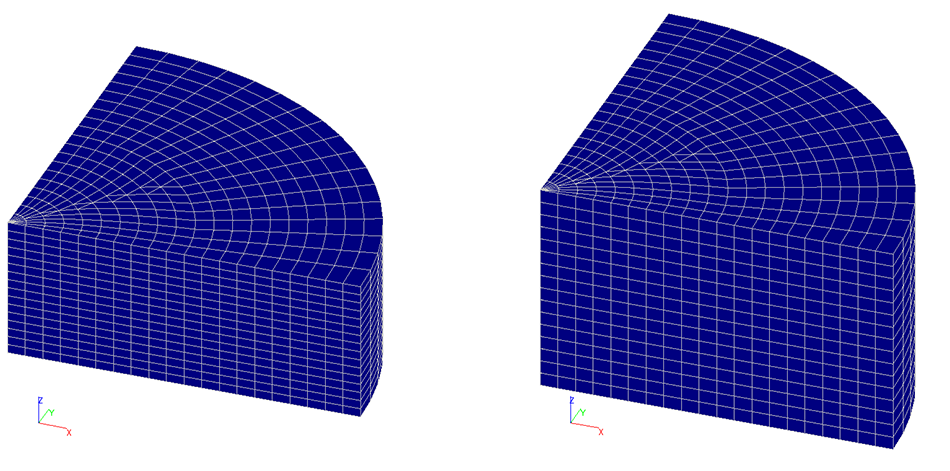
Design models of 4.0 m and 6.0 m thick slabs
Results in SCAD
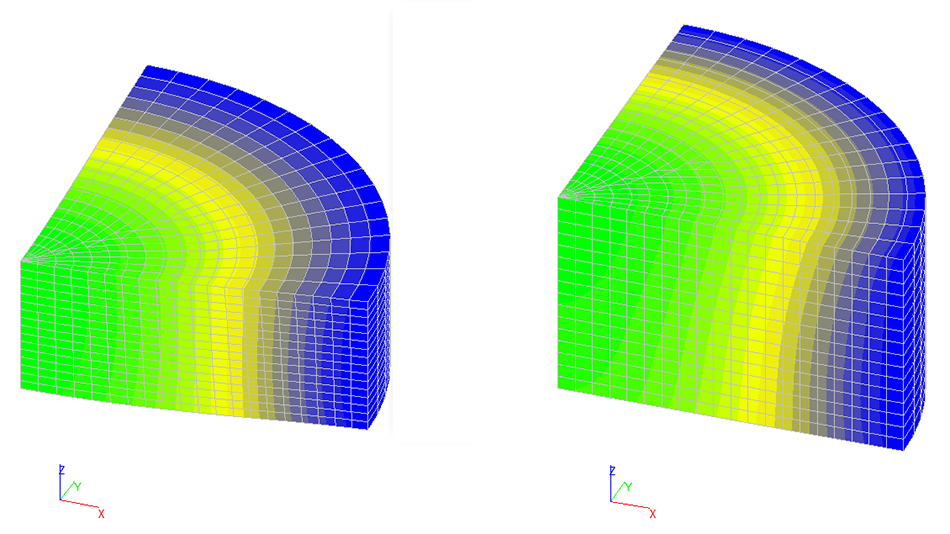
Values of vertical displacements w (mm) in 4.0 m and 6.0 m thick slabs
Comparison of solutions:
|
Thickness |
Value |
Point |
Approximate theory |
SCAD |
Deviation (%) |
|---|---|---|---|---|---|
|
4m |
w(mm) |
(0,0,2) |
-0.0436 |
-0.04538 |
4.08 |
|
(0,0,0) |
-0.0424 |
-0.0454 |
7.08 |
||
|
(0,0,-2) |
-0.0411 |
-0.04364 |
6.18 |
||
|
σr=σθ (kPa) |
(0,0,2) |
-34.51 |
-33.78 |
2.12 |
|
|
(0,0,0) |
-1.6667 |
-1.5547 |
6.72 |
||
|
(0,0,-2) |
31.1719 |
30.62 |
1.76 |
||
|
σz (kPa) |
(0,0,2) |
-10 |
-10.16 |
0.16 |
|
|
(0,0,0) |
-5 |
-5.07 |
0.14 |
||
|
(0,0,-2) |
0 |
-0.05 |
– |
||
|
6m |
w |
(0,0,3) |
-0.02097 |
-0.02112 |
0.72 |
|
(0,0,0) |
-0.01916 |
-0.01994 |
4.07 |
||
|
(0,0,-3) |
-0.01722 |
-0.01851 |
7.49 |
||
|
σr=σθ (kPa) |
(0,0,3) |
-18.2292 |
-18.51 |
1.54 |
|
|
(0,0,0) |
-1.6667 |
-1.5149 |
9.12 |
||
|
(0,0,-3) |
14.896 |
14.4884 |
2.74 |
||
|
σz (kPa) |
(0,0,3) |
-10 |
-9.797 |
2.03 |
|
|
(0,0,0) |
-5 |
-5.0569 |
1.14 |
||
|
(0,0,-3) |
0 |
0.043 |
– |
Note 1: The approximate analytical values were calculated according to the formulas given on pages 124-125 of “Solyanik-Krassa K.V. Axisymmetric Problem of the Theory of Elasticity. – M.: Stroyizdat. 1987.”
Note 2: The calculations were performed for meshes refined by a factor of 2 and 4 (4x4 models) to study the convergence of the method. The symmetry planes were taken into account. The maximum design model contained:
- 280576 solid twenty-node isoparametric elements of type 37 (parallelepiped);
- 25600 solid fifteen-node isoparametric elements of type 35 (triangular prism).
Number of nodes in the design model – 1222501.
Comparison of solutions:
|
Thickness |
Value |
Point |
SCAD |
Deviation (%) |
|
|---|---|---|---|---|---|
|
4х4 |
1х1 |
||||
|
4m |
w(mm) |
(0,0,2) |
-0.04534 |
-0.04538 |
0.09 |
|
(0,0,0) |
-0.0454 |
-0.0454 |
– |
||
|
(0,0,-2) |
-0.04374 |
-0.04364 |
0.23 |
||
|
σr=σθ (kPa) |
(0,0,2) |
-33.6603 |
-33.78 |
0.36 |
|
|
(0,0,0) |
-1.5683 |
-1.5547 |
0.87 |
||
|
(0,0,-2) |
30.527 |
30.62 |
0.30 |
||
|
σz (kPa) |
(0,0,2) |
-10.0062 |
-10.16 |
1.36 |
|
|
(0,0,0) |
-5.0037 |
-5.0742 |
1.41 |
||
|
(0,0,-2) |
0.00326 |
-0.05 |
– |
||
|
6m |
w |
(0,0,3) |
-0.02108 |
-0.02112 |
0.19 |
|
(0,0,0) |
-0.01995 |
-0.01994 |
0.05 |
||
|
(0,0,-3) |
-0.01852 |
-0.01851 |
0.05 |
||
|
σr=σθ (kPa) |
(0,0,3) |
-17.373 |
-17.557 |
1.06 |
|
|
(0,0,0) |
-1.5213 |
-1.5149 |
0.42 |
||
|
(0,0,-3) |
14.3485 |
14.4884 |
0.98 |
||
|
σz (kPa) |
(0,0,3) |
-10.0006 |
-9.797 |
2.03 |
|
|
(0,0,0) |
-5.0367 |
-5.0694 |
0.65 |
||
|
(0,0,-3) |
0.0028 |
0.0434 |
– |
||
