Spatial Hinged Bar System Subjected to a Concentrated Force
Objective: Determination of the stress state in the elements of a spatial hinged-bar system subjected to a concentrated force.
Initial data file: CS01_v11.3.spr
Problem formulation: Three bars of the spatial system are connected by hinges in a common node (4) and are simply supported in the opposite nodes (1, 2, 3). Support nodes are arranged in one horizontal plane, the common node lies outside this plane and is loaded with a vertical concentrated force P. Determine longitudinal forces N in each bar.
References: F. P. Beer, E. R. Johnston Jr., D. F. Mazurek, P. J. Cornwell, E. R. Eisenberg, Vector Mechanics for Engineers, Statics and Dynamics, New York, McGraw-Hill Co., 1962, p. 47.
Initial data:
| E = 3.0·107 Pa | - elastic modulus, |
| A = 1.0 m2 | - cross-sectional area of the bars; |
| P = 50 N | - value of the concentrated force. |
Finite element model: Design model ‑ spatial hinged bar system, 3 bar elements of type 4. Boundary conditions in the support nodes are provided by imposing constraints in the directions of the degrees of freedom: X, Y, Z. Number of nodes in the design model – 4.
Coordinates of nodes:
|
Node |
X (m) |
Y (m) |
Z (m) |
|---|---|---|---|
|
1 |
0.0 |
0.0 |
0.0 |
|
2 |
0.0 |
72.0 |
0.0 |
|
3 |
96.0 |
0.0 |
0.0 |
|
4 |
48.0 |
24.0 |
-72.0 |
Results in SCAD
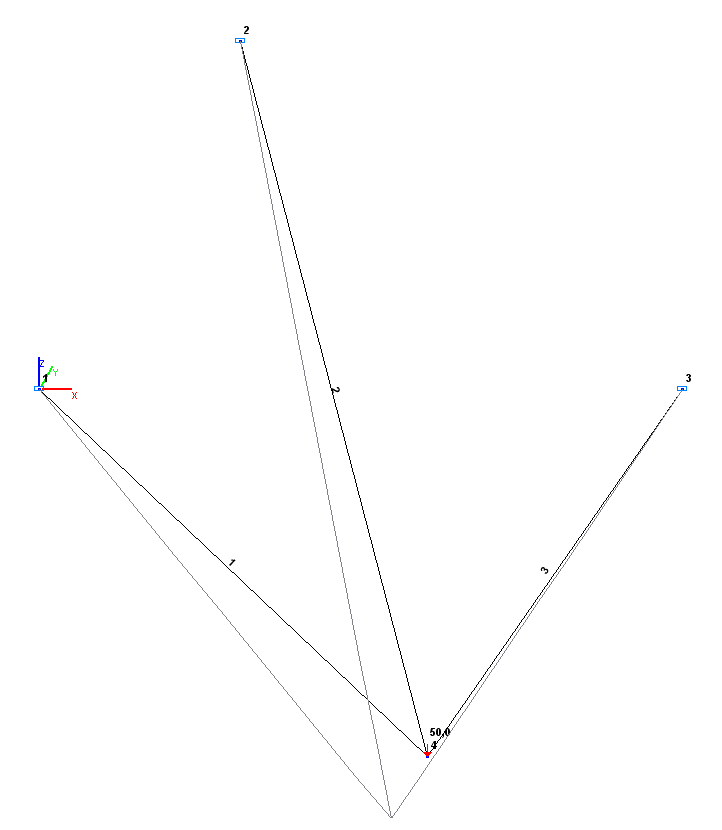
Design and deformed models
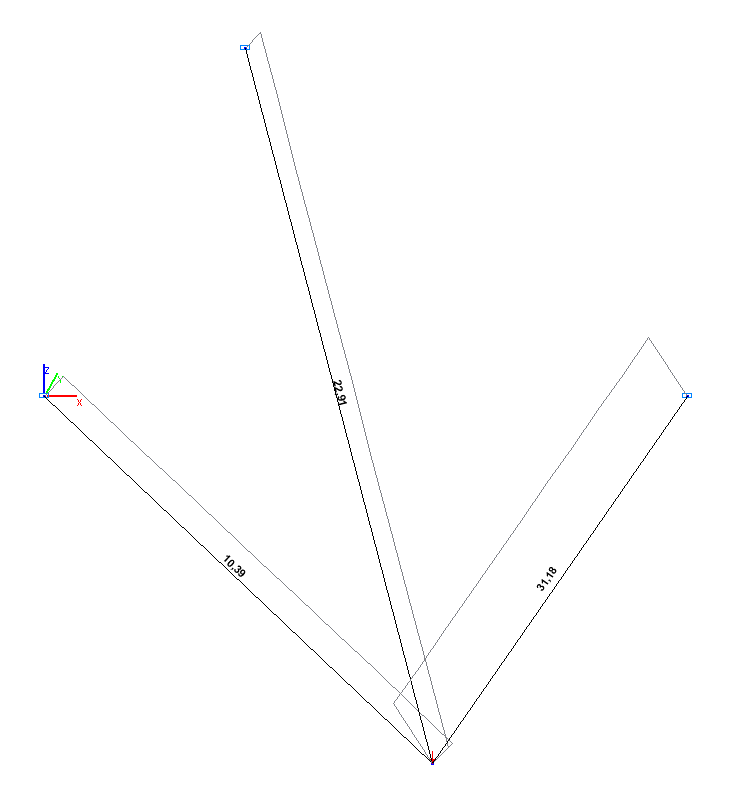Longitudinal force diagram N (N)
Comparison of solutions:
Values of longitudinal forces N (N)
|
Bar (nodes) |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
1 (1-4) |
10.39 |
10.39 |
0.00 |
|
2 (2-4) |
22.91 |
22.91 |
0.00 |
|
3 (3-4) |
31.18 |
31.18 |
0.00 |
Notes: In the analytical solution, the longitudinal forces N in the elements of the spatial hinged-bar system subjected to a concentrated load are determined according to the following formulas:
\[ N_{1} =-\frac{P\cdot \left( {x_{3} \cdot y_{2} -x_{3} \cdot y_{4} -x_{4} \cdot y_{2} } \right)\cdot \sqrt {x_{4}^{2}+y_{4}^{2}+z_{4}^{2}} }{x_{3} \cdot y_{2} \cdot z_{4} }; \] \[ N_{2} =-\frac{P\cdot y_{4} \cdot \sqrt {x_{4}^{2}+\left( {y_{2} -y_{4} } \right)^{2}+z_{4}^{2}} }{y_{2} \cdot z_{4} }; \] \[ N_{3} =-\frac{P\cdot x_{4} \cdot \sqrt {\left( {x_{3} -x_{4} } \right)^{2}+y_{4}^{2}+z_{4}^{2}} }{x_{3} \cdot z_{4} }. \]