Simply Supported Beam with a Distributed Mass Subjected to a Uniformly Distributed Instantaneous Pulse (Impact of a Beam with Immovable Supports)
Objective: Determination of the stress-strain of a simply supported beam with a distributed mass subjected to a uniformly distributed instantaneous pulse.
Initial data file: DIN_B_IL.spr, Diagram_DIN_B_IL.txt
Problem formulation: The simply supported beam of constant cross-section with the uniformly distributed mass μ is subjected to the instantaneous transverse pulse S uniformly distributed over the entire span L (impacts the immovable supports at a speed v0 = S / μ). Determine the natural oscillation modes and natural frequencies p of the simply supported beam, as well as the deflection η and the bending moment M in the cross-section in the middle of the beam span with time.
References: Rabinovich I.M., Sinitsyn A.P., Luzhin O.V., Terenin V.M., Analysis of Structures Subject to Pulse Actions, Moscow, Stroyizdat, 1970, p. 83.
S.D. Ponomarev, V.L. Biederman, K.K. Likharev, V.M. Makushin, N.N. Malinin, V.I. Feodos’yev, Fundamentals of Modern Methods for Strength Analysis in Mechanical Engineering. Dynamic Analysis. Stability. Creep. Moscow, Mashgiz, 1952, p. 364.
Initial data:
| E = 3.0·106 tf/m2 | - elastic modulus; |
| ν = 0.2 | - Poisson’s ratio; |
| b = 0.4 m | - width of the rectangular cross-section of the beam; |
| h = 0.8 m | - height of the rectangular cross-section of the beam; |
| L = 8.0 m | - beam span length; |
| γ = 2.5 tf/m3 | - specific weight of the beam material; |
| S = 0.8· tf∙s/м | - value of the uniformly distributed instantaneous pulse; |
| g = 10.00 m/s2 | - gravitational acceleration; |
| μ = 2.5·0.4·0.8/10.0 = 0.08 tf∙s2/m2 | - value of the uniformly distributed mass of the beam; |
| I = 0.4·(0.8)3/12 = 0.017067 m4 | - cross-sectional moment of inertia of the beam. |
Finite element model: Design model – grade beam / plate, 32 bar elements of type 3. Boundary conditions of the simply supported ends of the beam are provided by imposing constraints in the direction of the degree of freedom Z. The dimensional stability of the design model is provided by imposing a constraint in the node of the cross-section along the symmetry axis of the beam in the direction of the degree of freedom UX. The distributed mass is specified by transforming the static load from the self-weight of the beam μ·g.
The calculation is performed in two stages: first the natural oscillation modes and natural frequencies p are determined by the modal analysis, and then the deflections η in the cross-section in the middle of the beam span with time are determined by the direct integration of the equations of motion method. The action of the uniformly distributed instantaneous transverse pulse is described by the graph of the load variation with time and is given in the form of nodal forces acting along the Z axis of the global coordinate system with the scale factor equal to the length of the bar finite element l / n = 0.25 m (n is the number of finite elements in the design model), and the delay time 0.0 s. Intervals between the time points of the load variation graph are equal to Δtint = 0.00001 s and correspond to the integration step. When plotting the graph the pulse action is taken with a linear shape function, force value P = S· Δtint = 80000 tf and duration Δtint = 0.00001 s. The duration of the process is equal to t = 0.05094 s, which corresponds to the value of the fundamental period T1. Critical damping ratios for the 1-st and 2-nd natural frequencies are taken with the minimum value ξ = 0.0001. The conversion factor for the added static loading is equal to k = 0.981 (mass generation). Number of nodes in the design model – 33. The modal integration method is used in the calculation. The determination of the natural oscillation modes and natural frequencies is performed by the method of subspace iteration. The matrix of concentrated masses is used in the calculation.
Results in SCAD


Design model
















1-st ─ 16-th natural oscillation modes
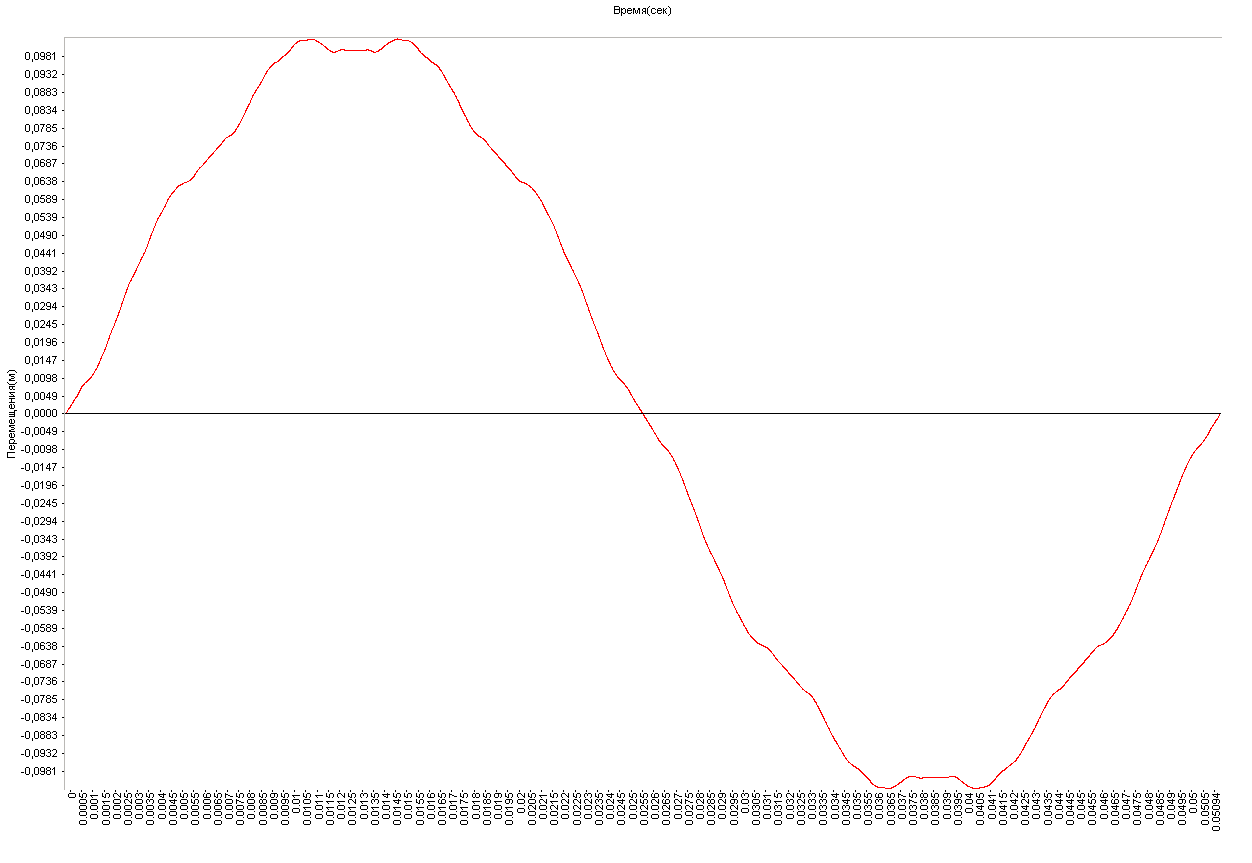
Graph of the variation of the deflection η in the cross-section in the middle of the beam span with time (m)




Amplitude values of the deflection η in the cross-section in the middle of the beam span and the deformed models at the respective time points (m)
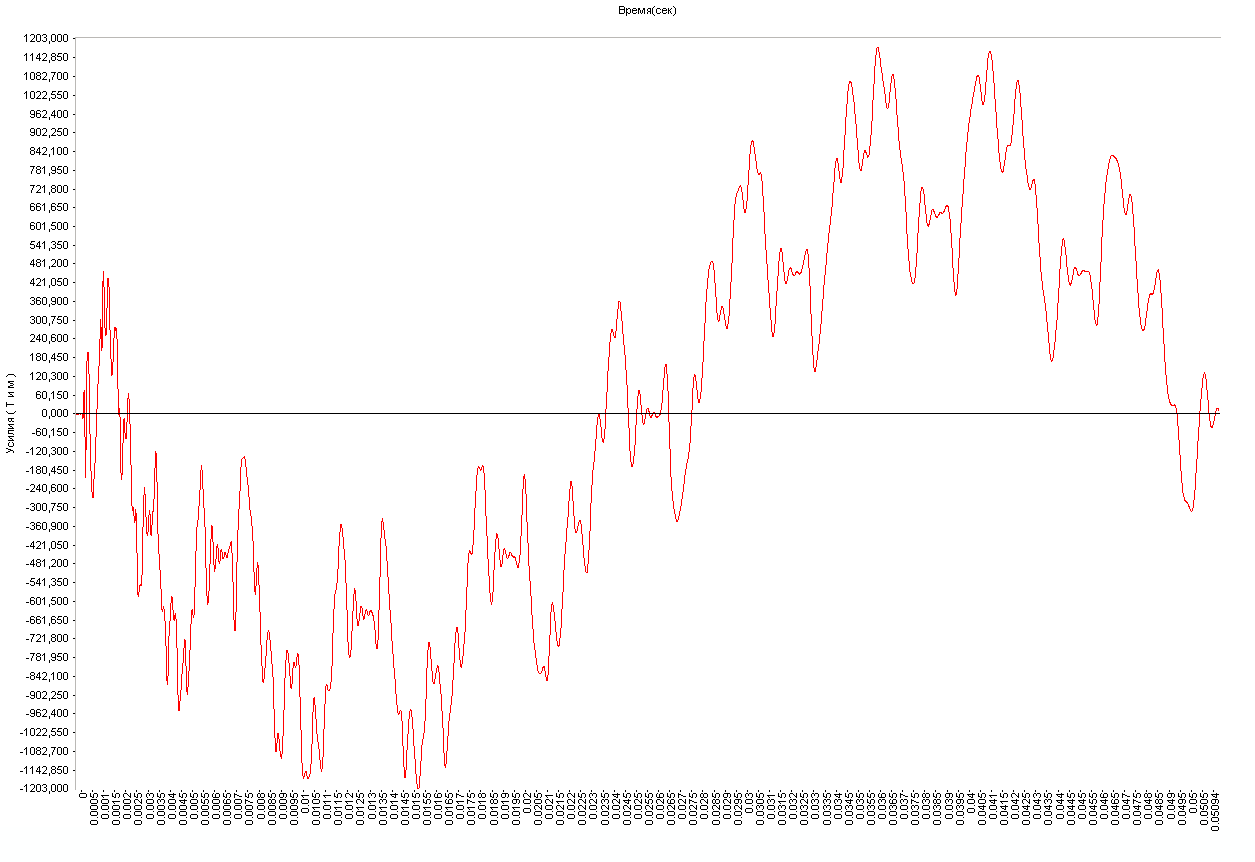
Graph of the variation of the bending moment M in the cross-section in the middle of the beam span with time (tm·m)


Amplitude values of the bending moment M in the cross-section in the middle of the beam span (tm·m)
Comparison of solutions:
Natural frequencies p, rad/s
|
Oscillation mode |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
1 |
123.370 |
123.370 |
0.00 |
|
2 |
493.480 |
493.480 |
0.00 |
|
3 |
1110.330 |
1110.325 |
0.00 |
|
4 |
1973.921 |
1973.887 |
0.00 |
|
5 |
3084.251 |
3084.120 |
0.00 |
|
6 |
4441.322 |
4440.919 |
0.01 |
|
7 |
6045.133 |
6044.087 |
0.02 |
|
8 |
7895.684 |
7893.275 |
0.03 |
|
9 |
9992.974 |
9987.907 |
0.05 |
|
10 |
12337.005 |
12327.069 |
0.08 |
|
11 |
14927.777 |
14909.367 |
0.12 |
|
12 |
17765.288 |
17732.721 |
0.18 |
|
13 |
20849.539 |
20794.097 |
0.27 |
|
14 |
24180.531 |
24089.155 |
0.38 |
|
15 |
27758.262 |
27611.778 |
0.53 |
|
16 |
31582.734 |
31353.470 |
0.73 |
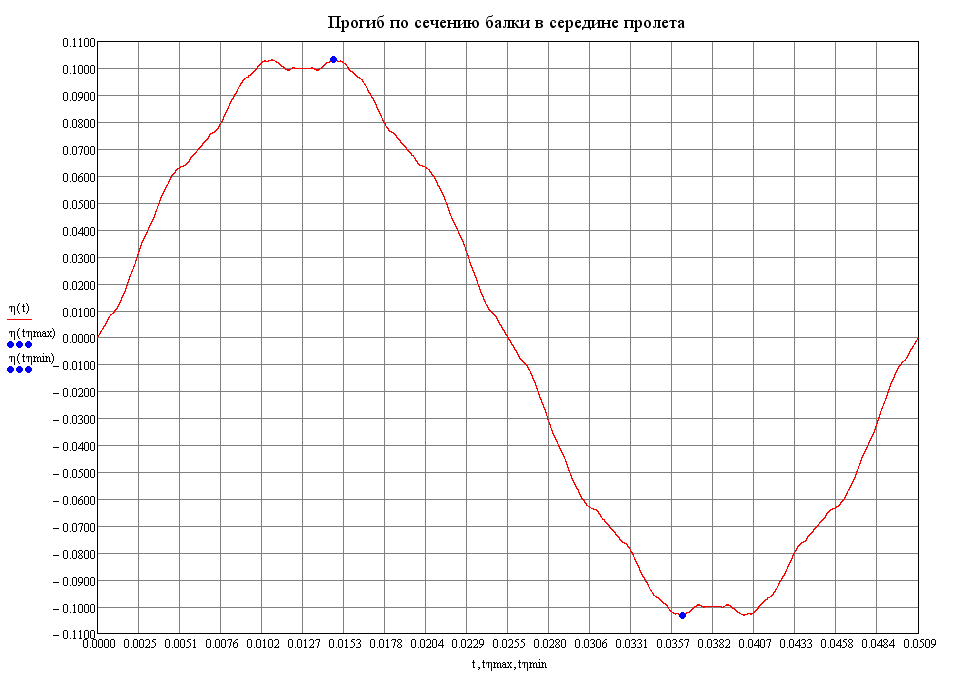
Graph of the variation of the deflection η in the cross-section in the middle of the beam span with time according to the theoretical solution (m)
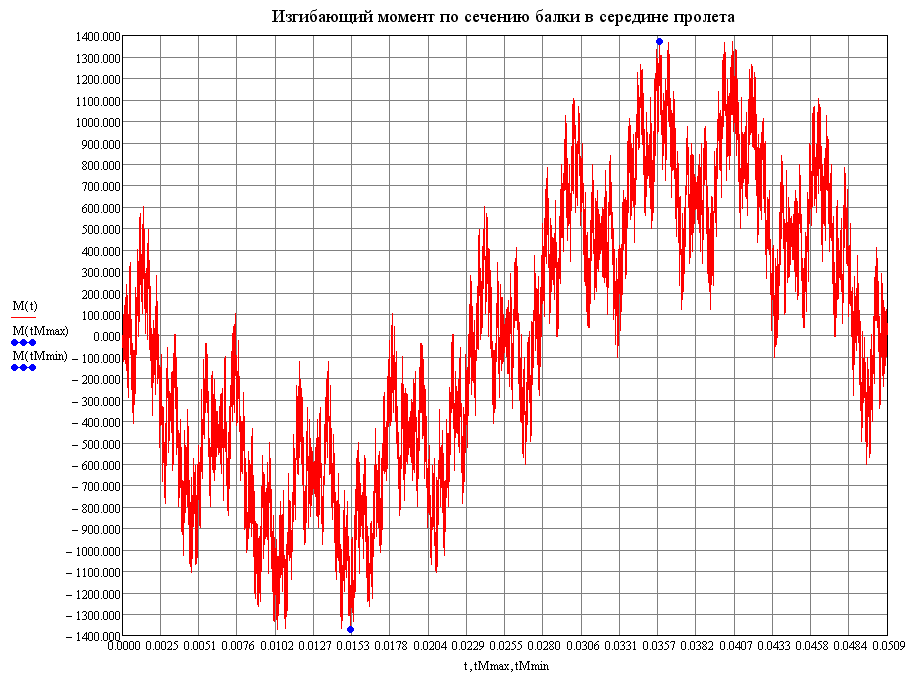
Graph of the variation of the bending moment M in the cross-section in the middle of the beam span with time according to the theoretical solution (tm·m)
Amplitude values of the deflection η in the cross-section in the middle of the beam span, m
|
Theory |
SCAD |
|||
|---|---|---|---|---|
|
Time, s |
Deflection, m |
Time, s |
Deflection, m |
Deviations, % |
|
0.014617 |
0.103196 |
0.014660 |
0.102998 |
0.19 |
|
0.036313 |
-0.103196 |
0.036330 |
-0.102825 |
0.36 |
Amplitude value of the bending moment M in the cross-section in the middle of the beam span, tf·m
|
Theory |
SCAD |
|||
|---|---|---|---|---|
|
Time, s |
Bending moment, tf·m |
Time, s |
Bending moment, tf·m |
Deviations, % |
|
0.015162 |
-1369.739 |
0.015240 |
-1203.795 |
12.12 |
|
0.035768 |
1369.739 |
0.035710 |
1177.088 |
14.06 |
Notes: In the analytical solution the natural frequencies of oscillations p of the simply supported beam are determined according to the following formula:
\[ \frac{n^{2}\cdot \pi^{2}}{l^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} , \]
where n = 1, 2, 3, 4, … – natural mode number.
In the analytical solution the deflection η and the bending moment M in the cross-section in the middle of the beam span with time are determined according to the following formula:
\[ \eta \left( t \right)=\frac{4\cdot S\cdot l^{2}}{\pi^{3}\cdot \sqrt {\mu \cdot E\cdot I} }\cdot \sum\limits_{n=1} {\left[ {\frac{\sin \left( {\frac{n\cdot \pi }{2}} \right)\cdot \sin \left( {\frac{n^{2}\cdot \pi ^{2}}{l^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)}{n^{3}}} \right]} ; \] \[ M\left( t \right)=\frac{4\cdot S}{\pi }\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot \sum\limits_{n=1} {\left[ {\frac{\sin \left( {\frac{n\cdot \pi }{2}} \right)\cdot \sin \left( {\frac{n^{2}\cdot \pi^{2}}{l^{2}}\cdot \sqrt {\frac{E\cdot I}{\mu }} \cdot t} \right)}{n}} \right]} . \]
