Cantilever Beam Subjected to a Concentrated Load

Objective: Analysis for bending in the force plane under a concentrated force without taking into account the transverse shear deformations. The values of the maximum transverse displacement, rotation angle and bending moment are checked.
Initial data file: Example_4_1.spr
Problem formulation: The cantilever beam is loaded by a concentrated force Р applied to its free end. Determine the maximum values of the transverse displacement w, rotation angle θ and bending moment М.
References: G.S. Pisarenko, A.P. Yakovlev, V.V. Matveev, Handbook on Strength of Materials. — Kiev: Naukova Dumka, 1988, p. 263.
Initial data:
| E = 2.0·1011 Pa | - elastic modulus, |
| ν = 0.3 | - Poisson’s ratio, |
| L = 3 м | - beam length; |
| I = 2.44·10-6 м4 | - cross-sectional moment of inertia; |
| Р = 5 kN | - value of the concentrated force. |
Finite element model: Design model – general type system, 10 bar elements of type 5, 11 nodes.
Results in SCAD:

Bending moment diagram М (kN·m)
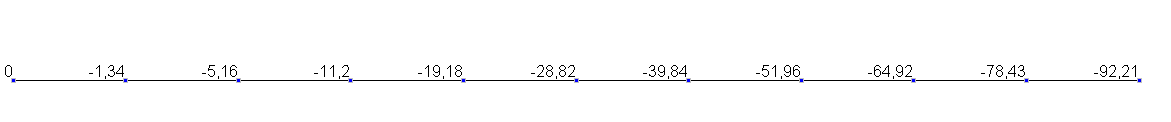
Values of transverse displacements w(mm)

Values of rotation angles θ (rad)
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|
|
Transverse displacement w, mm |
-92.21 |
-92.21 |
0.00 |
|
Rotation angle Ө, rad |
0.04611 |
0.04611 |
0.00 |
|
Bending moment М, kN·m |
-15.0 |
-15.0 |
0.00 |
Notes: In the analytical solution, the maximum values of the transverse displacement w, rotation angle θ and bending moment М are determined according to the following formulas:
\[ w=-\frac{P\cdot L^{3}}{3\cdot E\cdot I}; \quad \theta =\frac{P\cdot L^{2}}{2\cdot E\cdot I}; \quad M=-P\cdot L. \]
