Natural Oscillations of a Simply Supported Square Plate
Objective: Modal analysis of a simply supported square plate.
Initial data file: 5_2.spr
Problem formulation: Determine the natural oscillation modes and frequencies ω of the simply supported square plate with the density of the material ρ.
References: I.A. Birger, Ya.G. Panovko, Strength, Stability, Vibrations, Handbook in three volumes, Volume 3, Moscow, Mechanical engineering, 1968, p. 375.
Initial data:
| E = 2.06·108 kPa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| ρ = 7.85 t/m3 | - density of the material; |
| h = 0.01 m | - thickness of the plate; |
| a1 = 1.0 m | - long side of the plate (along the X axis of the global coordinate system); |
| a2 = 1.0 m | - short side of the plate (along the Y axis of the global coordinate system). |
Finite element model: Design model – grade beam / plate, 400 plate elements of type 20. The spacing of the finite element mesh along the sides of the plate (along the X, Y axes of the global coordinate system) is 0.05 m. Boundary conditions are provided by imposing constraints in the direction of the degree of freedom Z for the edges parallel to the X and Y axes of the global coordinate system. The distributed mass is specified by transforming the static load from the self-weight of the plate ow = γ∙h, where γ = ρ∙g = 77.01 kN/m3. Number of nodes in the design model – 441. The determination of the natural oscillation modes and natural frequencies is performed by the Lanczos method. A consistent mass matrix is used in the calculation.
Results in SCAD
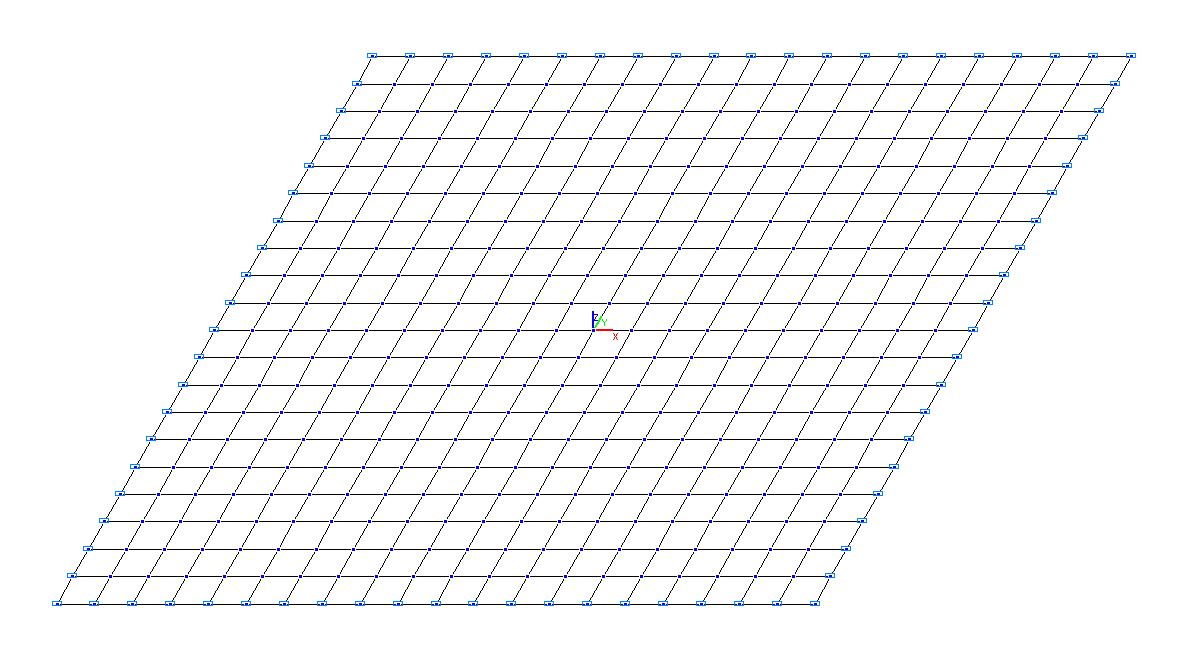
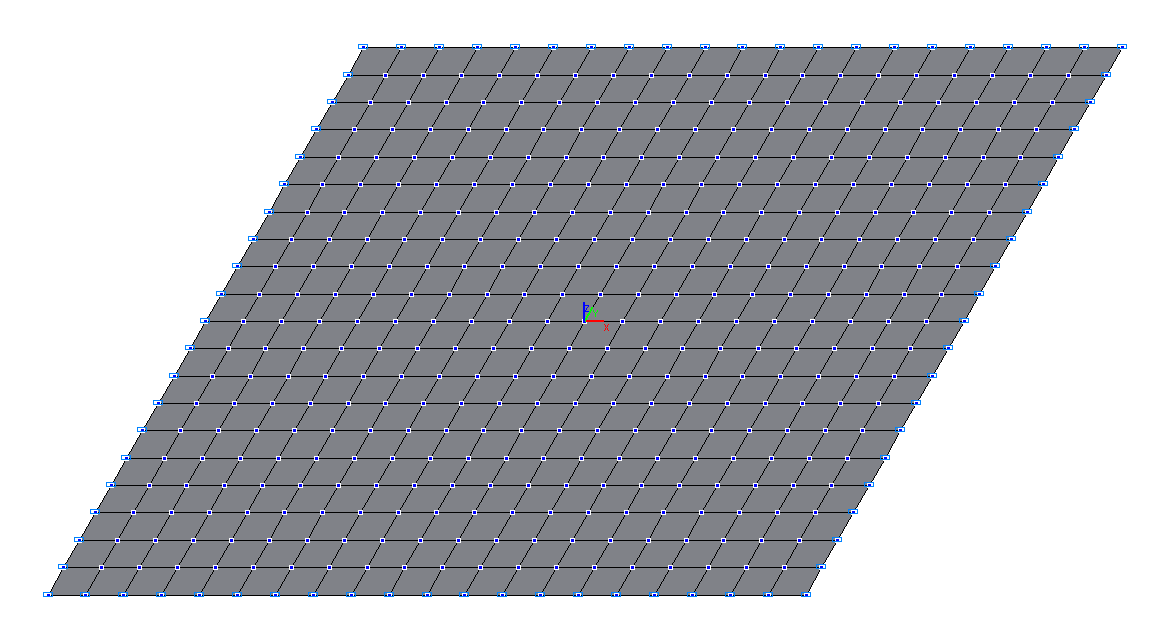
Design model
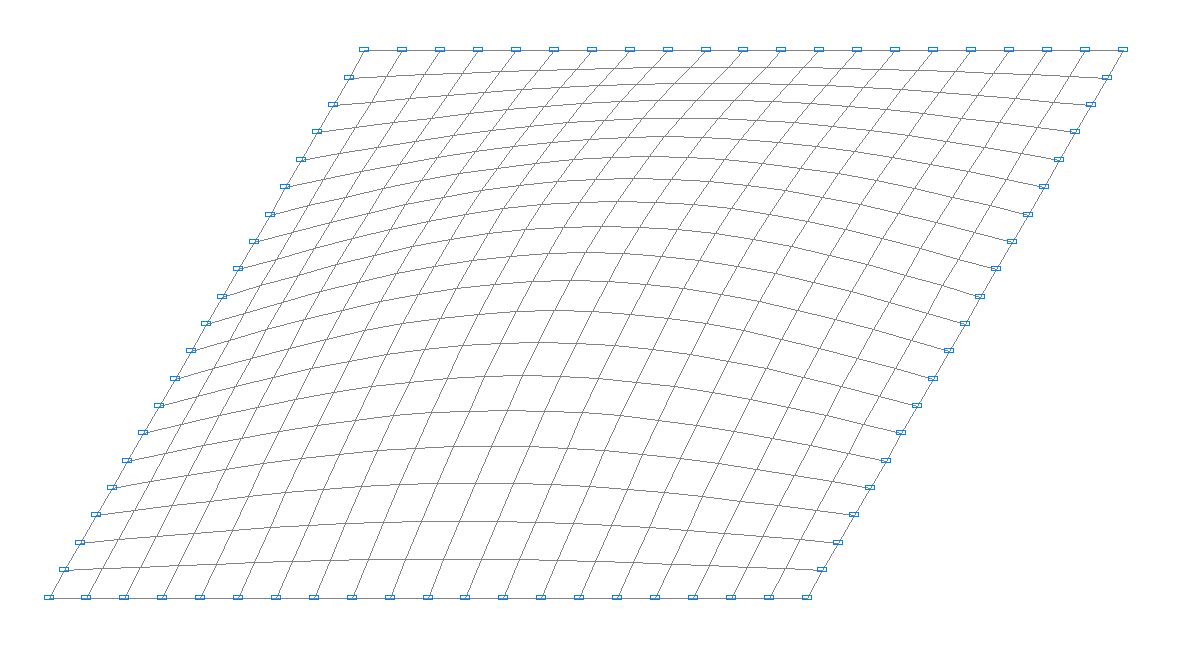


1-st natural oscillation mode
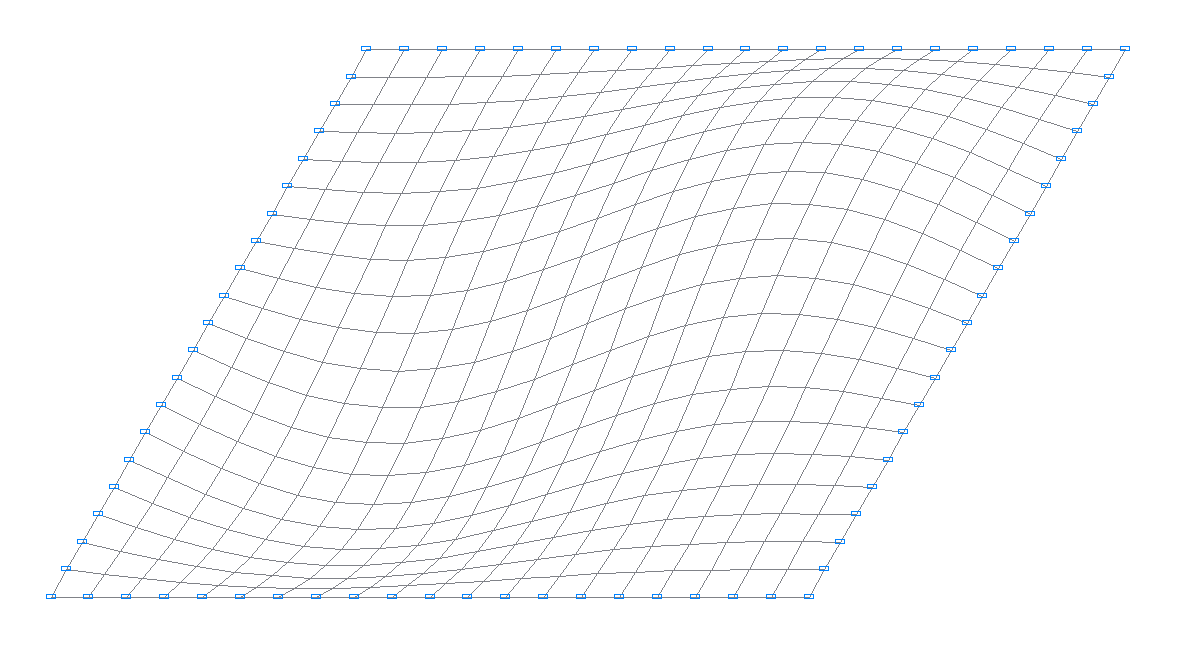
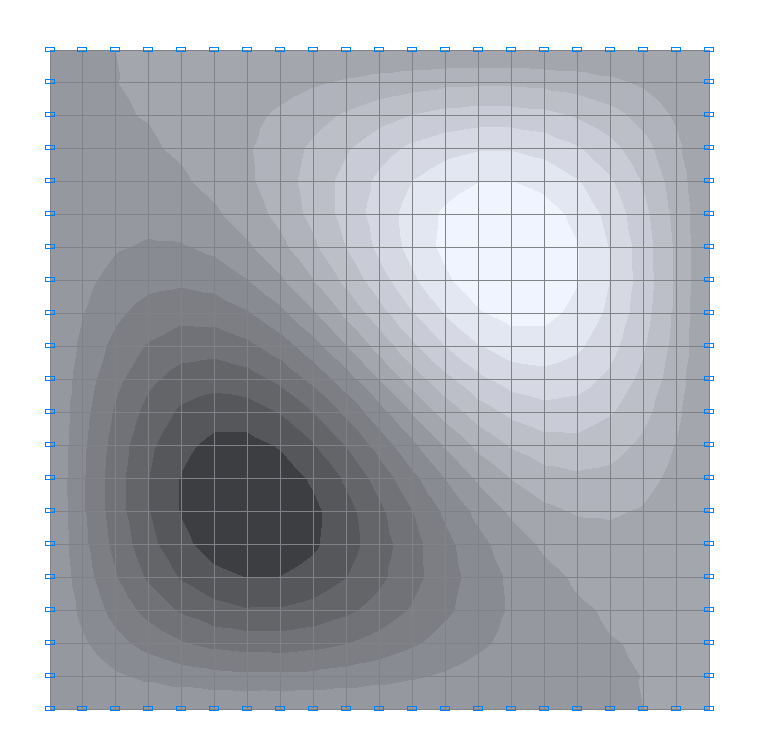

2-nd natural oscillation mode
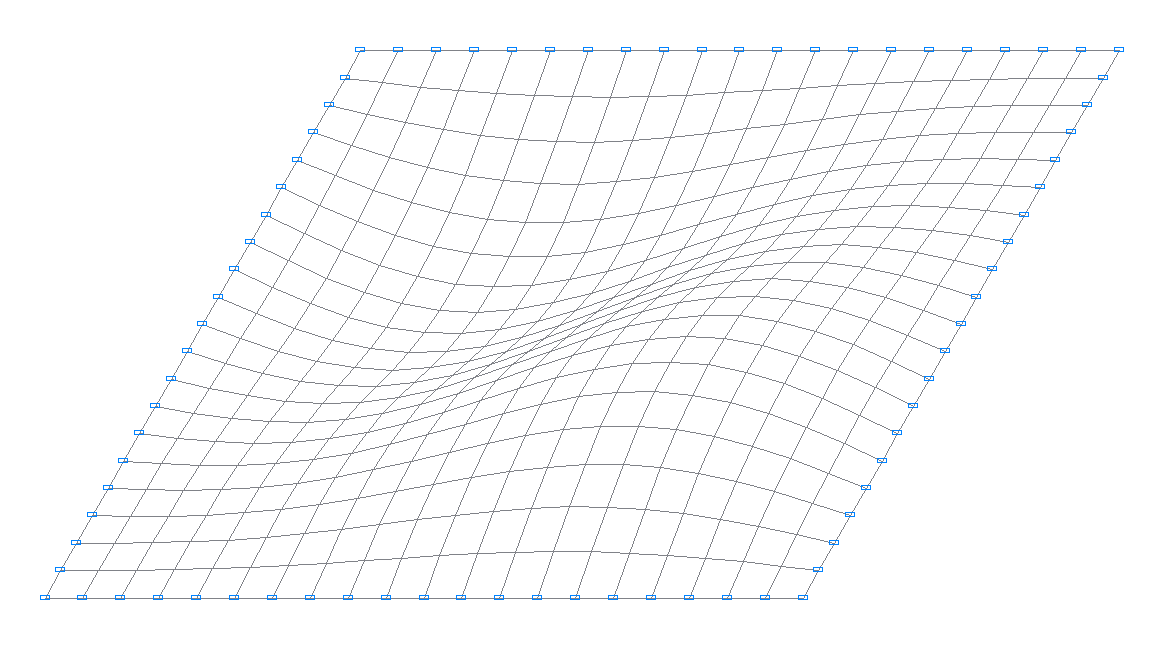
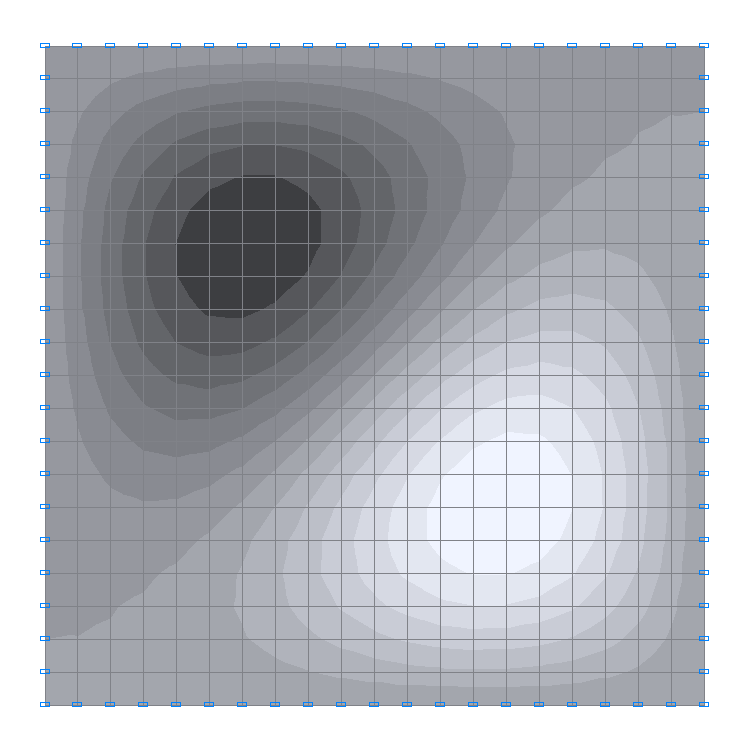

3-rd natural oscillation mode
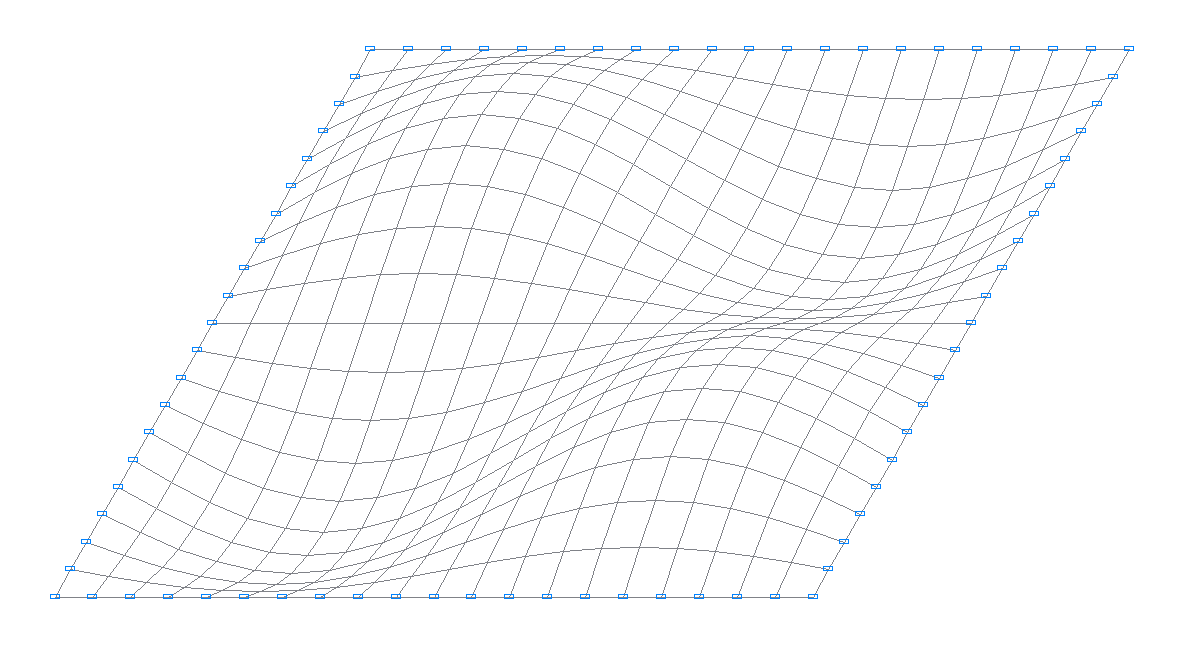


4-th natural oscillation mode
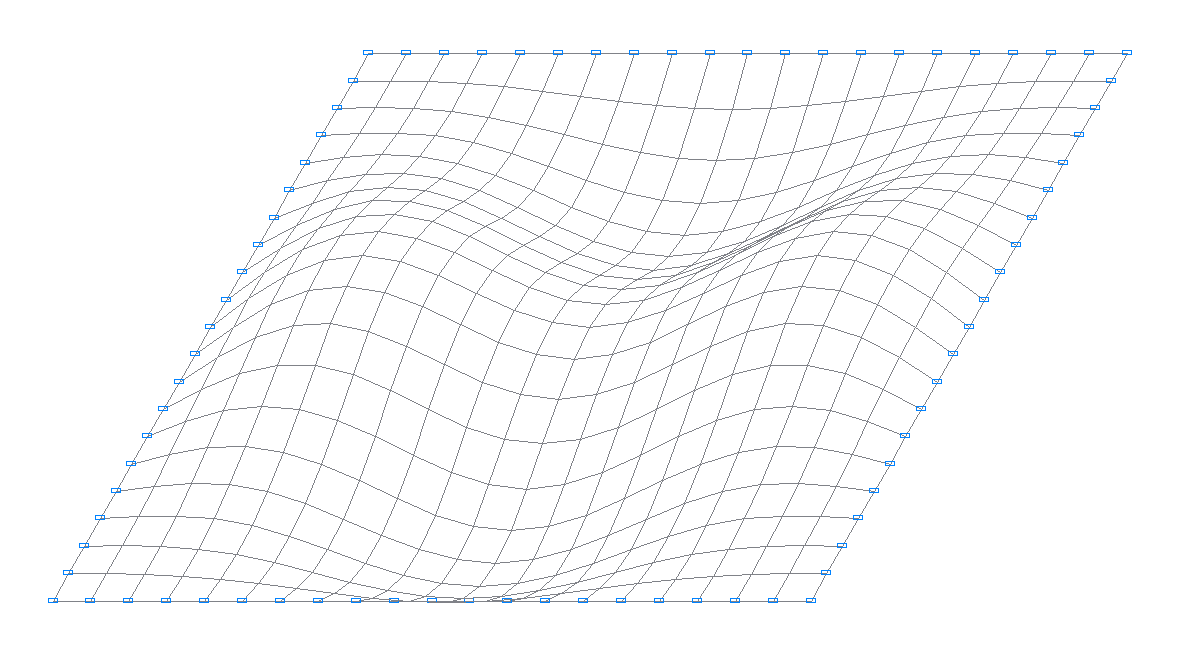
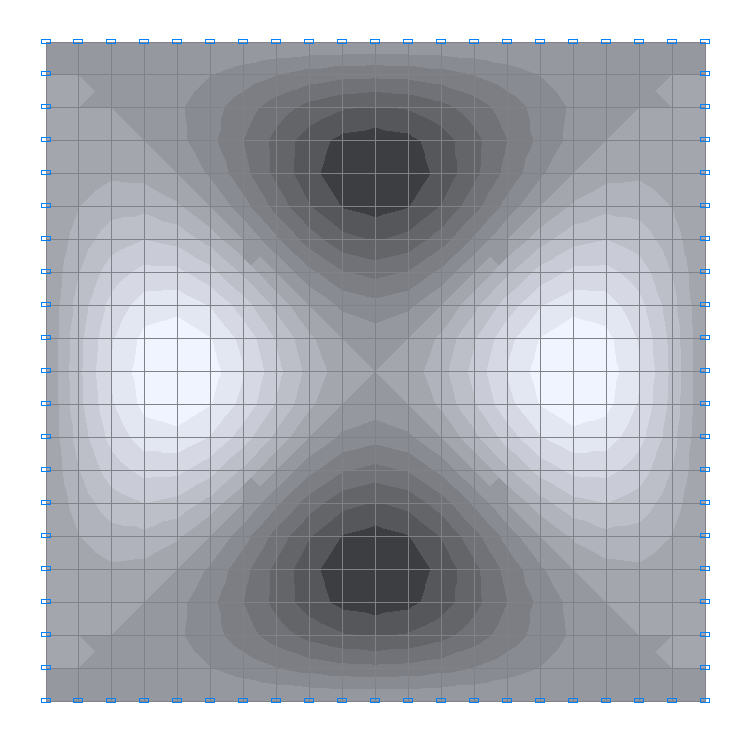

5-th natural oscillation mode
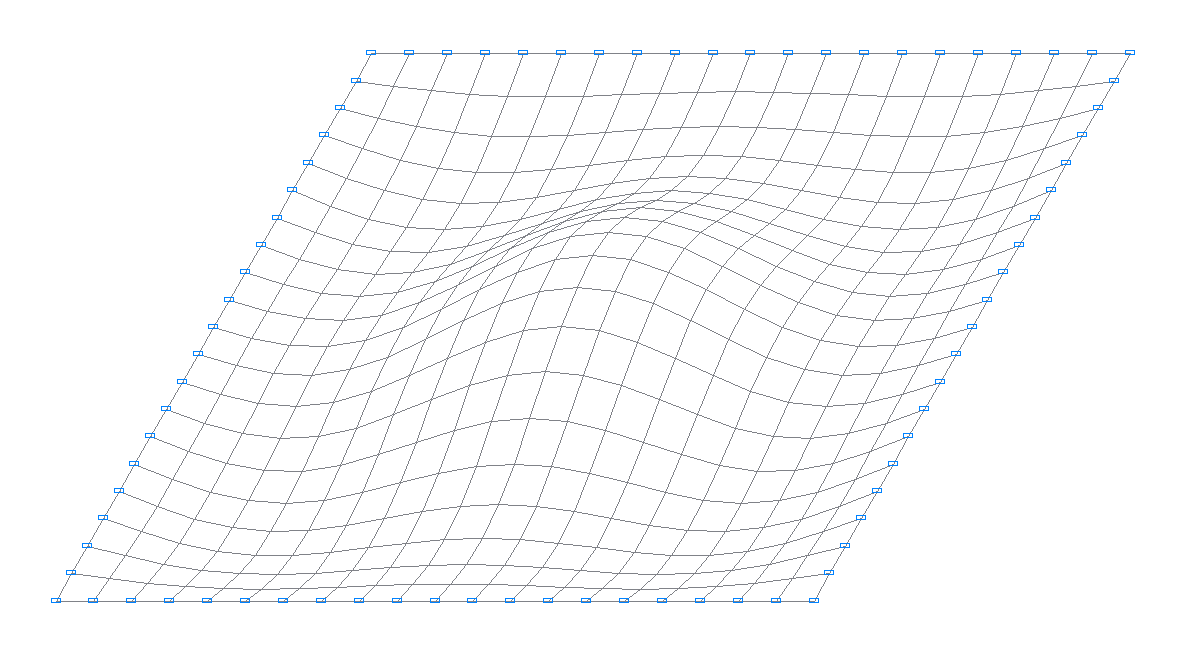


6-th natural oscillation mode
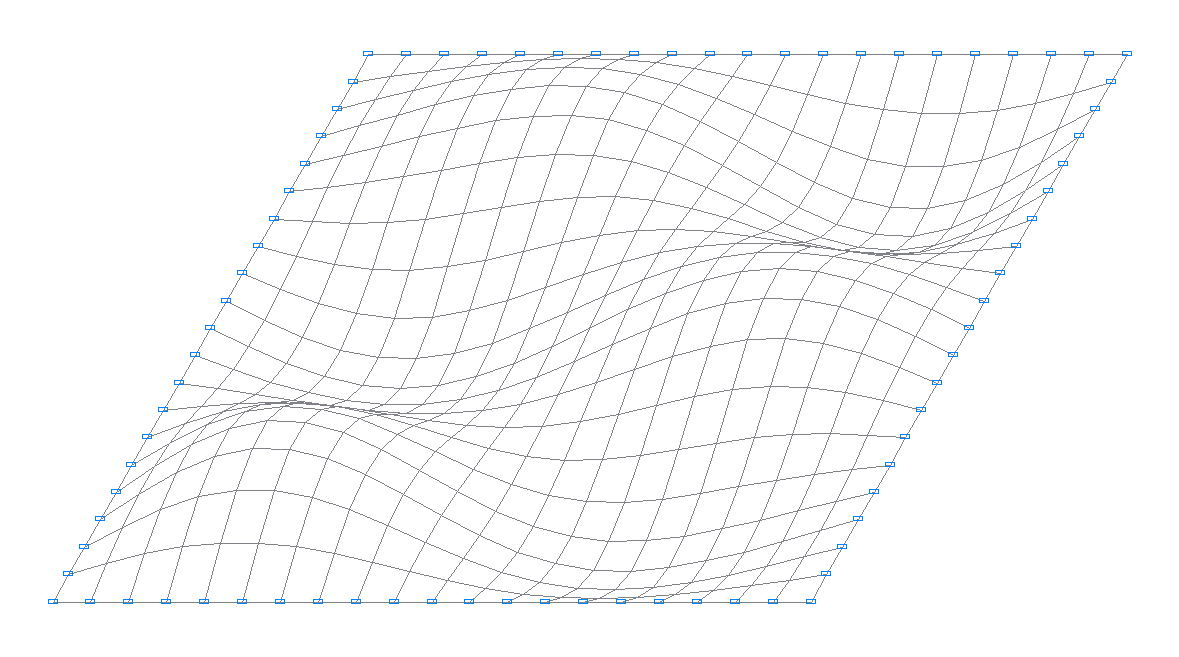
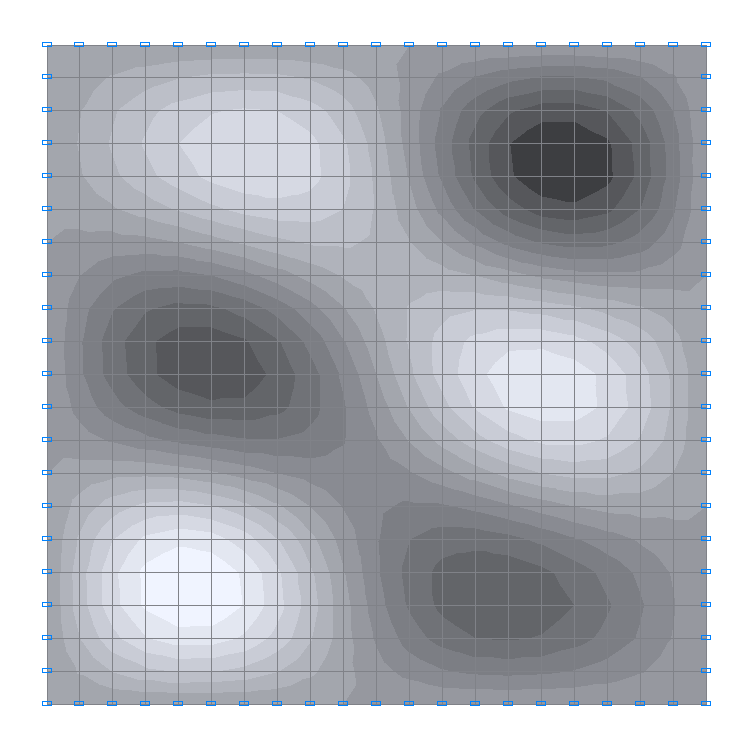

7-th natural oscillation mode
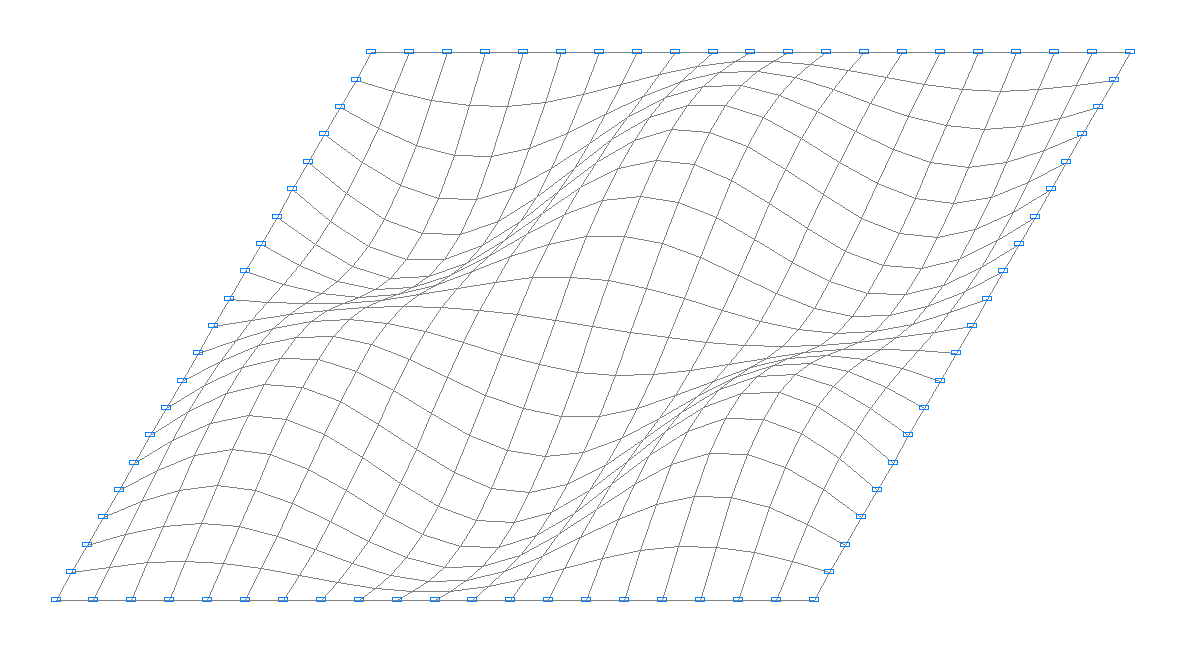
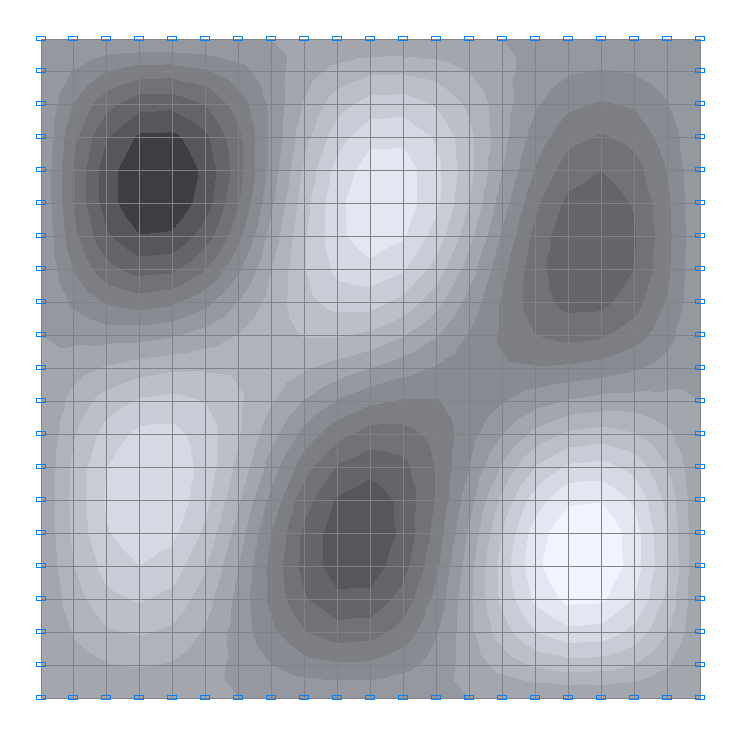

8-th natural oscillation mode
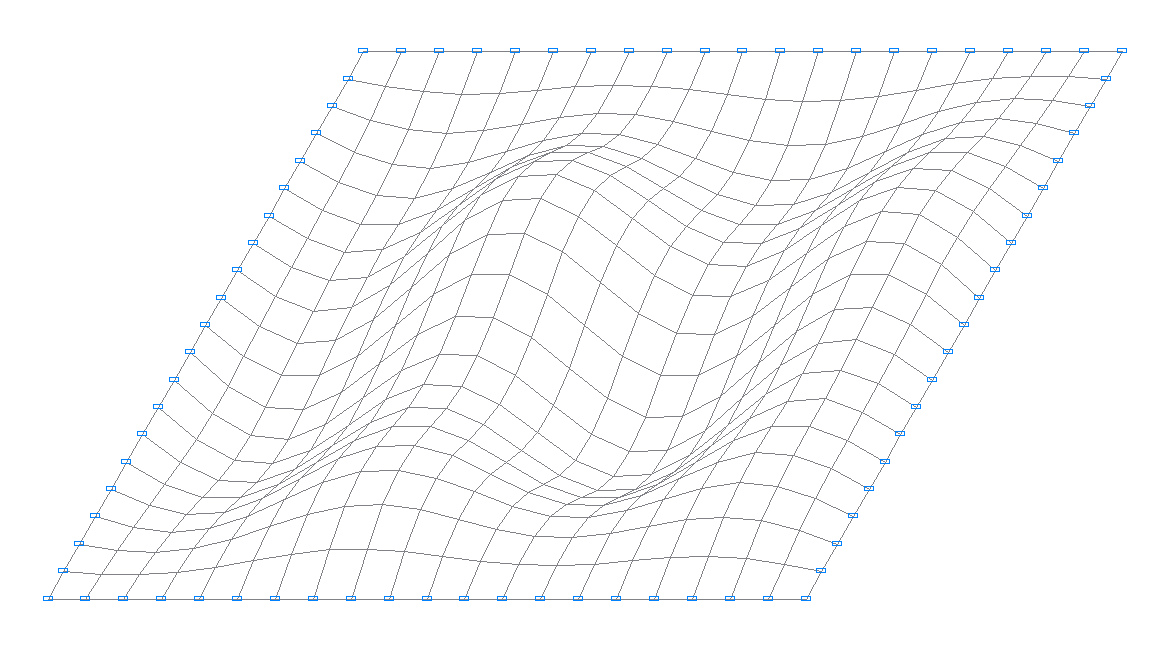


9-th natural oscillation mode
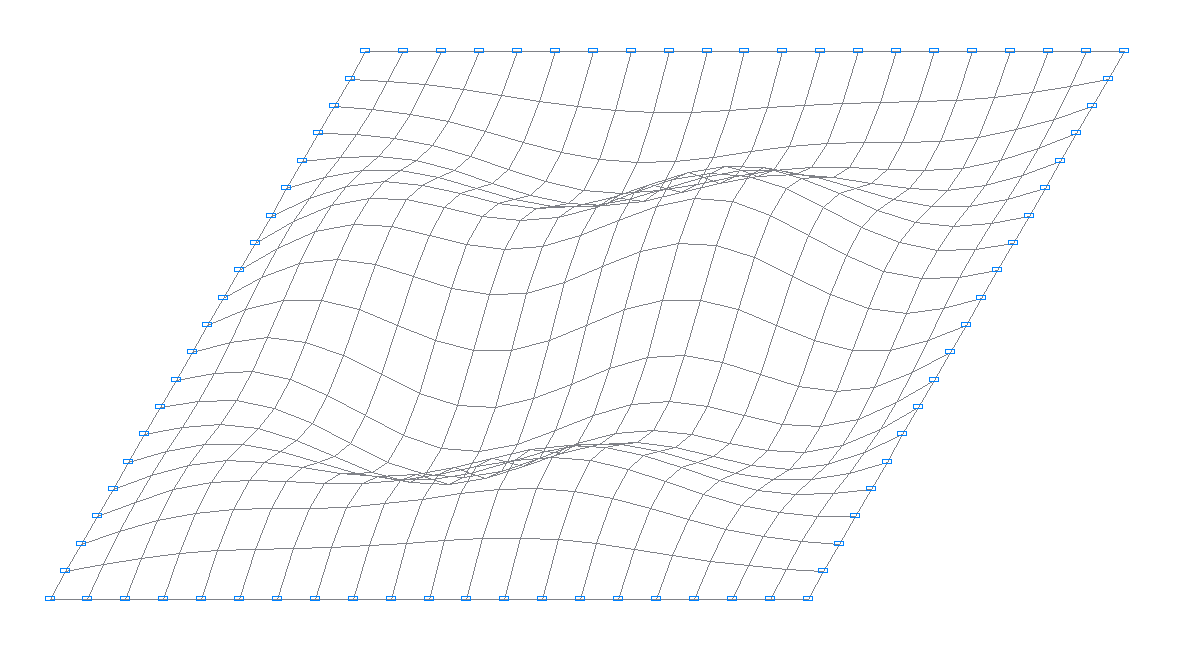


10-th natural oscillation mode
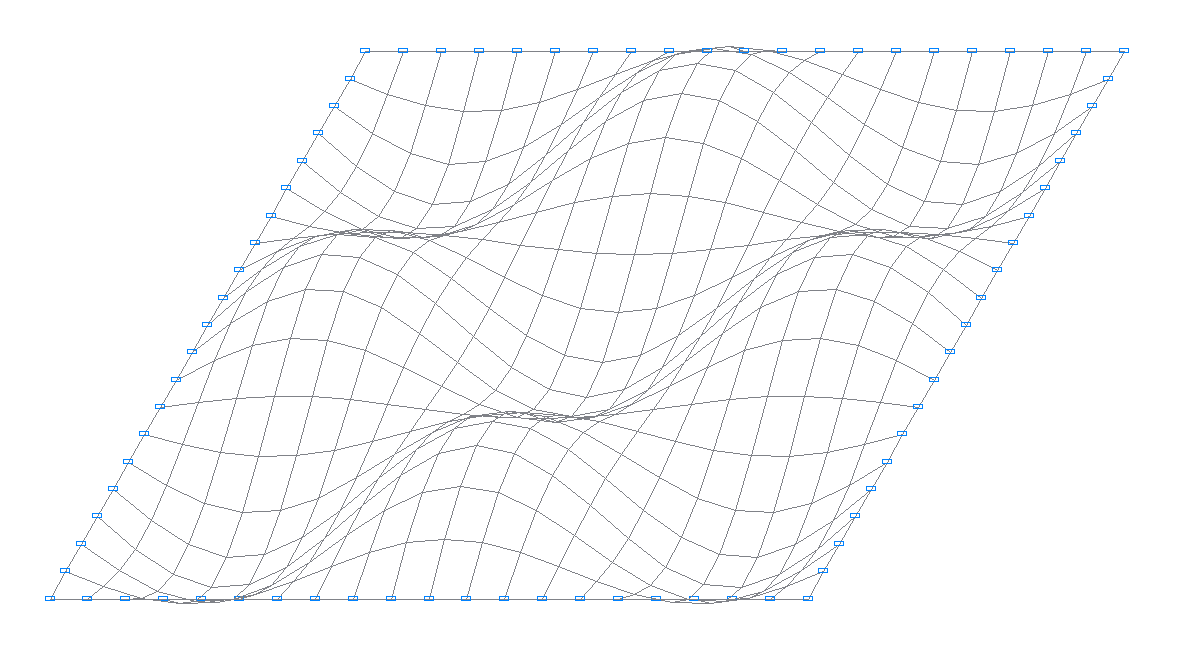


11-th natural oscillation mode
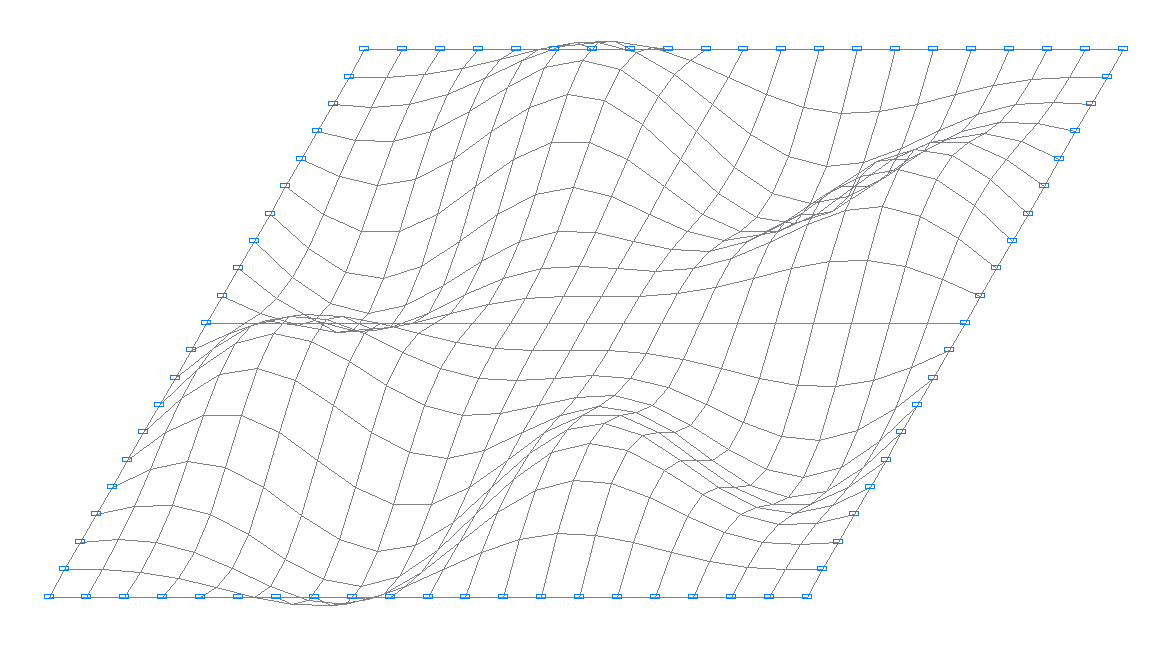


12-th natural oscillation mode
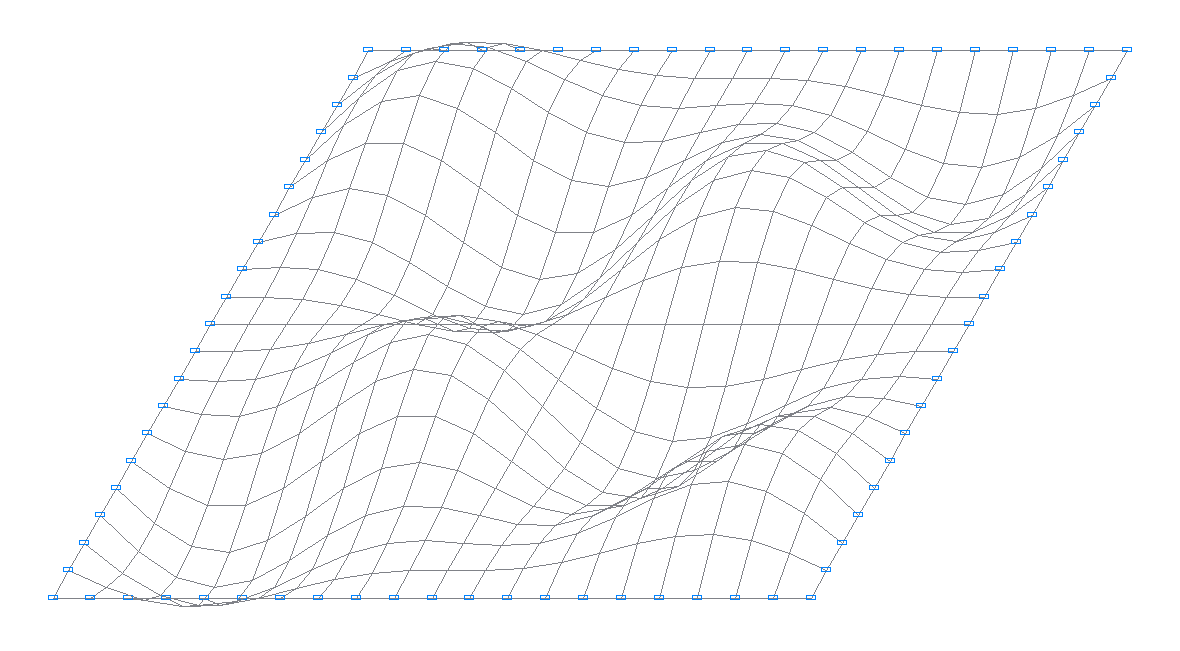


13-th natural oscillation mode
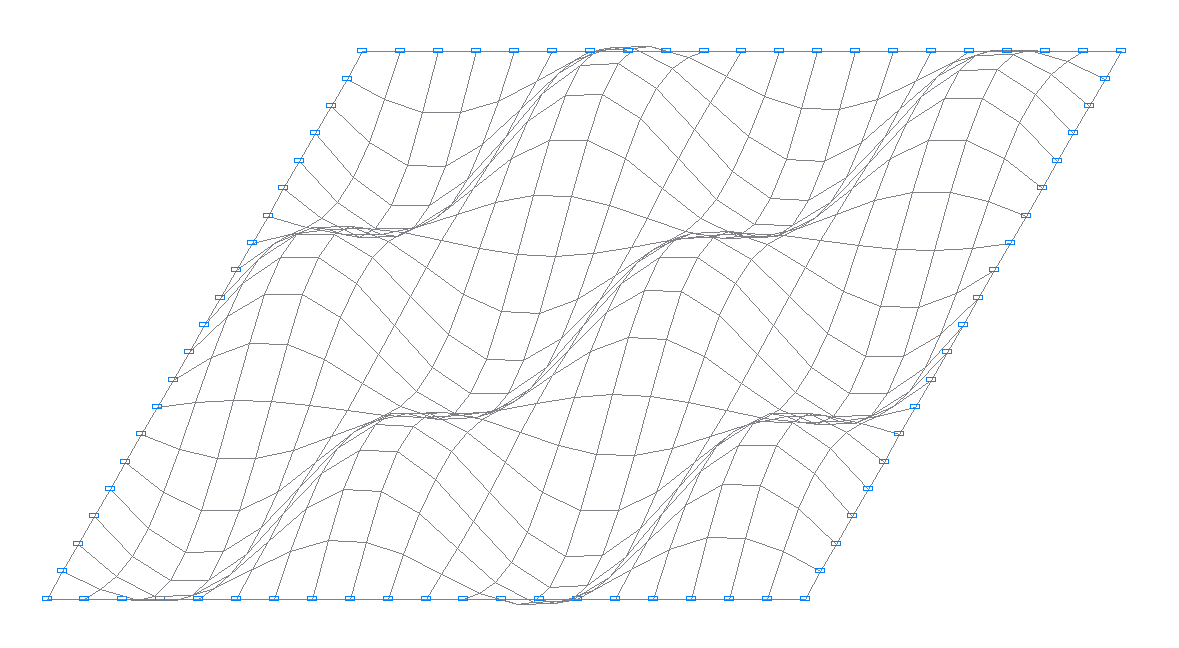


14-th natural oscillation mode
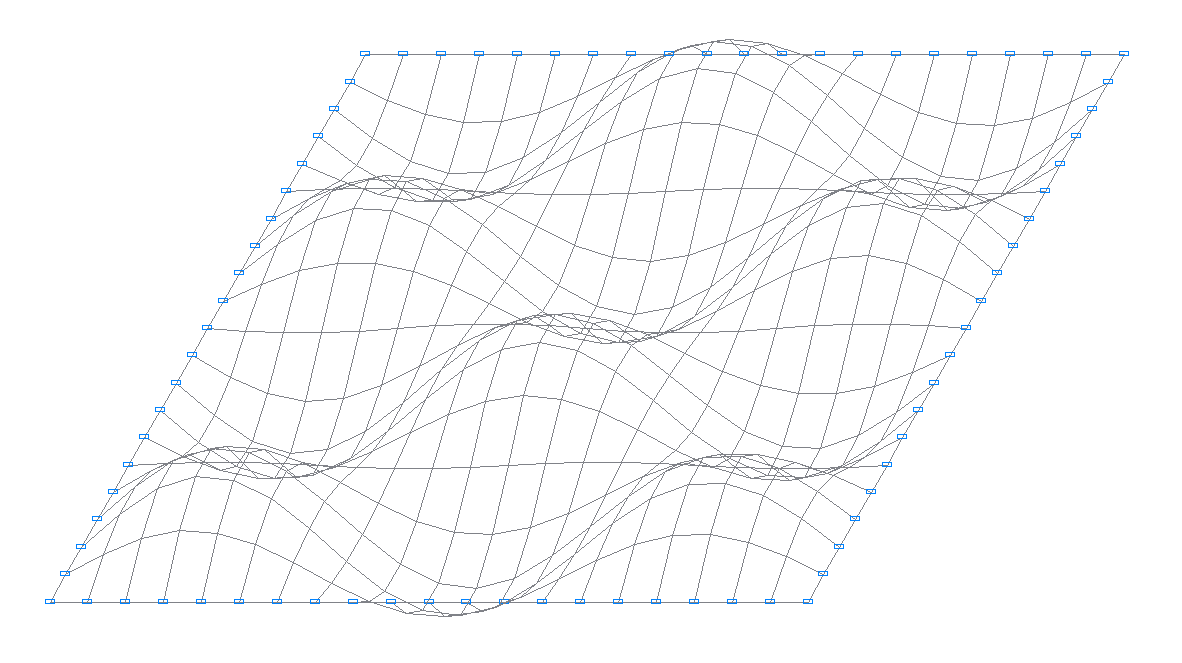

15-th natural oscillation mode
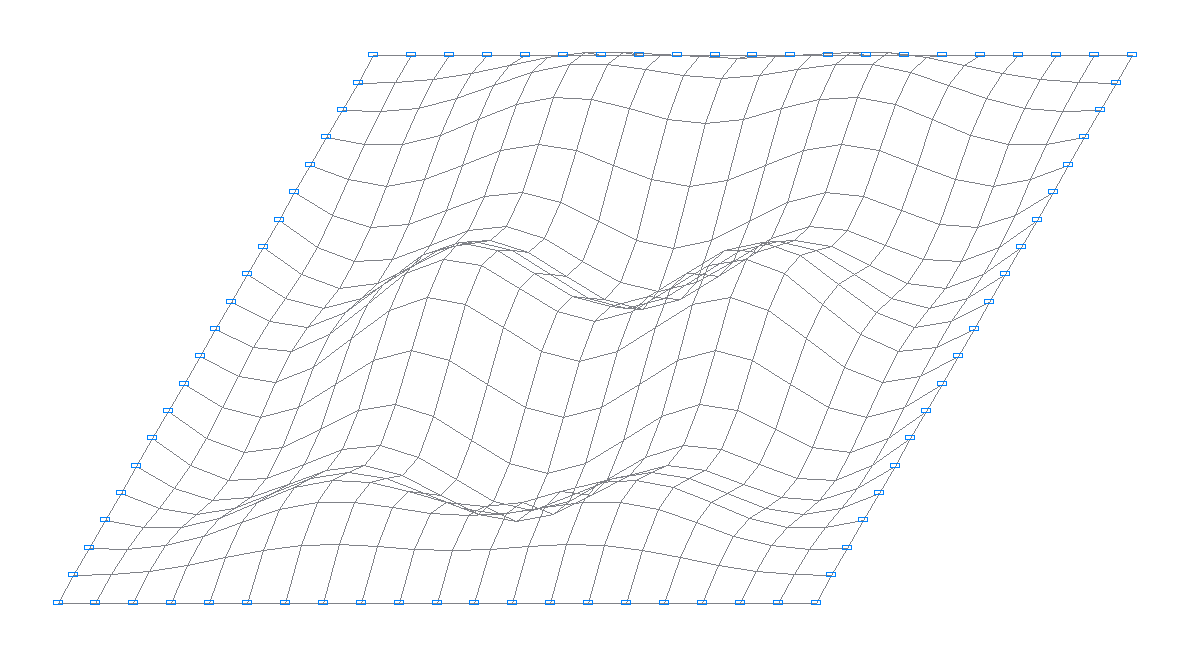


16-th natural oscillation mode
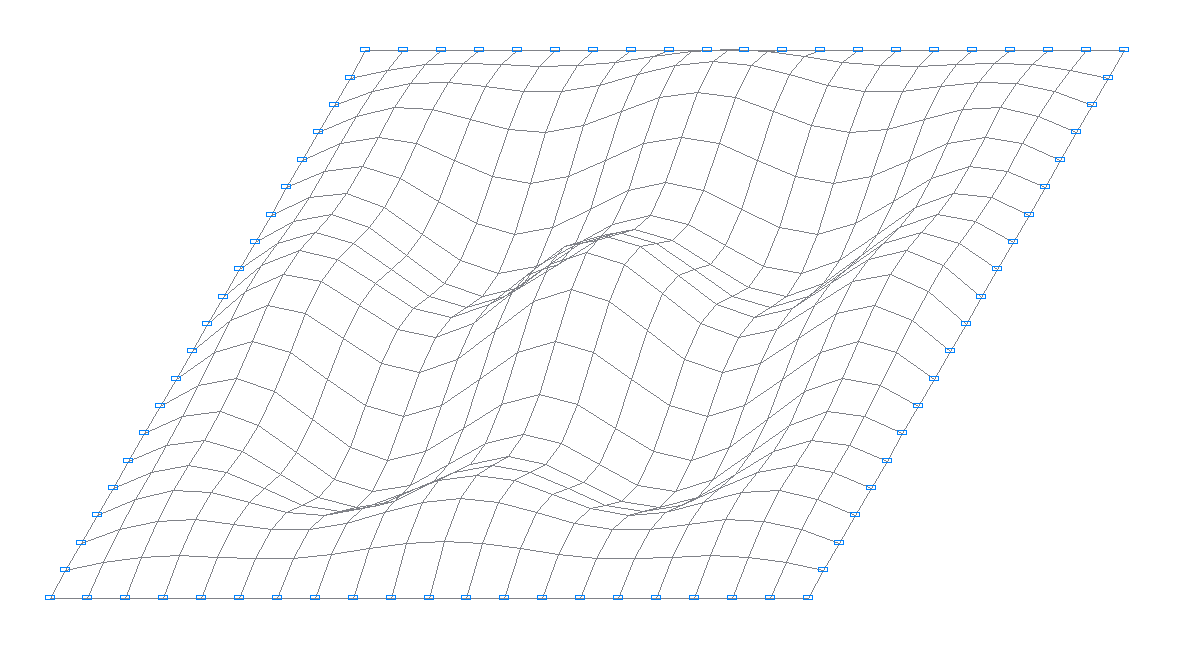
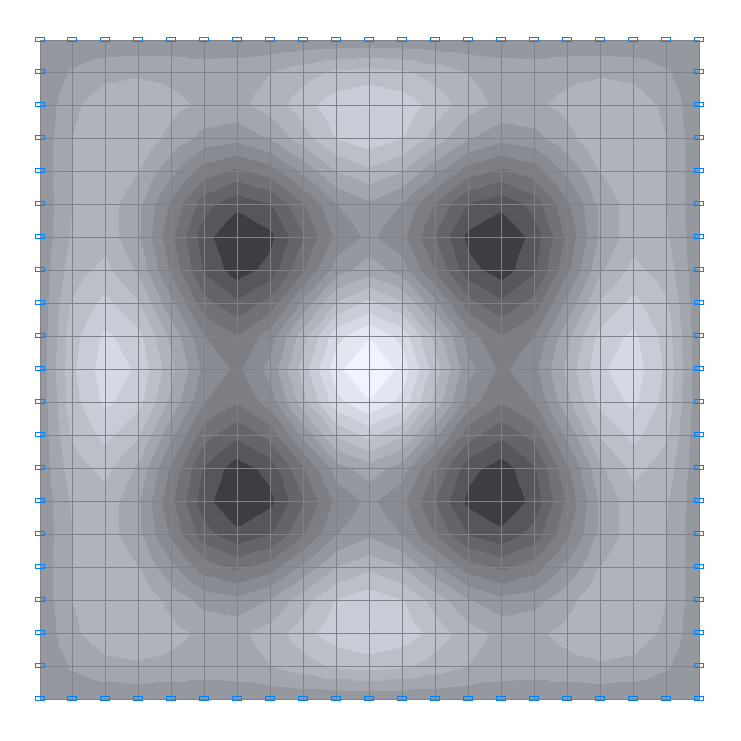
17-th natural oscillation mode

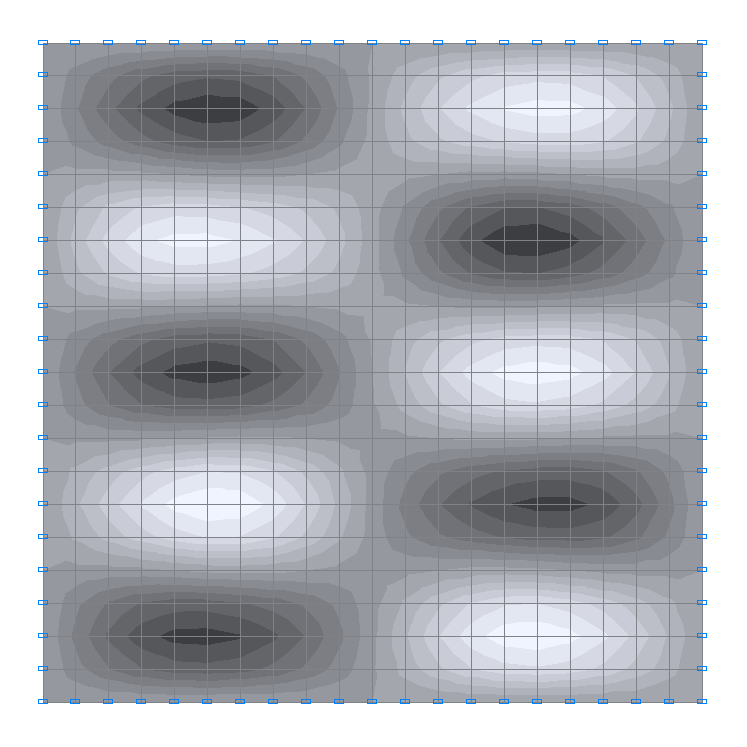

18-th natural oscillation mode
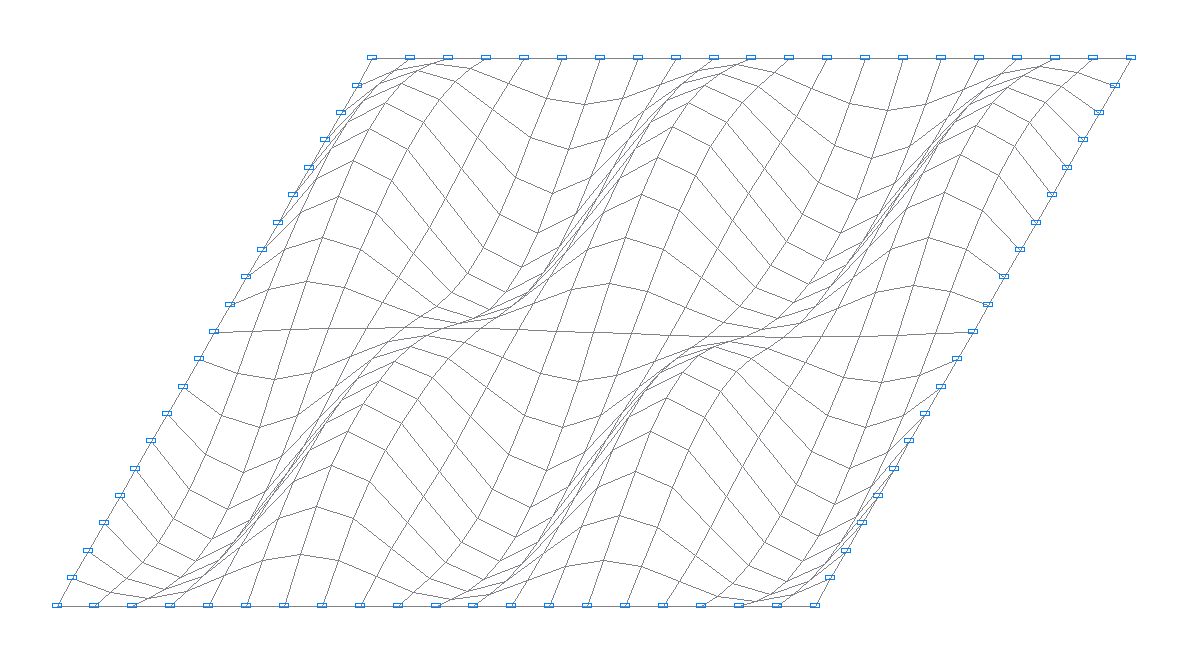
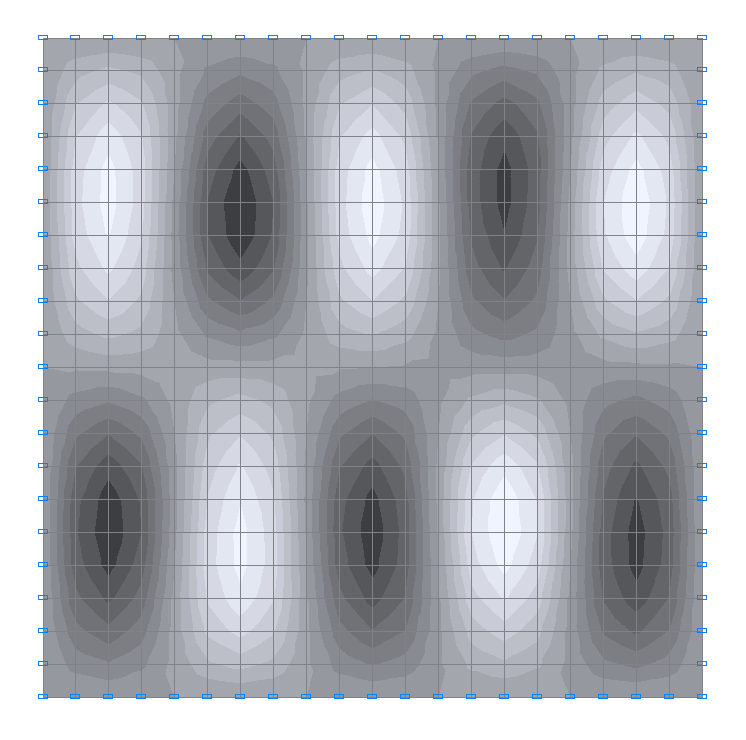

19-th natural oscillation mode



20-th natural oscillation mode
Comparison of solutions:
Natural frequencies ω, rad / s
|
Oscillation mode |
Number of half waves |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|---|
|
1 |
1, 1 |
306.0 |
306,1 |
0,05 |
|
2 |
1, 2 |
765. 0 |
765,6 |
0,08 |
|
3 |
2, 1 |
765.0 |
765,6 |
0,08 |
|
4 |
2, 2 |
1224.0 |
1226,4 |
0,19 |
|
5 |
1, 3 |
1530.0 |
1531,4 |
0,09 |
|
6 |
3, 1 |
1530.0 |
1531,4 |
0,09 |
|
7 |
2, 3 |
1989.0 |
1994,4 |
0,27 |
|
8 |
3, 2 |
1989.0 |
1994,4 |
0,27 |
|
9 |
1, 4 |
2601.0 |
2603,6 |
0,10 |
|
10 |
4, 1 |
2601.0 |
2603,6 |
0,10 |
|
11 |
3, 3 |
2754.0 |
2766,2 |
0,44 |
|
12 |
2, 4 |
3060.0 |
3069,7 |
0,32 |
|
13 |
4, 2 |
3060.0 |
3069,7 |
0,32 |
|
14 |
3, 4 |
3825.0 |
3846,8 |
0,57 |
|
15 |
4, 3 |
3825.0 |
3846,8 |
0,57 |
|
16 |
1, 5 |
3978.0 |
3982,6 |
0,12 |
|
17 |
5, 1 |
3978.0 |
3982,6 |
0,12 |
|
18 |
2, 5 |
4437.0 |
4452,7 |
0,35 |
|
19 |
5, 2 |
4437.0 |
4452,7 |
0,35 |
|
20 |
4, 4 |
4896.0 |
4934,7 |
0,79 |
Notes: In the analytical solution the natural frequencies ω of the simply supported square plate with the density of the material ρ can be determined according to the following formula:
\[\omega =\pi^{2}\cdot \left( {\frac{m_{1}^{2}}{a_{2}^{2}}+\frac{m_{2} ^{2}}{a_{2}^{2}}} \right)\cdot \left( {\frac{D}{\rho \cdot h}} \right)^{\frac{1}{2}},\quad where:\quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\mu ^{2}} \right)}\quad, \quad m_{1}, m_{2} =1,2,3, ... \]
