Natural Oscillations of a Simply Supported Circular Cylindrical Shell
Objective: Modal analysis of a simply supported circular cylindrical shell.
Initial data file: 5.8_s.spr
Problem formulation: Determine the natural oscillation modes and frequencies ω of the simply supported circular cylindrical shell with the density of the material ρ.
References: I.A. Birger, Ya.G. Panovko, Strength, Stability, Vibrations, Handbook in three volumes, Volume 3, Moscow, Mechanical engineering, 1968, p. 426.
V. L. Biderman, Theory of Mechanical Oscillations, Moscow, High School, 1980, p. 290.
Initial data:
| E = 1.96·108 kPa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| ρ = 7.70 t/m3 | - density of the material; |
| h = 0.25·10-3 m | - thickness of the cylindrical shell; |
| R = 0.076 m | - radius of the midsurface of the cylindrical shell; |
| L = 0.305 m | - length of the cylindrical shell. |
Finite element model: Design model – general type system, 6400 four-node shell elements of type 50. The spacing of the finite element mesh in the meridian direction is 4.765625·10-3 m (64 elements) and in the circumferential is 3.6º (100 elements). Boundary conditions of the simply supported edges are provided by imposing constraints in the directions of the linear displacements in their plane (degrees of freedom Y, Z). The dimensional stability of the design model is provided by imposing constraints of finite rigidity (100 elements of type 51) in the nodes of the cross-section on the symmetry plane of the cylindrical shell in the meridian direction (kx = 1.0 kN/m). The distributed mass is specified by transforming the static load from the self-weight of the cylindrical shell: ow = γ∙h, where γ = ρ∙g = 75.537 kN/m3. Number of nodes in the design model – 6500. The determination of the natural oscillation modes and natural frequencies is performed by the method of subspace iteration. The matrix of concentrated masses is used in the calculation.
Results in SCAD
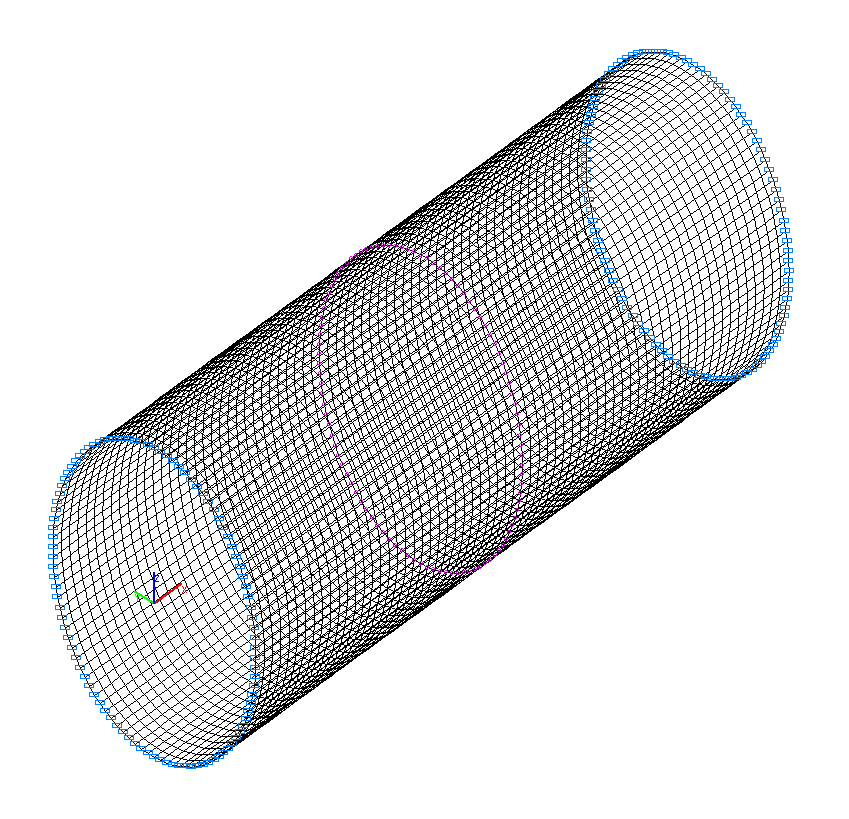
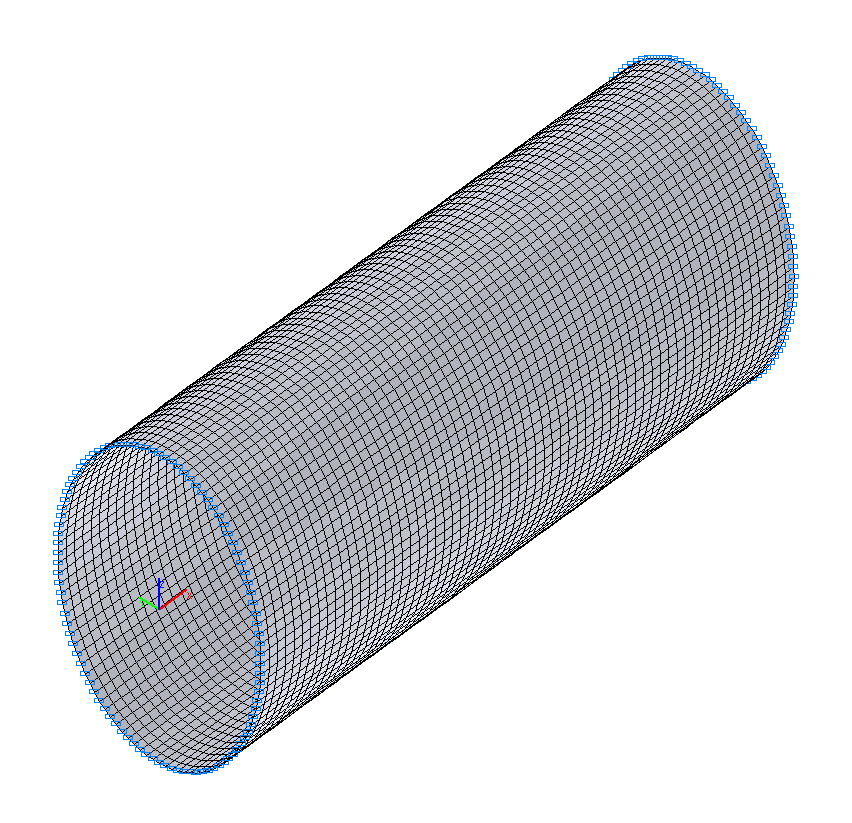
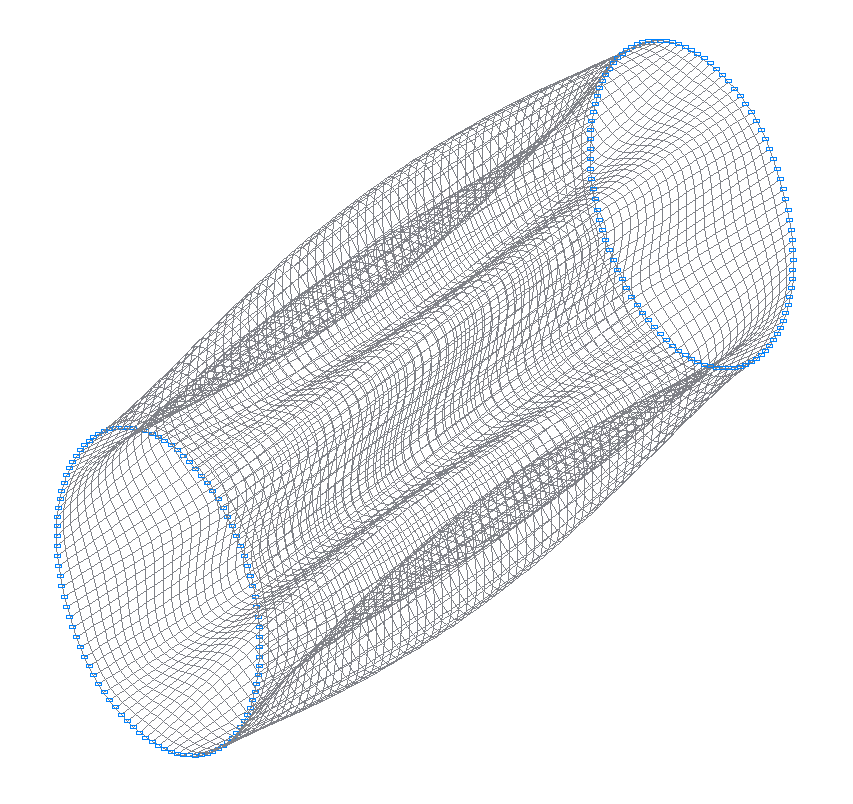
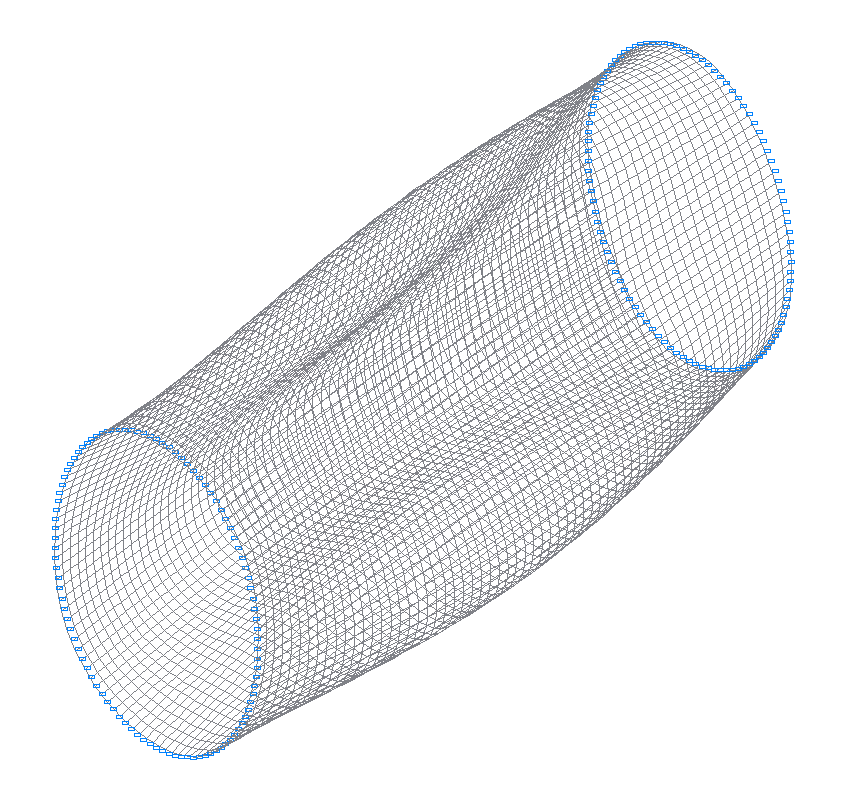
Design model
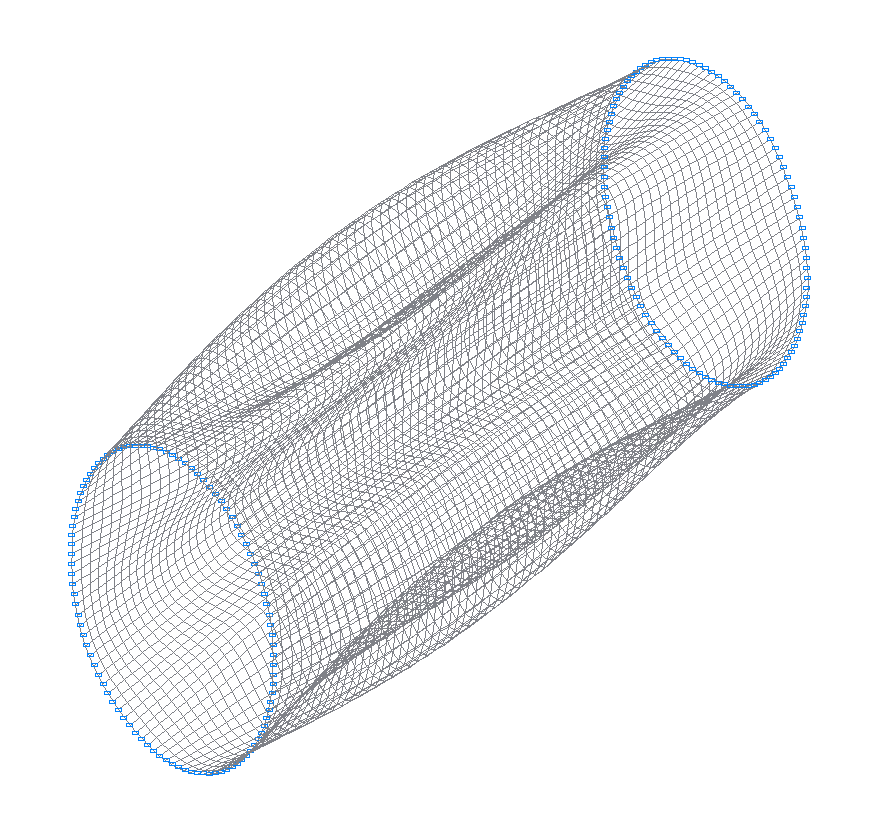


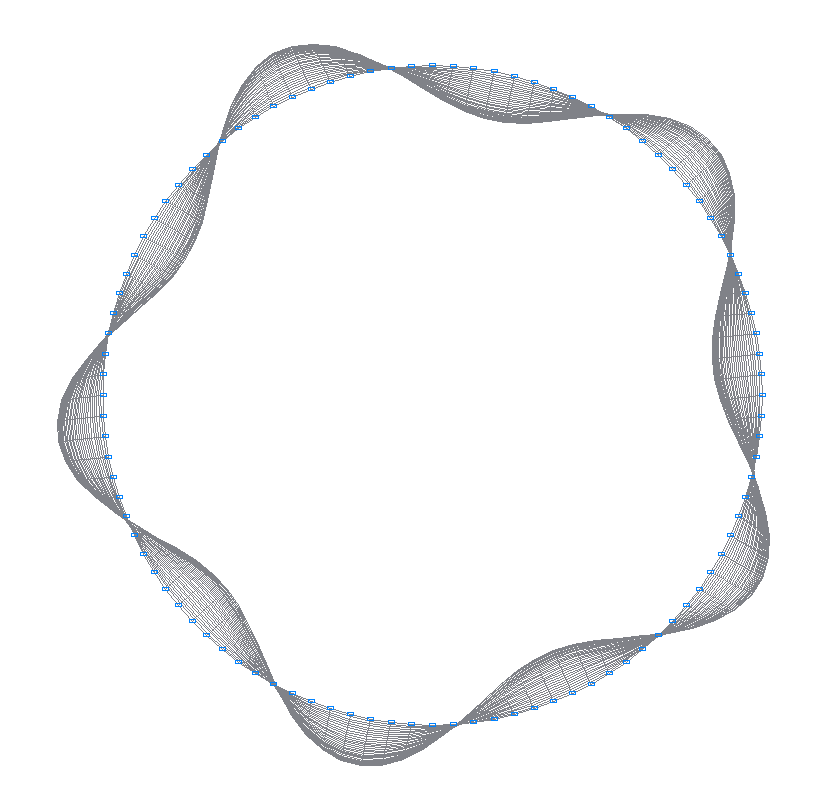
2-nd (1-st theoretical) natural oscillation mode

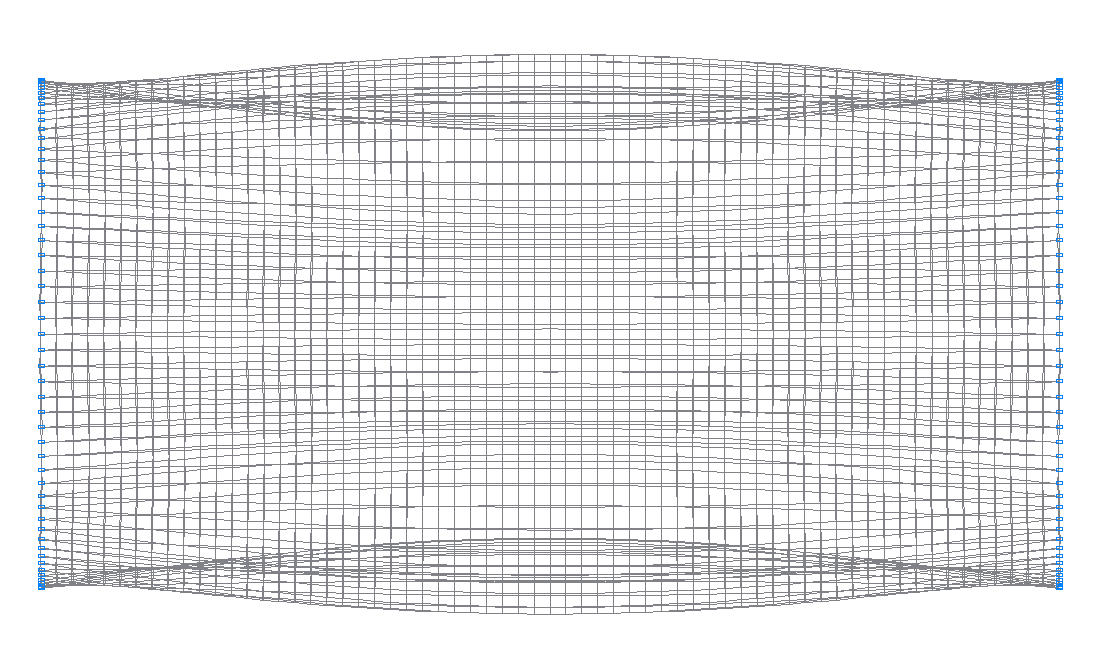
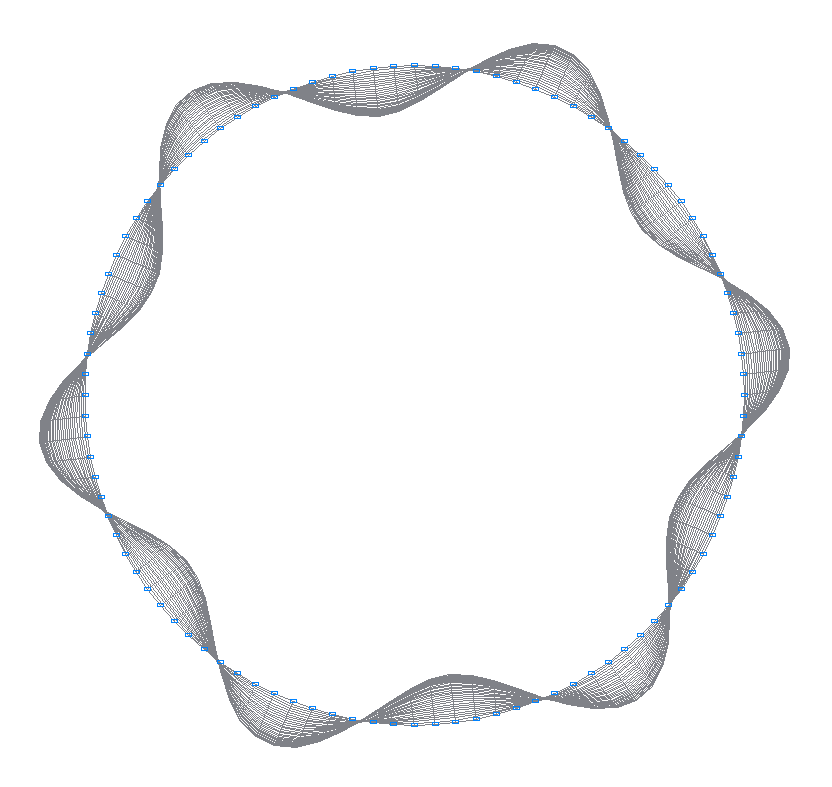
4-th (3-rd theoretical) natural oscillation mode
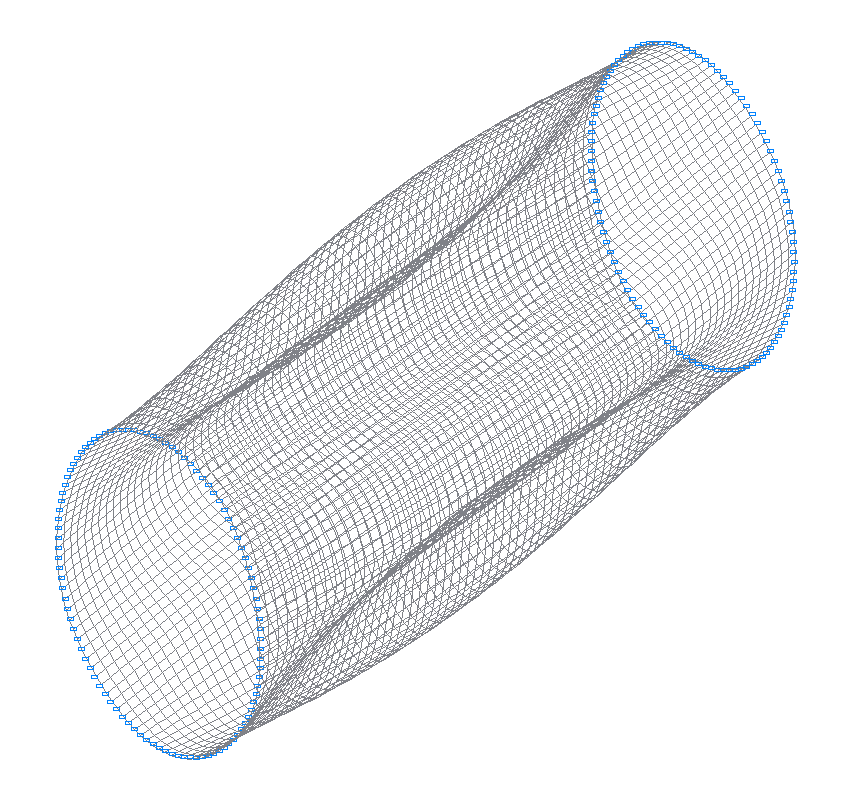

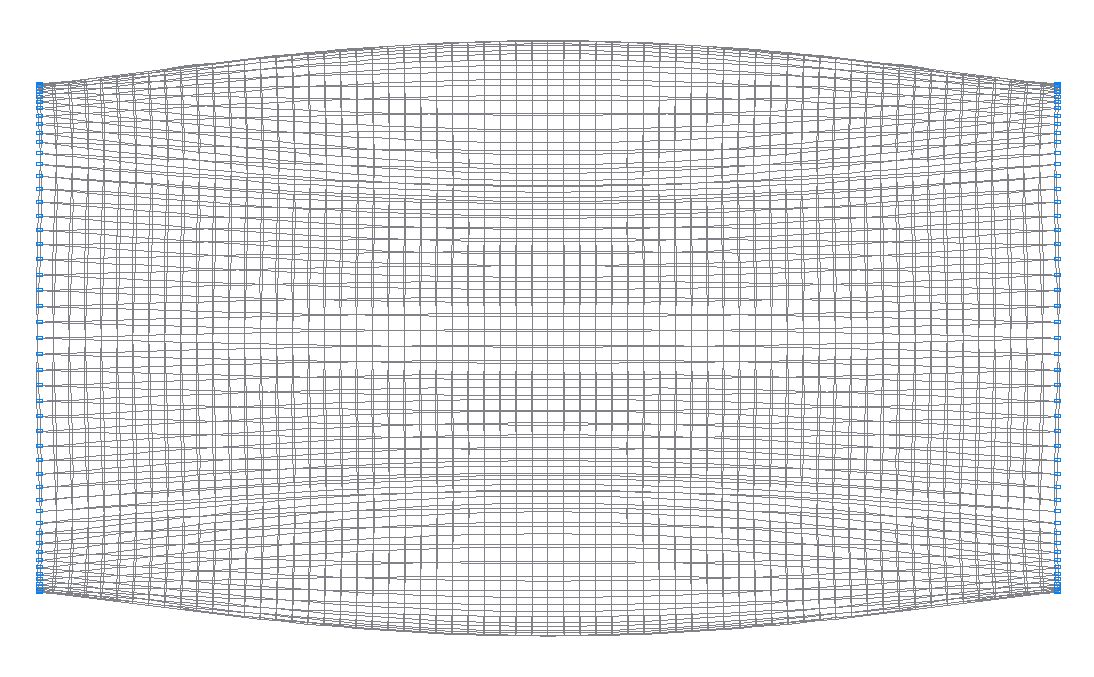

6-th (5-th theoretical) natural oscillation mode
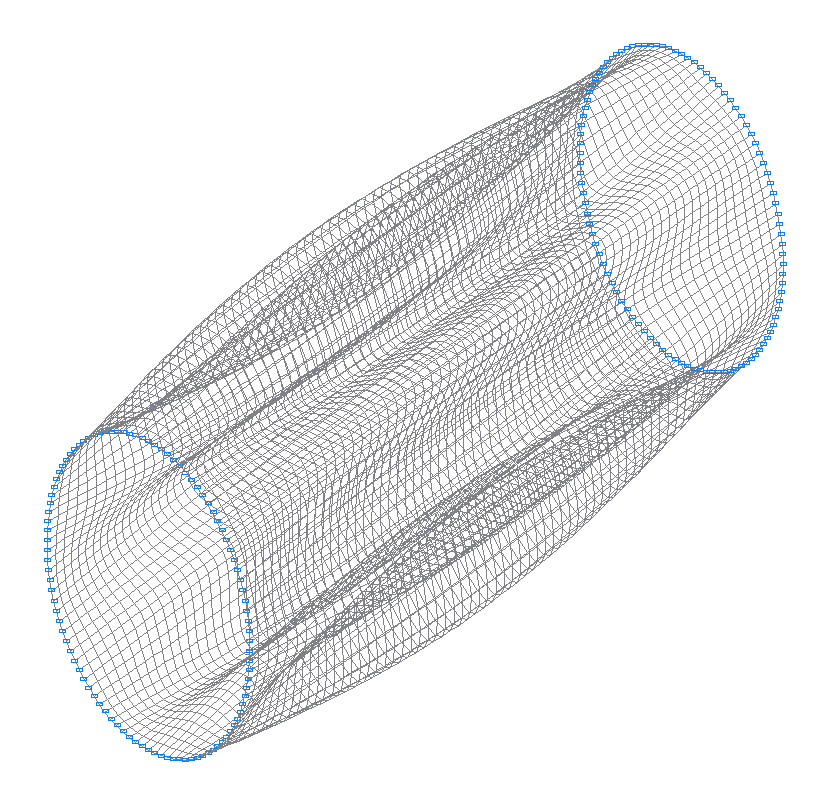

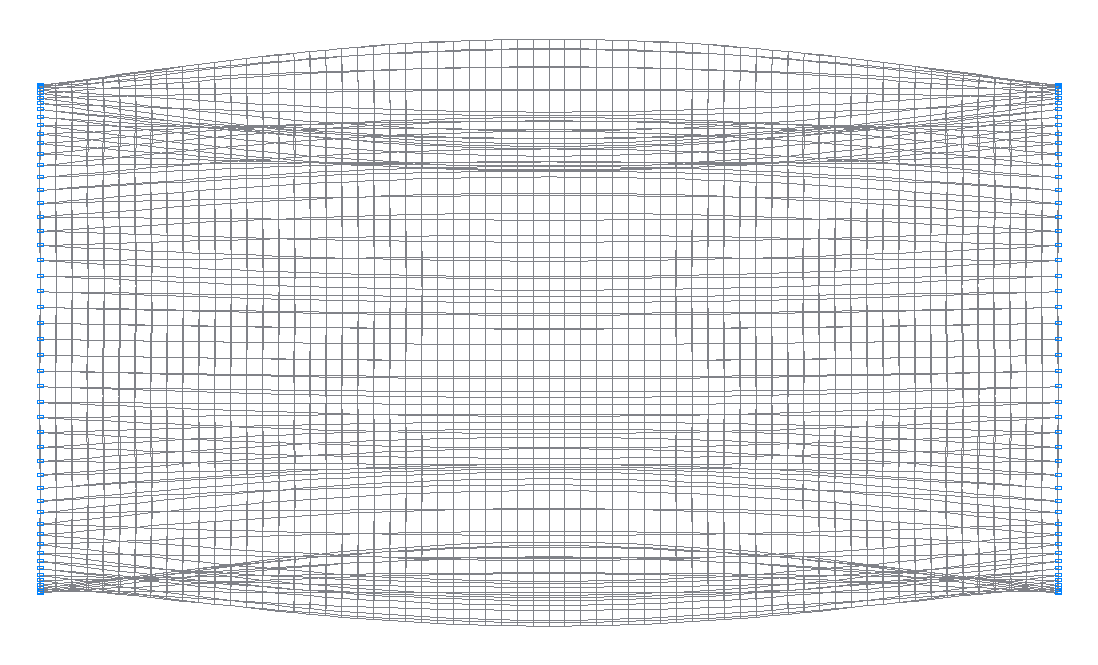
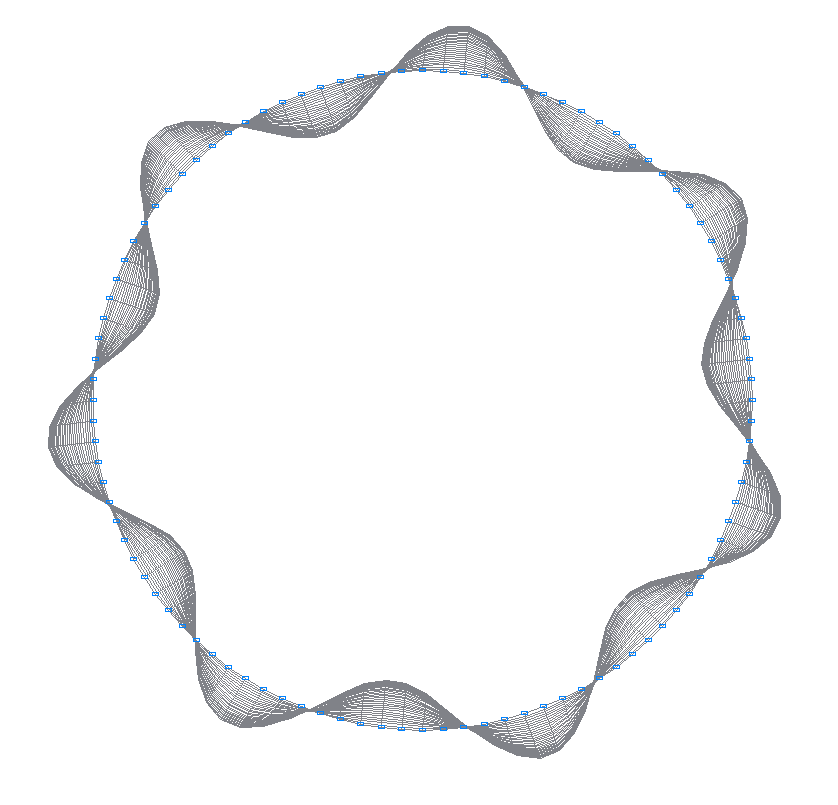
8-th (7-th theoretical) natural oscillation mode

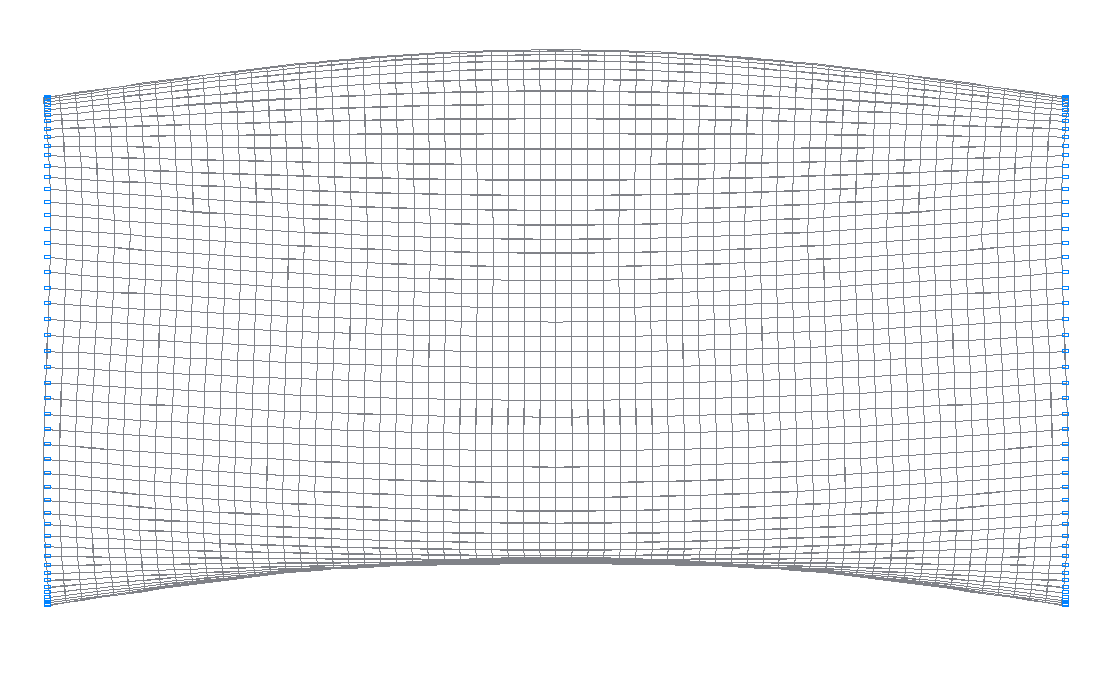
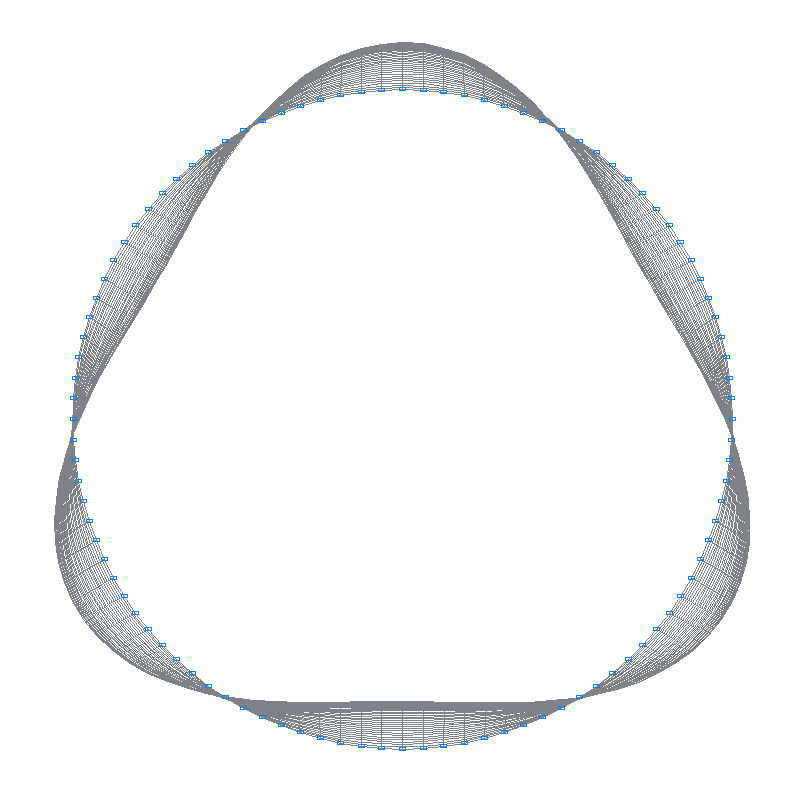
10-th (9-th theoretical) natural oscillation mode
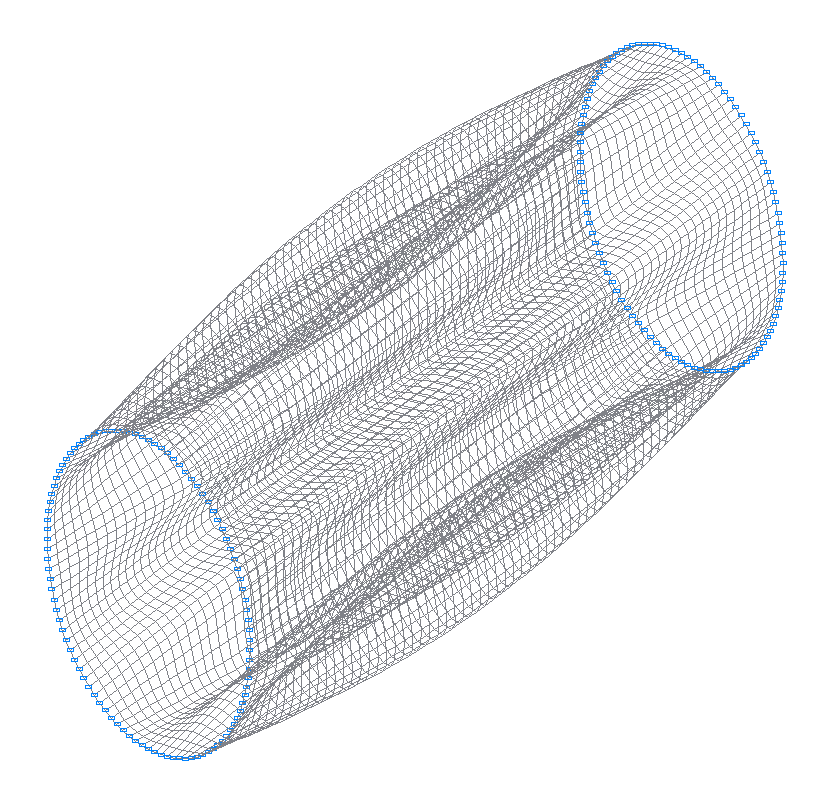

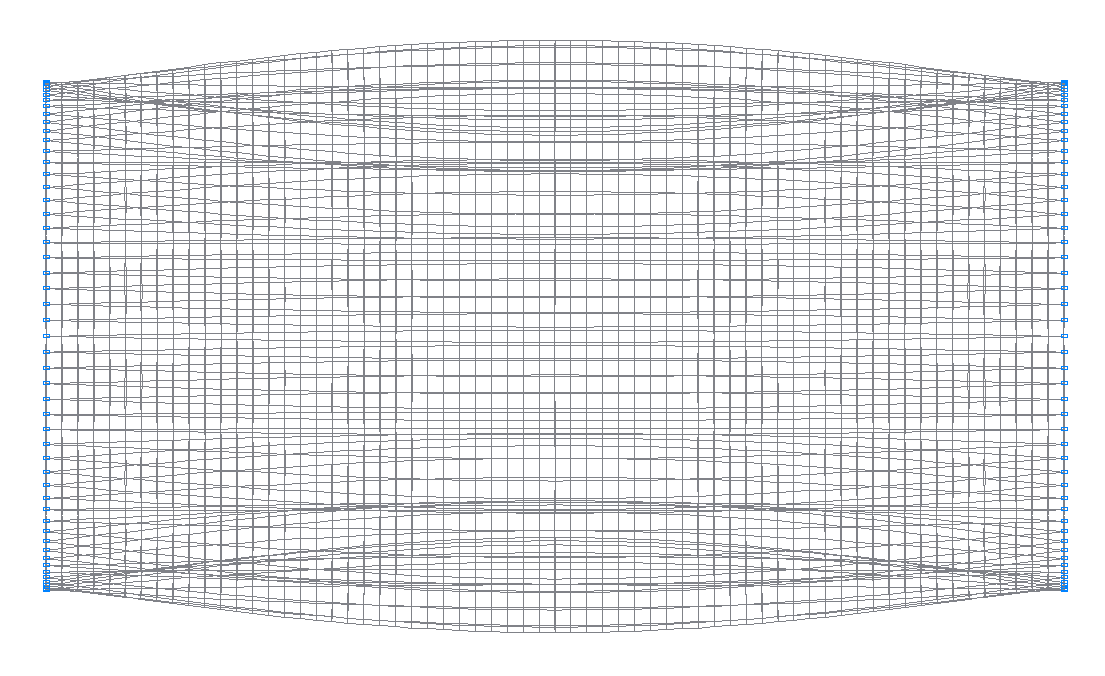
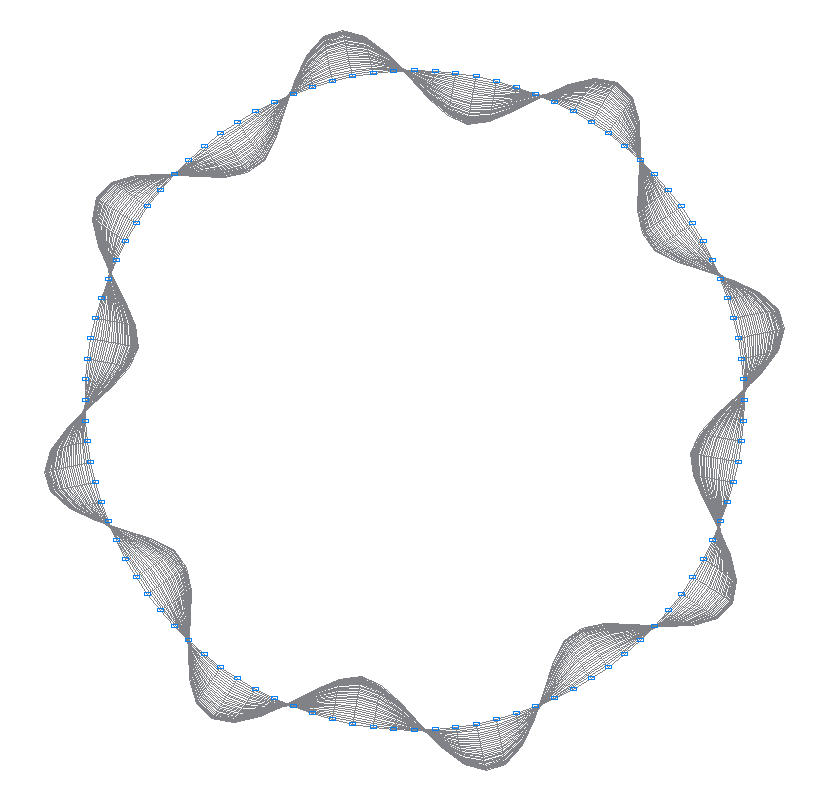
12-th (11-th theoretical) natural oscillation mode
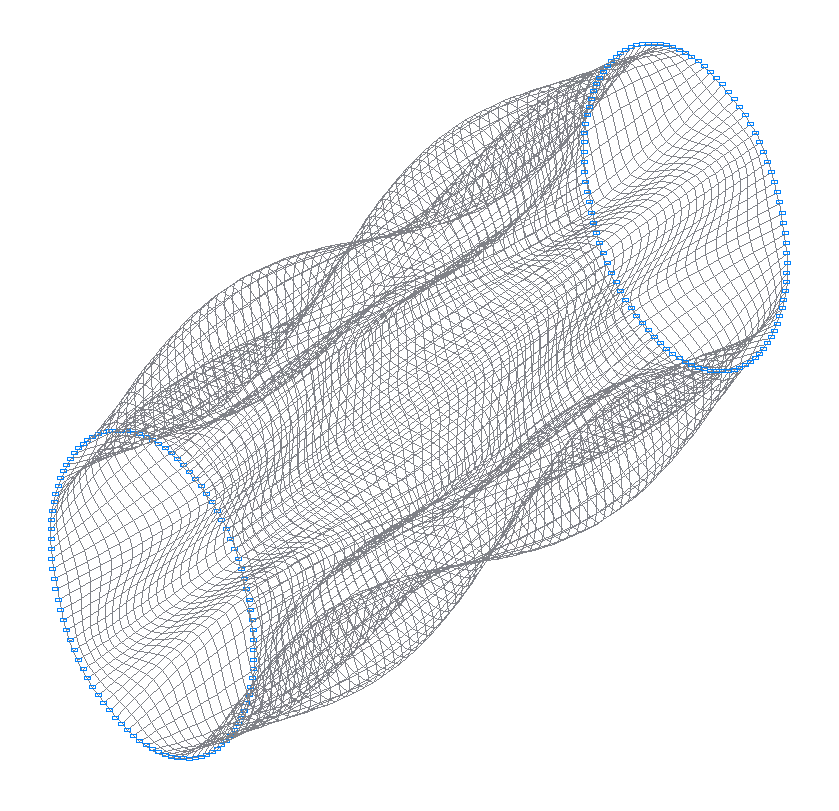


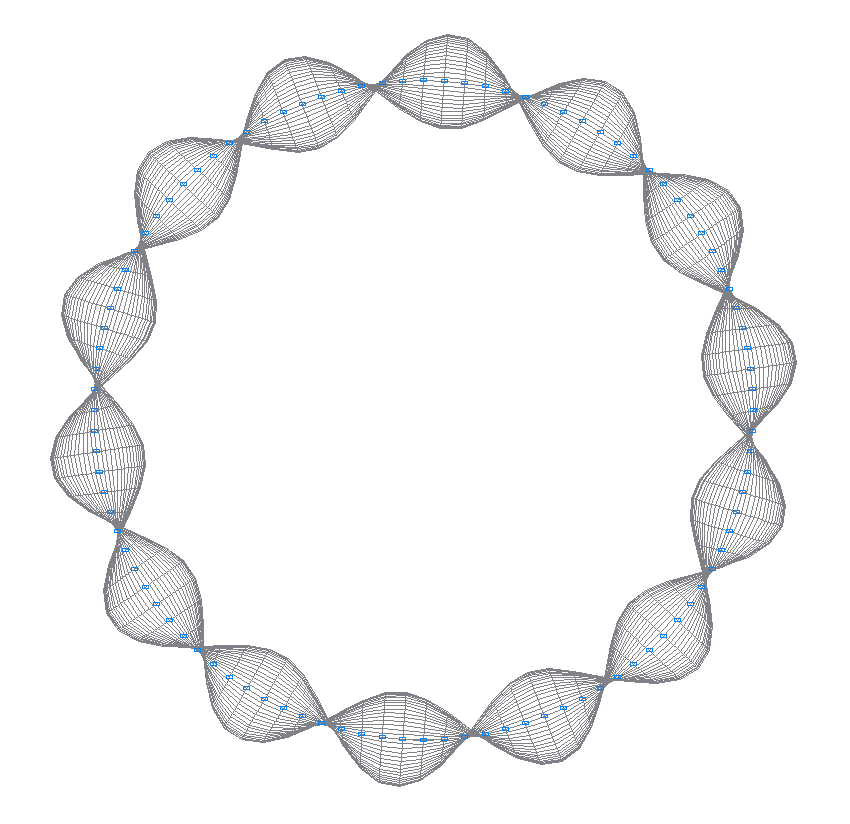
14-th (13-th theoretical) natural oscillation mode
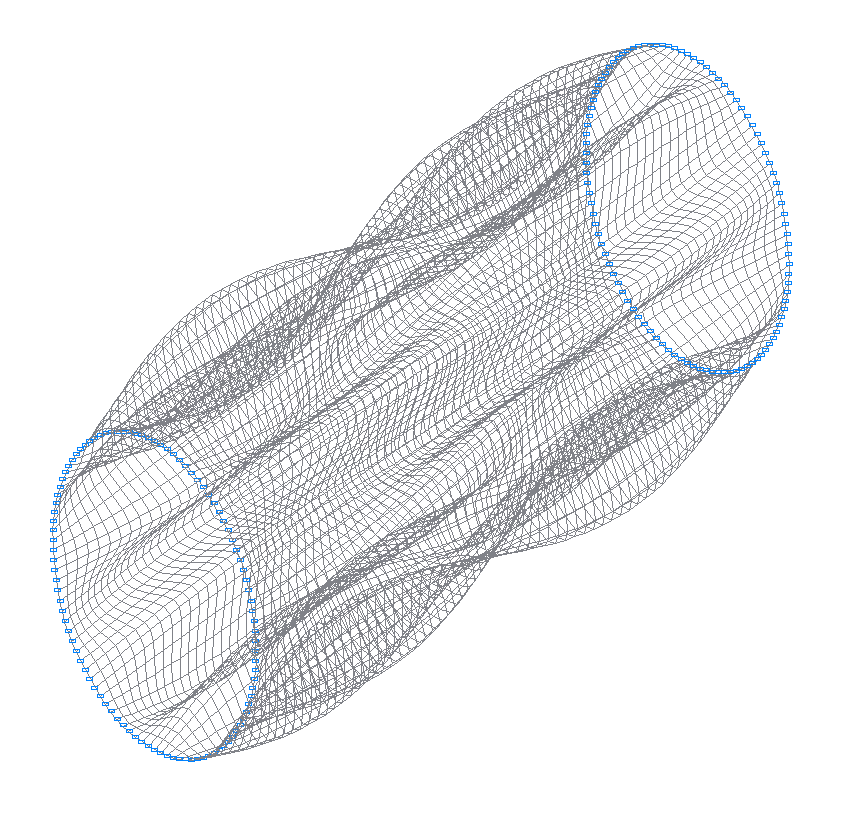
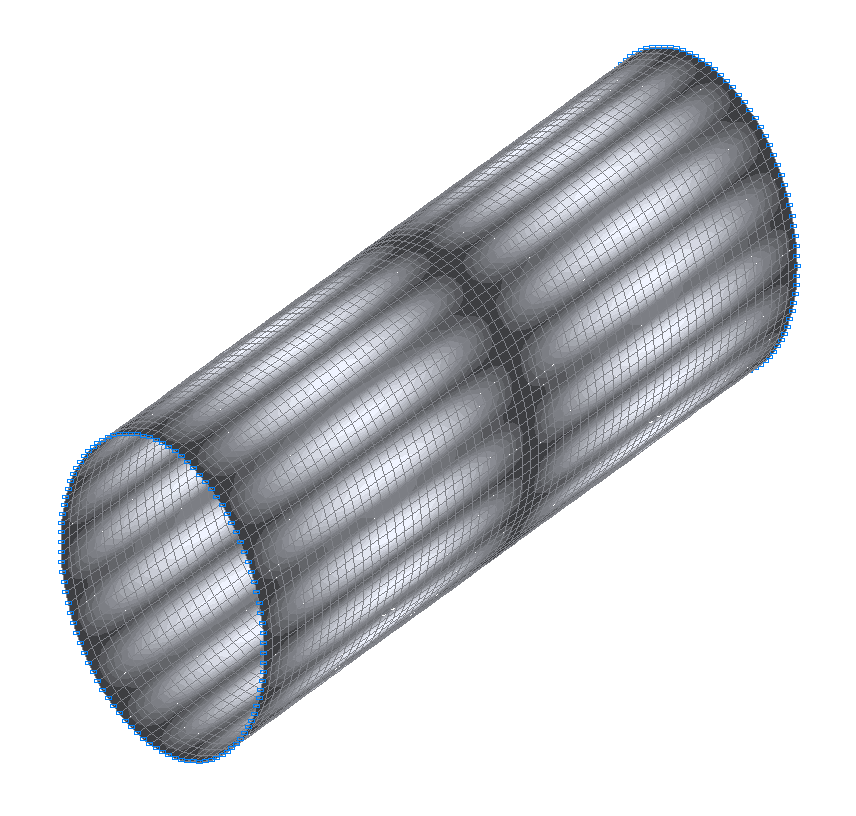


16-th (15-th theoretical) natural oscillation mode



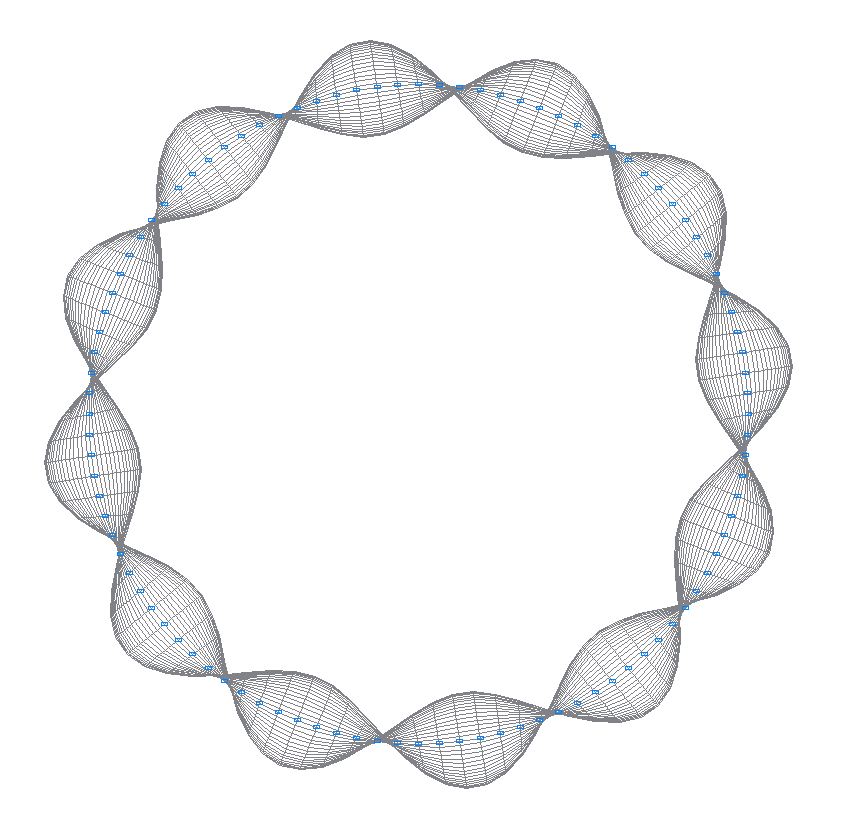
18-th (17-th theoretical) natural oscillation mode
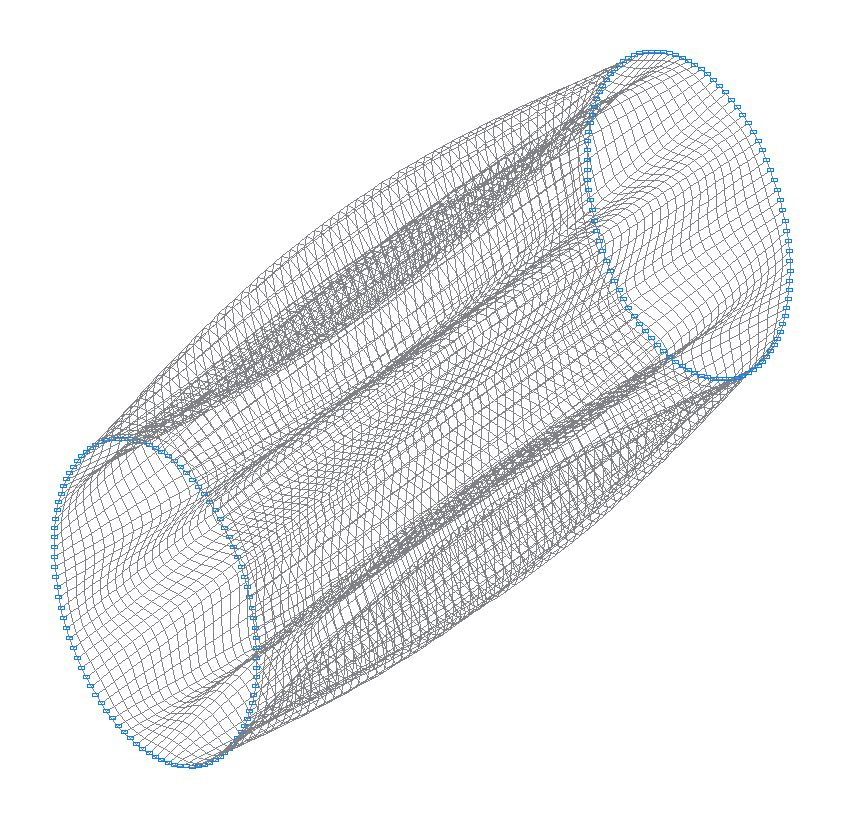

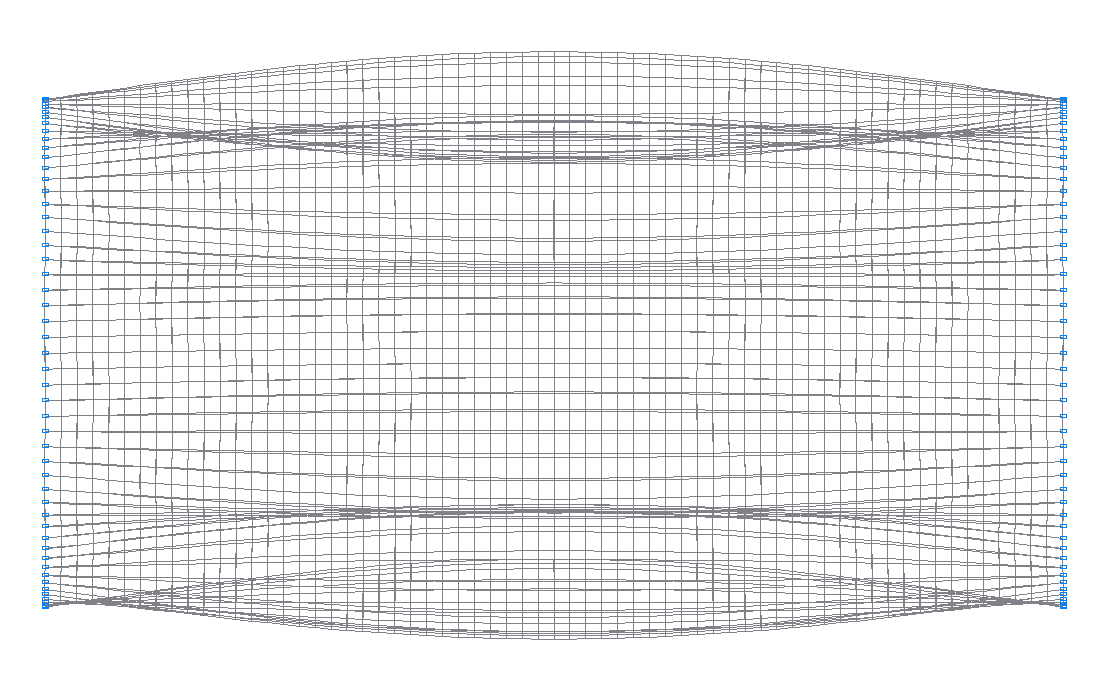
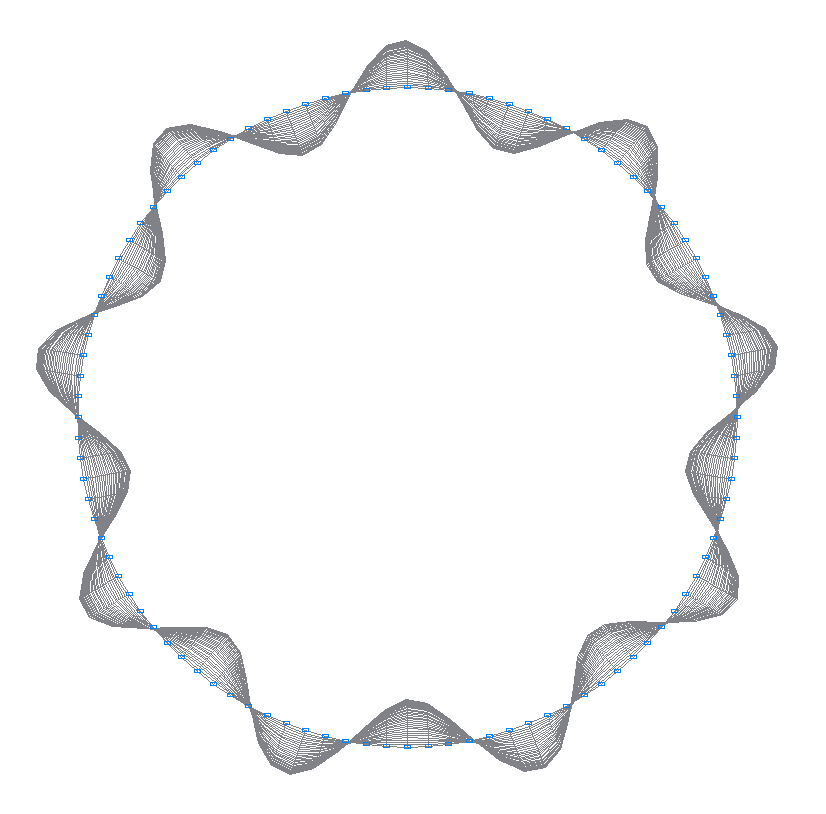
20-th (19-th theoretical) natural oscillation mode



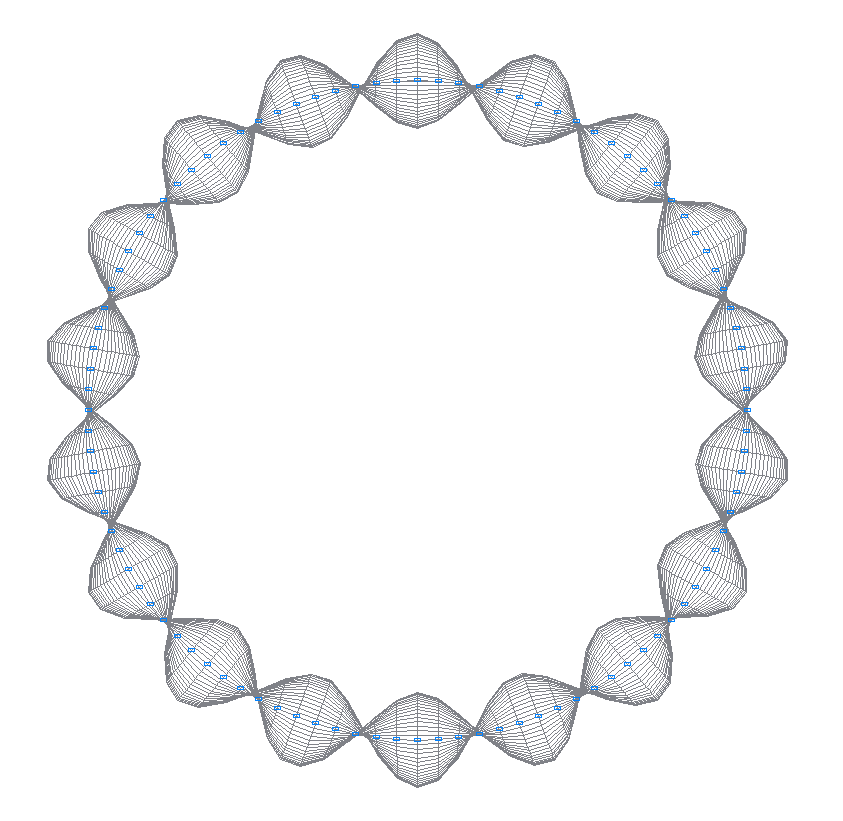
22-nd (21-st theoretical) natural oscillation mode
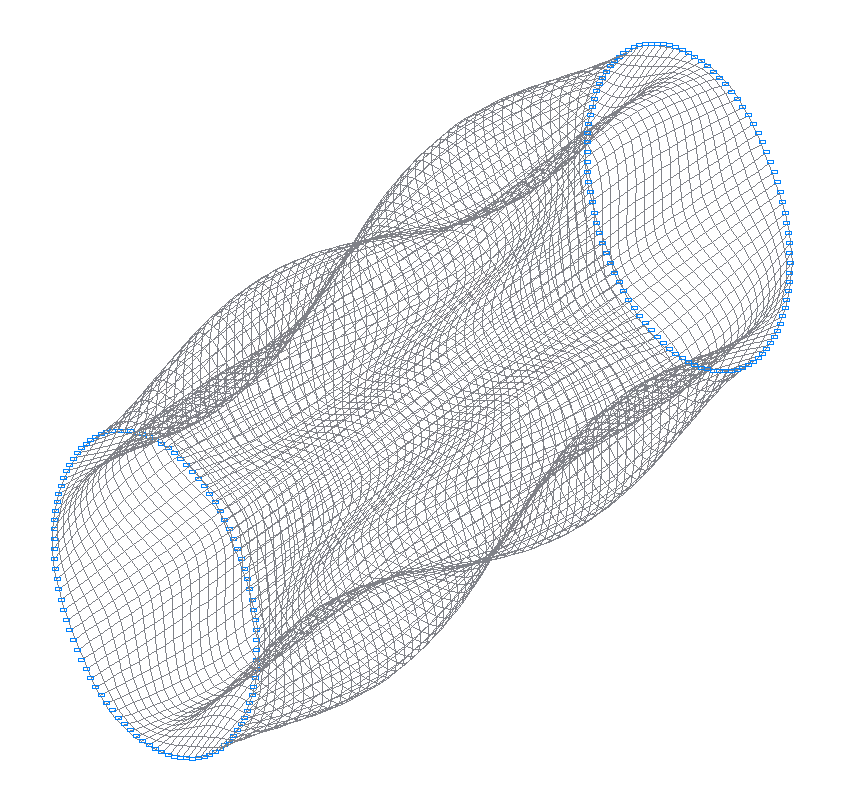
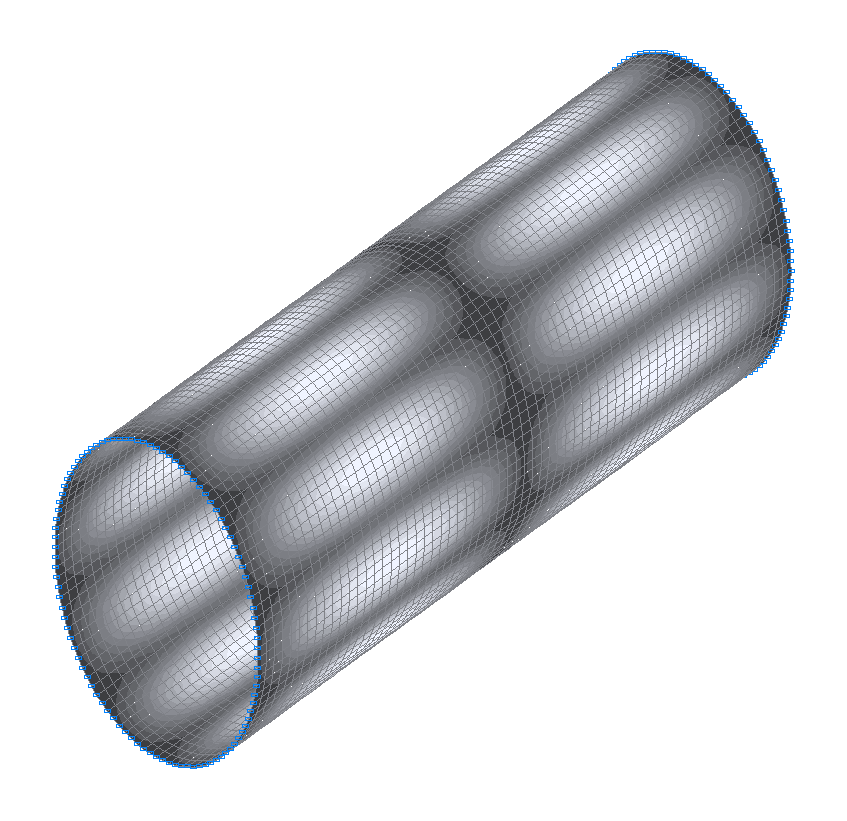
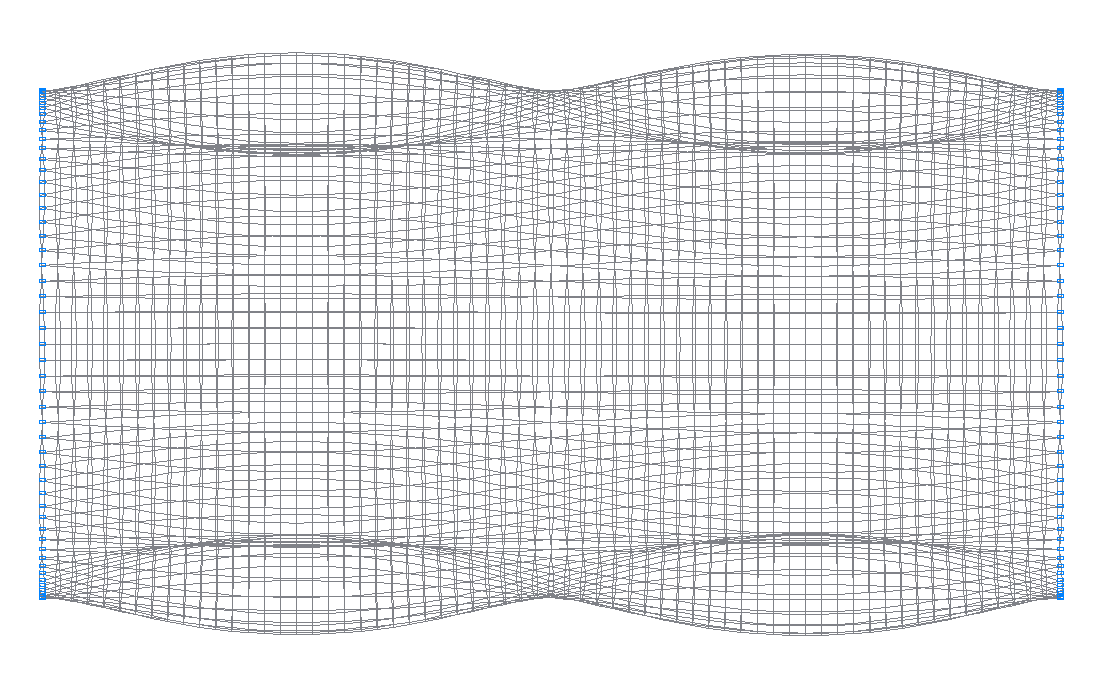
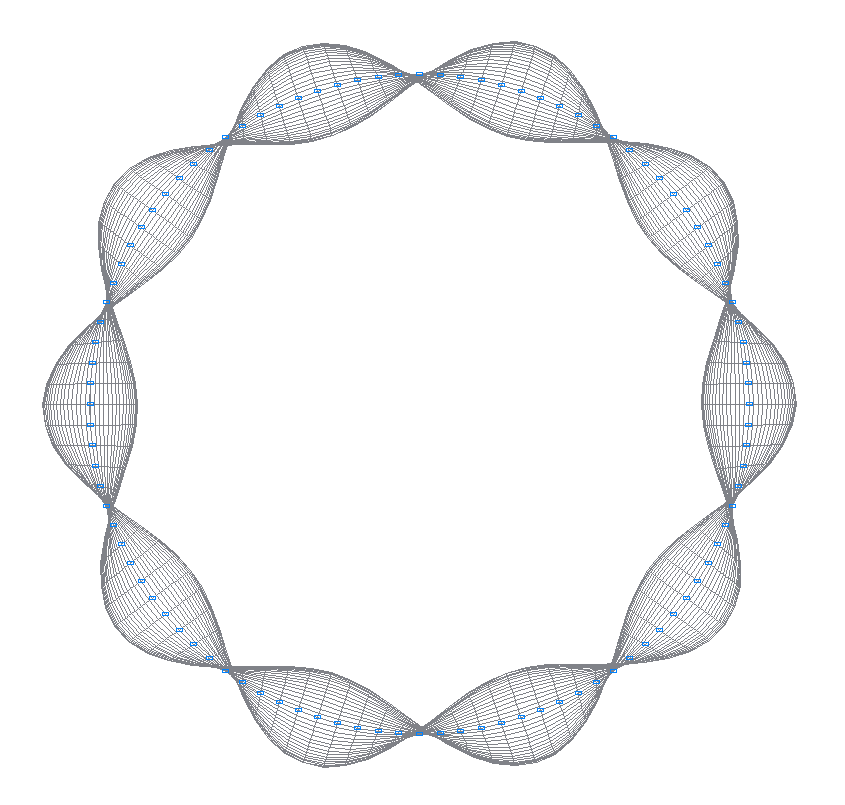
24-th (23-rd theoretical) natural oscillation mode
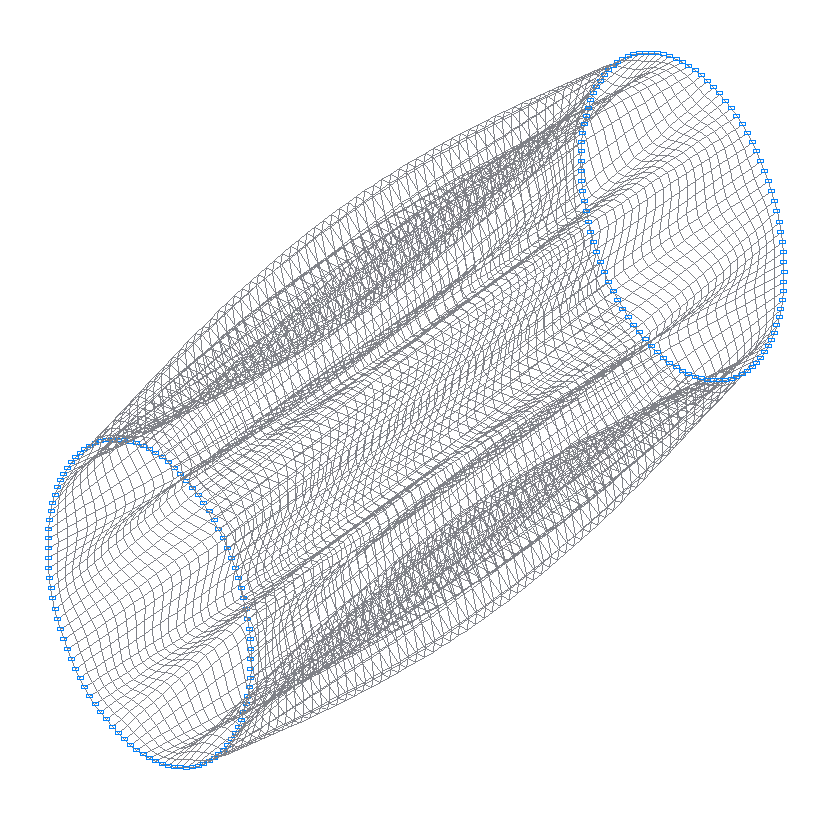

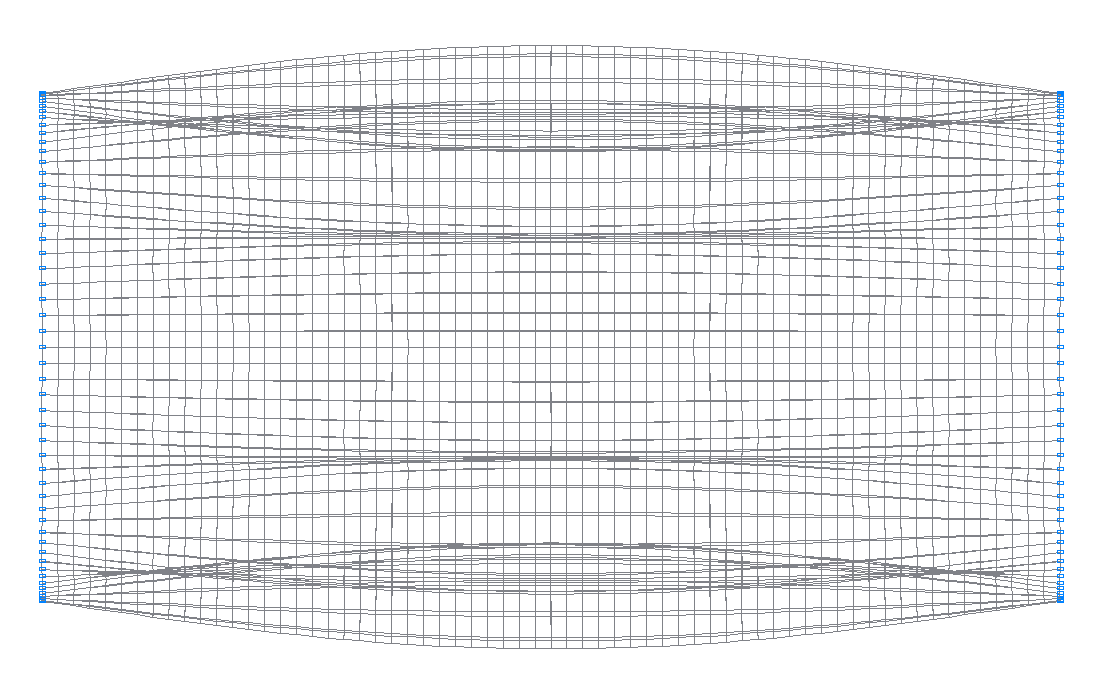
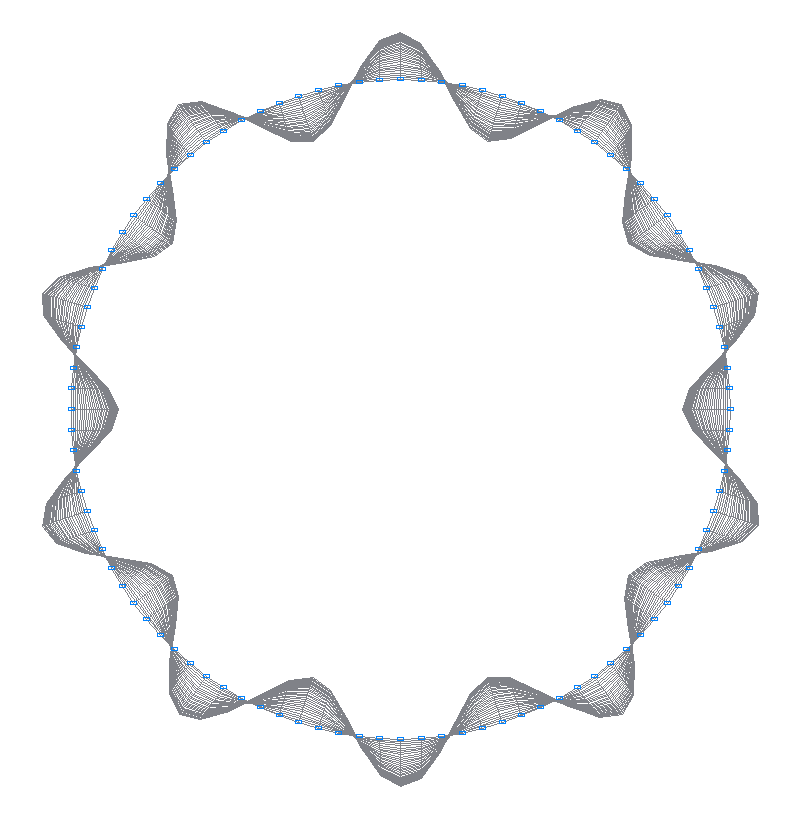
26-th (25-th theoretical) natural oscillation mode
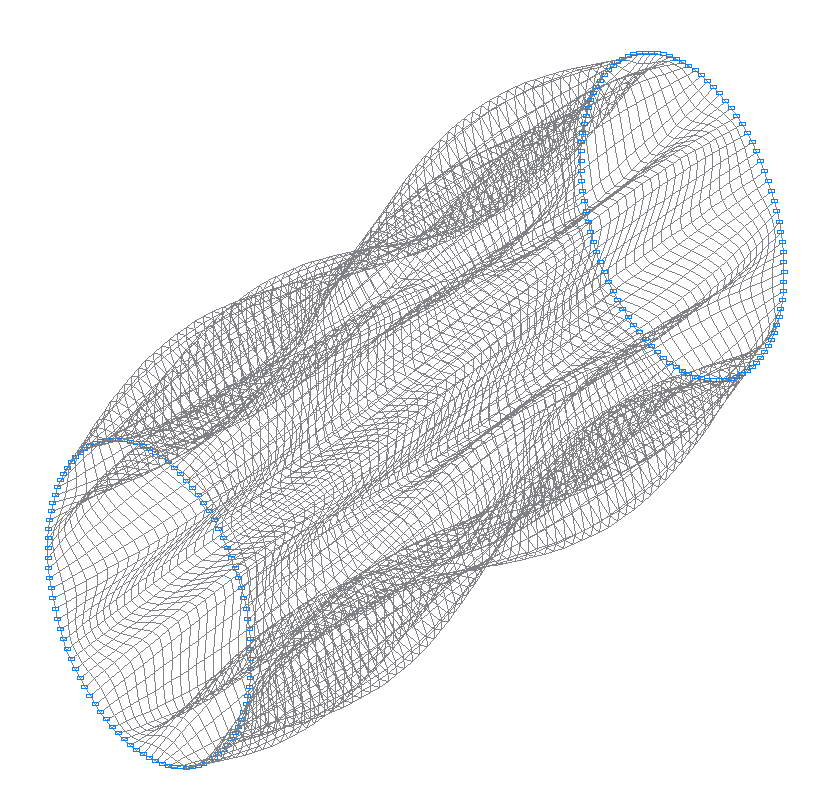
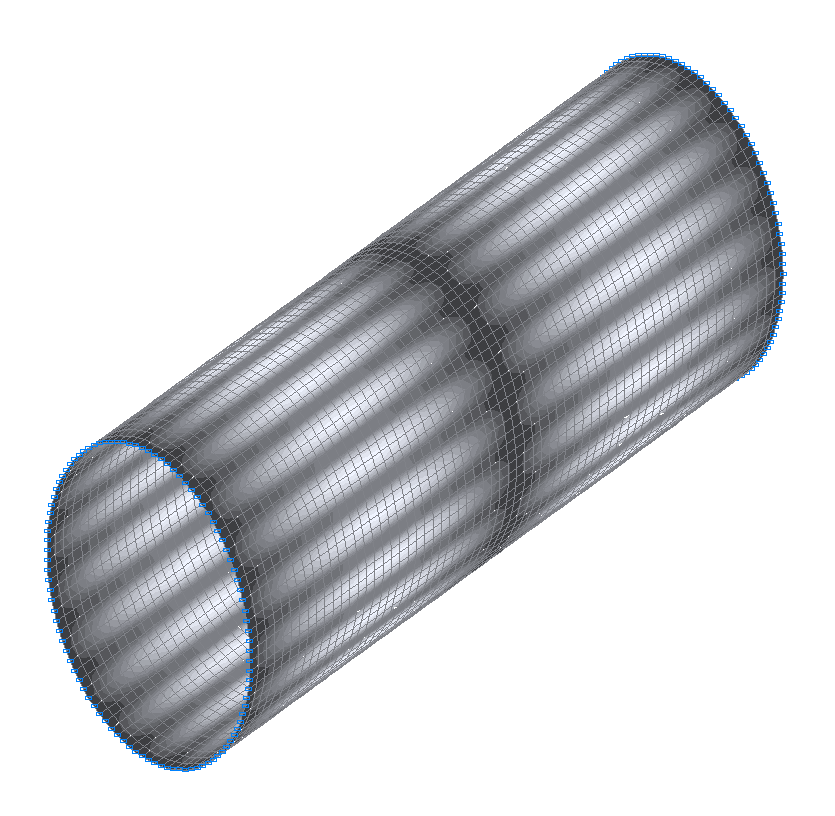
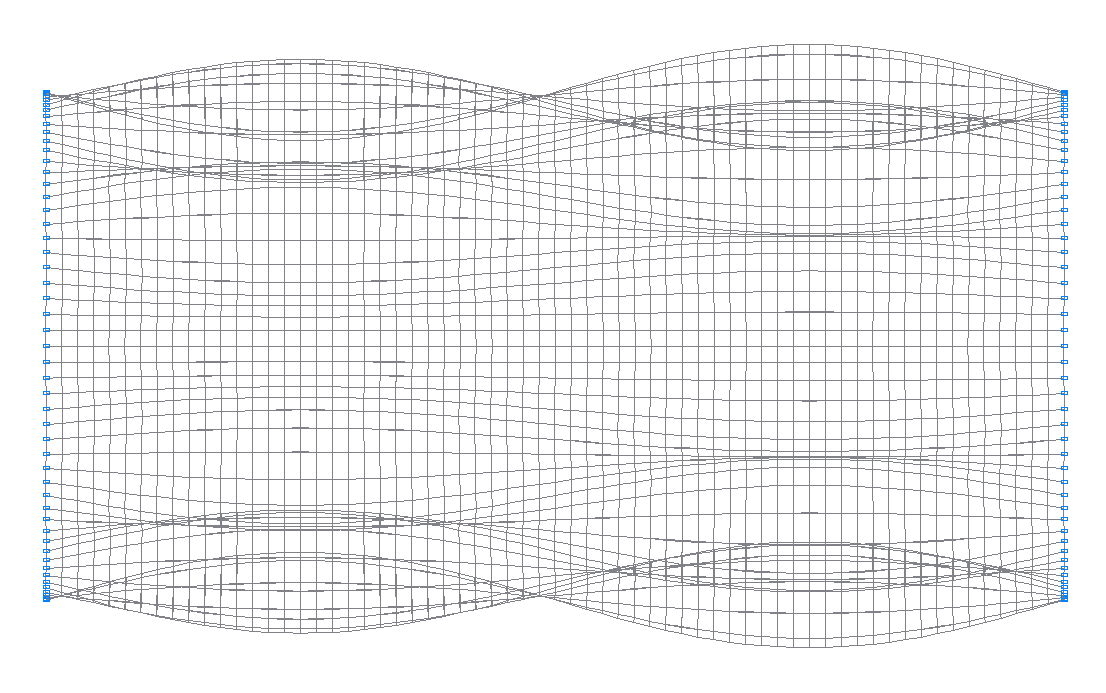
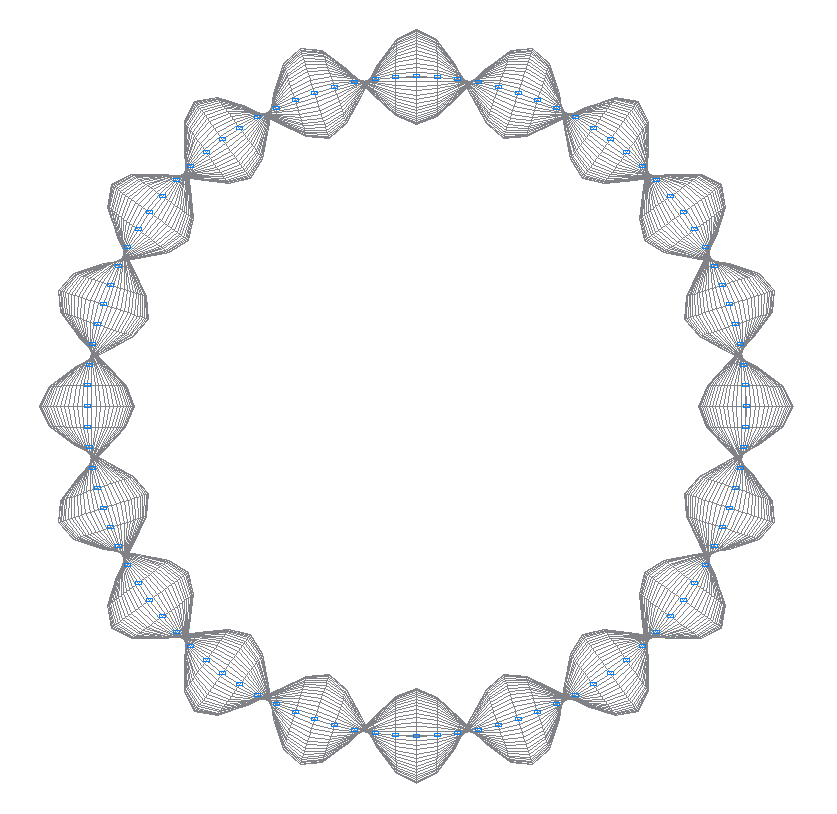
28-th (27-th theoretical) natural oscillation mode
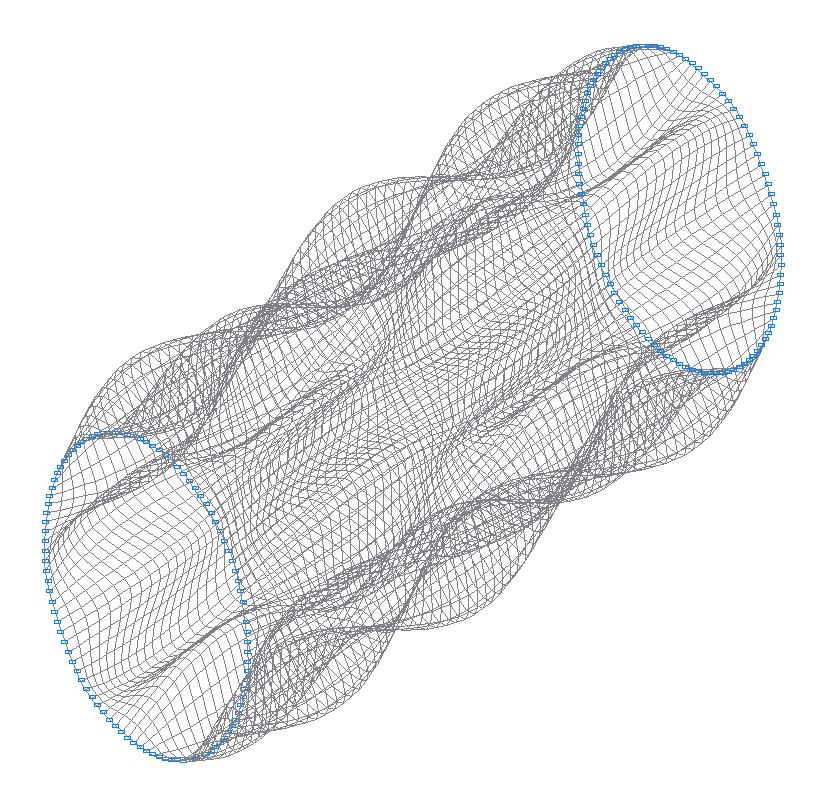
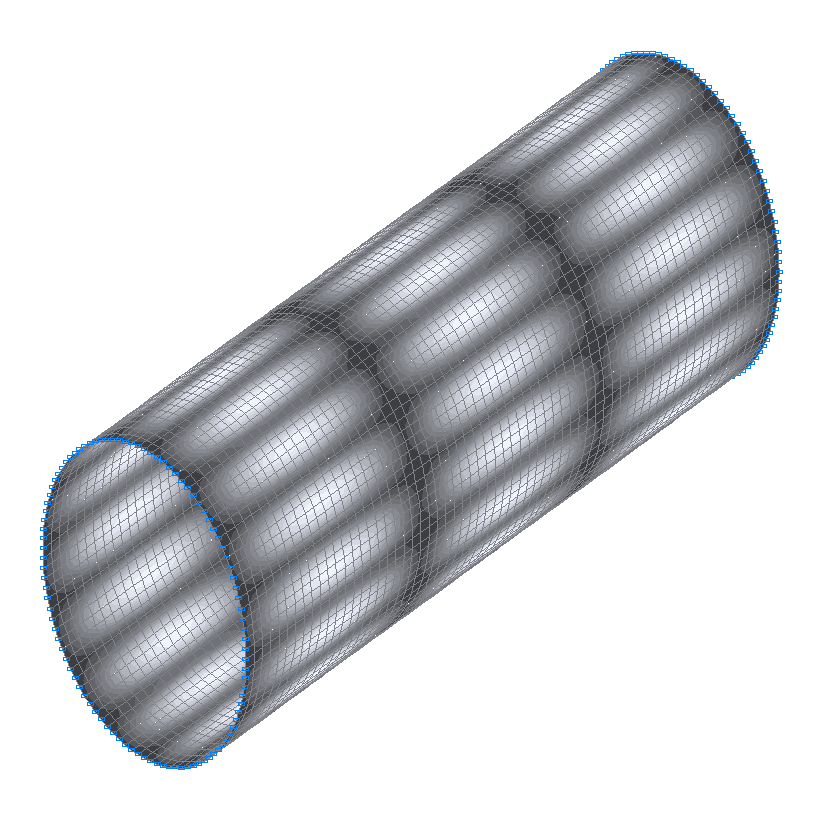
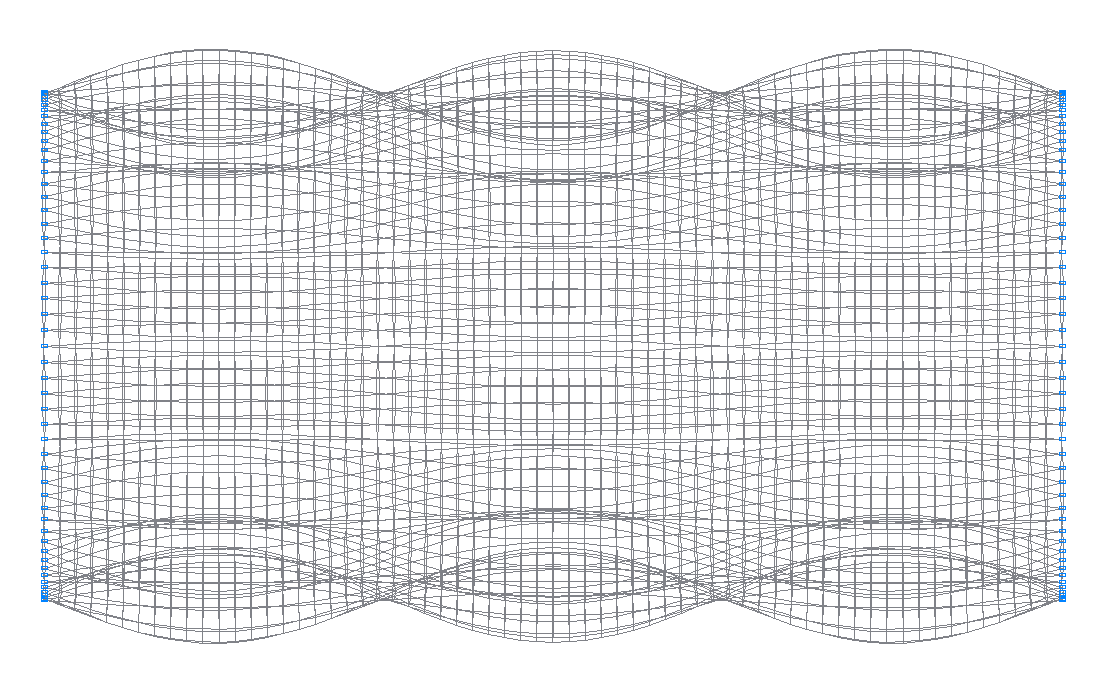
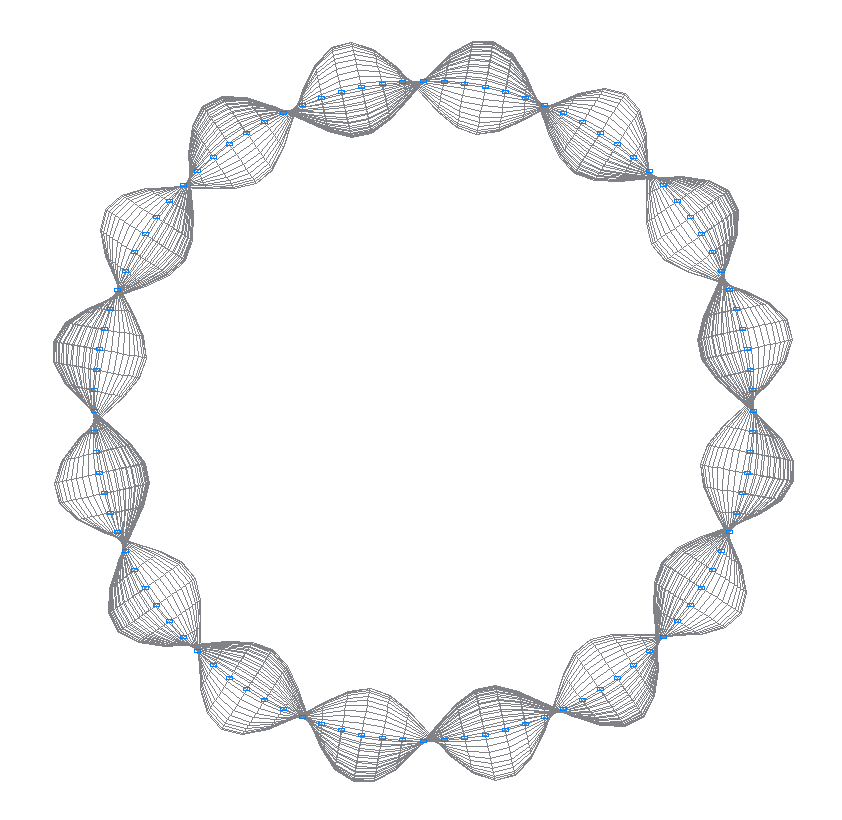
30-th (29-th theoretical) natural oscillation mode
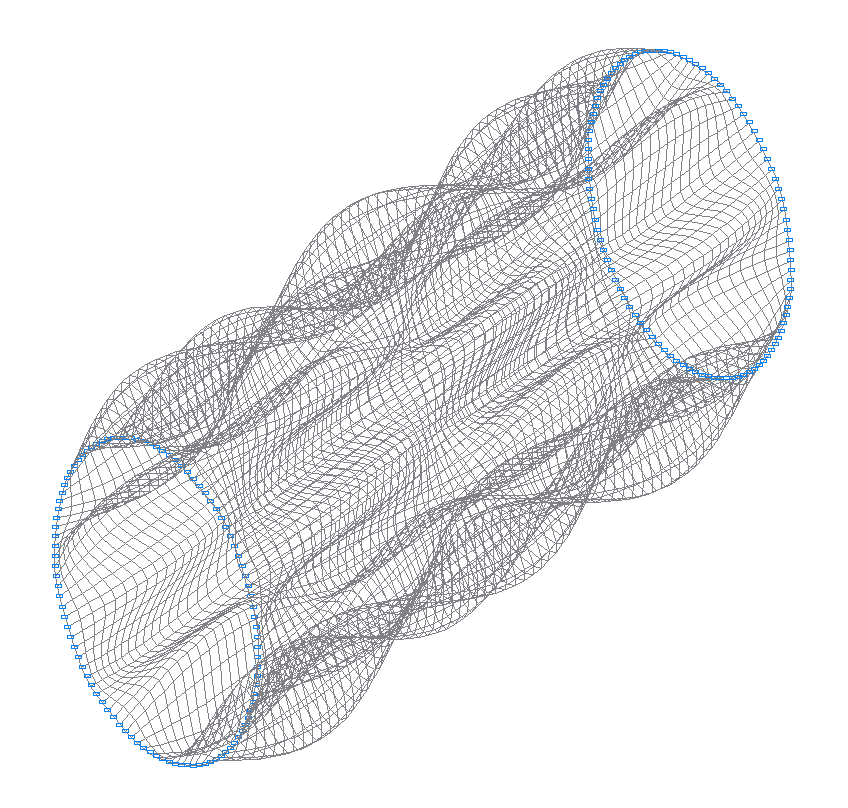
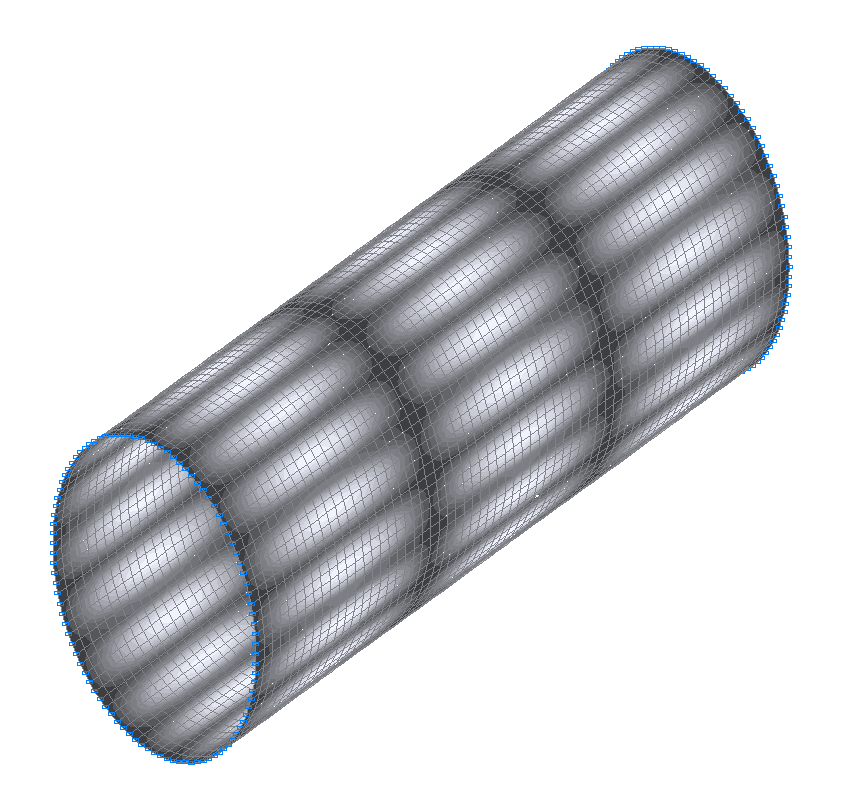
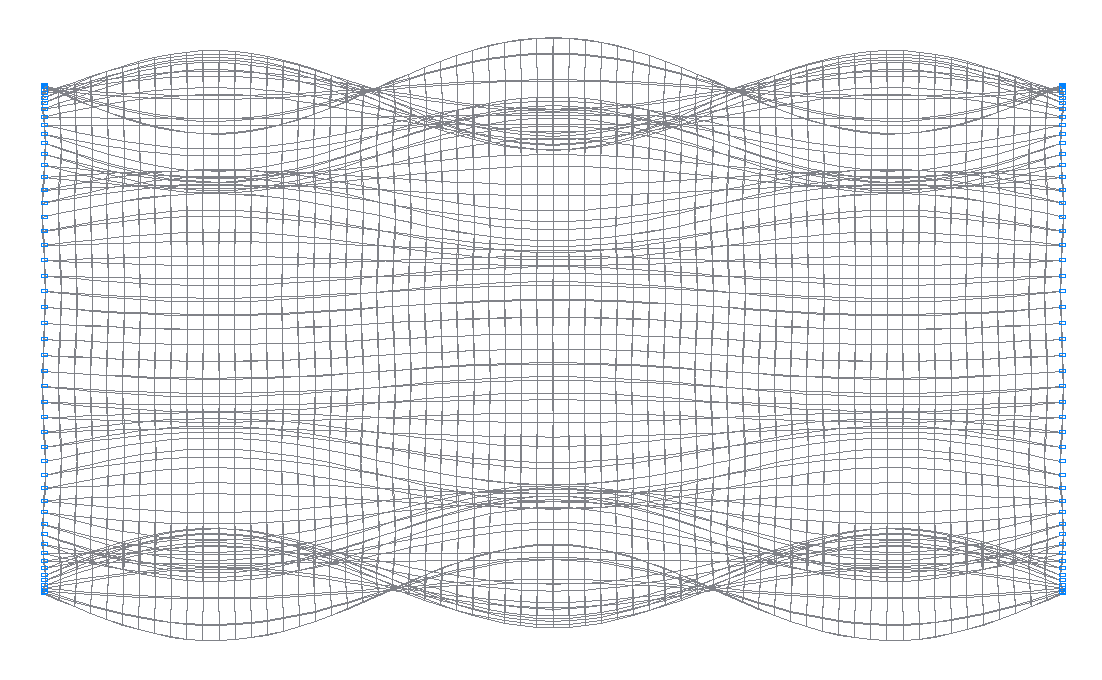
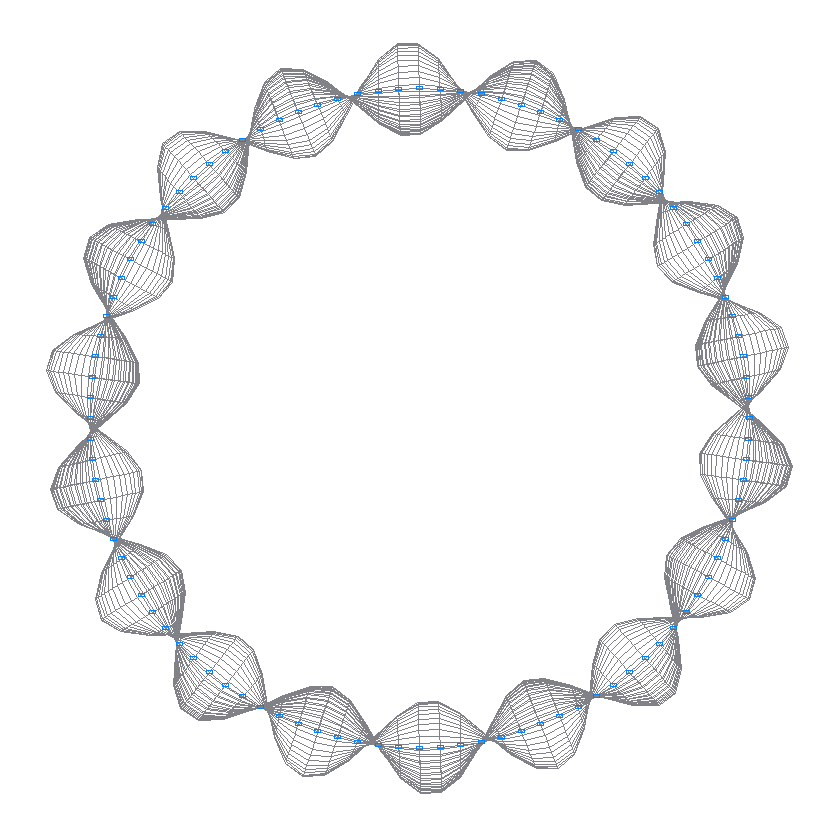
32-nd (31-st theoretical) natural oscillation mode
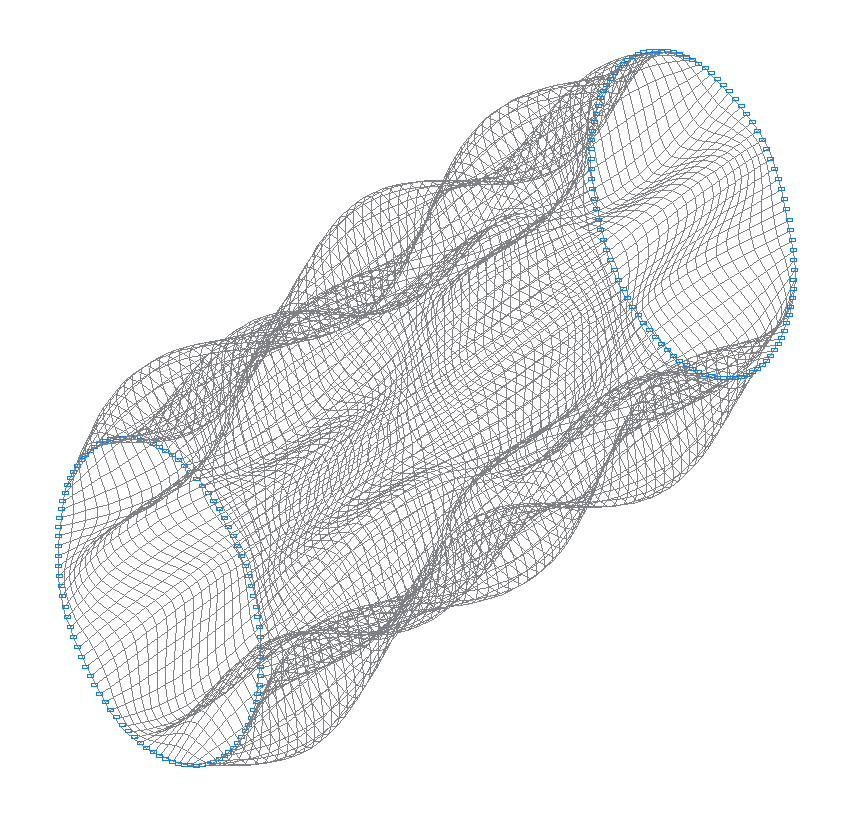
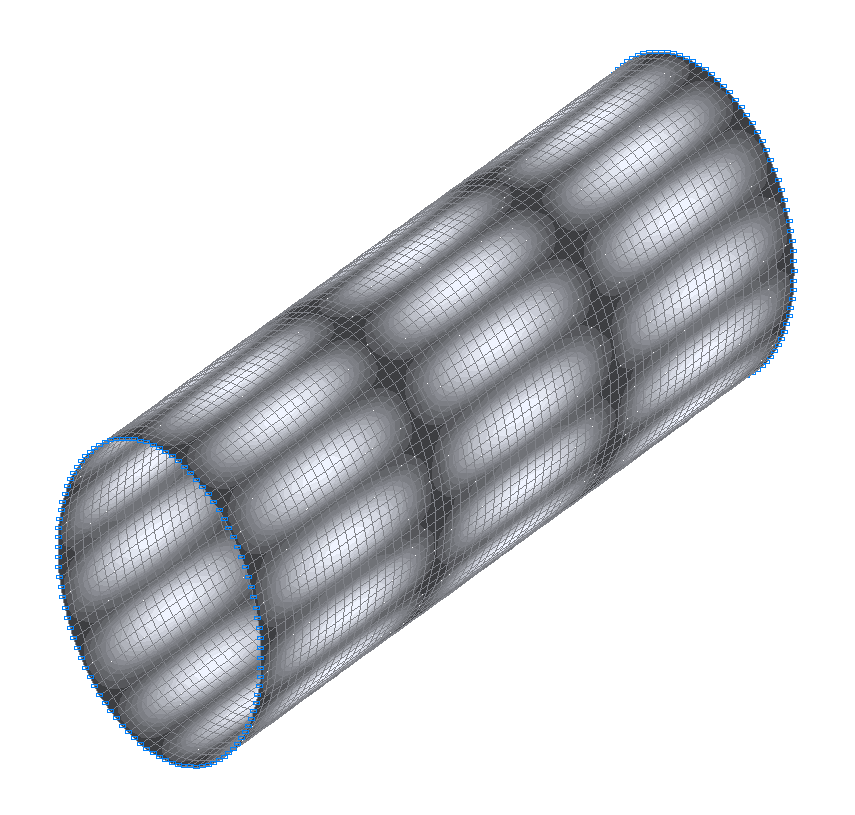
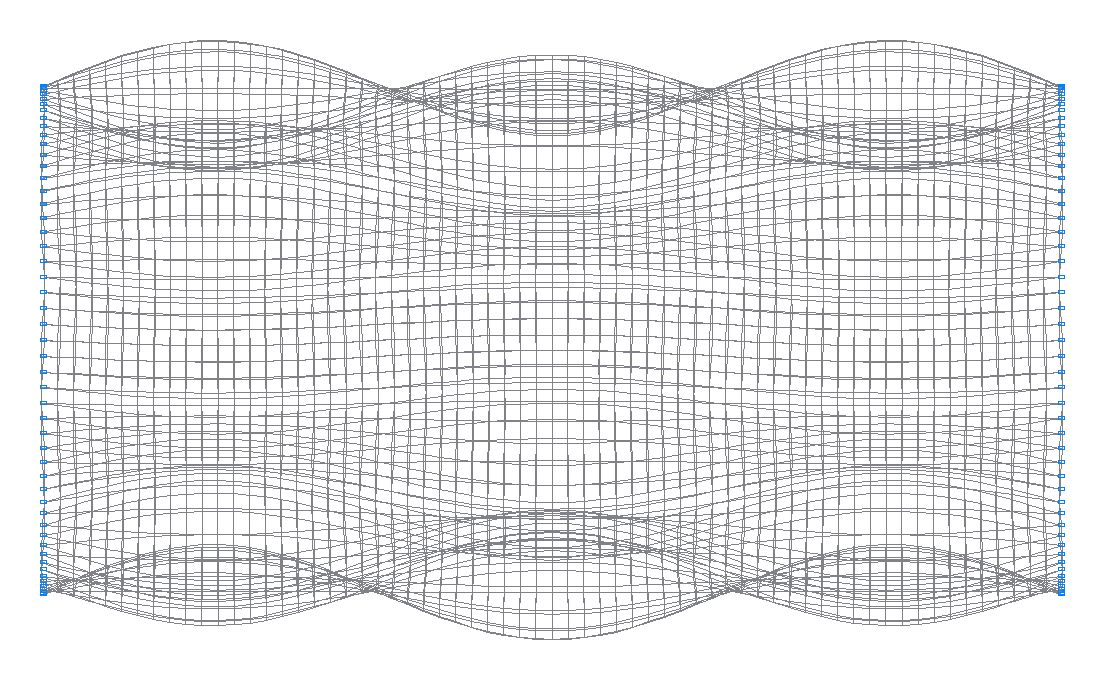
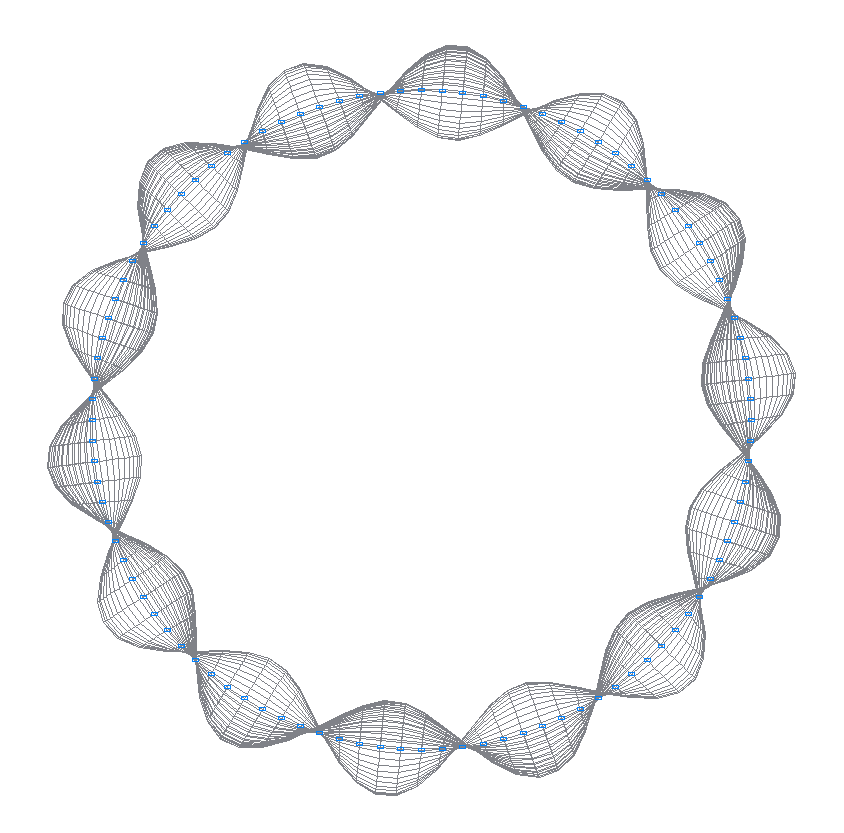
34-th (33-rd theoretical) natural oscillation mode
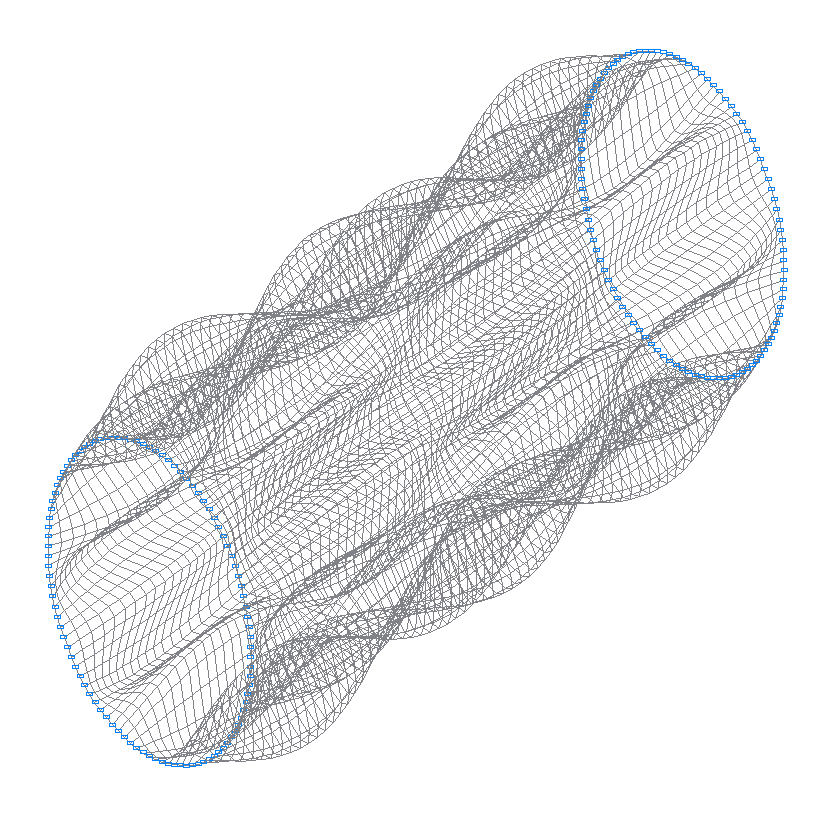
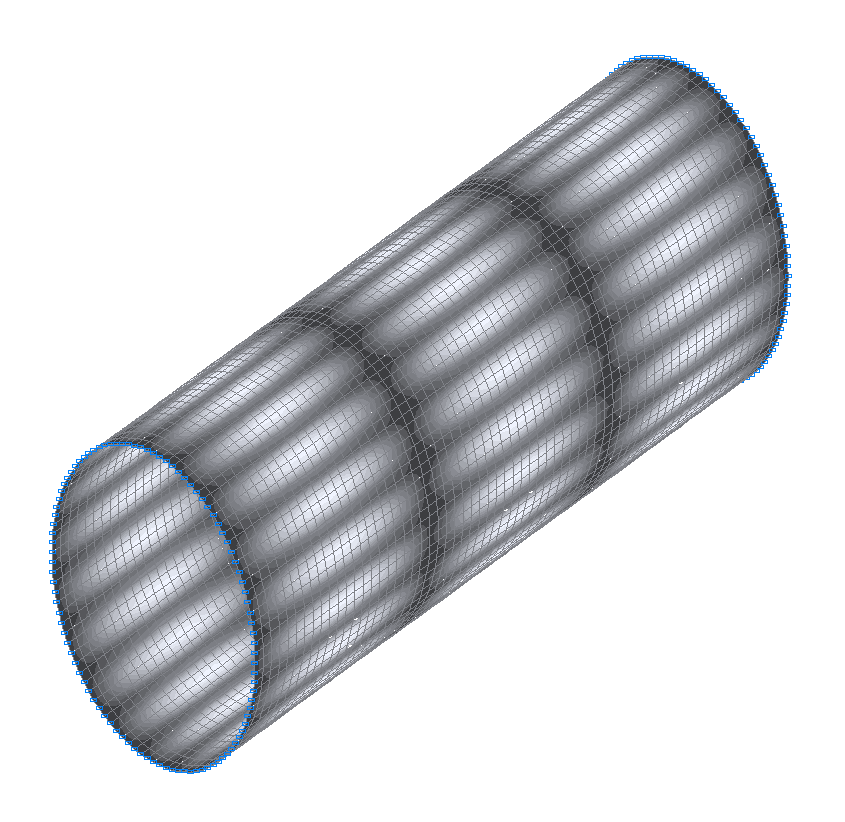
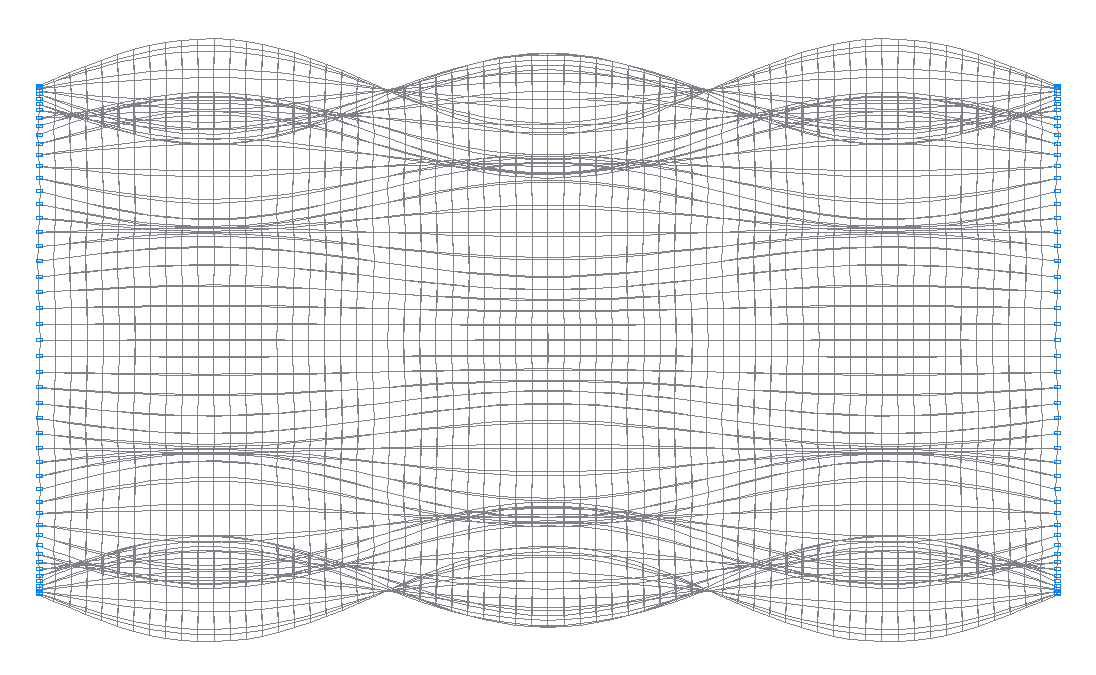
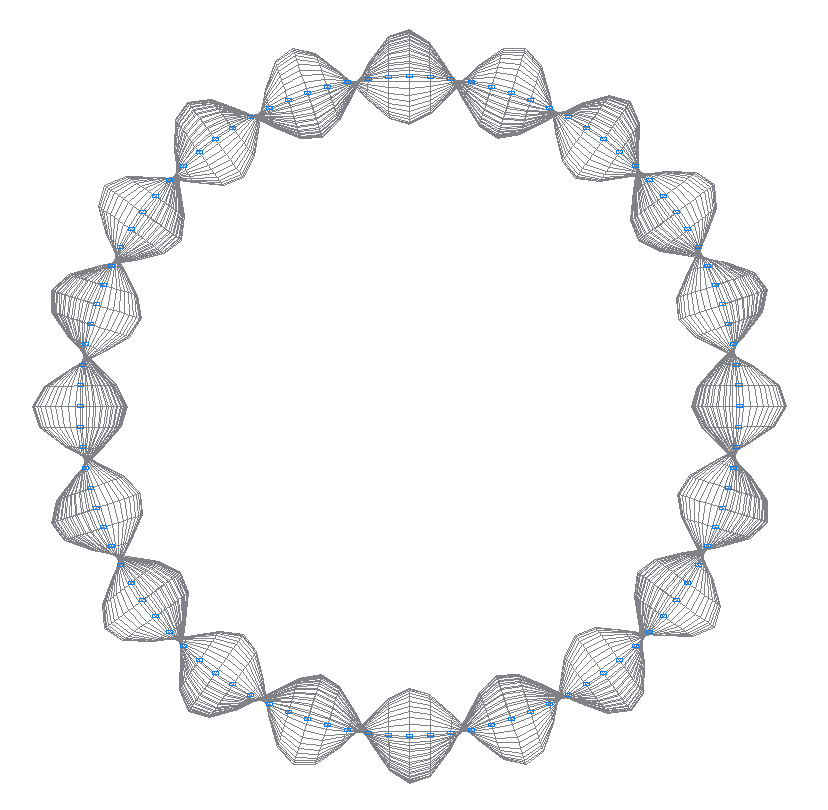
36-th (35-th theoretical) natural oscillation mode
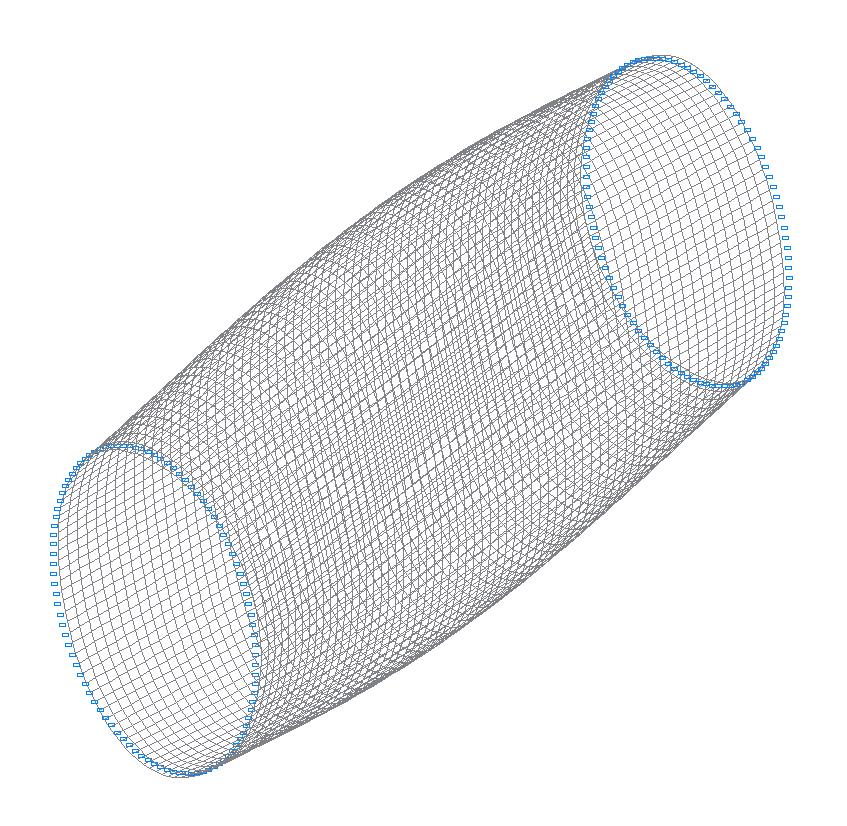


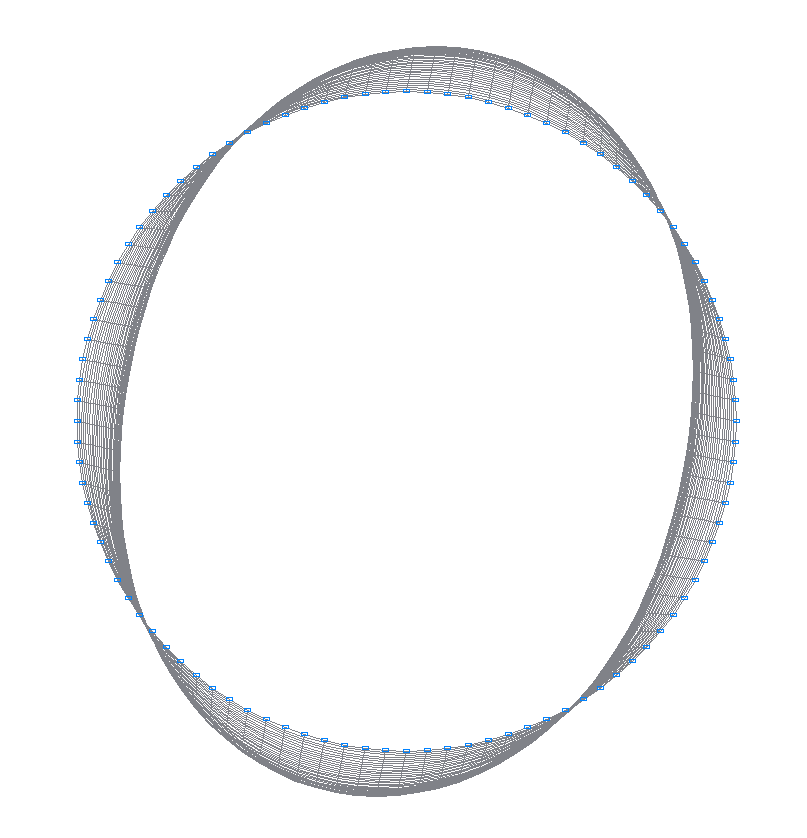
38-th (37-th theoretical) natural oscillation mode
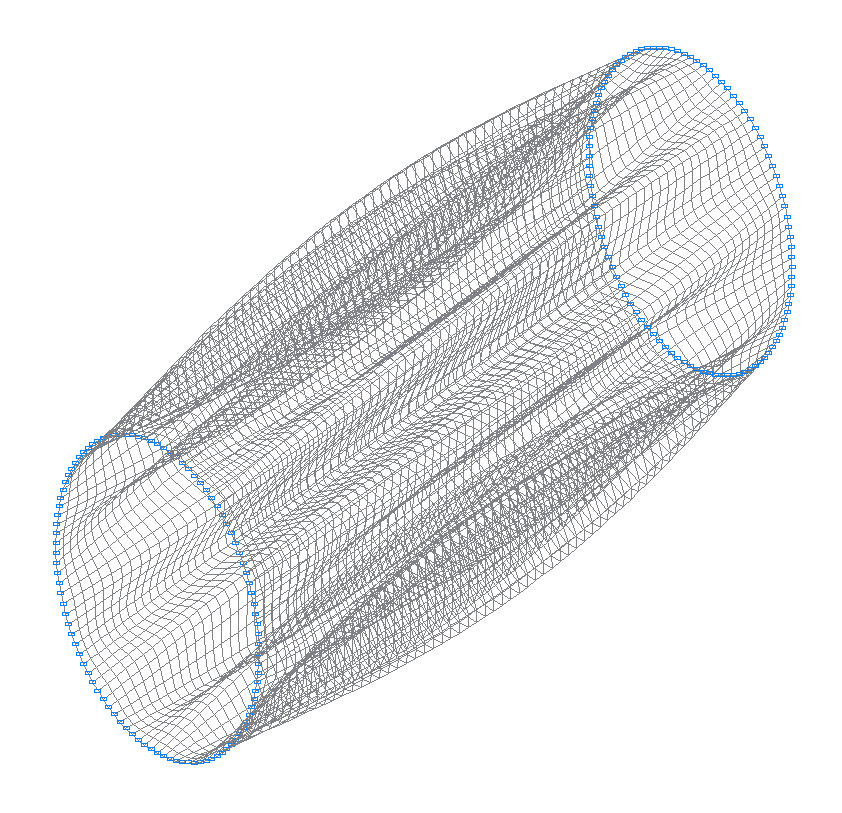

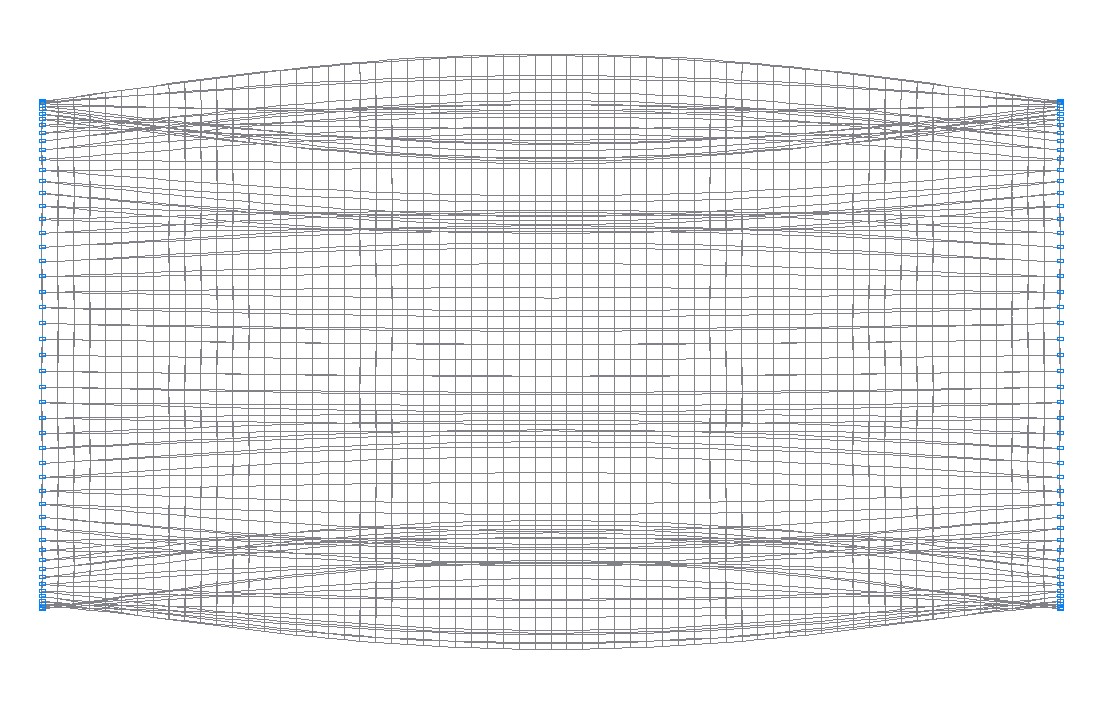
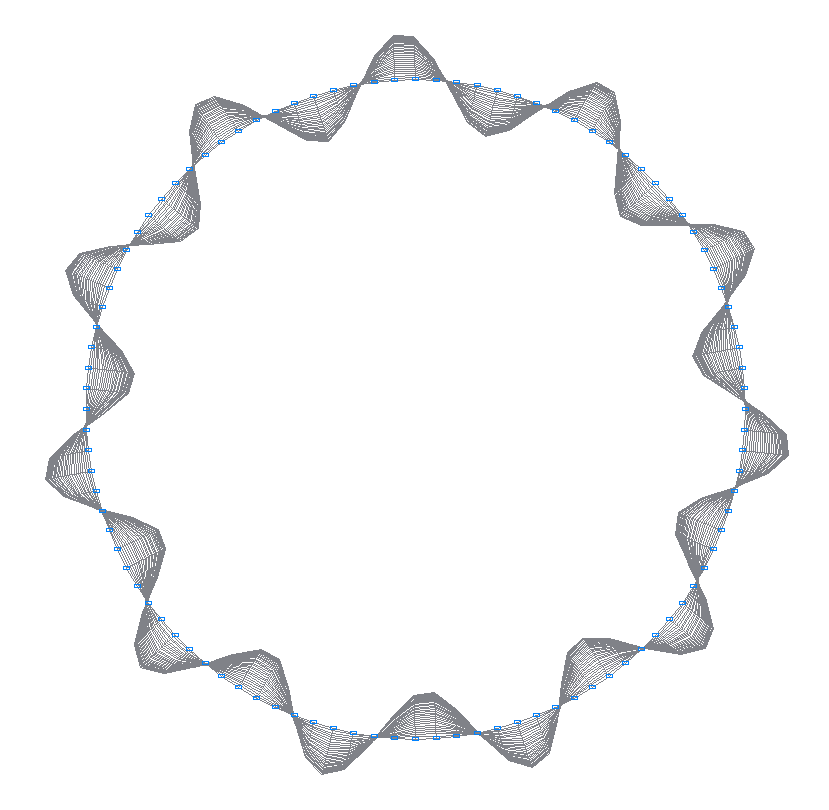
40-th (39-th theoretical) natural oscillation mode
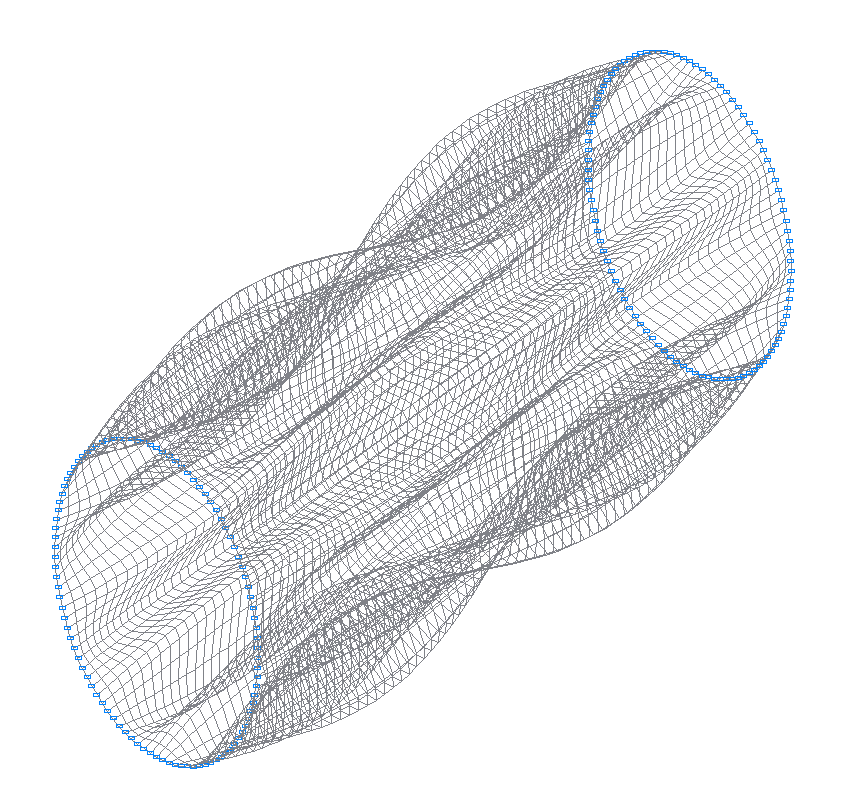
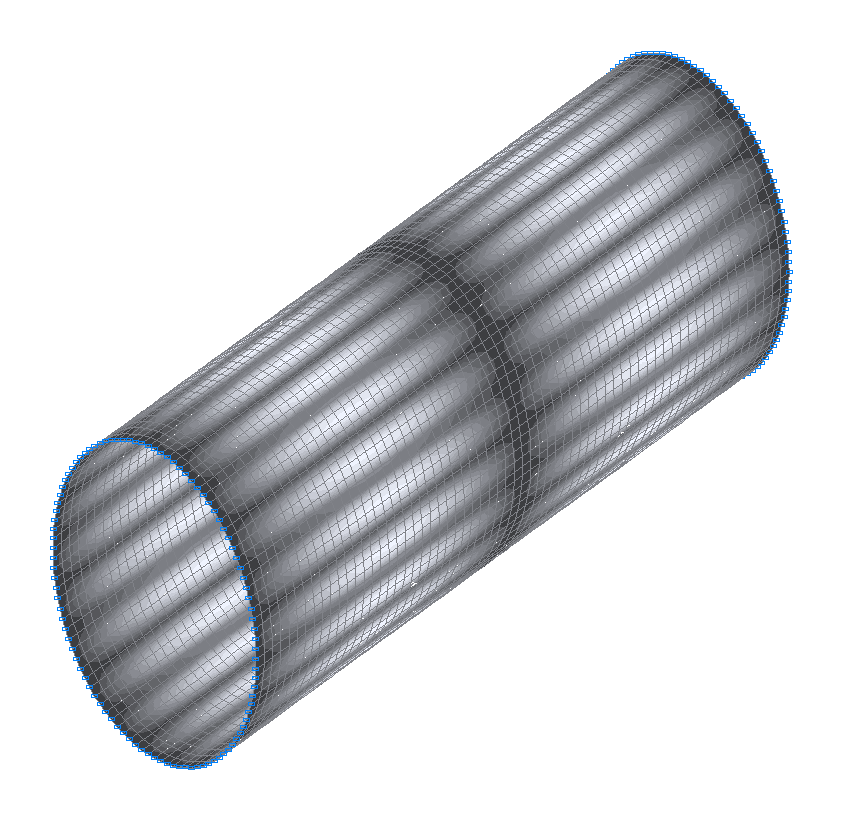

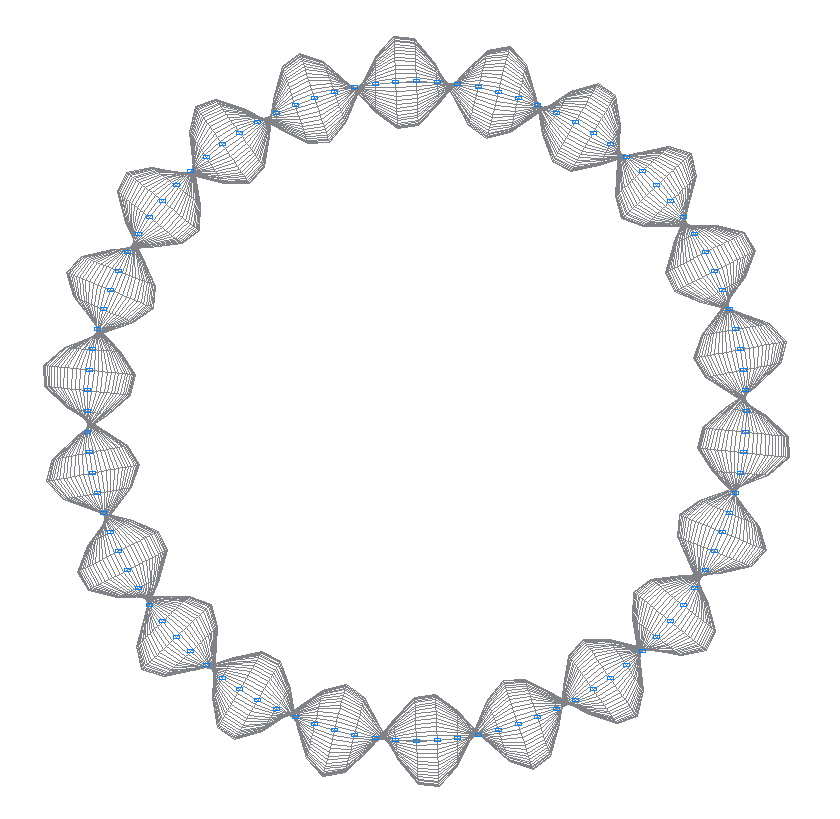
42-nd (41-st theoretical) natural oscillation mode
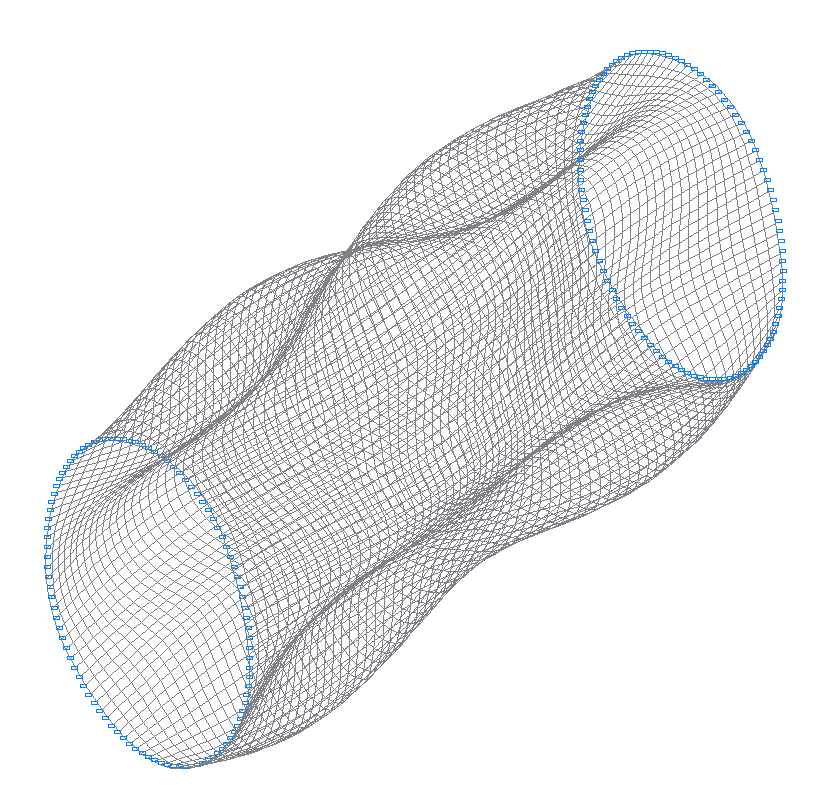

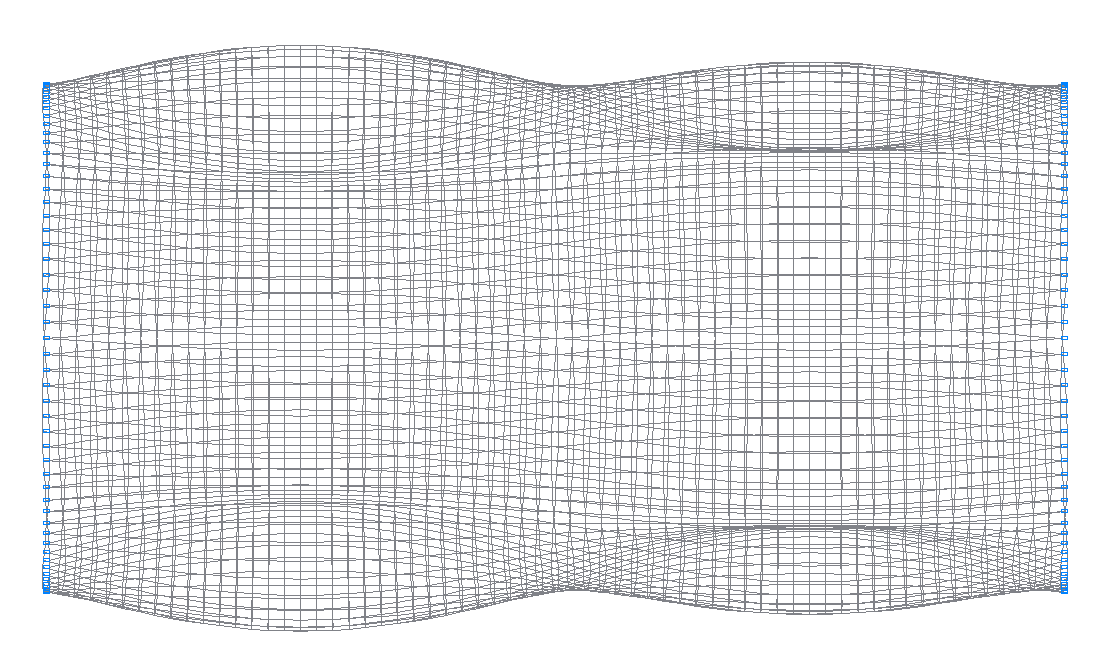
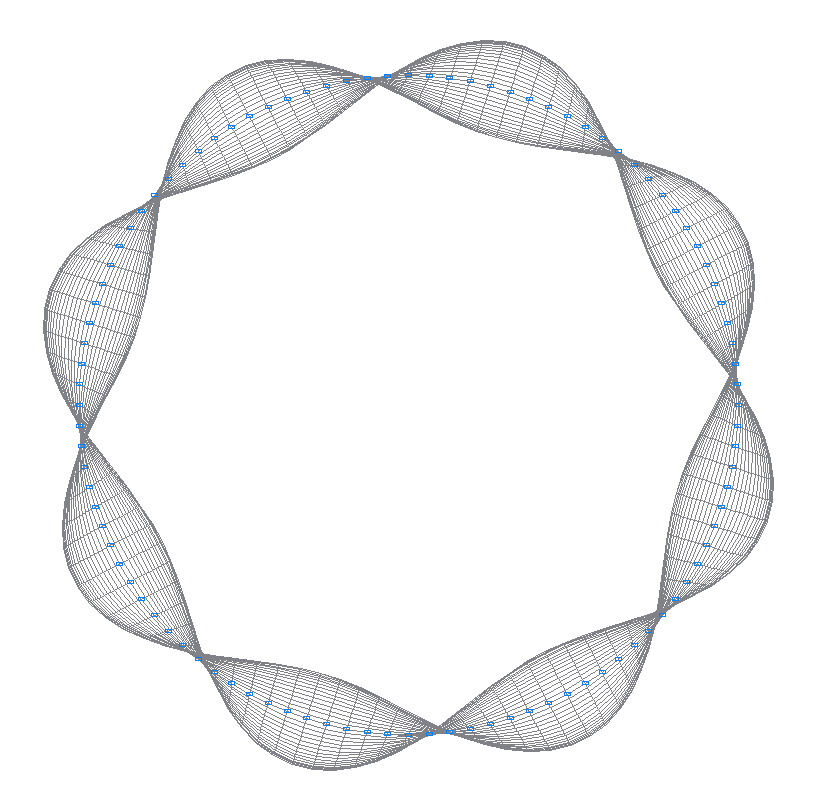
44-th (43-rd theoretical) natural oscillation mode
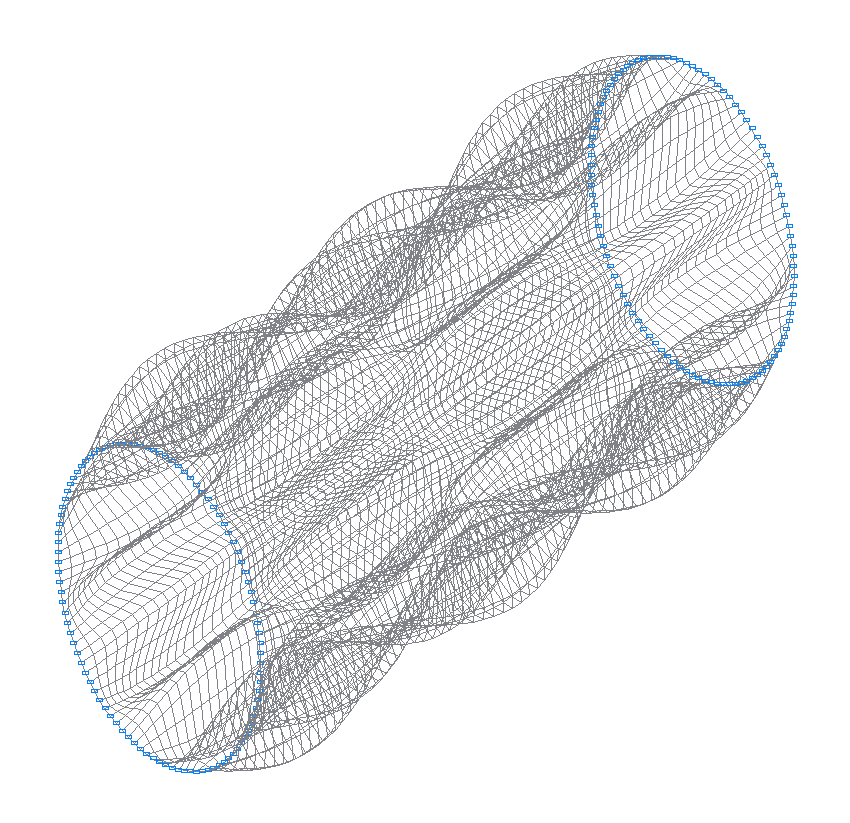
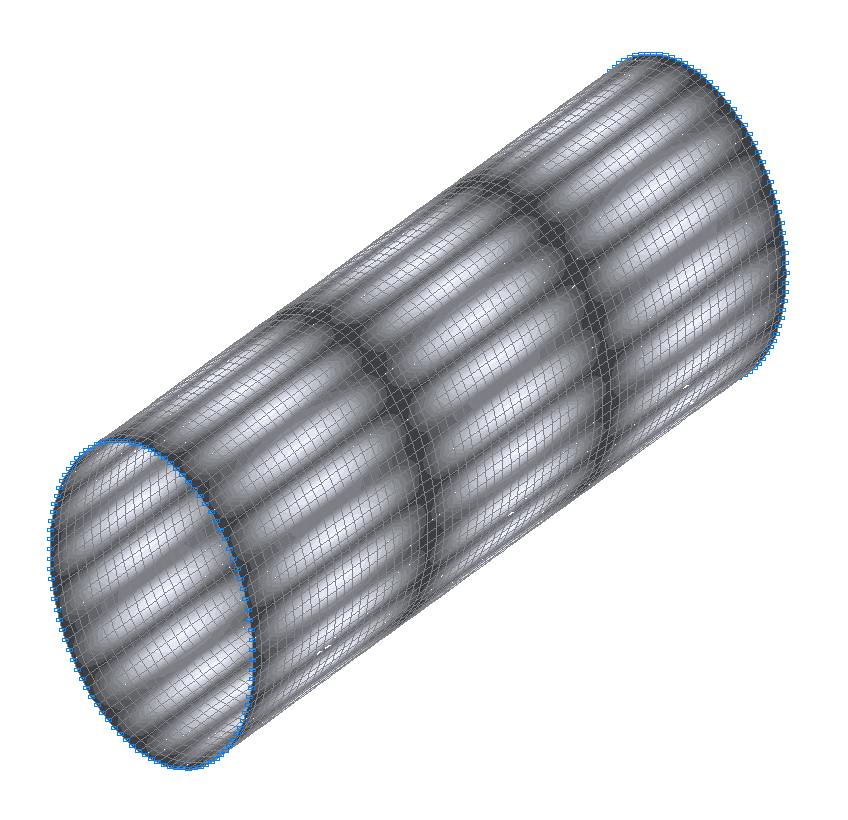
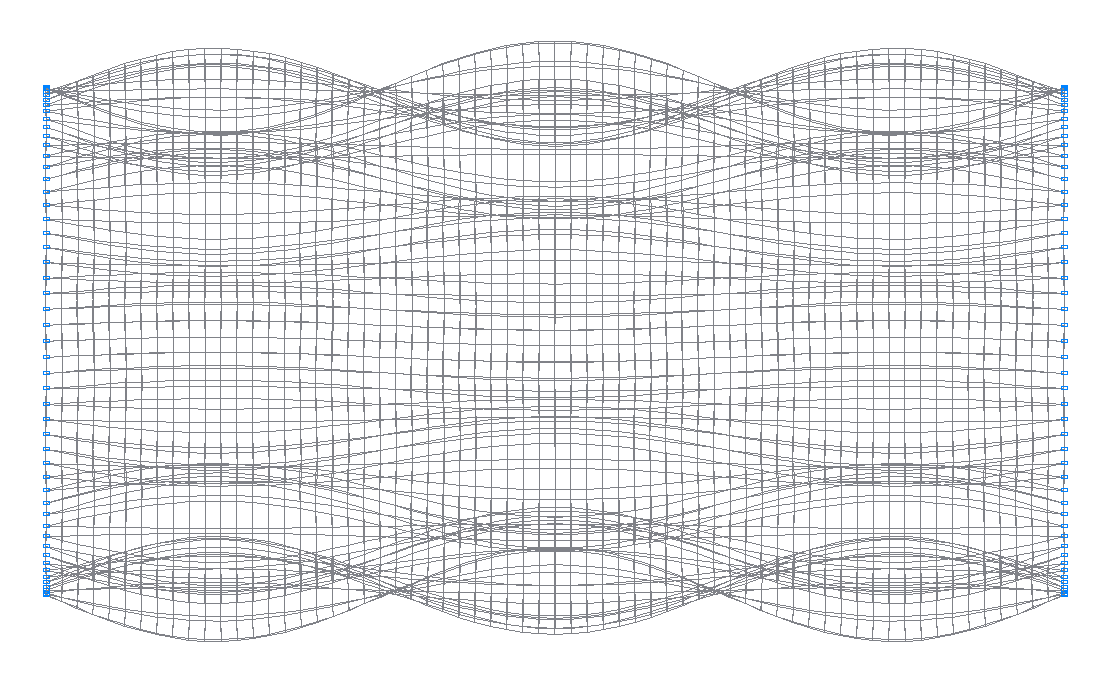
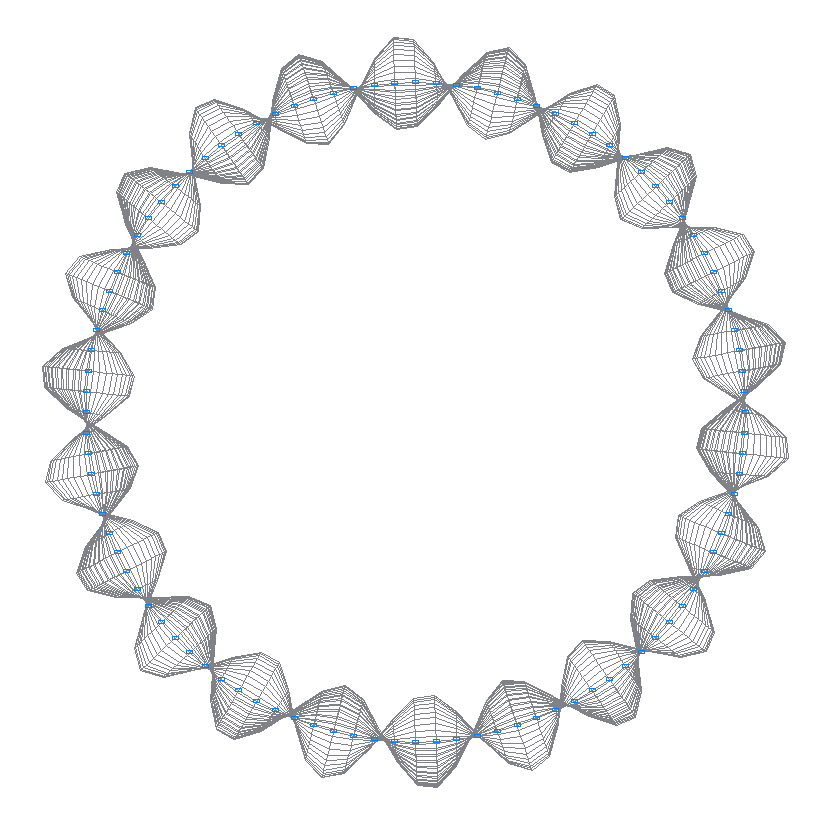
46-th (45-th theoretical) natural oscillation mode
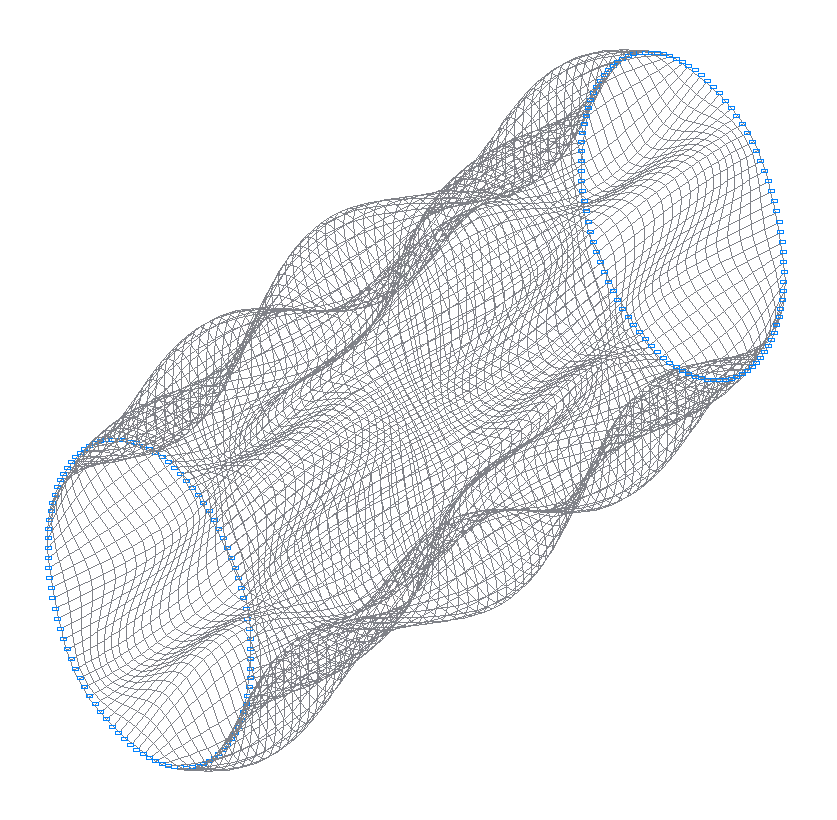
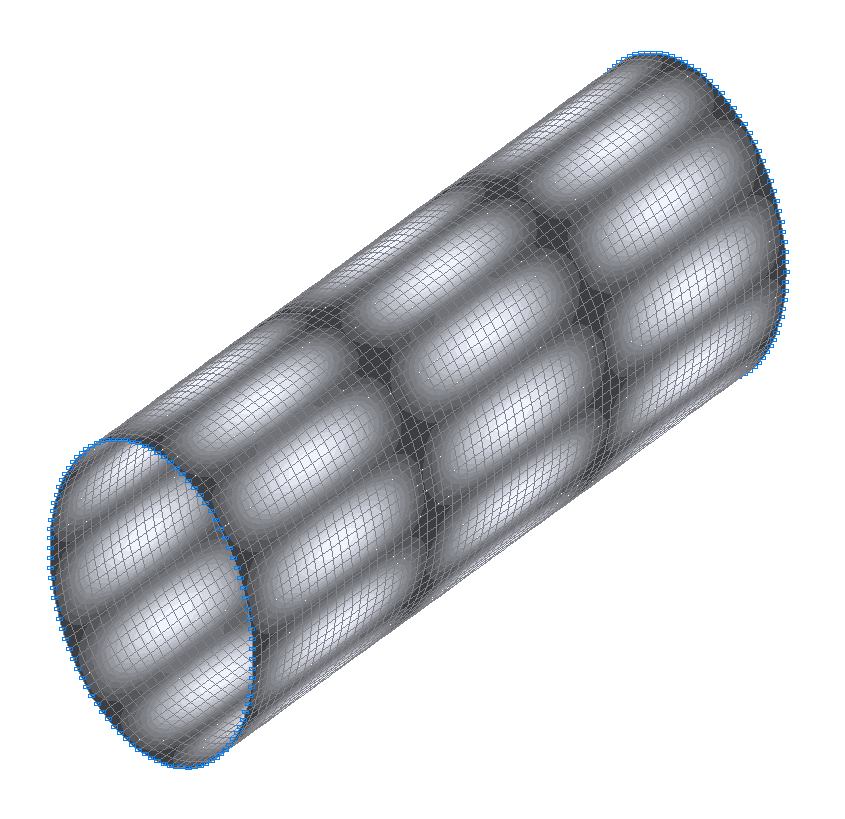
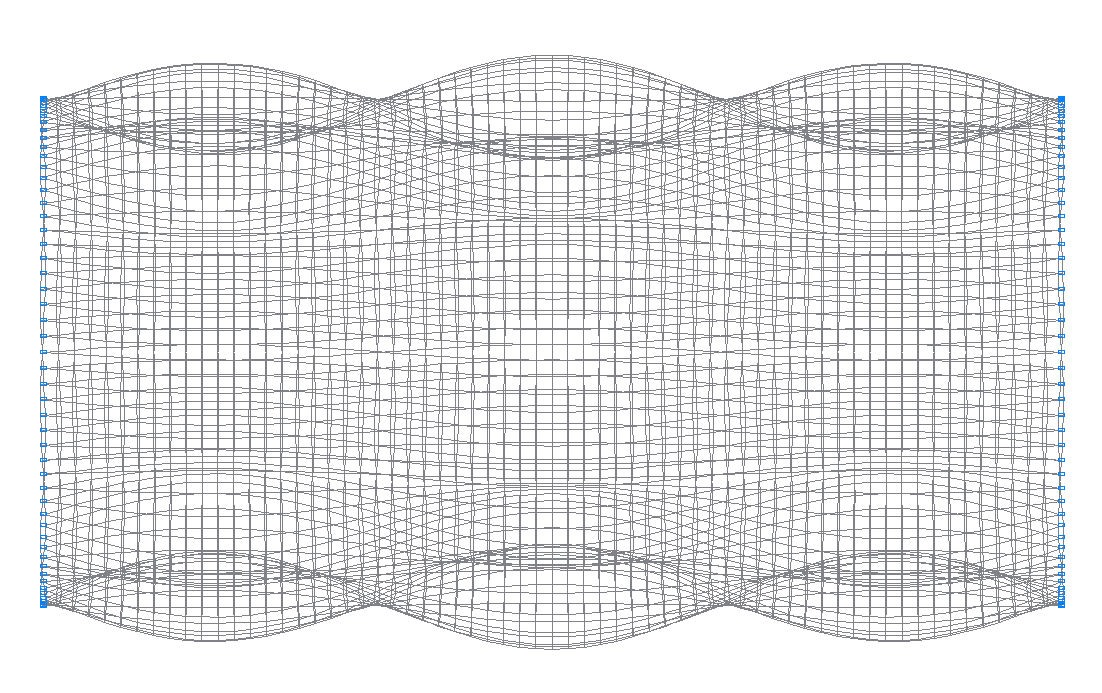
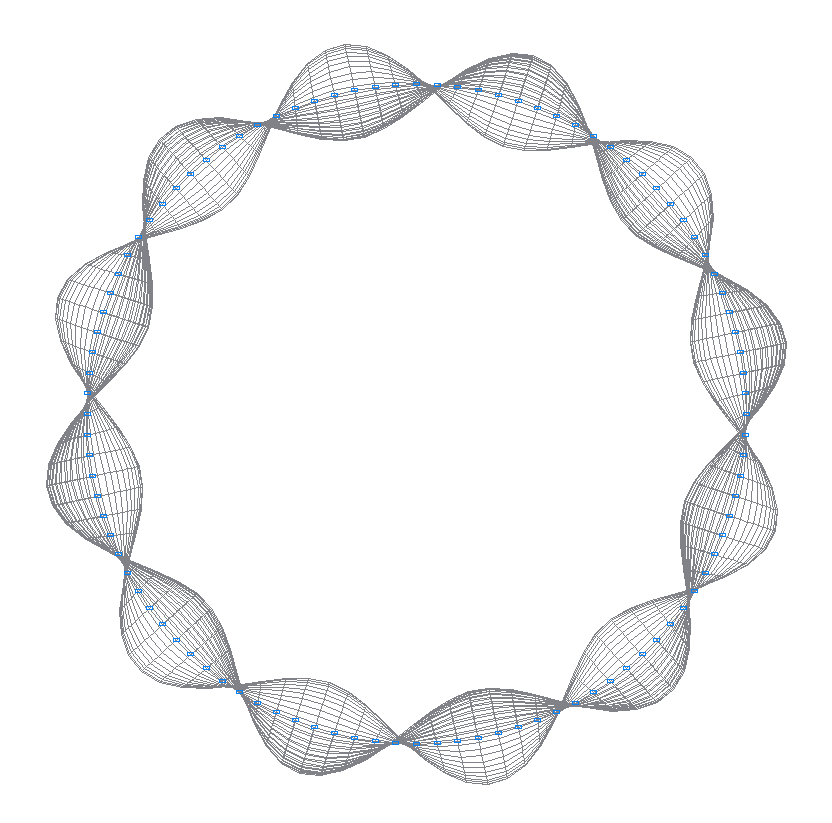
48-th (47-th theoretical) natural oscillation mode
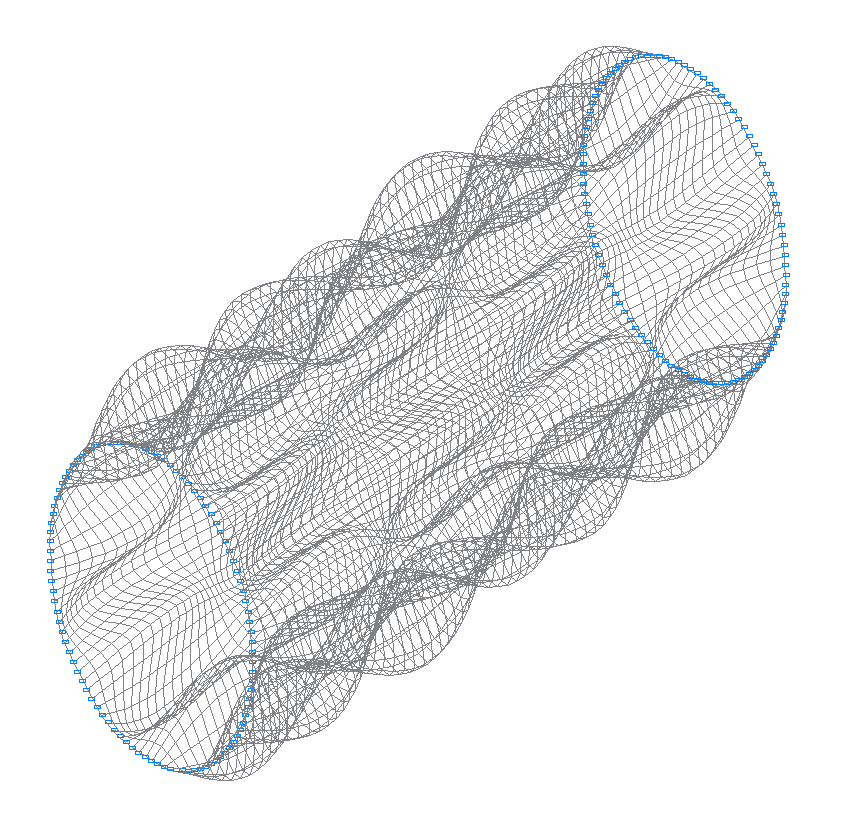
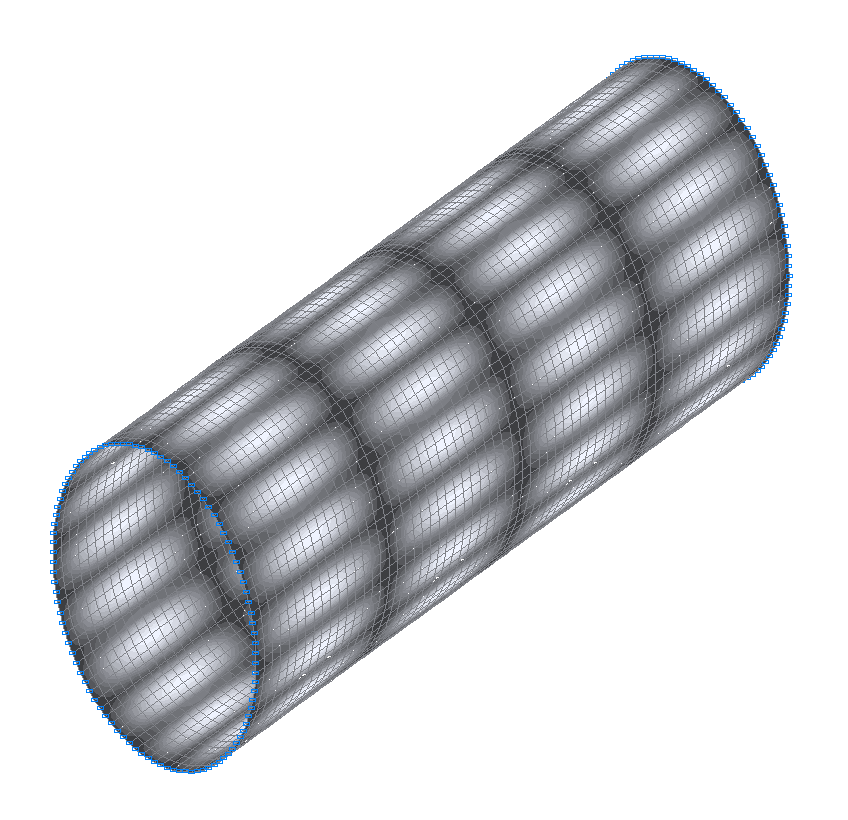
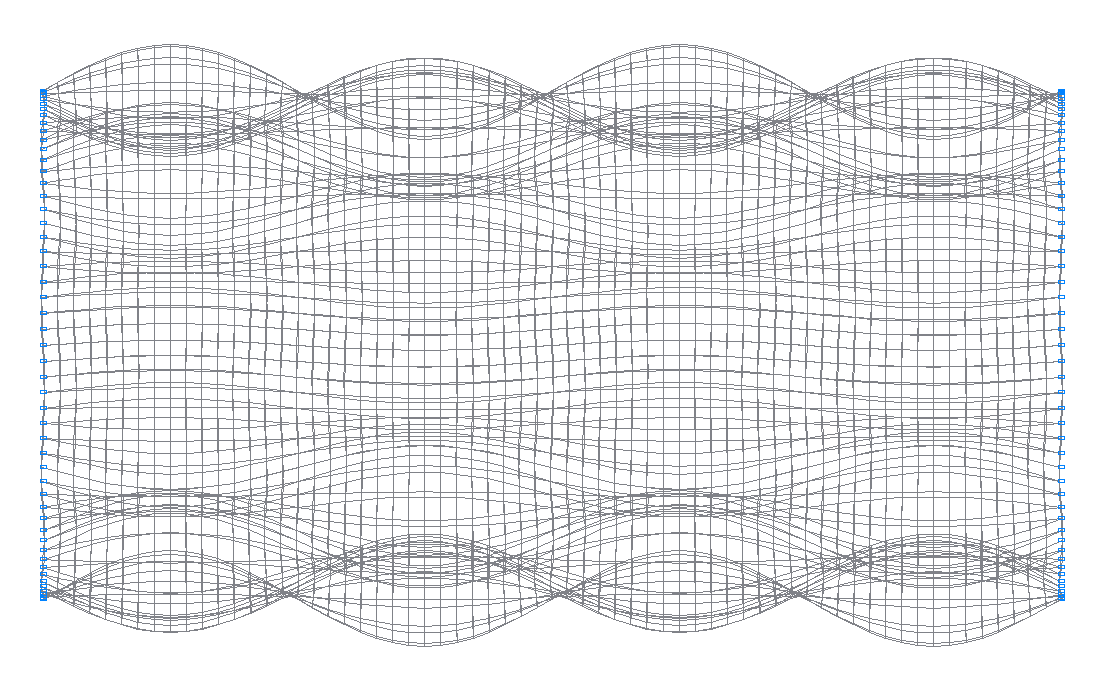
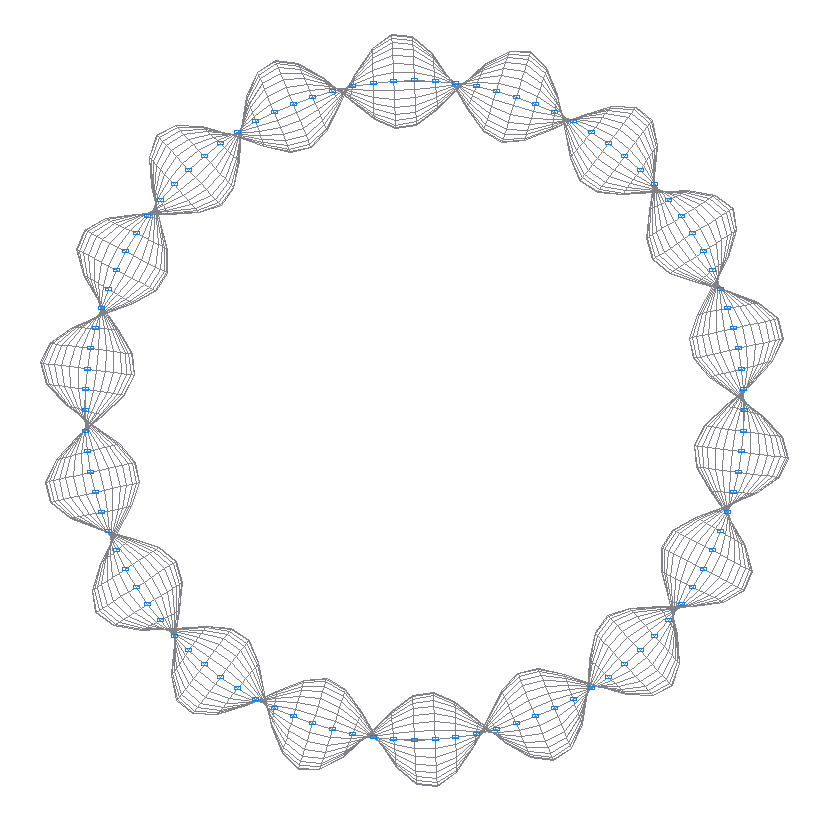
50-th (49-th theoretical) natural oscillation mode
Comparison of solutions:
Natural frequencies ω, Hz
|
Oscillation mode |
Number of nodal circles m and meridians n |
Theory |
SCAD |
Deviations, % |
|---|---|---|---|---|
|
1, 2 |
2, 5 |
354.4 |
354.9 |
0.14 |
|
3, 4 |
2, 6 |
408.3 |
408.9 |
0.15 |
|
5, 6 |
2, 4 |
409.5 |
410.1 |
0.15 |
|
7, 8 |
2, 7 |
522.1 |
522.9 |
0.15 |
|
9, 10 |
2, 3 |
642.1 |
642.8 |
0.11 |
|
11, 12 |
2, 8 |
671.1 |
672.0 |
0.13 |
|
13, 14 |
3, 7 |
723.2 |
724.9 |
0.24 |
|
15, 16 |
3, 6 |
768.5 |
770.3 |
0.23 |
|
17, 18 |
3, 8 |
784.3 |
785.9 |
0.20 |
|
19, 20 |
2, 9 |
846.2 |
847.3 |
0.13 |
|
21, 22 |
3, 9 |
914.9 |
916.6 |
0.19 |
|
23, 24 |
3, 5 |
962.3 |
964.5 |
0.23 |
|
25, 26 |
2, 10 |
1044.3 |
1045.7 |
0.13 |
|
27, 28 |
3, 10 |
1090.7 |
1092.5 |
0.17 |
|
29, 30 |
4, 8 |
1095.6 |
1099.3 |
0.34 |
|
31, 32 |
4, 9 |
1115.7 |
1119.2 |
0.31 |
|
33, 34 |
4, 7 |
1194.2 |
1198.2 |
0.33 |
|
35, 36 |
4, 10 |
1223.2 |
1226.5 |
0.27 |
|
37, 38 |
2, 2 |
1241.3 |
1242.5 |
0.10 |
|
39, 40 |
2, 11 |
1264.3 |
1265.9 |
0.13 |
|
41, 42 |
3, 11 |
1299.1 |
1301.2 |
0.16 |
|
43, 44 |
3, 4 |
1368.6 |
1370.9 |
0.17 |
|
45, 46 |
4, 11 |
1391.6 |
1395.0 |
0.24 |
|
47, 48 |
4, 6 |
1444.4 |
1448.8 |
0.30 |
|
49, 50 |
5, 9 |
1470.4 |
1477.2 |
0.46 |
|
51, 52 |
5, 10 |
1474.4 |
1480.6 |
0.42 |
|
53, 54 |
2, 12 |
1505.8 |
1507.5 |
0.11 |
|
55, 56 |
3, 12 |
1534.3 |
1536.6 |
0.15 |
|
57, 58 |
5, 11 |
1570.6 |
1576.5 |
0.38 |
|
59, 60 |
5, 8 |
1584.6 |
1591.9 |
0.46 |
|
61, 62 |
4, 12 |
1603.7 |
1607.1 |
0.21 |
|
63, 64 |
5, 12 |
1735.5 |
1741.2 |
0.33 |
|
65, 66 |
2, 13 |
1768.5 |
1770.3 |
0.10 |
|
67, 68 |
3, 13 |
1793.5 |
1795.9 |
0.13 |
|
69, 70 |
6, 10 |
1837.2 |
1848.0 |
0.59 |
|
71, 72 |
5, 7 |
1842.3 |
1850.1 |
0.42 |
|
73, 74 |
6, 11 |
1844.3 |
1854.3 |
0.54 |
|
75, 76 |
4, 13 |
1849.2 |
1852.7 |
0.19 |
|
77, 78 |
4, 5 |
1892.8 |
1897.7 |
0.26 |
|
79, 80 |
6, 12 |
1942.4 |
1951.9 |
0.49 |
|
81, 82 |
6, 9 |
1942.8 |
1954.3 |
0.59 |
|
83, 84 |
5, 13 |
1951.0 |
1956.7 |
0.29 |
|
85, 86 |
2, 14 |
2052.3 |
2054.1 |
0.09 |
|
87, 88 |
3, 14 |
2075.2 |
2077.7 |
0.12 |
|
89, 90 |
6, 13 |
2111.1 |
2120.1 |
0.43 |
|
91, 92 |
4, 14 |
2122.7 |
2126.3 |
0.17 |
|
93, 94 |
3, 3 |
2137.0 |
2140.0 |
0.14 |
|
95, 96 |
6, 8 |
2181.3 |
2193.4 |
0.55 |
|
97, 98 |
5, 14 |
2205.6 |
2211.2 |
0.25 |
|
99, 100 |
7, 11 |
2199.6 |
2215.4 |
0.72 |
|
101, 102 |
7, 12 |
2223.0 |
2237.8 |
0.67 |
|
103, 104 |
5, 6 |
2275.4 |
2283.7 |
0.36 |
|
105, 106 |
7, 10 |
2281.7 |
2298.3 |
0.73 |
|
107, 108 |
7, 13 |
2333.3 |
2347.3 |
0.60 |
|
109, 110 |
6, 14 |
2333.8 |
2342.5 |
0.37 |
|
111, 112 |
2, 15 |
2357.2 |
2358.9 |
0.07 |
|
113, 114 |
3, 15 |
2378.9 |
2381.2 |
0.10 |
|
115, 116 |
4, 15 |
2421.3 |
2424.8 |
0.14 |
|
117, 118 |
7, 9 |
2485.9 |
2503.2 |
0.70 |
|
119, 120 |
5, 15 |
2492.0 |
2497.5 |
0.22 |
|
121, 122 |
7, 14 |
2512.8 |
2526.3 |
0.54 |
|
123, 124 |
8, 12 |
2565.0 |
2586.6 |
0.84 |
|
125, 126 |
6, 7 |
2574.4 |
2586.9 |
0.49 |
|
127, 128 |
6, 15 |
2598.7 |
2607.3 |
0.33 |
|
129,130 |
8, 13 |
2613.1 |
2633.7 |
0.79 |
|
131, 132 |
8, 11 |
2614.4 |
2637.0 |
0.86 |
|
133, 134 |
4, 4 |
2630.0 |
2635.4 |
0.21 |
|
135, 136 |
2, 16 |
2683.2 |
2684.5 |
0.05 |
|
137, 138 |
3, 16 |
2704.1 |
2706.1 |
0.07 |
|
139, 140 |
8, 14 |
2742.8 |
2762.4 |
0.71 |
|
141, 142 |
4, 16 |
2743.2 |
2746.5 |
0.12 |
|
143, 144 |
7, 15 |
2747.0 |
2759.9 |
0.47 |
|
145, 146 |
8, 10 |
2776.0 |
2799.3 |
0.84 |
|
147, 148 |
5, 16 |
2806.0 |
2811.3 |
0.19 |
|
149, 150 |
2, 1 |
2832.3 |
2835.3 |
0.11 |
Notes: In the analytical solution the natural frequencies ω of the simply supported circular cylindrical shell with the density of the material ρ can be determined from the characteristic equation:
\[\left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{3}\cdot \omega^{6}+K2\cdot \left( {\frac{4\cdot \pi ^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)^{2}\cdot \omega^{4}+K1\cdot \left( {\frac{4\cdot \pi^{2}\cdot \rho \cdot R^{2}\cdot \left( {1-\nu^{2}} \right)}{E}} \right)\cdot \omega ^{2}+K0=0, \quad where:\quad \] \[ K2=-1-\frac{1}{2}\cdot \left( {3-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]-\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}+2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right\} \] \[ {\begin{array}{*{20}c} {K1=\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}+\frac{1}{2}\cdot \left( {3-\nu -2\cdot \nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot n^{2}+} \\ {\frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\frac{1}{2}\cdot \left( {3-\nu } \right)\cdot \left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{3}} \right.+2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}-\left( {2-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{2}-\frac{1}{2}\left( {3+\nu } \right)\cdot n^{4}+} \\ {\left. {2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right\} +\frac{h^{4}}{144\cdot R^{4}}\cdot \left\{ {2\cdot \left( {1-\nu } \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{6}+\left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{2}} \right\}} \\ \end{array} } \] \[ {\begin{array}{*{20}c} {K0=-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}-\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \frac{h^{2}}{12\cdot R^{2}}\cdot \left\{ {\left[ {\left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{4}-2\cdot \left( {4-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{2}-} \right.} \\ {\left. {8\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{4}-2\cdot n^{6}+4\cdot \left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}+4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{2}\cdot n^{2}+n^{4}} \right\} -} \\ {\frac{1}{2}\cdot \left( {1-\nu } \right)\cdot \frac{h^{4}}{144\cdot R^{4}}\cdot \left\{ {4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{8}-4\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{6}\cdot n^{2}+\left( {1-\nu^{2}} \right)\cdot \left( {\frac{\left( {m-1} \right)\cdot \pi \cdot R}{L}} \right)^{4}\cdot n^{4}} \right\}} \\ \end{array} } \]
m=2,3,4, ... - number of nodal lines in the circumferential direction, taking into account the lines along the end support contours,
n=0,1,2, ...- number of pairs of nodal lines in the meridian direction when each pair is located on one diameter.
