Natural Oscillations of a Cantilever Open Cylindrical Shell
Objective: Modal analysis of a cantilever open cylindrical shell.
Initial data file: 5.9.spr
Problem formulation: Determine the natural oscillation modes and frequencies ω of the cantilever open cylindrical shell with the density of the material ρ.
References: Olson M. D., Lindberg G. M., Vibration analysis of cantilevered curved plates using a new cylindrical shell finite element, Second conference on matrix methods in structural mechanics at Wright – Patterson Air Force Base in Ohio, AFFDL-TR-68-155, 1969, p. 247-269.
Initial data:
| E = 30.0·106 PSI = 2.0685·108 kPa | - elastic modulus; |
| ν = 0.3 | - Poisson’s ratio; |
| ρ = 0.28386 lb/in3 = 7.8572 t/m3 | - density of the material; |
| h = 0.12 in = 3.048·10-3 м | - thickness of the cylindrical shell; |
| R = 24 in = 0.6096 m | - radius of the midsurface of the cylindrical shell; |
| L = 12 in = 0.3048 m | - length of the generatrix of the cylindrical shell; |
| W =12 in = 0.3048 m | - length of the arc of the director of the cylindrical shell. |
Finite element model: Design model – general type system, 400 four-node shell elements of type 50. The spacing of the finite element mesh in the meridian and in the circumferential directions is 0.01524 m (20 elements). Boundary conditions of the clamped curvilinear edge are provided by imposing constraints in the directions of all linear and angular displacements (degrees of freedom X, Y, Z, UX, UY, UZ). The distributed mass is specified by transforming the static load from the self-weight of the cylindrical shell: ow = γ∙h, where γ = ρ∙g = 77.0791 kN/m3. Number of nodes in the design model – 441. The determination of the natural oscillation modes and natural frequencies is performed by the Lanczos method. A consistent mass matrix is used in the calculation.
Results in SCAD
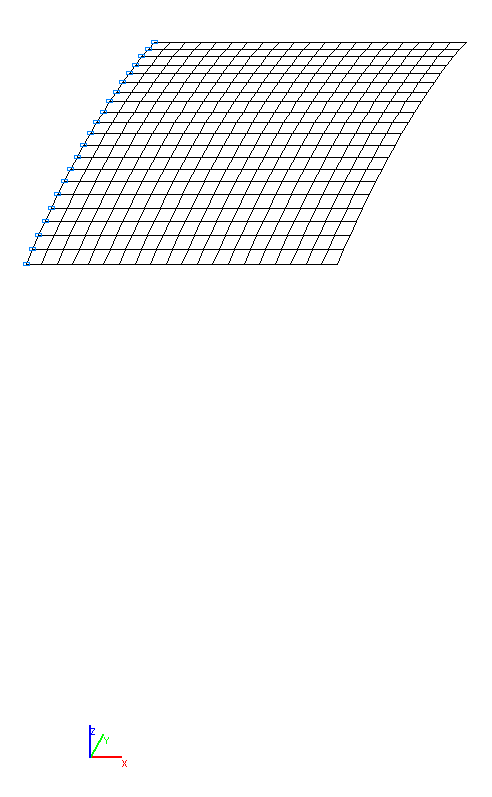

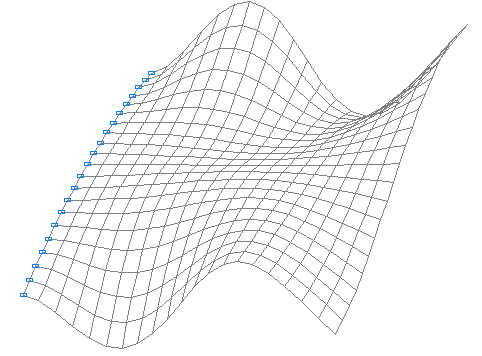
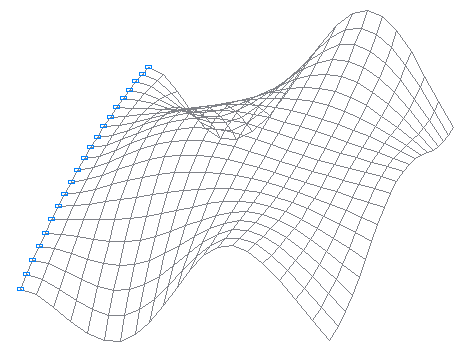
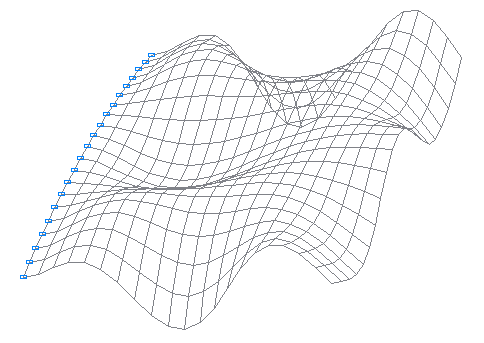
Design model


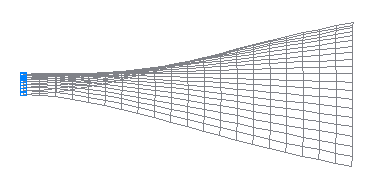
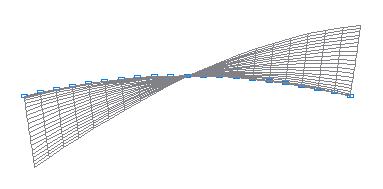
1-st natural oscillation mode



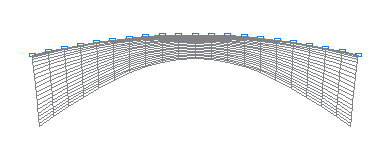
2-nd natural oscillation mode


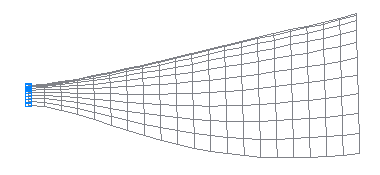

3-rd natural oscillation mode


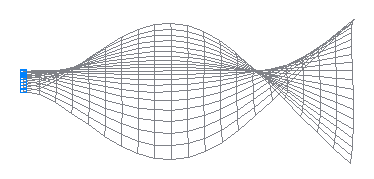
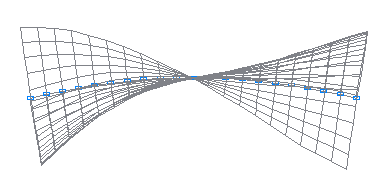
4-th natural oscillation mode
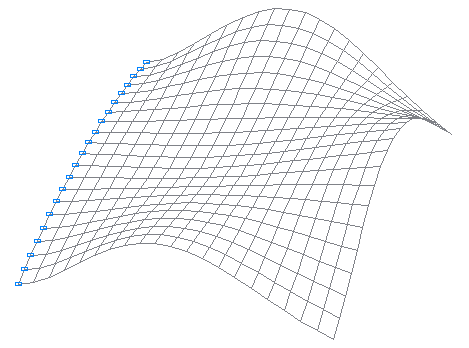

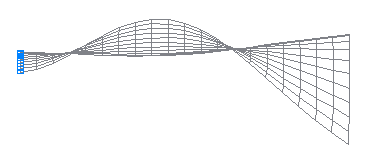
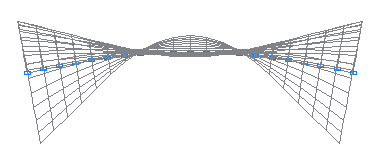
5-th natural oscillation mode


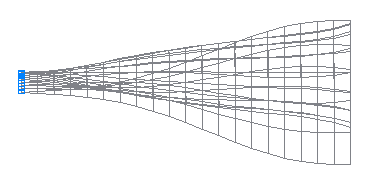
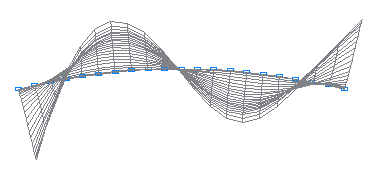
6-th natural oscillation mode
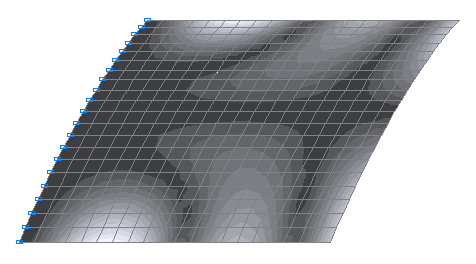
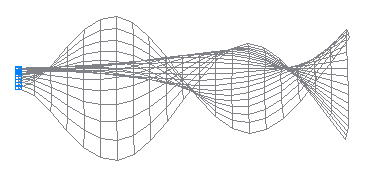
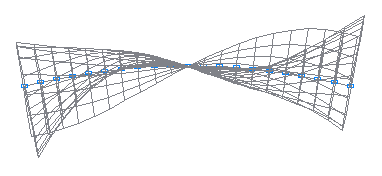
7-th natural oscillation mode
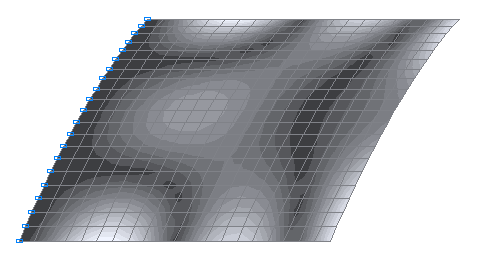
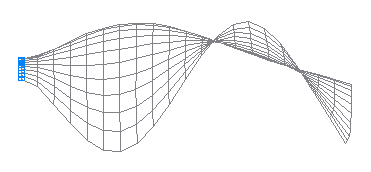
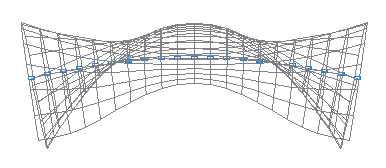
8-th natural oscillation mode
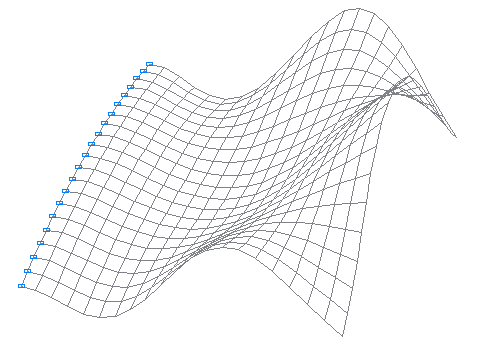

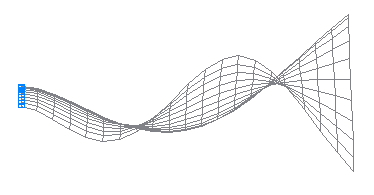
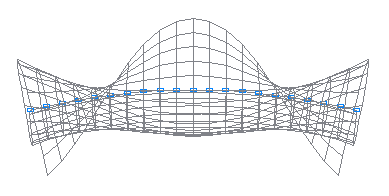
9-th natural oscillation mode


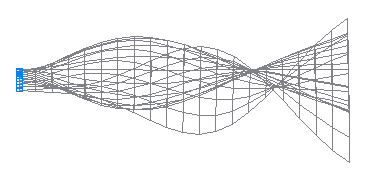
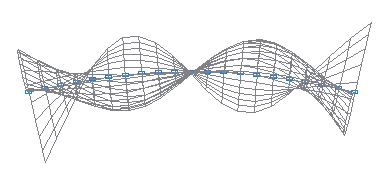
10-th natural oscillation mode
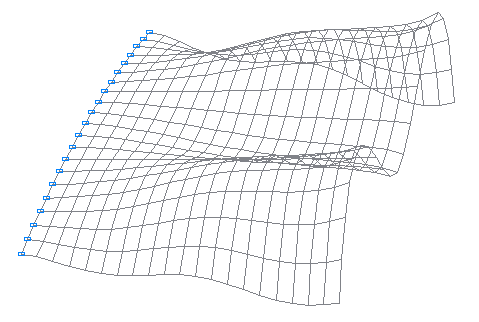

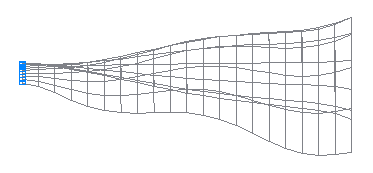
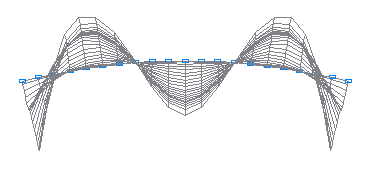
11-th natural oscillation mode

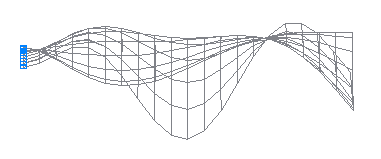
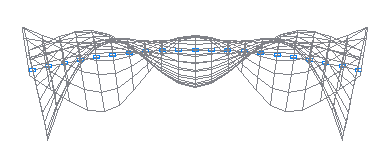
12-th natural oscillation mode
Comparison of solutions:
Natural frequencies ω, Hz
|
Oscillation mode |
Nodal lines |
Experiment |
SCAD |
Deviations, % |
|---|---|---|---|---|
|
1 |
|
85.6 |
86,2 |
0,35 |
|
2 |
|
135.5 |
139,2 |
0,57 |
|
3 |
|
258.9 |
248,2 |
0,95 |
|
4 |
|
350.6 |
344,2 |
0,75 |
|
5 |
|
395.2 |
388,2 |
0,89 |
|
6 |
|
531.1 |
529,9 |
1,39 |
|
7 |
|
743.2 |
730,9 |
1,33 |
|
8 |
|
751.2 |
732,9 |
1,22 |
|
9 |
|
792.1 |
776,5 |
0,87 |
|
10 |
|
809.2 |
805,4 |
1,21 |
|
11 |
|
996.8 |
999,1 |
1,97 |
|
12 |
|
1215.0 |
1210,5 |
1,85 |












