Stability of a Three-Span Two-Storey Frame Subjected to Concentrated Longitudinal Forces Applied to the Columns in the Joints with Girders
Objective: Determination of the critical value of the concentrated longitudinal forces acting on the columns of a three-span two-storey frame in the joints with the girders corresponding to the moment of its buckling.
Initial data file: 6.1.spr
Problem formulation: The three-span two-storey frame is subjected to the action of concentrated longitudinal forces P applied to the columns in the joints with the girders. The beam-to-column and column-to-foundation joints are rigid. The axial stiffness values of the girders and columns are assumed to be significant in order to exclude their effect on the solution of the problem. Determine the critical value of the concentrated longitudinal forces Pcr, corresponding to the moment of buckling of the frame.
References: N. V. Kornoukhov, Strength and Stability of Framework Structures, Moscow, Stroyizdat Publ., 1949, p. 259.
Initial data:
| L = 8.0 m | - length of the girders of the frame; |
| H = 4.0 m | - height of the columns of the frame; |
| EA = 1.0·1010 kN | - axial stiffness of the structural members of the frame; |
| EIС1 = 8.00·105 kN∙m2 | - bending stiffness of the columns of the first storey; |
| iС1 = EIС1/H = 2.0·105 kN∙m | - bending stiffness of the columns of the first storey per running meter; |
| EIС2 = 4.00·105 kN∙m2 | - bending stiffness of the columns of the second storey; |
| iС2 = EIС2/H = 1.00·105 kN∙m | - bending stiffness of the columns of the second storey per running meter; |
| EIР1 = 13.28·105 kN∙m2 | - bending stiffness of the girders of the first storey; |
| iР1 = EIР1/L = 1.66·105 kN∙m | - bending stiffness of the girders of the first storey per running meter; |
| EIР2 = 8.00·105 kN∙m2 | - bending stiffness of the girders of the second storey; |
| iР2 = EIР2/L = 1.00·105 kN∙m | - bending stiffness of the girders of the second storey per running meter; |
| P = 1.0·105 kN | - initial value of the concentrated longitudinal forces on the columns of the frame in the joints with the girders. |
Finite element model: Design model – plane frame, 80 elements of type 2. The spacing of the finite element mesh along the longitudinal axes of the structural members (along the X1 axes of the local coordinate systems) is 1.0 m. Boundary conditions are provided by imposing constraints on the support nodes of the frame in the directions of the degrees of freedom X, Z, UY. The action with the initial value of the concentrated longitudinal forces P is specified in the beam-to-column joints. Number of nodes in the design model – 78.
Results in SCAD
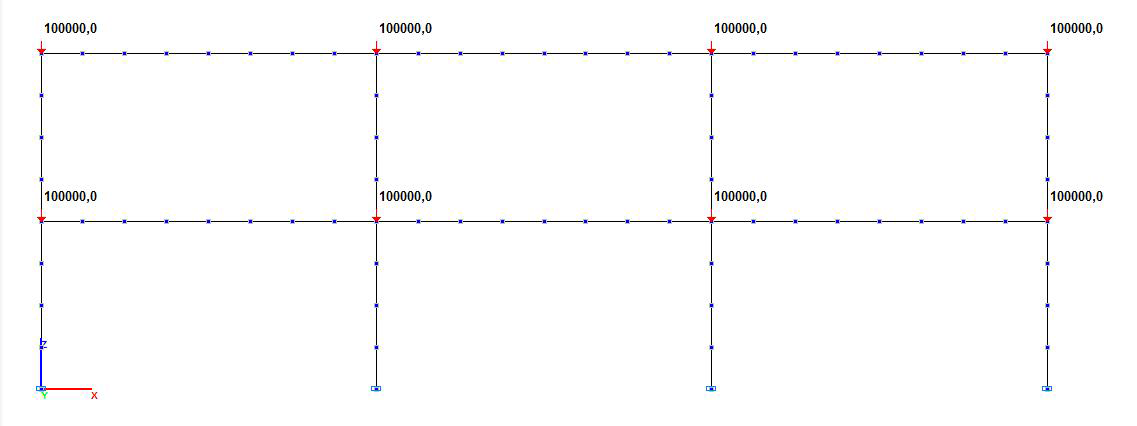
Design model
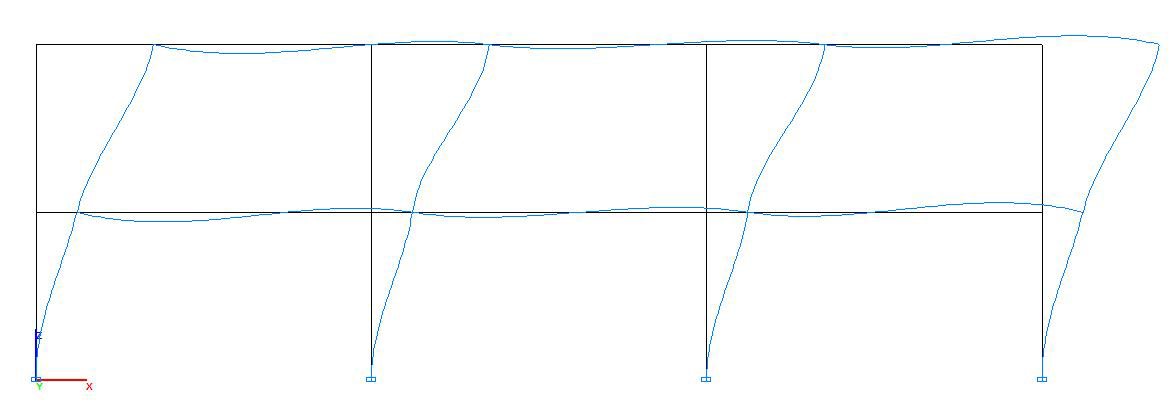
Buckling mode
Comparison of solutions:
|
Parameter |
Theory |
SCAD |
Deviation, % |
|
Critical value of the concentrated longitudinal forces Pcr, kN |
156250 |
1.5625∙100000 = = 156250 |
0.00 |
Notes: In the analytical solution the critical value of the concentrated longitudinal forces Pcr, corresponding to the moment of buckling of the frame can be determined according to the following formula:
\[ P_{cr} =2.5000^{2}\cdot \frac{i_{С1} }{H}. \]
