Stability of a Circular Two-Hinged Arch of a Constant Cross-Section Subjected to Hydrostatic Pressure
Objective: Determination of the critical value of the hydrostatic pressure applied to a circular two-hinged arch of a constant cross-section corresponding to the moment of its buckling.
Initial data files:
|
File name |
Description |
|---|---|
|
Design model with the central angle of the arc 2∙ω = 2∙30 ° |
|
|
Design model with the central angle of the arc 2∙ω = 2∙90 ° |
Problem formulation: The circular two-hinged arch of a constant cross-section is subjected to the action of the uniformly distributed radial load q. Determine the critical value of the uniformly distributed radial load qcr, corresponding to the moment of buckling of the arch. It is assumed that when the arch buckles, the load elements follow the axis of the arch staying parallel to their former directions, and therefore the displacement of the pressure line takes place at the buckling of the arch. Compare the result of the calculation with the solution (S.P. Timoshenko), when the load action lines do not change at the distortion of the arch axis and the pressure line does not move at the buckling of the arch.
References: N. V. Kornoukhov, Strength and Stability of Framework Structures, Moscow, Stroyizdat Publ., 1949, p. 212.
Initial data:
| R = 60.0 m (120.0 m) | - radius of the longitudinal axis of the arch; |
| 2∙ω = 2∙90 ° (2∙30 °) | - central angle of the arc; |
| EA = 2.16·106 kN | - axial stiffness of the arch; |
| EI = 2.592·105 kN∙m2 | - bending stiffness of the arch; |
| q = 1.0 kN/m | - initial value of the uniformly distributed radial load on the arch. |
Finite element model: Design model – plane frame, 36 elements of type 2. The arch is divided into finite elements along its longitudinal axis (along the X1 axes of the local coordinate systems) by the step of the central angle of 5.0 ° (1.667 °). Boundary conditions are provided by imposing constraints on the support nodes of the arch in the directions of the degrees of freedom X, Z. The action with the initial value of the uniformly distributed radial load q is specified in the directions opposite to the Z1 axes of the local coordinate systems of the elements. Number of nodes in the design model – 37.
Results in SCAD
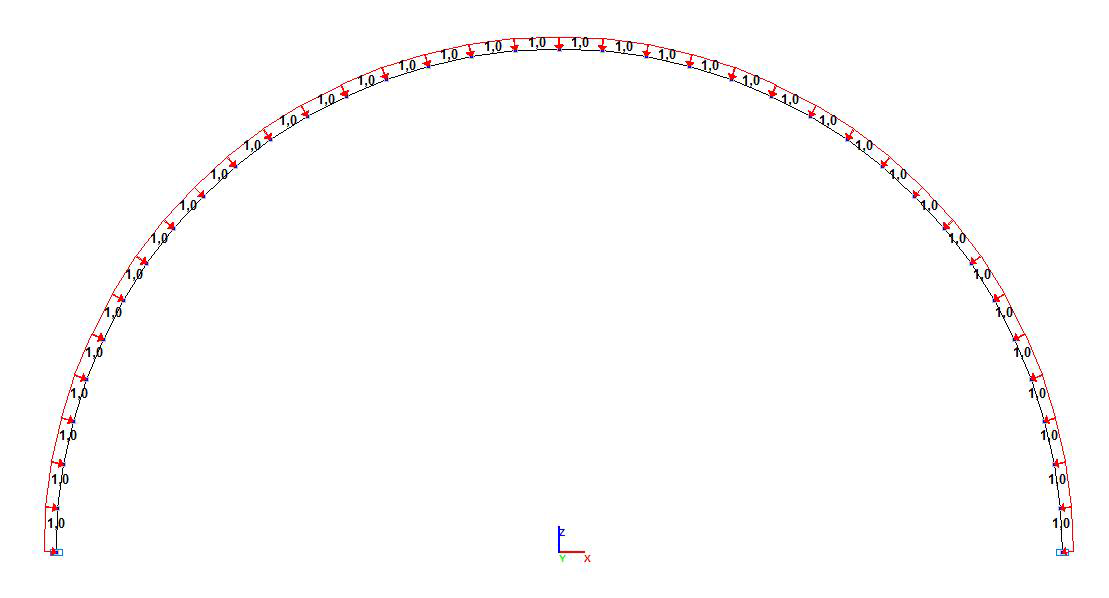
Design model with the central angle of the arc 2∙90 °
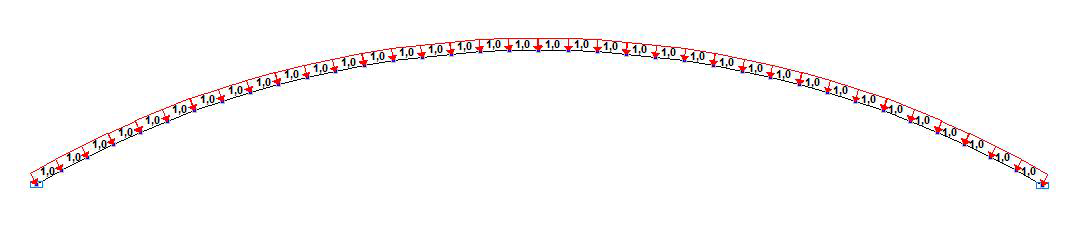
Design model with the central angle of the arc 2∙30 °
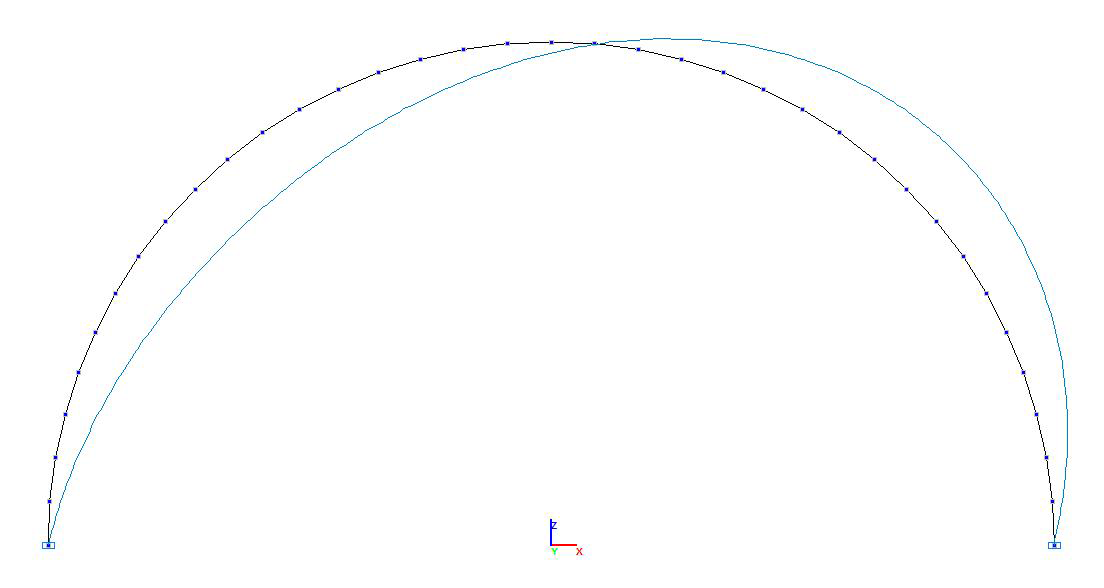
Buckling mode for the model with the central angle of the arc 2∙90 °
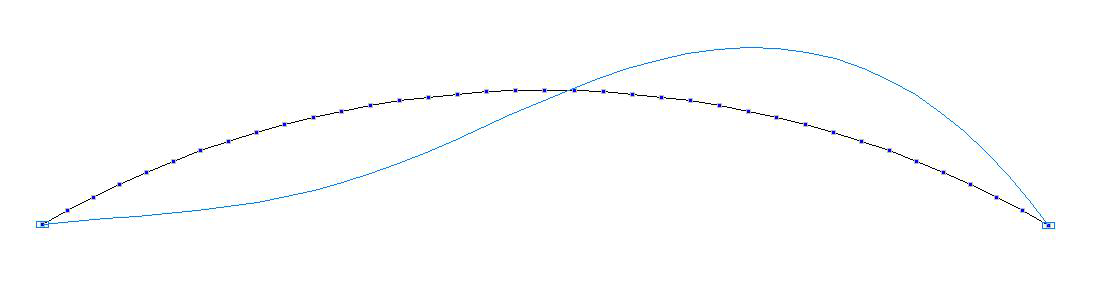
Buckling mode for the model with the central angle of the arc 2∙30 °
Comparison of solutions:
Critical value of the uniformly distributed radial load on the arch qcr, kN/m
|
Design model |
Theory |
SCAD |
Deviation, % |
|---|---|---|---|
|
with the central angle of the arc 2∙90 ° |
3.925 (3.600) [3.932] |
3.933914∙1.0 = = 3.934 |
0.23 (9.28) [0.05] |
|
with the central angle of the arc 2∙30 ° |
5.391 (5.250) [5.392] |
5.393093∙1.0 = = 5.393 |
0.04 (2.72) [0.02] |
Theoretical values calculated according to the conditions of this example (according to N. V. Kornoukhov) are given without brackets;
Theoretical values calculated according to the conditions of S. P. Timoshenko are given in round brackets;
Theoretical values calculated for a two-hinged frame made up of 2∙m=36 equal chords inscribed in an arc of a circle and subjected to the action of equal radial forces in all its nodes are given in square brackets.
Notes: In the analytical solution according to the conditions of N. V. Kornoukhov the critical value of the uniformly distributed radial load qcr, corresponding to the moment of buckling of the arch can be determined according to the following formula:
\[ q_{cr} =\eta^{2}\cdot \frac{EI}{R^{3}}, \]where η (critical load parameter) is determined by solving the transcendental equation:
\[ \frac{1}{\left( {\eta^{2}-1} \right)^{2}}\cdot \left[ {\eta^{3}\cdot \left( {\omega +\frac{1}{2}\cdot \sin \left( {2\cdot \omega } \right)} \right)-\eta \cdot \left( {\omega +\frac{3}{2}\cdot \sin \left( {2\cdot \omega } \right)} \right)+\frac{1-\cos \left( {2\cdot \omega } \right)}{tg\left( {\eta \cdot \omega } \right)}} \right]=0. \]In the analytical solution according to the conditions of S. P. Timoshenko the critical value of the uniformly distributed radial load qcr, corresponding to the moment of buckling of the arch can be determined according to the following formula:
\[ q_{cr} =\frac{EI}{R^{3}}\cdot \left( {\frac{\pi^{2}}{\omega^{2}}-1} \right). \]In the analytical solution for a two-hinged frame made up of equal chords inscribed in an arc of a circle, the critical value of the uniformly distributed radial load qcr, corresponding to its moment of buckling can be determined according to the following formula:
\[ q_{cr} =2\cdot \upsilon^{2}\cdot \frac{EI}{L^{3}}\cdot \sin \left( {\frac{A}{2}} \right), \]where υ (critical load parameter) is determined by solving the transcendental equation:
\[ \left( {1-\frac{\sin \left( \upsilon \right)}{\upsilon }\cdot \frac{1-\cos \left( A \right)}{\cos \left( \upsilon \right)-\cos \left( A \right)}} \right)\cdot \left( {m+\frac{\sin \left( {2\cdot m\cdot A} \right)}{2\cdot \sin \left( A \right)}} \right)+\left( {\frac{2\cdot \sin \left( {\frac{A}{2}} \right)\cdot \sin \left( {\frac{\upsilon }{2}} \right)}{\cos \left( \upsilon \right)-\cos \left( A \right)}\cdot \frac{\sin \left( \upsilon \right)}{\upsilon }\cdot \frac{\sin \left( {m\cdot A} \right)}{\sin \left( {m\cdot \upsilon } \right)}} \right)\cdot \left( {\frac{\sin \left( {m\cdot \left( {A+\upsilon } \right)} \right)}{2\cdot \sin \left( {\frac{A+\upsilon }{2}} \right)}+\frac{\sin \left( {m\cdot \left( {A-\upsilon } \right)} \right)}{2\cdot \sin \left( {\frac{A-\upsilon }{2}} \right)}} \right)=0. \]
2∙m - number of chords of the frame,
A - central angle of one chord of the frame,
L - length of one chord of the frame:
\[ L=R\cdot \sqrt {2\cdot \left( {1-\cos \left( A \right)} \right)} . \]
