Stability of a Cylindrical Thin-Walled Shell with Simply Supported Edges Subjected to Uniform External Pressure

Objective: Determination of the critical value of the external pressure uniformly distributed over the lateral surface of a cylindrical thin-walled shell with simply supported edges corresponding to the moment of its buckling.

 

Initial data file: 6.11_S.spr

Problem formulation: The cylindrical thin-walled shell with simply supported edges is subjected to the action of the uniform external pressure q. Determine the critical value of the uniform external pressure qcr, corresponding to the moment of buckling of the cylindrical thin-walled shell.

References: E.I. Grigolyuk, V.V. Kabanov, Stability of Shells, Moscow, Nauka, 1978, p. 137.

A.S. Volmir. Stability of Deformable Systems, Moscow, Nauka, 1967, p. 545.

Initial data:

E = 2.0·108 kPa	- elastic modulus of the shell material;
ν = 0.3	- Poisson’s ratio;
h = 0.005 m	- thickness of the shell;
R = 0.5 m	- radius of the midsurface of the shell;
L = 1.0 m	- length of the shell;
q = 1.0·103 kPa	- initial value of the external pressure.

 

 

Finite element model: Design model – general type system, 1200 four-node shell elements of type 50. The spacing of the finite element mesh in the meridian direction is 0.05 m (20 elements) and in the circumferential is 6.0º (60 elements). Boundary conditions of the simply supported edges are provided by imposing constraints in the directions of the linear displacements in their plane (degrees of freedom Y, Z). The dimensional stability of the design model is provided by imposing constraints of finite rigidity (60 elements of type 51) in the nodes of the cross-section on the symmetry plane of the cylindrical shell in the meridian direction (k_x = 1.0 kN/m). The uniformly distributed load (along the Z1 axis of the local coordinate system) with the initial value q = 1.0·10³ kPa is specified on the lateral surface of the cylindrical shell. Number of nodes in the design model – 1260.

 

Results in SCAD

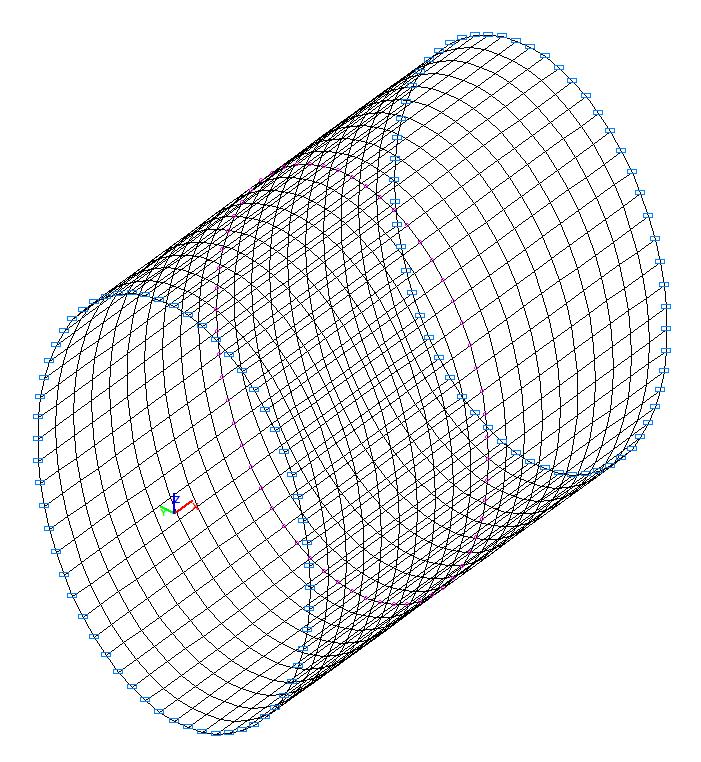
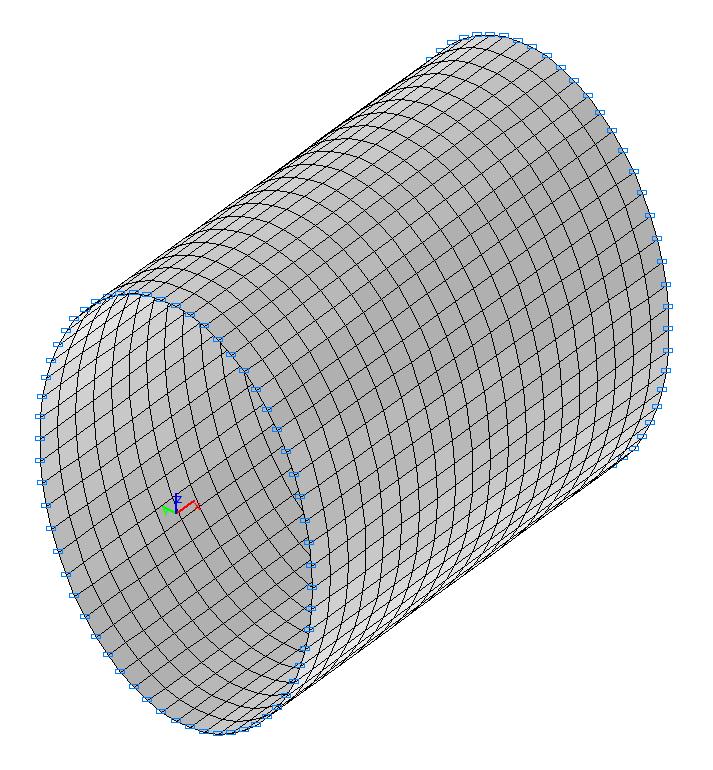
Design model

 

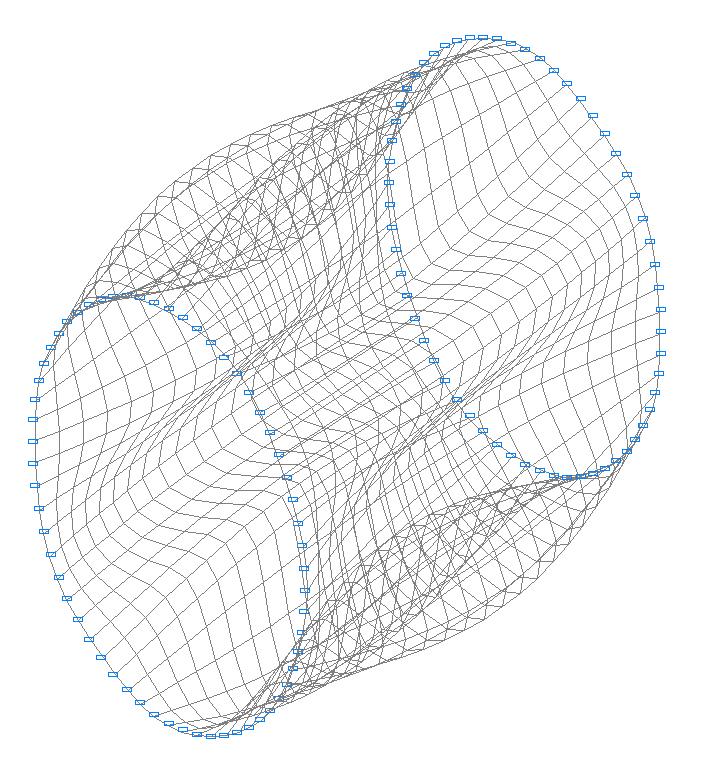
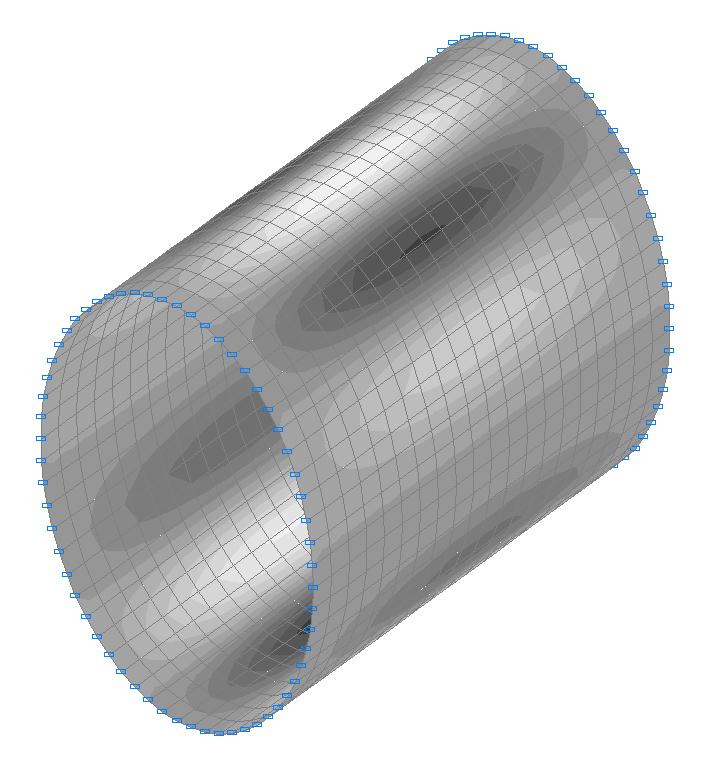
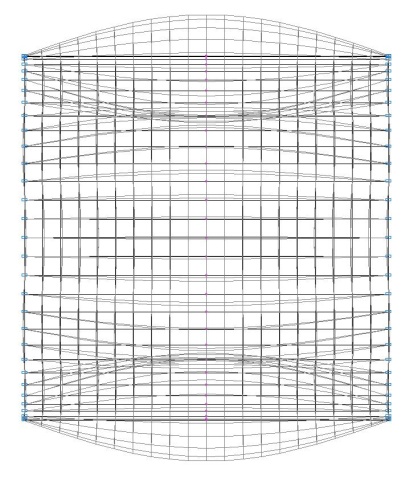
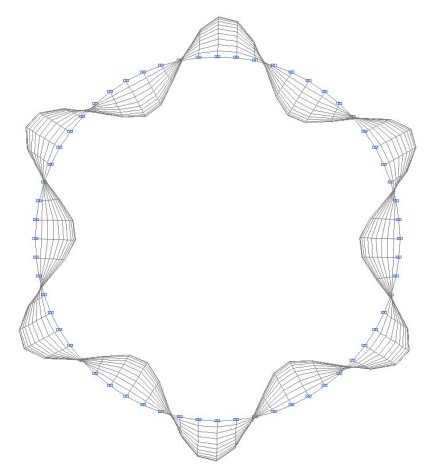
1-st buckling mode

 

Comparison of solutions:

Critical value of the uniform external pressure qcr, kPa

Buckling mode	Number of half waves in the meridian direction m and number of waves in the circumferential n direction	Theory	SCAD	Deviation, %
1	1; 6	981 (917)	0.999898 ∙1000 = = 1000	1.94 (9.05)

Theoretical values calculated according to the shallow shell theory for the membrane initial state are given without brackets;
Theoretical values calculated according to the general shell theory for the membrane initial state are given in round brackets.

 

Notes: In the analytical solution the critical value of the uniform external pressure qcr, corresponding to the moment of buckling of the cylindrical thin-walled shell is determined in accordance with the shallow shell theory by the following formula:

\[ q_{cr} =\frac{E\cdot h}{R\cdot n^{2}}\cdot \frac{\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{4}}{\left[ {\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}}+\frac{D}{R^{3}\cdot n^{2}}\cdot \left[ {\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}, \quad where: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]

 

In the analytical solution the critical value of the uniform external pressure q_cr, corresponding to the moment of buckling of the cylindrical thin-walled shell is determined in accordance with the general shell theory on the basis of the condition of equality to zero of the determinant of the system of governing equations:

\[ \left| {{\begin{array}{*{20}c} {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+\frac{1-\nu }{2}\cdot n^{2}+\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } & {\frac{1+\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)\cdot n} & {\nu \cdot \left( {\frac{\pi \cdot R}{L}} \right)} \\ {\frac{1+\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)\cdot n} & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}} \right)\cdot \left( {\frac{1-\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)-\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)} \right)\cdot n} \\ {\nu \cdot \left( {\frac{\pi \cdot R}{L}} \right)} & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)} \right)\cdot n} & {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)^{2}-\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } \\ \end{array} }} \right|=0 \]