Contact with Detachment for a Layer and Subgrade with a Concentrated Shear Force Applied to the Layer
Objective: Determination of the size of a contact area of a layer with the subgrade, when a concentrated shear force is applied to the layer, in the structurally nonlinear formulation.
Initial data file: Contact_3_731.spr
Problem formulation: The elastic layer of height b lies on the elastic subgrade with the possibility of slipping and is subjected to the action of the concentrated shear force P applied to the upper surface. Determine the size of the area of contact of the layer with the subgrade 2∙c.
References: K. Johnson, Mechanics of Contact Interaction, Moscow, Mir, 1989, p. 163
Initial data:
| E1 = 21.0·107 kN/m2 | - elastic modulus of the layer material; |
| ν1 = 0.3 | - Poisson’s ratio of the layer material; |
| E3 = 3.0·107 kN/m2 | - elastic modulus of the subgrade material; |
| ν3 = 0.2 | - Poisson’s ratio of the subgrade material; |
| b = 1.00 m | - height of the layer; |
| L = 10.00 m | - length of the layer and subgrade in the model; |
| H = 10.00 m | - height of the subgrade in the model; |
| P = 1000 kN | - value of the concentrated force applied to the upper surface of the layer. |
Finite element model: Design model – plane frame. Elements of the layer – 1000 eight-node grade beam elements of type 30. The spacing of the finite element mesh along the height and length of the layer is 0.1 m. Elements of the subgrade – 10000 eight-node grade beam elements of type 30. The spacing of the finite element mesh along the height and length of the subgrade is 0.1 m. 201 two-node elements of unilateral constraints of type 352 of increased stiffness k = 1.0·109 kN/m are introduced to model the contact with detachment between the lower surface of the layer and the upper surface of the subgrade. Each element vertically joins the nodes of the layer and the subgrade. Boundary conditions are provided by imposing constraints on the lower surface of the subgarde in the direction of the degree of freedom Z. The dimensional stability of the design model is provided by imposing constraints in the direction of the degree of freedom X along the vertical axis of symmetry of the layer and the subgrade (along the force P). The action is specified as a transverse nodal load P (in the direction of the Z axis of the global coordinate system). The nonlinear loading was generated for the incremental-iterative method with a loading factor - 1, number of steps - 1, number of iterations - 10 for the linear loading P. Number of nodes in the design model – 33622.
Results in SCAD
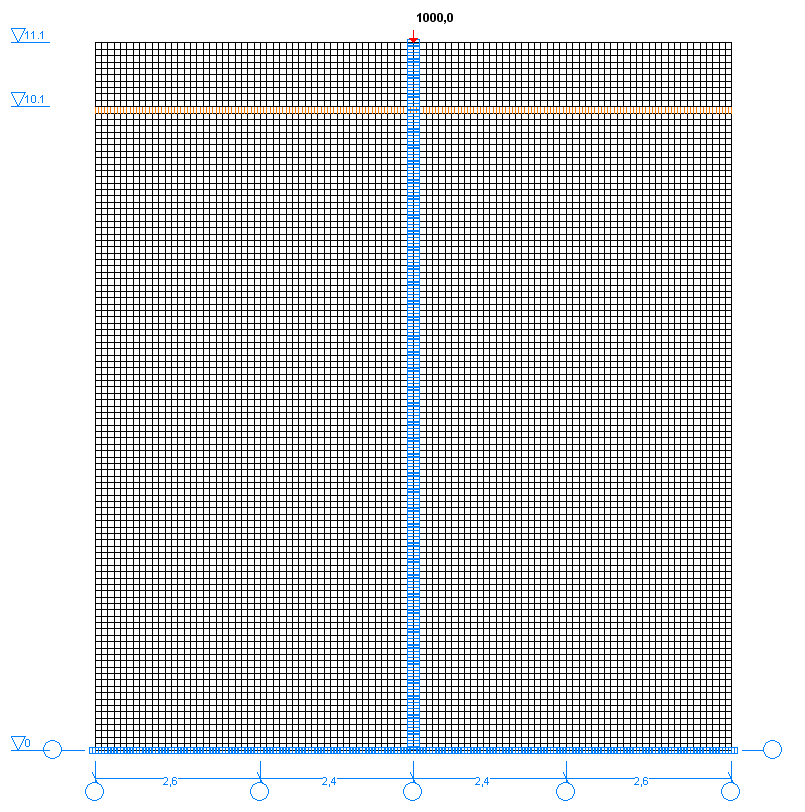
Design model

Deformed model
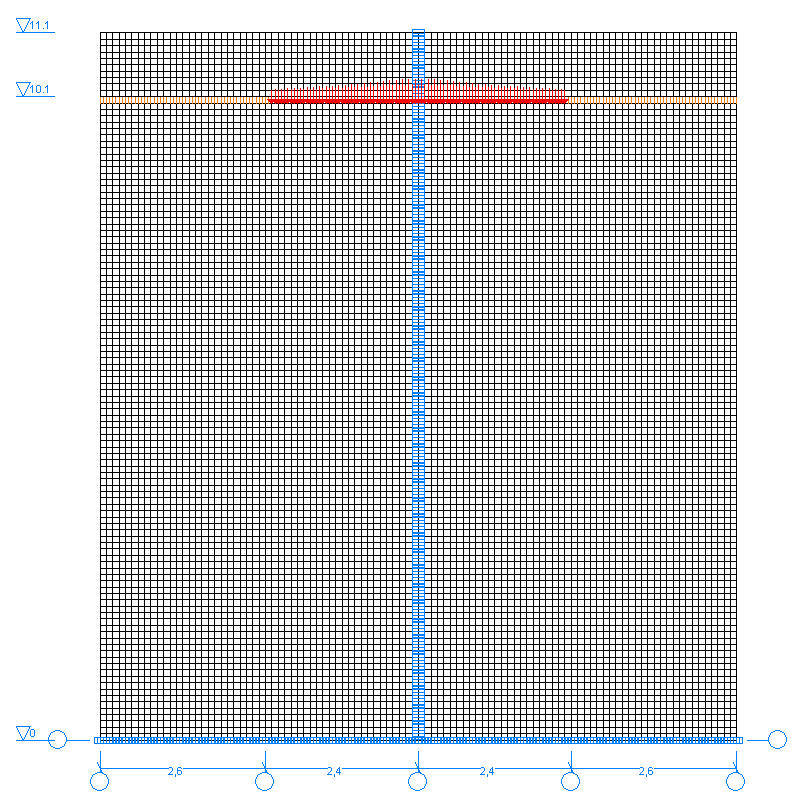
Area of contact with the subgrade, contact stresses
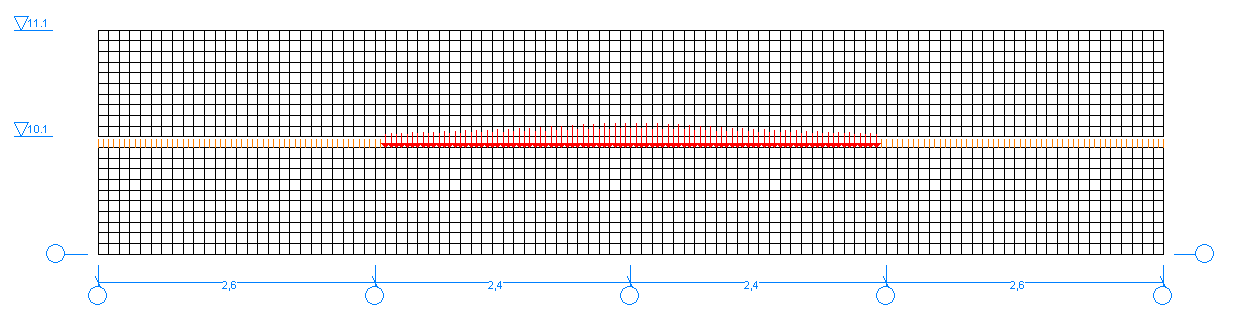
Area of contact with the subgrade, contact stresses (fragment of the model)
Comparison of solutions:
Area of contact with the subgrade 2∙c, m
|
Theory |
SCAD |
Deviation, % |
|---|---|---|
|
4.78 |
4.60 |
3.77 |
Notes: In the analytical solution the area of contact with the subgrade 2∙c can be determined according to the following formula:
\[ 2\cdot c=2\cdot b\cdot \sqrt[3]{1.845\cdot \frac{1-\nu_{3}^{2}}{E_{3} }\cdot \frac{E_{1} }{1-\nu_{1}^{2}}}. \]
