Плоская ферма под действием сосредоточенной силы

Цель: Определение напряженно-деформированного состояния плоской фермы от воздействия сосредоточенной силы.

Файл с исходными данными: SSLL09_v11.3.spr

Формулировка задачи: Плоская ферма состоит из двух наклонных нисходящих стержней одинаковой длины и жесткости поперечного сечения, расположенных симметрично относительно вертикальной оси, шарнирно соединенных в общем узле (точка C) и шарнирно опертых по противоположным узлам (точки A и B). В общем узле стержней фермы приложена вертикальная сосредоточенная сила F. Определить вертикальное перемещение общего узла стержней фермы Z и продольные силы в стержнях фермы N.

Ссылки: S. Timoshenko, Resistance des materiaux, t.1, Bruxelles, Edition Polytechnique Beranger, 1963, p. 10.

Исходные данные:

E = 2.1·1011  Па	- модуль упругости стержней фермы;
l = 4.5 м	- длина стержней фермы;
θ = 30º	- угол наклона стержней к горизонту;
A = 3.0·10-4 м2	- площадь поперечного сечения стержней;
F = 2.1·104 Н	- значение вертикальной сосредоточенной силы.

Конечноэлементная модель: Расчетная  схема – плоская шарнирно-стержневая система, 2 стержневых элемента типа 10. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Z для шарнирных опорных узлов. Количество узлов в расчетной схеме – 3.

Результаты решения в SCAD

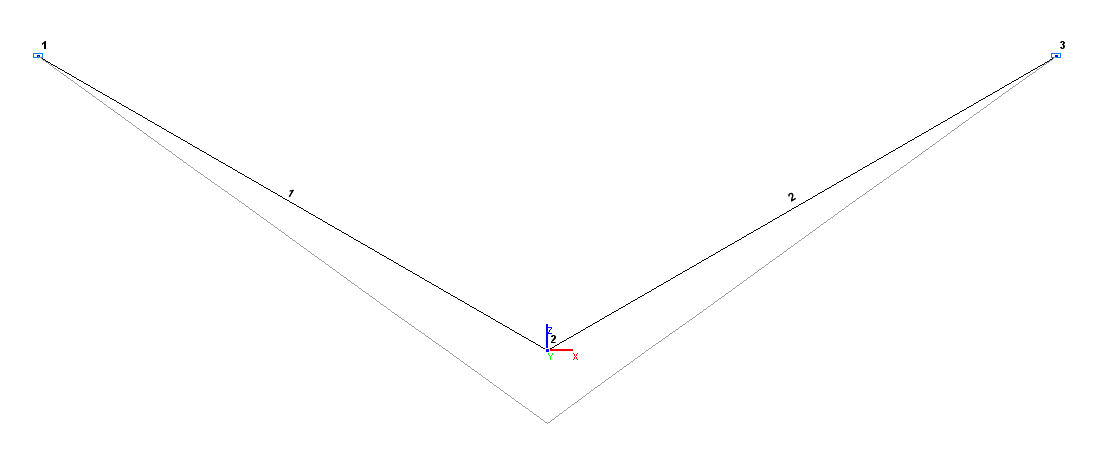
Расчетная и деформированная схемы

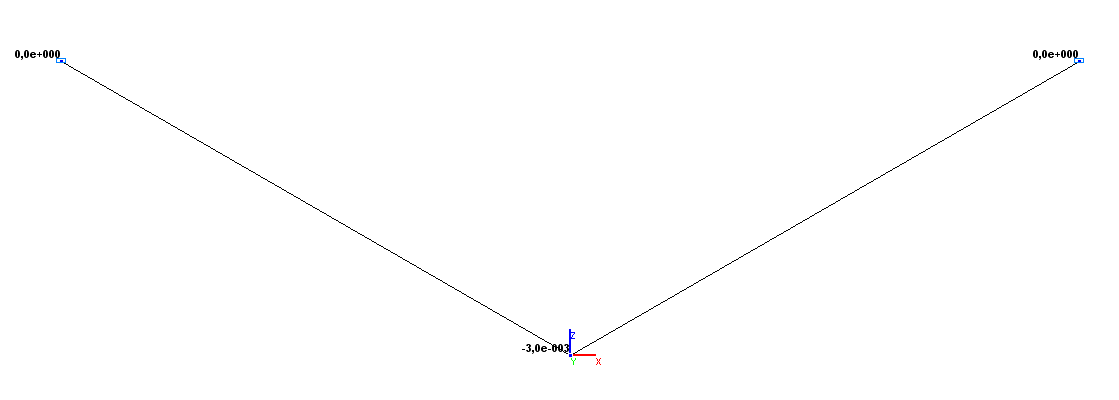
Значения вертикальных перемещений Z (м)

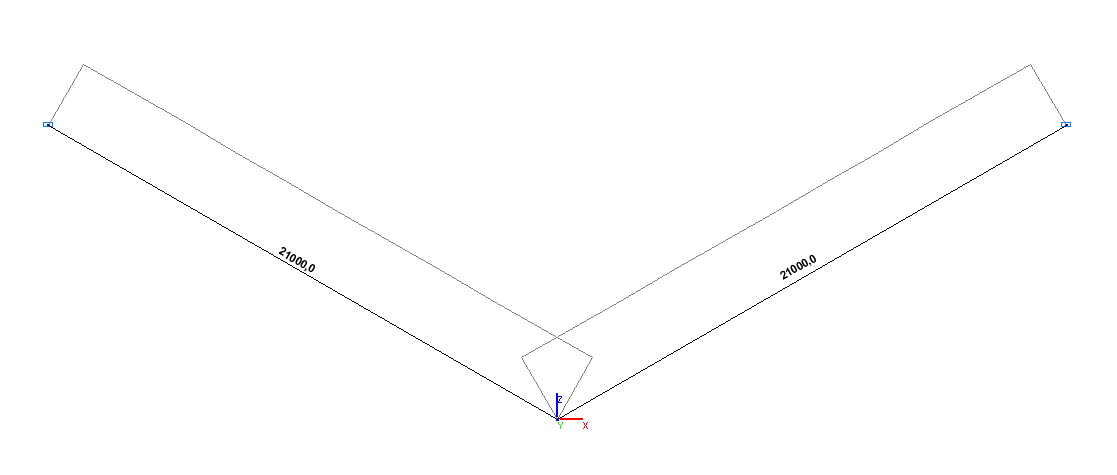
Значения продольных сил N (Н)

 

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Вертикальное перемещение Z (точка C), м	-3.0000·10-3	-3.0000·10-3	0.00
Продольная сила N (стержень AC), Н	21000.0	21000.0	0.00
Продольная сила N (стержень BC), Н	21000.0	21000.0	0.00

Замечания: При аналитическом решении вертикальное перемещение общего узла стержней фермы Z и продольные силы в стержнях фермы N определяются по следующим формулам:

\[ Z=\frac{F\cdot L}{2\cdot E\cdot A\cdot \sin^{2}\left( \theta \right)}; \]

\[ N=\frac{F}{2\cdot \sin \left( \theta \right)}. \]