Круговая тоннельная обделка под действием заданного активного вертикального и горизонтального давления грунта и пассивного давления упругого отпора грунта в зоне контакта

Цель: Определение внутренних усилий в конструкции круговой тоннельной обделки и упругих реакций грунта в зоне контакта от действия заданного вертикального и горизонтального давления грунта в конструктивно нелинейной постановке.

Файл с исходными данными: Tunnel_lining.spr

Формулировка задачи: Круговая тоннельная обделка подвергается воздействию заданного активного вертикального p и горизонтального q давления грунта от сводообразования и пассивного давления упругого отпора грунта в зоне контакта. Определить внутренние усилия (продольные силы N и изгибающие моменты M) в конструкции круговой тоннельной обделки и упругие реакции грунта R в зоне контакта.

Ссылки: М.М. Архангельский, Д.И. Джинчарадзе, А.С. Курисько, Расчет тоннельных обделок, Москва, ТРАНСЖЕЛДОРИЗДАТ, 1960, стр. 217

Исходные данные:

E = 3.4·10⁶ т/м²	- модуль упругости материала тоннельной обделки;
γ_b = 2.6 т/м³	- объемный вес материала тоннельной обделки;
dint = 7.1 м	- внутренний диаметр кольца тоннельной обделки;
h = 0.4	- толщина прямоугольного поперечного сечения тоннельной обделки;
b = 1.0	- ширина прямоугольного поперечного сечения тоннельной обделки;
α = π/8 рад	- центральный угол стороны правильного многоугольника рамы, заменяющей окружность расчетного радиуса r тоннельной обделки;
k = 5.0·10³ т/м³	- коэффициент упругого отпора грунта в зоне контакта с тоннельной обделкой;
f = 0.8	- коэффициент крепости грунта по Протодьяконову;
φ = 2·π/9 рад	- угол внутреннего трения грунта;
γ_g = 1.9 т/м³	- объемный вес грунта.
d_ext = d_int + 2·h = 7.9 м	- наружный диаметр кольца тоннельной обделки;
r = (d_ext + d_int)/4 = 3.75 м	- расчетный радиус тоннельной обделки;
S = 2·r·sin(0.5·α) = 1.463177 м	- сторона правильного многоугольника заменяющей рамы;
I = b·h³/12 = 0.005333 м⁴	- момент инерции поперечного сечения тоннельной обделки;
F = b·h = 0.4 м²	- площадь поперечного сечения тоннельной обделки;
D = k·S·b = 7315.887 т/м	- жесткость, радиально расположенных у вершин многоугольника заменяющей рамы упругих опор, моделирующих отпор грунта;
L_arch = d_ext·(1+ tg(π/4 – φ/2)) = 11.584 м	- пролет свода давления грунта;
H_arch = L_arch/(2·f) = 7.240 м	- высота свода давления грунта над шелыгой выработки;
p = H_arch·γ_g + h· γ_b =14.796 т/м²	- интенсивность вертикального равномерно распределенного активного давления грунта;
q = (H_arch + d_ext/2)· γg·tg²(π/4 – φ/2) = 4.623 т/м²	- интенсивность горизонтального равномерно распределенного активного давления грунта.

Вертикальные сосредоточенные силы в узлах многоугольника рамы, заменяющие распределенную нагрузку

P₁ = (S/2)∙p∙(cos(– 0.5∙α) + cos(0.5∙α)) = 21.2329 т;

P₂ = (S/2)∙p∙(cos(0.5∙α) + cos(1.5∙α)) = 19.6166 т;

P₃ = (S/2)∙p∙(cos(1.5∙α) + cos(2.5∙α)) = 15.0139 т;

P₄ = (S/2)∙p∙(cos(2.5∙α) + cos(3.5∙α)) = 8.1255 т;

P₅ = (S/2)∙p∙cos(3.5∙α) = 2.1117 т.

Горизонтальные сосредоточенные силы в узлах многоугольника рамы, заменяющие распределенную нагрузку

Q₁ = (S/2)∙q∙sin(0.5∙α) = 0.6598 т;

Q₂ = (S/2)∙q∙(sin(0.5∙α) + sin(1.5∙α)) = 2.5388 т;

Q₃ = (S/2)∙q∙(sin(1.5∙α) + sin(2.5∙α)) = 4.6911 т;

Q₄ = (S/2)∙q∙sin(2.5∙α) =2.8121 т.

Конечноэлементная модель: Расчетная схема – система общего вида. Элементы тоннельной обделки – 16 стержневых элементов типа 5. Сетка конечных элементов разбита по окружности радиуса r = 3.75 м, расположенной в плоскости XOZ общей системы координат, с шагом центрального угла α = π/8 рад. Начало общей системы координат находится в центре окружности. Оси X₁ местных систем координат элементов направлены по хордам окружности в направлении обхода по часовой стрелке вокруг оси Y общей системы координат, если смотреть от начала координат. Оси Z₁ местных систем координат элементов направлены от центра окружности. Элементы, моделирующие упругий отпор грунта – 16 элементов односторонних двухузловых связей, работающих на сжатие, типа 352. Конечные элементы сориентированы по радиусам окружности от центра и примыкают к узлам сопряжения элементов тоннельной обделки. Обеспечение граничных условий достигается за счет наложения связей на опорные узлы элементов упругого отпора грунта по направлениям степеней свободы X, Y, Z, а также на узлы элементов тоннельной обделки по направлению степени свободы Y. Для обеспечения геометрической неизменяемости системы на узлы элементов тоннельной обделки, расположенные по вертикальной оси симметрии, вводятся связи по направлению степени свободы X. Воздействие активного вертикального и горизонтального давления грунта задается в виде вертикальных P_i и горизонтальных Q_i сосредоточенных сил в узлах сопряжения элементов тоннельной обделки. Нелинейное загружение формировалось простым шаговым методом с коэффициентом загружения – 0.01 и количеством шагов - 100 для линейного загружения. Количество узлов в расчетной схеме – 32.

Результаты решения в SCAD

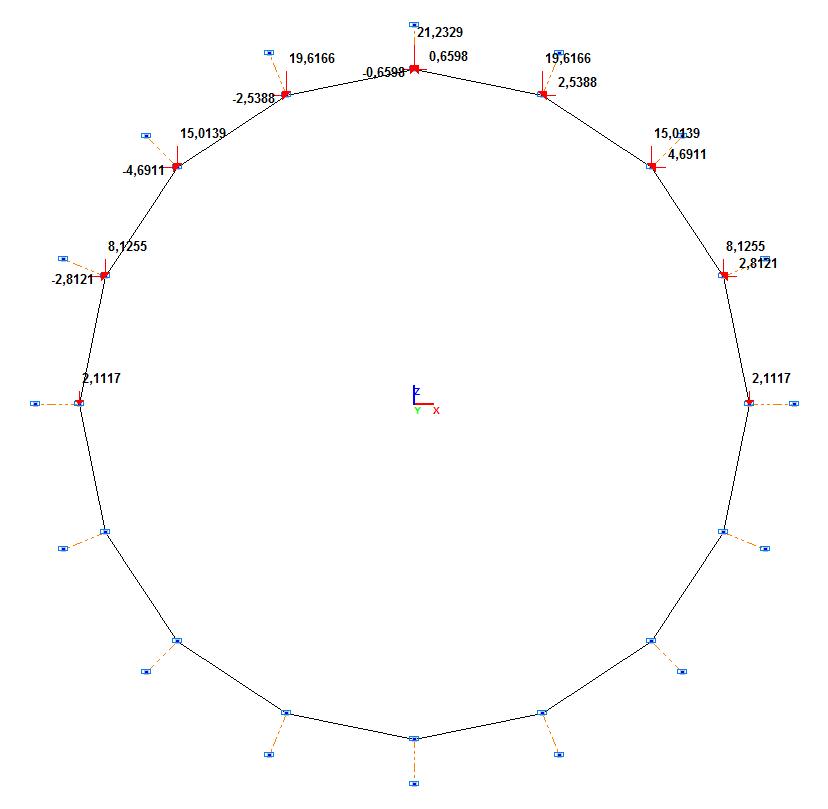
Расчетная схема

Деформированная схема

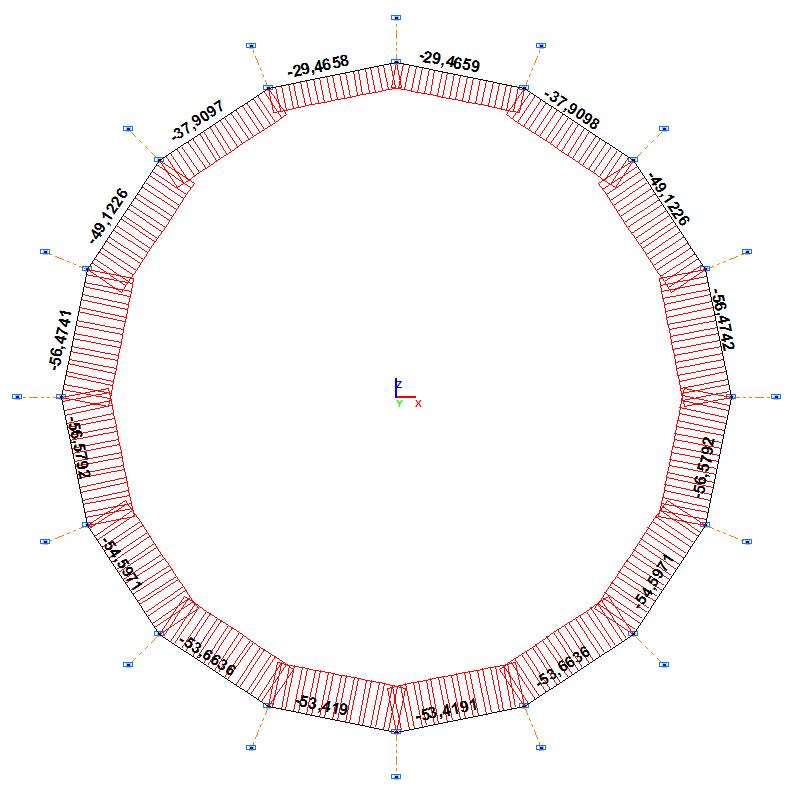
Эпюра продольных сил N, т

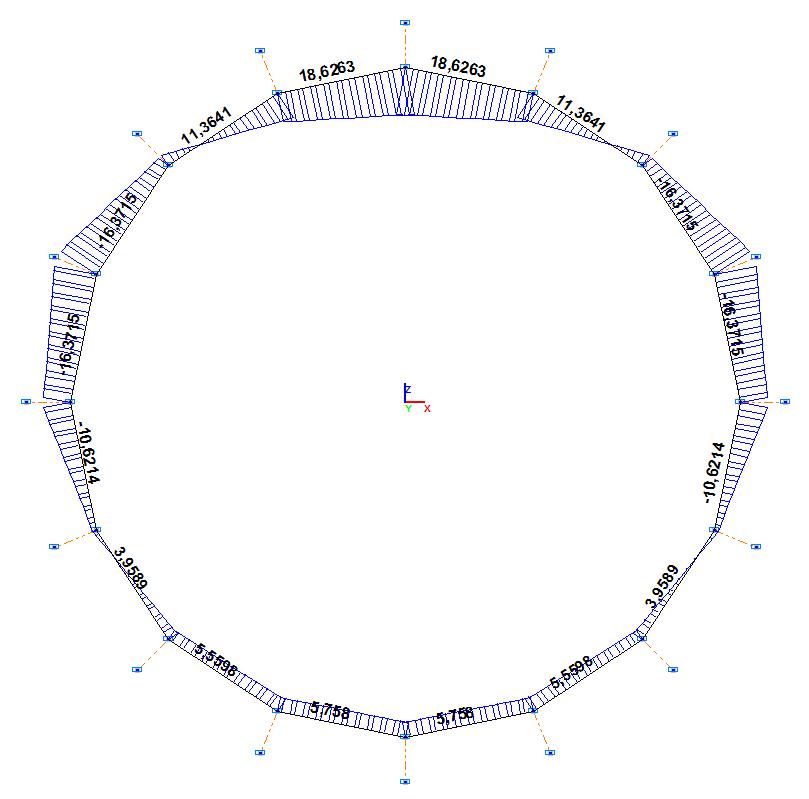
Эпюра изгибающих моментов M, т∙м

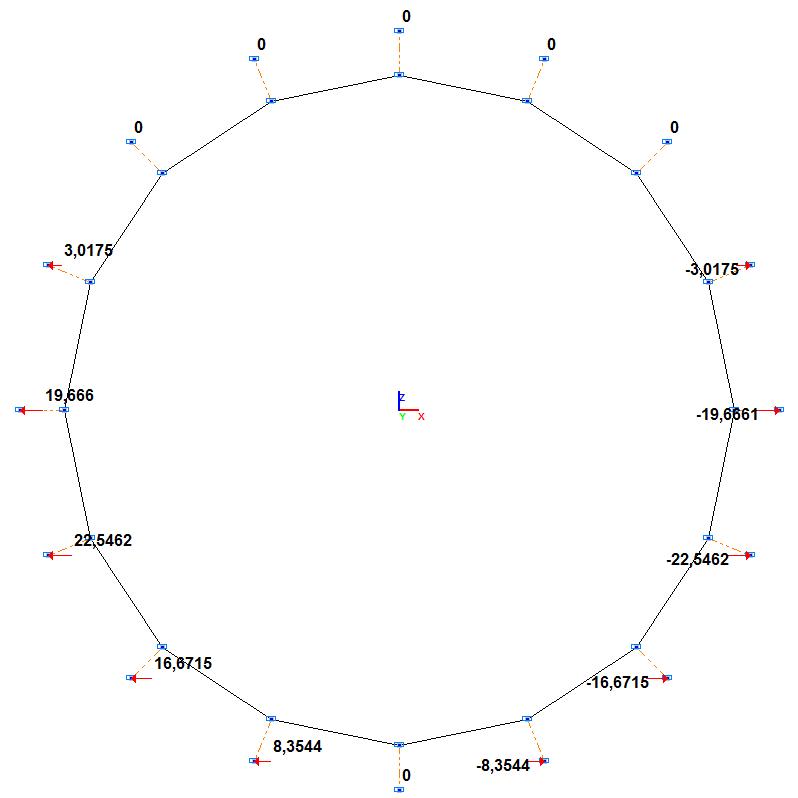
Значения реакций в опорных узлах вдоль оси X общей системы координат R_x, т

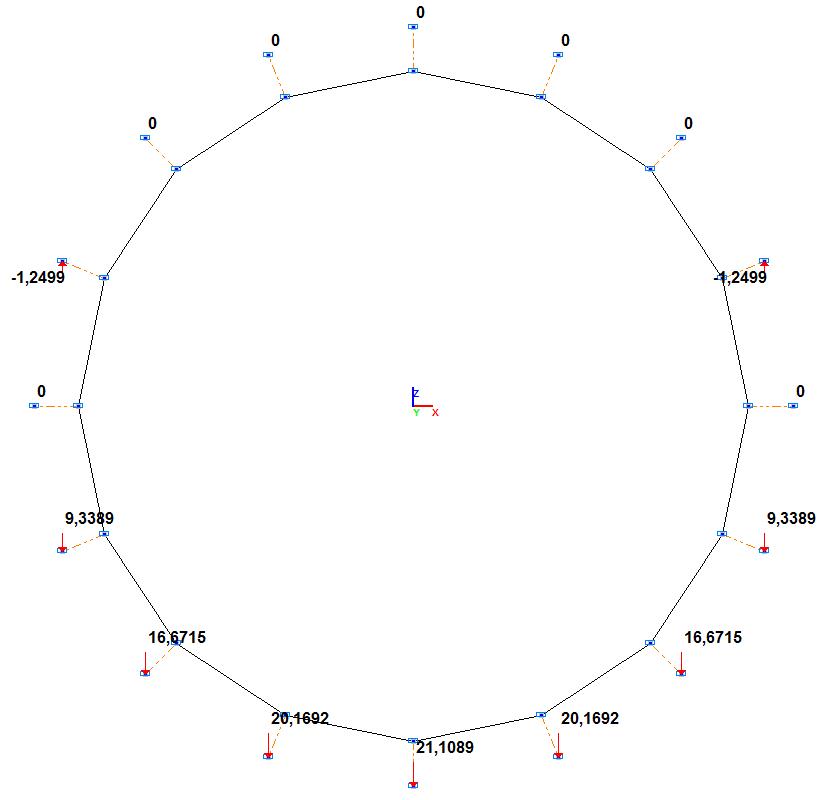
Значения реакций в опорных узлах вдоль оси Z общей системы координат R_z, т

Сравнение решений:

Параметр	Теория	SCAD	Отклонение, %
N₁₂, т	-29.4660	-29.4659	0.00
N₂₃, т	-37.9098	-37.9098	0.00
N₃₄, т	-49.1226	-49.1226	0.00
N₄₅, т	-56.4742	-56.4742	0.00
N₅₆, т	-56.5793	-56.5792	0.00
N₆₇, т	-54.5971	-54.5971	0.00
N₇₈, т	-53.6637	-53.6636	0.00
N₈₉, т	-53.4191	-53.4191	0.00
M₁, т•м	18.6263	18.6263	0.00
M₂, т•м	11.3641	11.3641	0.00
M₃, т•м	-4.7755	-4.7755	0.00
M₄, т•м	-16.3715	-16.3715	0.00
M₅, т•м	-10.6215	-10.6214	0.00
M₆, т•м	-1.3066	-1.3065	0.01
M₇, т•м	3.9589	3.9589	0.00
M₈, т•м	5.5598	5.5598	0.00
M₉, т•м	5.7581	5.7580	0.00
R₁, т	0.0000	0.0000	0.00
R₂, т	0.0000	0.0000	0.00
R₃, т	0.0000	0.0000	0.00
R₄, т	-3.2661	-3.0175•cos(π/8) - 1.2499•sin(π/8) = -3.2661	0.00
R₅, т	-19.6660	-19.6661	0.00
R₆, т	-24.4038	-22.5462•cos(π/8) - 9.3389•sin(π/8) = -24.4038	0.00
R₇, т	-23.5771	-16.6715•cos(π/4) – 16.6715•sin(π/4) = -23.5770	0.00
R₈, т	-21.8310	-8.3544•cos(3•π/8) - 20.1692•sin(3•π/8) = -21.8310	0.00
R₉, т	-21.1089	-21.1089	0.00

Замечания: В аналитическом решении применяется метод расчета тоннельных обделок, предложенный Метропроектом, в котором учитывается зависимость напряженного состояния конструкции от упругих свойств среды. Порядок расчета следующий:

Предварительно задается зона контакта конструкции с грунтом; окружность контура обделки заменяется правильным многоугольником; вычисляются все приведенные к узловым активные нагрузки и необходимые геометрические характеристики.
Принимается основная система метода сил в виде многоугольника с шарнирами во всех углах где имеются упругие опоры, а также в центральном угле зоны отлипания, благодаря чему верхняя часть многоугольника превращается в трехшарнирную арку; за неизвестные принимаются моменты, которые необходимо приложить в шарнирах, чтобы устранить возможность относительного поворота сторон многоугольника; прикладываются единичные моменты во всех шарнирах (для симметричной системы рассматривается действие парных неизвестных, действующих в симметричных узлах); последовательно вырезая узлы и проектируя силы на направления стержней, а также на биссектрису угла, находятся усилия в элементах шарнирной цепи и реакции упругих опор во всех единичных состояниях.
Верхняя часть многоугольника в зоне отлипания рассматривается как трехшарнирная арка, и определяются ее опорные вертикальные и горизонтальные давления от внешней нагрузки на остальную часть шарнирного многоугольника; под действием опорных сил, а также непосредственно приложенных в остальных узлах активных нагрузок путем последовательного вырезания узлов находятся усилия для всех элементов шарнирной цепи и реакции упругих опор.
Определяются единичные и грузовые перемещения по формулам Максвелла-Мора, прибегая к способам приближенного суммирования.
Для определения лишних неизвестных составляется и решается при помощи алгоритма Гаусса система канонических уравнений;
Находятся продольные силы, изгибающие моменты и реакции упругих опор.
По значениям реакций упругих опор проверяется правильность задания зоны контакта конструкции с грунтом.

Ниже приводятся формулы последовательности расчета.

Основная система метода сил

Определение усилий в основной системе от внешних нагрузок

Определение усилий в трехшарнирной арке от вертикальных нагрузок

Расчетная схема определения усилий в трехшарнирной арке от вертикальных нагрузок

\[ {\begin{array}{*{20}c} {L_{1} =r\cdot \sin \left( {3\cdot \alpha } \right)} & {L_{2} =r\cdot \sin \left( \alpha \right)} & {L_{3} =r\cdot \sin \left( {2\cdot \alpha } \right)} \\ {F_{1} =r\cdot \left( {1-\cos \left( {3\cdot \alpha } \right)} \right)} & {F_{2} =r\cdot \left( {\cos \left( \alpha \right)-\cos \left( {3\cdot \alpha } \right)} \right)} & {F_{3} =r\cdot \left( {\cos \left( {2\cdot \alpha } \right)-\cos \left( {3\cdot \alpha } \right)} \right)} \\ \end{array} } \] \[ V=0.5\cdot P_{1} +P_{2} +P_{3} \quad H=\frac{V\cdot L_{1} -P_{2} \cdot L_{2} -P_{3} \cdot L_{3} }{F_{1} } \] \[ M_{3p} =V\cdot \left( {L_{1} -L_{3} } \right)-H\cdot F_{3} \quad M_{2p} =V\cdot \left( {L_{1} -L_{3} } \right)-H\cdot F_{2} -P_{3} \cdot \left( {L_{3} -L_{2} } \right) \] \[ N_{12p} =H\cdot \cos \left( {0.5\cdot \alpha } \right)+\frac{P_{1} }{2}\cdot \sin \left( {0.5\cdot \alpha } \right) \quad N_{23p} =H\cdot \cos \left( {1.5\cdot \alpha } \right)+\left( {\frac{P_{1} }{2}+P_{2} } \right)\cdot \sin \left( {1.5\cdot \alpha } \right) \] \[ N_{34p} =H\cdot \cos \left( {2.5\cdot \alpha } \right)+\left( {\frac{P_{1} }{2}+P_{2} +P_{3} } \right)\cdot \sin \left( {2.5\cdot \alpha } \right) \]

Определение усилий в шарнирной цепи от вертикальных нагрузок

Расчетная схема определения усилий шарнирной цепи от вертикальных нагрузок

\[ N_{45p} =\frac{\left( {V+P_{4} } \right)\cdot \sin \left( {3\cdot \alpha } \right)+H\cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}; \quad N_{56p} =N_{45p} +\frac{P_{5} }{\cos \left( {0.5\cdot \alpha } \right)}; \] \[ N_{67p} =N_{78p} =N_{89p} =N_{56p} ; \] \[ R_{4p} =H\cdot \cos \left( \alpha \right)+N_{45p} \cdot \sin \left( {0.5\cdot \alpha } \right)-\left( {V+P_{4} } \right)\cdot \cos \left( {3\cdot \alpha } \right); \] \[ R_{5p} =\left( {N_{45p} +N_{56p} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{6p} =\left( {N_{56p} +N_{67p} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{7p} =R_{8p} =R_{9p} =R_{6p} . \] \[ \text {Определение усилий в трехшарнирной арке от горизонтальных нагрузок}\] \[ H_{cr} =\frac{Q_{1} \cdot F_{1} +Q_{2} \cdot F_{2} +Q_{3} \cdot F_{3} }{F_{1} }\quad ; \quad H_{sk} =\frac{Q_{2} \cdot \left( {F_{1} -F_{2} } \right)+Q_{3} \cdot \left( {F_{1} -F_{3} } \right)}{F_{1} }; \] \[ M_{2q} =\left( {H_{cr} -Q_{1} } \right)\cdot \left( {F_{1} -F_{2} } \right); \quad M_{3q} =H_{sk} \cdot F_{3} ; \] \[ N_{12q} =\left( {H_{cr} -Q_{1} } \right)\cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{23q} =\left( {H_{cr} -Q_{1} -Q_{2} } \right)\cdot \cos \left( {1.5\cdot \alpha } \right); \] \[ N_{34q} =-H_{sk} \cdot \cos \left( {2.5\cdot \alpha } \right). \] \[ \text {Определение усилий в шарнирной цепи от горизонтальных нагрузок} \] \[ N_{45q} =-\frac{\left( {H_{sk} +Q_{4} } \right)\cdot \cos \left( {3\cdot \alpha } \right)}{\cos \left( {0.5\cdot \alpha } \right)}\quad ; \quad N_{56q} =N_{67q} =N_{78q} =N_{89q} =N_{45q} ; \] \[ R_{4q} =-\left( {H_{sk} +Q_{4} } \right)\cdot \sin \left( {3\cdot \alpha } \right)+N_{45q} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{5q} =\left( {N_{45q} +N_{56q} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{6q} =R_{7q} =R_{8q} =R_{9q} =R_{5q} . \] \[ \text {Определение усилий в основной системе от единичных моментов} \] \[ \text {Определение усилий в трехшарнирной арке от единичного момента, приложенного в точке 1 }\] \[ M_{11} =1\quad ; \quad H_{1} =\frac{M_{11} }{F_{1} }; \] \[ M_{21} =H_{1} \cdot F_{2} ; \quad M_{31} =H_{1} \cdot F_{3} ; \] \[ N_{121} =-H_{1} \cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{231} =-H_{1} \cdot \cos \left( {1.5\cdot \alpha } \right); \quad N_{341} =-H_{1} \cdot \cos \left( {2.5\cdot \alpha } \right). \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 1}\] \[ N_{451} =-\frac{H_{1} \cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}; \quad N_{561} =N_{671} =N_{781} =N_{891} =N_{451} ; \] \[ R_{41} =N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right)-H_{1} \cdot \cos \left( \alpha \right); \quad R_{51} =2\cdot N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{61} =R_{71} =R_{81} =R_{91} =R_{51} . \] \[ \text {Определение усилий в трехшарнирной арке от единичного момента, приложенного в точке 4}\] \[ M_{44} =1\quad ; \quad H_{4} =\frac{M_{44} }{F_{1} }; \] \[ M_{24} =M_{44} -H_{4} \cdot F_{2} ; \quad M_{34} =M_{44} -H_{4} \cdot F_{3} ; \] \[ N_{124} =H_{4} \cdot \cos \left( {0.5\cdot \alpha } \right); \quad N_{234} =H_{4} \cdot \cos \left( {1.5\cdot \alpha } \right); \quad N_{344} =H_{4} \cdot \cos \left( {2.5\cdot \alpha } \right). \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 4 }\] \[ N_{454} =\frac{H_{4} \cdot \sin \left( \alpha \right)}{\cos \left( {0.5\cdot \alpha } \right)}+\frac{M_{44} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{564} =N_{454} +\frac{M_{44} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \] \[ N_{674} =N_{784} =N_{894} =N_{564} ; \] \[ R_{41} =N_{451} \cdot \sin \left( {0.5\cdot \alpha } \right)+H_{4} \cdot \cos \left( \alpha \right)+\frac{M_{44} \cdot \cos \left( \alpha \right)}{S}; R_{51} =-\frac{M_{44} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+\left( {N_{454} +N_{564} } \right)\cdot \sin \left( {0.5\cdot \alpha } \right); \] \[ R_{64} =2\cdot N_{564} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{74} =R_{84} =R_{94} =R_{64} . \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 5 }\] \[ M_{55} =1; \] \[ N_{455} =-\frac{M_{55} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{565} =N_{455} ; \] \[ R_{45} =-\frac{M_{55} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{55} =\frac{2\cdot M_{55} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{455} \cdot \sin \left( {0.5\cdot \alpha } \right); R_{65} =-\frac{M_{55} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 6 }\] \[ M_{66} =1; \] \[ N_{566} =-\frac{M_{66} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{676} =N_{566} ; \] \[ R_{56} =-\frac{M_{66} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{66} =\frac{2\cdot M_{66} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{566} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{76} =-\frac{M_{66} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 7 } \] \[ M_{77} =1; \] \[ N_{677} =-\frac{M_{77} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{787} =N_{677} ; \] \[ R_{67} =-\frac{M_{77} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{77} =\frac{2\cdot M_{77} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{677} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{87} =-\frac{M_{77} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 8 } \] \[ M_{88} =1; \] \[ N_{788} =-\frac{M_{88} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad N_{898} =N_{788} ; \] \[ R_{78} =-\frac{M_{88} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{88} =\frac{2\cdot M_{88} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{788} \cdot \sin \left( {0.5\cdot \alpha } \right); \quad R_{98} =-\frac{2\cdot M_{88} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}. \] \[ \text {Определение усилий в шарнирной цепи от единичного момента, приложенного в точке 9 }\] \[ M_{99} =1; \] \[ N_{899} =-\frac{M_{99} \cdot \sin \left( {0.5\cdot \alpha } \right)}{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \] \[ R_{89} =-\frac{M_{99} }{S\cdot \cos \left( {0.5\cdot \alpha } \right)}; \quad R_{99} =\frac{2\cdot M_{99} \cdot \cos \left( {0.5\cdot \alpha } \right)}{S}+2\cdot N_{899} \cdot \sin \left( {0.5\cdot \alpha } \right). \] \[ \text {Определение перемещений} \] \[ \delta_{11R} =2\cdot \frac{1}{D}\cdot \left( {R_{41}^{2}+R_{51} ^{2}+R_{61}^{2}+R_{71}^{2}+R_{81}^{2}+R_{91}^{2}\cdot 0.5} \right); \] \[ \delta_{11M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot \left( {M_{11} ^{2}+M_{11} \cdot M_{21} +2\cdot M_{21}^{2}+M_{21} \cdot M_{31} +2\cdot M_{31}^{2}} \right); \] \[ \delta_{11N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{121}^{2}+N_{231} ^{2}+N_{341}^{2}+N_{451}^{2}+N_{561}^{2}+N_{671}^{2}+N_{781} ^{2}+N_{891}^{2}} \right); \] \[ \delta_{11} =\delta_{11R} +\delta_{11M} +\delta_{11N} ; \] \[ \delta_{14R} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{44} +R_{51} \cdot R_{54} +R_{61} \cdot R_{64} +R_{71} \cdot R_{74} +R_{81} \cdot R_{84} +R_{91} \cdot R_{94} \cdot 0.5} \right); \] \[ \delta_{14M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {M_{11} \cdot M_{24} +4\cdot M_{21} \cdot M_{24} +M_{21} \cdot M_{34} +M_{31} \cdot M_{24} +4\cdot M_{31} \cdot M_{34} +M_{31} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{14N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{121} \cdot N_{124} +N_{231} \cdot N_{234} +N_{341} \cdot N_{344} +N_{451} \cdot N_{454} +} \right.} \\ {\left. {N_{561} \cdot N_{564} +N_{671} \cdot N_{674} +N_{781} \cdot N_{784} +N_{891} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{14} =\delta_{14R} +\delta_{14M} +\delta_{14N} ; \] \[ \delta_{15R} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{45} +R_{51} \cdot R_{55} +R_{61} \cdot R_{65} } \right); \quad \delta_{15M} =0; \] \[ \delta_{15N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{451} \cdot N_{455} +N_{561} \cdot N_{565} } \right); \quad \delta_{15} =\delta_{15R} +\delta_{15M} +\delta_{15N} ; \] \[ \delta_{16R} =2\cdot \frac{1}{D}\cdot \left( {R_{51} \cdot R_{56} +R_{61} \cdot R_{66} +R_{71} \cdot R_{76} } \right); \quad \delta_{16M} =0; \] \[ \delta_{16N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{561} \cdot N_{566} +N_{671} \cdot N_{676} } \right); \quad \delta_{16} =\delta_{16R} +\delta_{16M} +\delta_{16N} ; \] \[ \delta_{17R} =2\cdot \frac{1}{D}\cdot \left( {R_{61} \cdot R_{67} +R_{71} \cdot R_{77} +R_{81} \cdot R_{87} } \right); \quad \delta_{17M} =0; \] \[ \delta_{17N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{671} \cdot N_{677} +N_{781} \cdot N_{787} } \right); \quad \delta_{17} =\delta_{17R} +\delta_{17M} +\delta_{17N} ; \] \[ \delta_{18R} =2\cdot \frac{1}{D}\cdot \left( {R_{71} \cdot R_{78} +R_{81} \cdot R_{88} +R_{91} \cdot R_{98} \cdot 0.5} \right); \quad \delta_{18M} =0; \] \[ \delta_{18N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{781} \cdot N_{788} +N_{891} \cdot N_{898} } \right); \quad \delta_{18} =\delta_{18R} +\delta_{18M} +\delta_{18N} ; \] \[ \delta_{19R} =2\cdot \frac{1}{D}\cdot \left( {R_{81} \cdot R_{89} +R_{91} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{19M} =0; \quad \delta_{19N} =2\cdot \frac{S}{E\cdot F}\cdot N_{891} \cdot N_{899} ; \] \[ \delta_{19} =\delta_{19R} +\delta_{19M} +\delta_{19N} ; \] \[ \delta_{44R} =2\cdot \frac{1}{D}\cdot \left( {R_{44}^{2}+R_{54} ^{2}+R_{64}^{2}+R_{74}^{2}+R_{84}^{2}+R_{94}^{2}\cdot 0.5} \right); \] \[ \delta_{44M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot \left( {2\cdot M_{24} ^{2}+2\cdot M_{34}^{2}+M_{24} \cdot M_{34} +2\cdot M_{44}^{2}+M_{34} \cdot M_{44} } \right); \] \[ \delta_{44N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{124}^{2}+N_{234} ^{2}+N_{344}^{2}+N_{454}^{2}+N_{564}^{2}+N_{674}^{2}+N_{784} ^{2}+N_{894}^{2}} \right); \] \[ \delta_{44} =\delta_{44R} +\delta_{44M} +\delta_{44N} ; \] \[ \delta_{45R} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{45} +R_{54} \cdot R_{55} +R_{64} \cdot R_{65} } \right); \quad \delta_{45M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{44} \cdot M_{55} ; \] \[ \delta_{45N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{454} \cdot N_{455} +N_{564} \cdot N_{565} } \right); \] \[ \delta_{45} =\delta_{45R} +\delta_{45M} +\delta_{45N} ; \] \[ \delta_{46R} =2\cdot \frac{1}{D}\cdot \left( {R_{54} \cdot R_{56} +R_{64} \cdot R_{66} +R_{74} \cdot R_{76} } \right); \quad \delta_{46M} =0; \quad \delta_{46N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{564} \cdot N_{566} +N_{674} \cdot N_{676} } \right); \] \[ \delta_{46} =\delta_{46R} +\delta_{46M} +\delta_{46N} ; \] \[ \delta_{47R} =2\cdot \frac{1}{D}\cdot \left( {R_{64} \cdot R_{67} +R_{74} \cdot R_{77} +R_{84} \cdot R_{87} } \right); \quad \delta_{47M} =0; \quad \delta_{47N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{674} \cdot N_{677} +N_{784} \cdot N_{787} } \right); \] \[ \delta_{47} =\delta_{47R} +\delta_{47M} +\delta_{47N} ; \] \[ \delta_{48R} =2\cdot \frac{1}{D}\cdot \left( {R_{74} \cdot R_{78} +R_{84} \cdot R_{88} +R_{94} \cdot R_{98} \cdot 0.5} \right); \quad \delta_{48M} =0; \quad \delta_{48N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{784} \cdot N_{788} +N_{894} \cdot N_{898} } \right); \] \[ \delta_{48} =\delta_{48R} +\delta_{48M} +\delta_{48N} ; \] \[ \delta_{49R} =2\cdot \frac{1}{D}\cdot \left( {R_{84} \cdot R_{89} +R_{94} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{49M} =0; \quad \delta_{49N} =2\cdot \frac{S}{E\cdot F}\cdot N_{894} \cdot N_{899} ; \] \[ \delta_{49} =\delta_{49R} +\delta_{49M} +\delta_{49N} ; \] \[ \delta_{55R} =2\cdot \frac{1}{D}\cdot \left( {R_{45}^{2}+R_{55} ^{2}+R_{65}^{2}} \right); \quad \delta_{55M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{55}^{2}; \quad \delta_{55N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{455}^{2}+N_{565} ^{2}} \right); \] \[ \delta_{55} =\delta_{55R} +\delta_{55M} +\delta_{55N} ; \] \[ \delta_{56R} =2\cdot \frac{1}{D}\cdot \left( {R_{55} \cdot R_{56} +R_{65} \cdot R_{66} } \right); \quad \delta_{56M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{55} \cdot M_{66} ; \quad \delta_{56N} =2\cdot \frac{S}{E\cdot F}\cdot N_{565} \cdot N_{566} ; \] \[ \delta_{56} =\delta_{56R} +\delta_{56M} +\delta_{56N} ; \] \[ \delta_{57R} =2\cdot \frac{1}{D}\cdot R_{65} \cdot R_{67} ; \quad \delta_{57M} =0; \quad \delta_{57N} =0; \] \[ \delta_{57} =\delta_{57R} +\delta_{57M} +\delta_{57N} ; \] \[ \delta_{58R} =0; \quad \delta_{58M} =0; \quad \delta_{58N} =0; \] \[ \delta_{58} =\delta_{58R} +\delta_{58M} +\delta_{58N} ; \] \[ \delta_{59R} =0; \quad \delta_{59M} =0; \quad \delta_{59N} =0; \] \[ \delta_{59} =\delta_{59R} +\delta_{59M} +\delta_{59N} ; \] \[ \delta_{66R} =2\cdot \frac{1}{D}\cdot \left( {R_{56}^{2}+R_{66} ^{2}+R_{76}^{2}} \right); \quad \delta_{66M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{66}^{2}; \quad \delta_{66N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{566}^{2}+N_{676} ^{2}} \right); \] \[ \delta_{66} =\delta_{66R} +\delta_{66M} +\delta_{66N} ; \] \[ \delta_{67R} =2\cdot \frac{1}{D}\cdot \left( {R_{66} \cdot R_{67} +R_{76} \cdot R_{77} } \right); \quad \delta_{67M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{66} \cdot M_{77} ; \quad \delta_{67N} =2\cdot \frac{S}{E\cdot F}\cdot N_{676} \cdot N_{677} ; \] \[ \delta_{67} =\delta_{67R} +\delta_{67M} +\delta_{67N} ; \] \[ \delta_{68R} =2\cdot \frac{1}{D}\cdot R_{76} \cdot R_{78} ; \quad \delta_{68M} =0; \quad \delta_{68N} =0; \] \[ \delta_{68} =\delta_{68R} +\delta_{68M} +\delta_{68N} ; \] \[ \delta_{69R} =0; \quad \delta_{69M} =0; \quad \delta_{69N} =0; \] \[ \delta_{69} =\delta_{69R} +\delta_{69M} +\delta_{69N} ; \] \[ \delta_{77R} =2\cdot \frac{1}{D}\cdot \left( {R_{67}^{2}+R_{77} ^{2}+R_{87}^{2}} \right); \quad \delta_{77M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{77}^{2}; \quad \delta_{77N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{677}^{2}+N_{787} ^{2}} \right); \] \[ \delta_{77} =\delta_{77R} +\delta_{77M} +\delta_{77N} ; \] \[ \delta_{78R} =2\cdot \frac{1}{D}\cdot \left( {R_{77} \cdot R_{78} +R_{87} \cdot R_{88} } \right); \quad \delta_{78M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{77} \cdot M_{88} ; \quad \delta_{78N} =2\cdot \frac{S}{E\cdot F}\cdot N_{787} \cdot N_{788} ; \] \[ \delta_{78} =\delta_{78R} +\delta_{78M} +\delta_{78N} ; \] \[ \delta_{79R} =2\cdot \frac{1}{D}\cdot R_{87} \cdot R_{89} ; \quad \delta_{79M} =0; \quad \delta_{79N} =0; \] \[ \delta_{79} =\delta_{79R} +\delta_{79M} +\delta_{79N} ; \] \[ \delta_{88R} =2\cdot \frac{1}{D}\cdot \left( {R_{78}^{2}+R_{88} ^{2}+R_{98}^{2}\cdot 0.5} \right); \quad \delta_{88M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot 2\cdot M_{88}^{2}; \quad \delta_{88N} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{788}^{2}+N_{898} ^{2}} \right); \] \[ \delta_{88} =\delta_{88R} +\delta_{88M} +\delta_{88N} ; \] \[ \delta_{89R} =2\cdot \frac{1}{D}\cdot \left( {R_{88} \cdot R_{89} +R_{98} \cdot R_{99} \cdot 0.5} \right); \quad \delta_{89M} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot M_{88} \cdot M_{99} ; \quad \delta_{89N} =2\cdot \frac{S}{E\cdot F}\cdot N_{898} \cdot N_{899} ; \] \[ \delta_{89} =\delta_{89R} +\delta_{89M} +\delta_{89N} ; \] \[ \delta_{99R} =2\cdot \frac{1}{D}\cdot \left( {R_{89}^{2}+R_{99}^{2}\cdot 0.5} \right); \quad \delta_{99M} =2\cdot \frac{S}{3\cdot E\cdot I}\cdot M_{99}^{2}; \quad \delta_{99N} =2\cdot \frac{S}{E\cdot F}\cdot N_{899}^{2}; \] \[ \delta_{99} =\delta_{99R} +\delta_{99M} +\delta_{99N} ; \] \[ \delta_{1pR} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{4p} +R_{51} \cdot R_{5p} +R_{61} \cdot R_{6p} +R_{71} \cdot R_{7p} +R_{81} \cdot R_{8p} +R_{91} \cdot R_{9p} \cdot 0.5} \right); \] \[ \delta_{1pM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2p} \cdot M_{21} +M_{2p} \cdot M_{11} +4\cdot M_{3p} \cdot M_{31} +M_{3p} \cdot M_{21} +M_{2p} \cdot M_{31} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{1pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12p} \cdot N_{121} +N_{23p} \cdot N_{231} +N_{34p} \cdot N_{341} +N_{45p} \cdot N_{451} +} \right.} \\ {\left. {N_{56p} \cdot N_{561} +N_{67p} \cdot N_{671} +N_{78p} \cdot N_{781} +N_{89p} \cdot N_{891} } \right);} \\ \end{array} } \] \[ \delta_{1p} =\delta_{1pR} +\delta_{1pM} +\delta_{1pN} ; \] \[ \delta_{4pR} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{4p} +R_{54} \cdot R_{5p} +R_{64} \cdot R_{6p} +R_{74} \cdot R_{7p} +R_{84} \cdot R_{8p} +R_{94} \cdot R_{9p} \cdot 0.5} \right); \] \[ \delta_{4pM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2p} \cdot M_{24} +4\cdot M_{3p} \cdot M_{34} +M_{3p} \cdot M_{24} +M_{2p} \cdot M_{34} +M_{3p} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{4pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12p} \cdot N_{124} +N_{23p} \cdot N_{234} +N_{34p} \cdot N_{344} +N_{45p} \cdot N_{454} +} \right.} \\ {\left. {N_{56p} \cdot N_{564} +N_{67p} \cdot N_{674} +N_{78p} \cdot N_{784} +N_{89p} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{4p} =\delta_{4pR} +\delta_{4pM} +\delta_{4pN} ; \] \[ \delta_{5pR} =2\cdot \frac{1}{D}\cdot \left( {R_{45} \cdot R_{4p} +R_{55} \cdot R_{5p} +R_{65} \cdot R_{6p} } \right); \quad \delta_{5pM} =0; \quad \delta_{5pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{45p} \cdot N_{455} +N_{56p} \cdot N_{565} } \right); \] \[ \delta_{5p} =\delta_{5pR} +\delta_{5pM} +\delta_{5pN} ; \] \[ \delta_{6pR} =2\cdot \frac{1}{D}\cdot \left( {R_{56} \cdot R_{5p} +R_{66} \cdot R_{6p} +R_{76} \cdot R_{7p} } \right); \quad \delta_{6pM} =0; \quad \delta_{6pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{56p} \cdot N_{566} +N_{67p} \cdot N_{676} } \right); \] \[ \delta_{6p} =\delta_{6pR} +\delta_{6pM} +\delta_{6pN} ; \] \[ \delta_{7pR} =2\cdot \frac{1}{D}\cdot \left( {R_{67} \cdot R_{6p} +R_{77} \cdot R_{7p} +R_{87} \cdot R_{8p} } \right); \quad \delta_{7pM} =0; \quad \delta_{7pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{67p} \cdot N_{677} +N_{78p} \cdot N_{787} } \right); \] \[ \delta_{7p} =\delta_{7pR} +\delta_{7pM} +\delta_{7pN} ; \] \[ \delta_{8pR} =2\cdot \frac{1}{D}\cdot \left( {R_{78} \cdot R_{7p} +R_{88} \cdot R_{8p} +R_{98} \cdot R_{9p} \cdot 0.5} \right); \quad \delta_{8pM} =0; \quad \delta_{8pN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{78p} \cdot N_{788} +N_{89p} \cdot N_{898} } \right); \] \[ \delta_{8p} =\delta_{8pR} +\delta_{8pM} +\delta_{8pN} ; \] \[ \delta_{9pR} =2\cdot \frac{1}{D}\cdot \left( {R_{89} \cdot R_{8p} +R_{99} \cdot R_{9p} \cdot 0.5} \right); \quad \delta_{9pM} =0; \quad \delta_{9pN} =2\cdot \frac{S}{E\cdot F}\cdot N_{89p} \cdot N_{899} ; \] \[ \delta_{9p} =\delta_{9pR} +\delta_{9pM} +\delta_{9pN} ; \] \[ \delta_{1qR} =2\cdot \frac{1}{D}\cdot \left( {R_{41} \cdot R_{4q} +R_{51} \cdot R_{5q} +R_{61} \cdot R_{6q} +R_{71} \cdot R_{7q} +R_{81} \cdot R_{8q} +R_{91} \cdot R_{9q} \cdot 0.5} \right); \] \[ \delta_{1qM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{2q} \cdot M_{21} +M_{2q} \cdot M_{11} +4\cdot M_{3q} \cdot M_{31} +M_{3q} \cdot M_{21} +M_{2q} \cdot M_{31} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{1qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12q} \cdot N_{121} +N_{23q} \cdot N_{231} +N_{34q} \cdot N_{341} +N_{45q} \cdot N_{451} +} \right.} \\ {\left. {N_{56q} \cdot N_{561} +N_{67q} \cdot N_{671} +N_{78q} \cdot N_{781} +N_{89q} \cdot N_{891} } \right);} \\ \end{array} } \] \[ \delta_{1q} =\delta_{1qR} +\delta_{1qM} +\delta_{1qN} ; \] \[ \delta_{4qR} =2\cdot \frac{1}{D}\cdot \left( {R_{44} \cdot R_{4q} +R_{54} \cdot R_{5q} +R_{64} \cdot R_{6q} +R_{74} \cdot R_{7q} +R_{84} \cdot R_{8q} +R_{94} \cdot R_{9q} \cdot 0.5} \right); \] \[ \delta_{4qM} =2\cdot \frac{S}{6\cdot E\cdot I}\cdot \left( {4\cdot M_{qp} \cdot M_{24} +4\cdot M_{qp} \cdot M_{34} +M_{3q} \cdot M_{24} +M_{2q} \cdot M_{34} +M_{3q} \cdot M_{44} } \right); \] \[ {\begin{array}{*{20}c} {\delta_{4qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{12q} \cdot N_{124} +N_{23q} \cdot N_{234} +N_{34q} \cdot N_{344} +N_{45q} \cdot N_{454} +} \right.} \\ {\left. {N_{56q} \cdot N_{564} +N_{67q} \cdot N_{674} +N_{78q} \cdot N_{784} +N_{89q} \cdot N_{894} } \right);} \\ \end{array} } \] \[ \delta_{4q} =\delta_{4qR} +\delta_{4qM} +\delta_{4qN} ; \] \[ \delta_{5qR} =2\cdot \frac{1}{D}\cdot \left( {R_{45} \cdot R_{4q} +R_{55} \cdot R_{5q} +R_{65} \cdot R_{6q} } \right); \quad \delta_{5qM} =0; \quad \delta_{5qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{45q} \cdot N_{455} +N_{56q} \cdot N_{565} } \right); \] \[ \delta_{5q} =\delta_{5qR} +\delta_{5qM} +\delta_{5qN} ; \] \[ \delta_{6qR} =2\cdot \frac{1}{D}\cdot \left( {R_{56} \cdot R_{5q} +R_{66} \cdot R_{6q} +R_{76} \cdot R_{7q} } \right); \quad \delta_{6qM} =0; \quad \delta_{6qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{56q} \cdot N_{566} +N_{67q} \cdot N_{676} } \right); \] \[ \delta_{6q} =\delta_{6qR} +\delta_{6qM} +\delta_{6qN} ; \] \[ \delta_{7qR} =2\cdot \frac{1}{D}\cdot \left( {R_{67} \cdot R_{6q} +R_{77} \cdot R_{7q} +R_{87} \cdot R_{8q} } \right); \quad \delta_{7qM} =0; \quad \delta_{7qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{67q} \cdot N_{677} +N_{78q} \cdot N_{787} } \right); \] \[ \delta_{7q} =\delta_{7qR} +\delta_{7qM} +\delta_{7qN} ; \] \[ \delta_{8qR} =2\cdot \frac{1}{D}\cdot \left( {R_{78} \cdot R_{7q} +R_{88} \cdot R_{8q} +R_{98} \cdot R_{9q} \cdot 0.5} \right); \quad \delta_{8qM} =0; \quad \delta_{8qN} =2\cdot \frac{S}{E\cdot F}\cdot \left( {N_{78q} \cdot N_{788} +N_{89q} \cdot N_{898} } \right); \] \[ \delta_{8q} =\delta_{8qR} +\delta_{8qM} +\delta_{8qN} ; \] \[ \delta_{9qR} =2\cdot \frac{1}{D}\cdot \left( {R_{89} \cdot R_{8q} +R_{99} \cdot R_{9q} \cdot 0.5} \right); \quad \delta_{9qM} =0; \quad \delta_{9qN} =2\cdot \frac{S}{E\cdot F}\cdot N_{89q} \cdot N_{899} ; \] \[ \delta_{9q} =\delta_{9qR} +\delta_{9qM} +\delta_{9qN} . \] \[ \text {Определение лишних неизвестных } \] \[ \Delta_{1} =\left[ {{\begin{array}{*{20}c} {\delta_{11} } & {\delta_{14} } & {\delta_{15} } & {\delta_{16} } & {\delta_{17} } & {\delta_{18} } & {\delta_{19} } \\ {\delta_{14} } & {\delta_{44} } & {\delta_{45} } & {\delta_{46} } & {\delta_{47} } & {\delta_{48} } & {\delta_{49} } \\ {\delta_{15} } & {\delta_{45} } & {\delta_{55} } & {\delta_{56} } & {\delta_{57} } & {\delta_{58} } & {\delta_{59} } \\ {\delta_{16} } & {\delta_{46} } & {\delta_{56} } & {\delta_{66} } & {\delta_{67} } & {\delta_{68} } & {\delta_{69} } \\ {\delta_{17} } & {\delta_{47} } & {\delta_{57} } & {\delta_{67} } & {\delta_{77} } & {\delta_{78} } & {\delta_{79} } \\ {\delta_{18} } & {\delta_{48} } & {\delta_{58} } & {\delta_{68} } & {\delta_{78} } & {\delta_{88} } & {\delta_{89} } \\ {\delta_{19} } & {\delta_{49} } & {\delta_{59} } & {\delta_{69} } & {\delta_{79} } & {\delta_{89} } & {\delta_{99} } \\ \end{array} }} \right] \quad \Delta_{pq} =\left[ {{\begin{array}{*{20}c} {\delta_{1p} +\delta_{1q} } \\ {\delta_{4p} +\delta_{4q} } \\ {\delta_{5p} +\delta_{5q} } \\ {\delta_{6p} +\delta_{6q} } \\ {\delta_{7p} +\delta_{7q} } \\ {\delta_{8p} +\delta_{8q} } \\ {\delta_{9p} +\delta_{9q} } \\ \end{array} }} \right] \quad X=-\Delta_{1}^{-1}\cdot \Delta_{pq} =\left[ {{\begin{array}{*{20}c} {X_{1} } \\ {X_{4} } \\ {X_{5} } \\ {X_{6} } \\ {X_{7} } \\ {X_{8} } \\ {X_{9} } \\ \end{array} }} \right] \] \[ \text {Определение внутренних усилий } \] \[ M_{1} =M_{11} \cdot X_{1} ; \quad N_{12} =N_{121} \cdot X_{1} +N_{124} \cdot X_{4} +N_{12p} +N_{12q} ; \] \[ M_{2} =M_{21} \cdot X_{1} +M_{24} \cdot X_{4} +M_{2p} +M_{2q} ; \quad N_{23} =N_{231} \cdot X_{1} +N_{234} \cdot X_{4} +N_{23p} +N_{23q} ; \] \[ M_{3} =M_{31} \cdot X_{1} +M_{34} \cdot X_{4} +M_{3p} +M_{3q} ; \quad N_{34} =N_{341} \cdot X_{1} +N_{344} \cdot X_{4} +N_{34p} +N_{34q} ; \] \[ M_{4} =M_{44} \cdot X_{4} ; \quad N_{45} =N_{451} \cdot X_{1} +N_{454} \cdot X_{4} +N_{455} \cdot X_{5} +N_{45p} +N_{45q} ; \] \[ M_{5} =M_{55} \cdot X_{5} ; \quad N_{56} =N_{561} \cdot X_{1} +N_{564} \cdot X_{4} +N_{565} \cdot X_{5} +N_{566} \cdot X_{6} +N_{56p} +N_{56q} ; \] \[ M_{6} =M_{66} \cdot X_{6} ; \quad N_{67} =N_{671} \cdot X_{1} +N_{674} \cdot X_{4} +N_{676} \cdot X_{6} +N_{677} \cdot X_{7} +N_{67p} +N_{67q} ; \] \[ M_{7} =M_{77} \cdot X_{7} ; \quad N_{78} =N_{781} \cdot X_{1} +N_{784} \cdot X_{4} +N_{787} \cdot X_{7} +N_{788} \cdot X_{8} +N_{78p} +N_{78q} ; \] \[ M_{8} =M_{88} \cdot X_{8} ; \quad N_{89} =N_{891} \cdot X_{1} +N_{894} \cdot X_{4} +N_{898} \cdot X_{8} +N_{899} \cdot X_{9} +N_{89p} +N_{89q} ; \] \[ M_{9} =M_{99} \cdot X_{9} . \] \[ \text {Определение упругих реакций }\] \[ R_{1} =R_{2} =R_{3} =0; \] \[ R_{4} =R_{41} \cdot X_{1} +R_{44} \cdot X_{4} +R_{45} \cdot X_{5} +R_{4p} +R_{4q} ; \] \[ R_{5} =R_{51} \cdot X_{1} +R_{54} \cdot X_{4} +R_{55} \cdot X_{5} +R_{56} \cdot X_{6} +R_{5p} +R_{5q} ; \] \[ R_{6} =R_{61} \cdot X_{1} +R_{64} \cdot X_{4} +R_{65} \cdot X_{5} +R_{66} \cdot X_{6} +R_{67} \cdot X_{7} +R_{6p} +R_{6q} ; \] \[ R_{7} =R_{71} \cdot X_{1} +R_{74} \cdot X_{4} +R_{76} \cdot X_{6} +R_{77} \cdot X_{7} +R_{78} \cdot X_{8} +R_{7p} +R_{7q} ; \] \[ R_{8} =R_{81} \cdot X_{1} +R_{84} \cdot X_{4} +R_{87} \cdot X_{7} +R_{88} \cdot X_{8} +R_{89} \cdot X_{9} +R_{8p} +R_{8q} ; \] \[ R_{9} =R_{91} \cdot X_{1} +R_{94} \cdot X_{4} +R_{98} \cdot X_{8} +R_{99} \cdot X_{9} +R_{9p} +R_{9q} . \]