Гибкая квадратная шарнирно опертая по периметру пластина, нагруженная поперечной равномерно распределенной нагрузкой

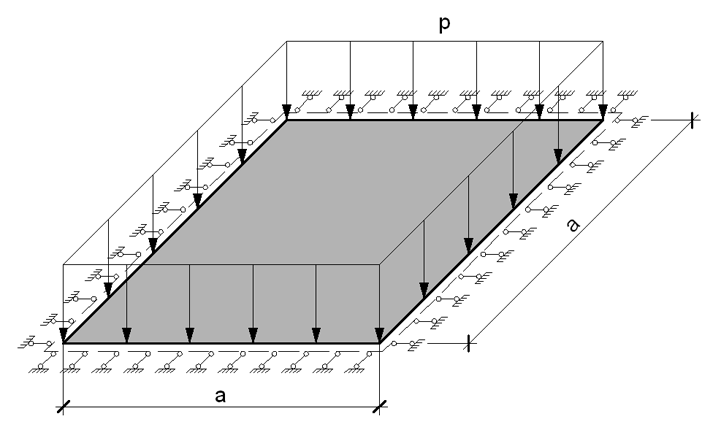
Цель: Определение максимальных перемещений и продольных напряжений в гибкой квадратной пластине, шарнирно опертой по периметру и нагруженной поперечной равномерно распределенной нагрузкой в геометрически нелинейной постановке.

Файл с исходными данными: 7.6.spr

Формулировка задачи: Гибкая квадратная изотропная пластина постоянной толщины шарнирно неподвижно оперта по периметру и нагружена поперечной равномерно распределенной нагрузкой p. Определить: поперечные перемещения w и продольные напряжения N_x и N_y для центра пластины.

Ссылки: S. Levy, Bending of rectangular plates with large deflections, Washington, National advisory committee for aeronautics, Technical note No 846, May 1942.

H. Hencky, Die berechnung dünner rechteckiger platten mit verschwindender biegungsteifigkeit, Dresden, Zeitschrift für angewandte mathematic und mechanic, April 1921.

И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания. Справочник в трех томах. Том 1, Москва, Машиностроение, 1968, стр. 606

Исходные данные:

E = 2.0·108 кПа	- модуль упругости материала пластины;
ν = 0.3	- коэффициент Пуассона;
h = 0.01 м	- толщина пластины;
a = 10.0 м	- размер стороны пластины;
p = 10 кПа	- значение равномерно распределенной нагрузки.

Конечноэлементная модель: Расчетная  схема – система общего вида. Элементы пластины - 10000 четырехузловых элементов оболочки с учетом геометрической нелинейности типа 344. Сетка конечных элементов разбита по длинам сторон пластины (вдоль осей X, Y общей системы координат) с шагом 0.10 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорного контура пластины по направлению степени свободы Z, а также за счет наложения связей на узлы сторон пластины по нормальному к ним направлению (для двух противоположных сторон параллельных оси Х общей системы координат – вдоль оси Y, для двух противоположных сторон параллельных оси Y общей системы координат – вдоль оси X). В целях обеспечения геометрической неизменяемости расчетной схемы на узел центра пластины накладывается связь по направлению UZ общей системы координат. Нелинейное загружение формировалось для шагово-итерационного метода с коэффициентом загружения - 1, количеством шагов - 1, количеством итераций - 100 для линейного загружения p. Количество узлов в расчетной схеме – 10201.

Результаты решения в SCAD

Расчетная схема

 

Деформированная схема

 

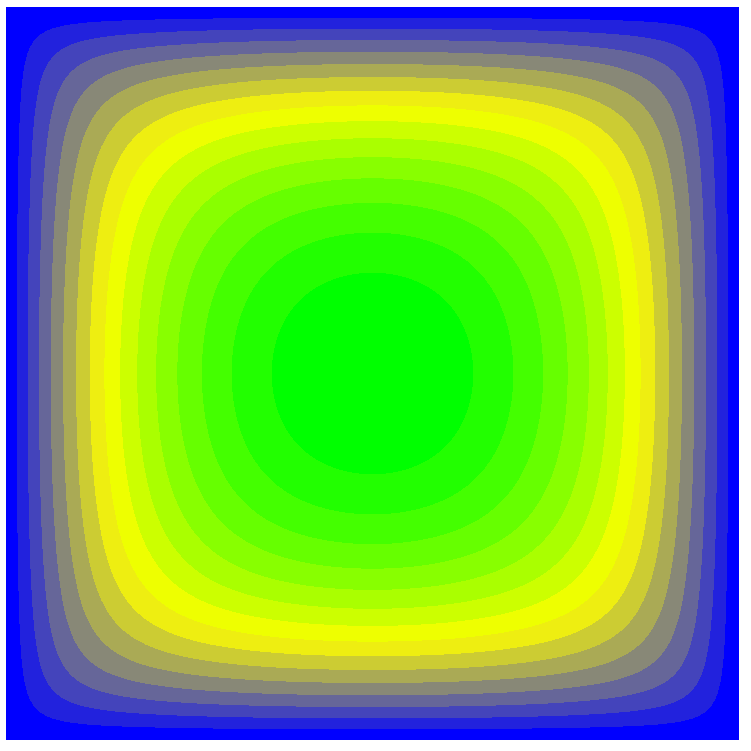
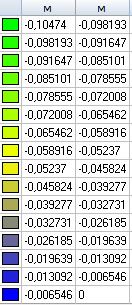
Значения поперечных перемещений w (м)

 

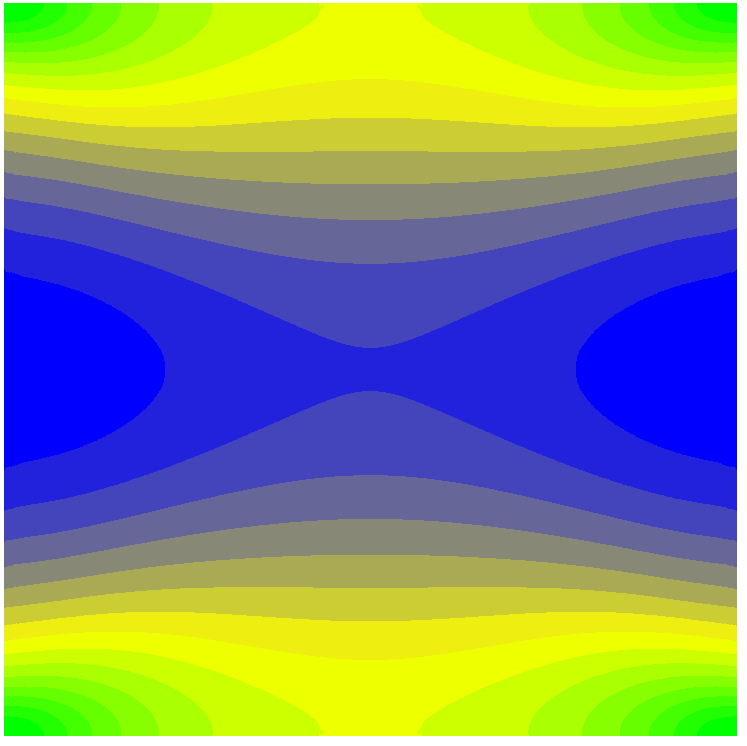
Значения продольных напряжений N_x (кН/м²)

 

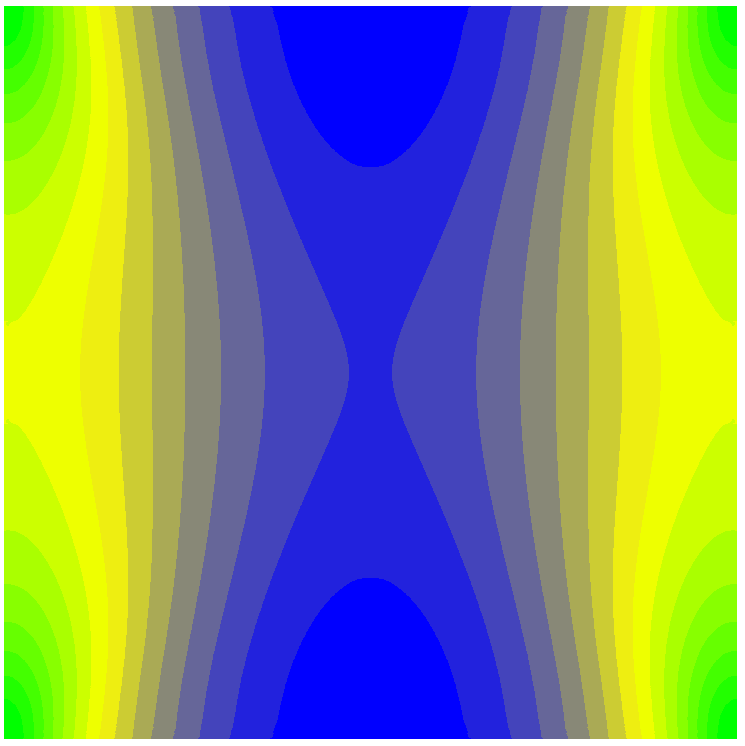
Значения продольных напряжений N_y (кН/м²)

Сравнение решений:

Параметр	Теория	SCAD	Отклонение, %
Поперечное перемещение в центре пластины w, м	0.1050 (0.1067)	0.1047	0.29 (1.87)
Продольное напряжение в центре пластины Nx, кН/м2	74963 (75830)	74480	0.64 (1.7)
Продольное напряжение в центре пластины Ny, кН/м2	74963 (75830)	74480	0.64 (1.7)

Без скобок указаны значения по приближенному решению Hencky для теории Кармана;
В скобках указаны значения по уточненному решению Levy для теории Кармана

Замечания: При аналитическом приближенном решении Hencky поперечные перемещения w и продольные напряжения N_x и N_y для центра пластины определяются по следующим формулам (коэффициент Пуассона ν = 0.3):

\[ w=0.285\cdot a\cdot \sqrt[3]{\frac{p}{E}\cdot \frac{a}{h}}; \quad N_{x} =N_{y} =3.4\cdot E\cdot \left( {\frac{w}{a}} \right)^{2}. \]