Гибкая круговая шарнирно опертая по контуру пластина, нагруженная поперечной равномерно распределенной нагрузкой
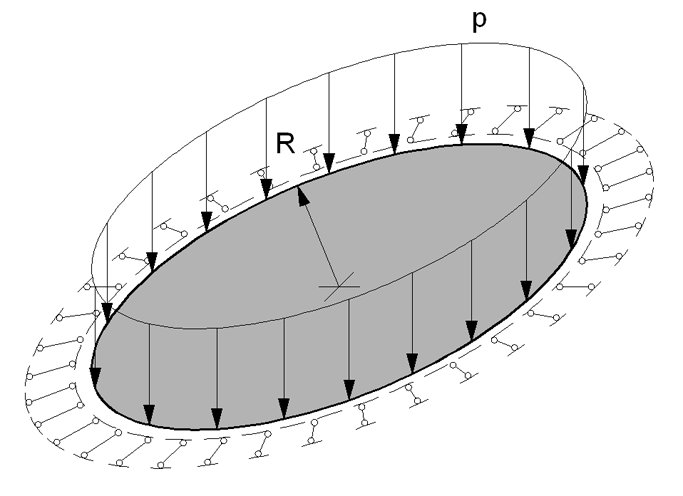
Цель: Определение максимальных перемещений и продольных радиально-кольцевых напряжений в гибкой круговой пластине, шарнирно опертой по контуру и нагруженной поперечной равномерно распределенной нагрузкой в геометрически нелинейной постановке.
Файл с исходными данными: 7.7.spr
Формулировка задачи: Гибкая круговая изотропная пластина постоянной толщины шарнирно неподвижно оперта по контуру и нагружена поперечной равномерно распределенной нагрузкой p. Определить: поперечные перемещения w и продольные радиально-кольцевые напряжения Nr и Nt для центра пластины.
Ссылки: S. Way, Bending of circular plates with large deflections, New York, ASME, v.56 N 8, 1934, p. 627-636.
H. Hencky, Uber den spannungsztand in kreisrunden platten mit verschwindender biegungssteifigkeit, Dresden, Zeitschrift für angewandte mathematic und physik, v.63, 1915, p. 311-317.
И. А. Биргер, Я. Г. Пановко, Прочность, устойчивость, колебания. Справочник в трех томах. Том 1, Москва, Машиностроение, 1968, стр. 614
Исходные данные:
| E = 2.0·108 кПа | - модуль упругости материала пластины; |
| ν = 0.3 | - коэффициент Пуассона; |
| h = 0.01 м | - толщина пластины; |
| R = 5.0 м | - наружный радиус пластины; |
| p = 10 кПа | - значение равномерно распределенной нагрузки. |
Конечноэлементная модель: Расчетная схема – система общего вида. Элементы пластины - 8820 четырехузловых элементов оболочки с учетом геометрической нелинейности типа 344 и 180 трехузловых элементов оболочки с учетом геометрической нелинейности типа 342. Сетка конечных элементов разбита с шагом 0.10 м в радиальном направлении и с шагом 2.0º в тангенциальном направлении. Направление выдачи внутренних усилий – радиально-тангенциальное. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Y и Z по наружному контуру пластины. В целях обеспечения геометрической неизменяемости расчетной схемы на узел центра пластины накладывается связь по направлению UZ общей системы координат. Нелинейное загружение формировалось для шагово-итерационного метода с коэффициентом загружения - 1, количеством шагов - 1, количеством итераций - 100 для линейного загружения p.Количество узлов в расчетной схеме – 9001.
Результаты решения в SCAD
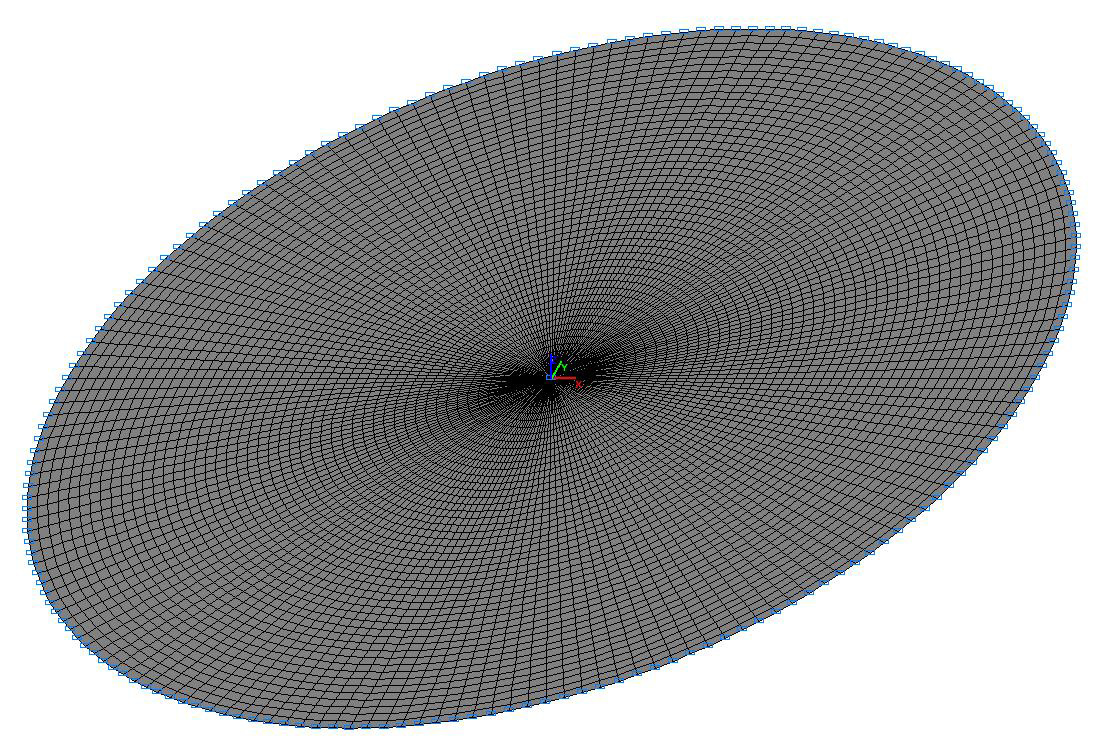

Расчетная схема
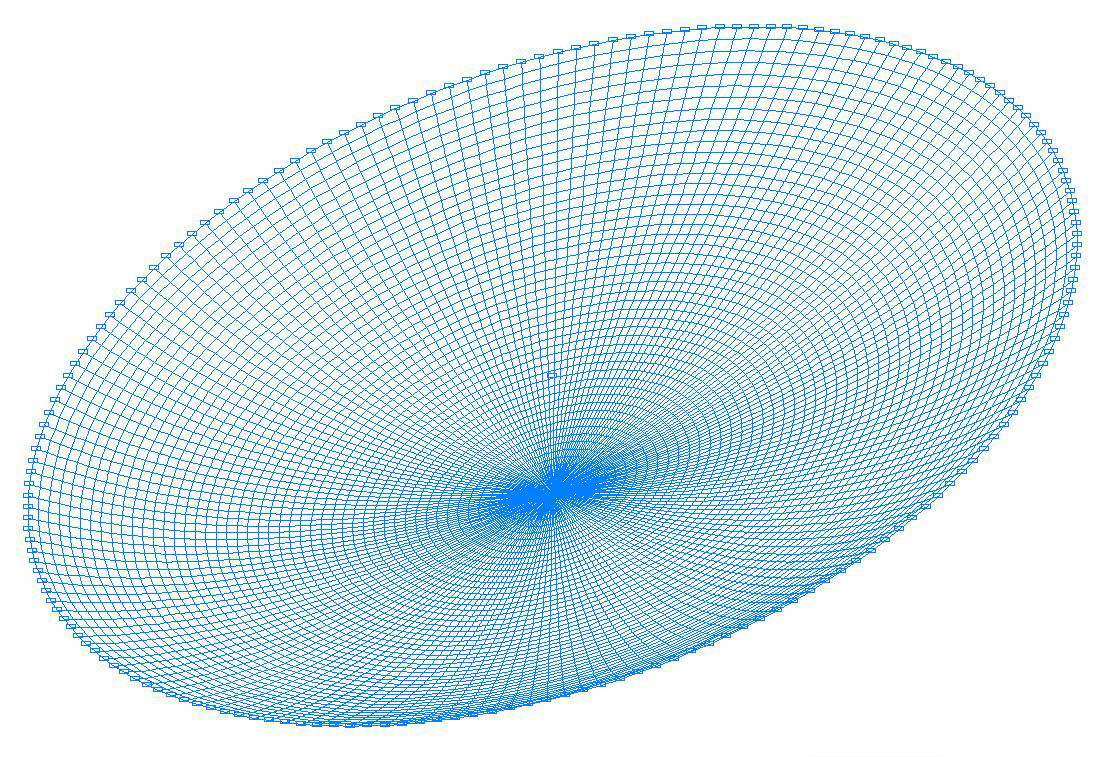

Деформированная схема
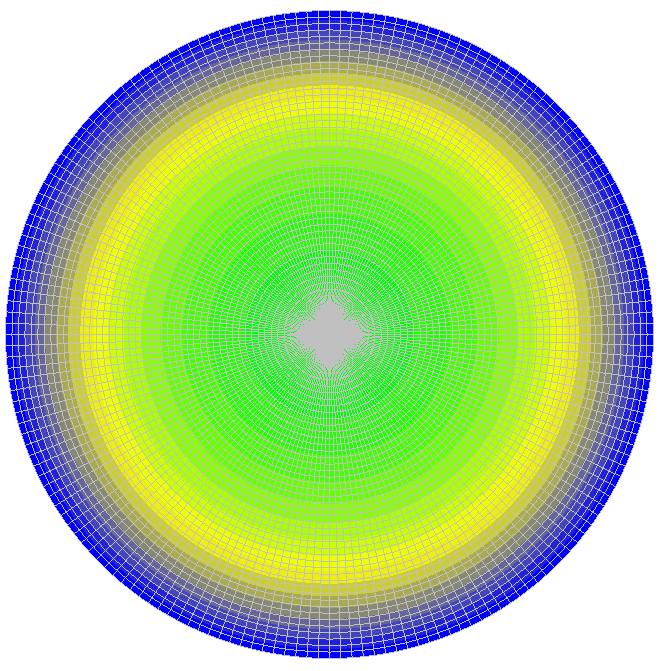

Значения поперечных перемещений w (м)
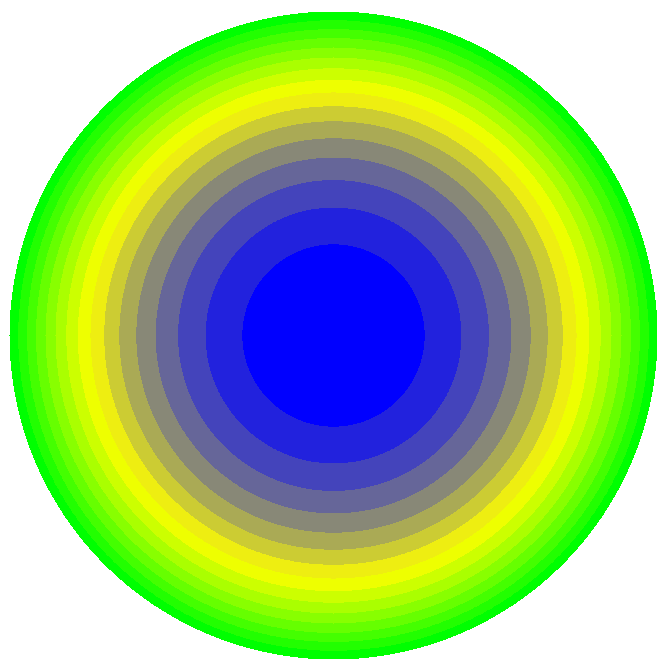
Значения продольных радиальных напряжений Nr (кН/м2)
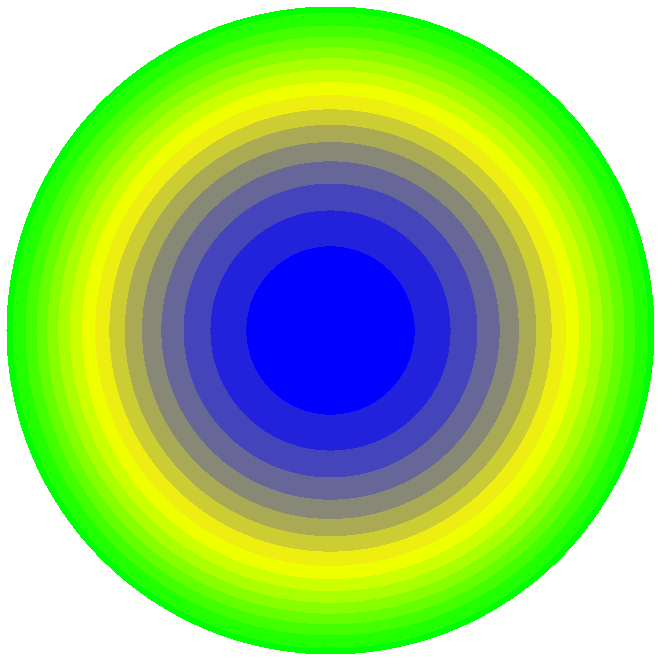
Значения продольных тангенциальных напряжений Nt (кН/м2)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Поперечное перемещение в центре пластины w, м |
0.0968 |
0.0957 |
1.14 |
|
Продольное радиальное напряжение в центре пластины Nr, кН/м2 |
72316 |
73540 |
1.69 |
|
Продольное тангенциальное напряжение в центре пластины Nt, кН/м2 |
72316 |
73540 |
1.69 |
Замечания: При аналитическом приближенном решении Hencky по теории Кармана поперечные перемещения w и продольные радиально-тангенциальные напряжения Nr и Nt для центра пластины определяются по следующим формулам (коэффициент Пуассона ν = 0.3):
\[ w=0.662\cdot R\cdot \sqrt[3]{\frac{p}{E}\cdot \frac{R}{h}}; \quad N_{r} =N_{t} =0.965\cdot E\cdot \left( {\frac{w}{R}} \right)^{2}. \]