Гибкое кольцо, нагруженное двумя взаимно уравновешенными радиально сжимающими силами

Цель: Определение максимальных перемещений и изгибающих моментов в гибком кольце, нагруженном двумя взаимно уравновешенными радиально сжимающими силами в геометрически нелинейной постановке.

 

Файлы с исходными данными:

Кольцо_Q_50.spr

Гибкое кольцо нагружено радиально сжимающими силами Q = 50 кН

 

Формулировка задачи: Гибкое кольцо постоянного поперечного сечения нагружено двумя взаимно уравновешенными радиально сжимающими силами Q. Определить: поперечные перемещения w и изгибающие моменты M в местах приложения сжимающих сил.

Ссылки: Е. П. Попов, Теория и расчет гибких упругих стержней, Москва, Наука, 1986, стр. 154

Исходные данные:

EF = 1.5·107 кН	- продольная жесткость поперечного сечения кольца;
EIy = 3.125·105 кН•м2	- изгибная жесткость поперечного сечения кольца в его плоскости;
EIz = 1.250·106 кН•м2	- изгибная жесткость поперечного сечения кольца из его плоскости;
GIx = 3.533·105 кН•м2	- крутильная жесткость поперечного сечения кольца;
R = 50.0 м	- радиус кольца;
Q = 50 кН	- значение сжимающих сил.

Конечноэлементная модель: Расчетная  схема – система общего вида. Элементы пластины - 180 стержневых элементов с учетом геометрической нелинейности типа 310. Сетка конечных элементов разбита по длине продольной оси кольца с шагом 2.0º. Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связей по условиям ее симметрии. Нелинейное загружение формировалось для шагово-итерационного метода с коэффициентом загружения - 1, количеством шагов - 1, количеством итераций - 7 для линейного загружения Q. Количество узлов в расчетной схеме – 180.

Результаты решения в SCAD

Расчетная схема

 

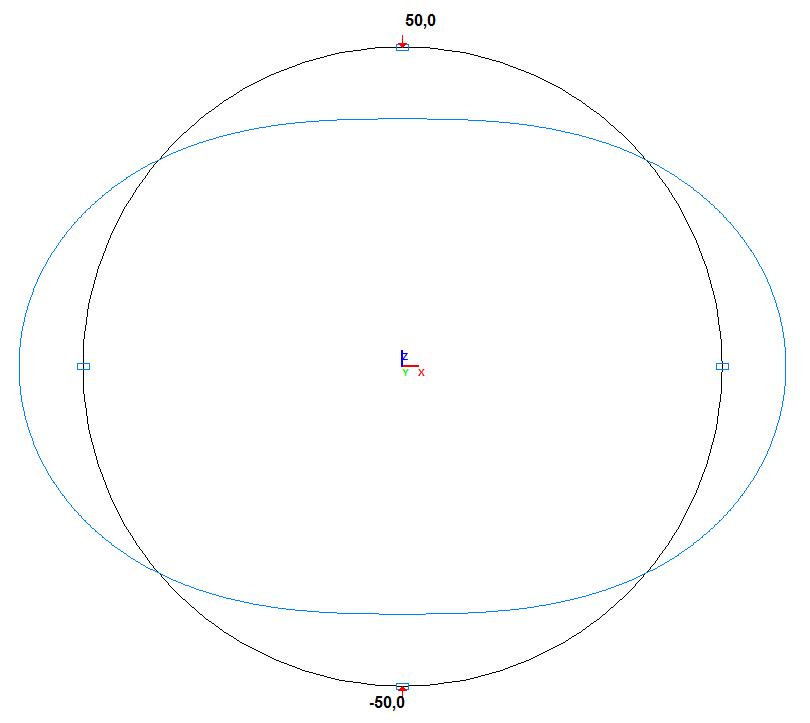
Деформированная схема

 

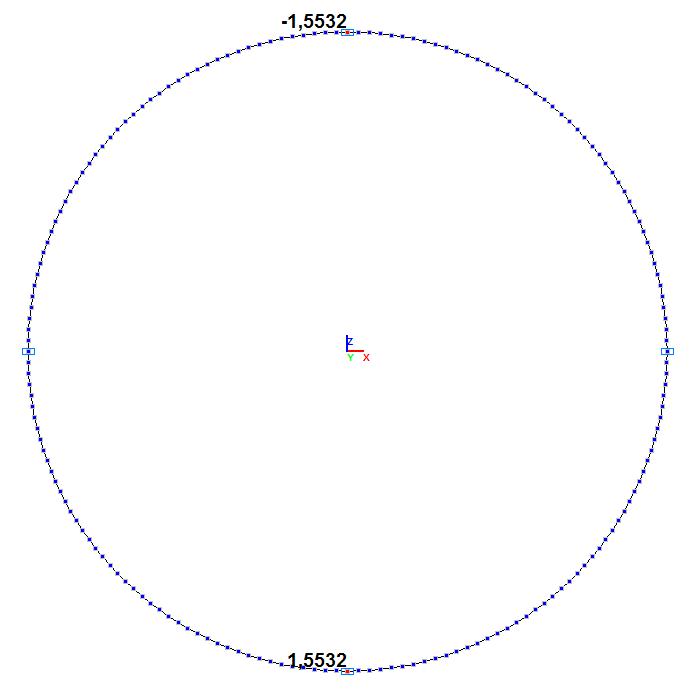
Значения поперечных перемещений w (м)

 

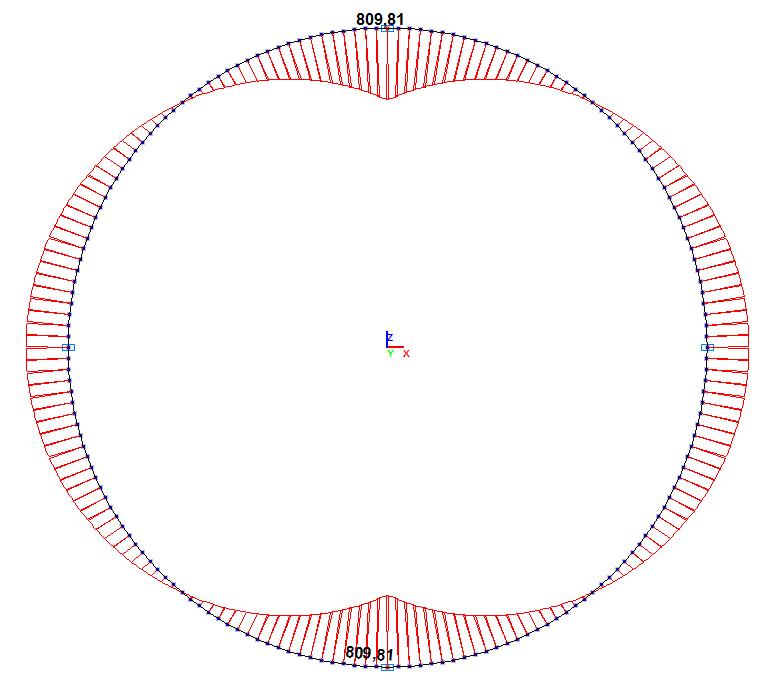
Эпюры изгибающих моментов M (кН∙м)

Сравнение решений:

Параметр	Теория	SCAD	Отклонение, %
Поперечное перемещение сечения кольца w, м в местах приложения сжимающих сил Q = 50 кН	±1.6060	±1.5532	3.29
Изгибающий момент для сечения кольца M, кН∙м в местах приложения сжимающих сил Q = 50 кН	809.37	809.81	0.05

Замечания: При аналитическом решении поперечные перемещения w и изгибающие моменты M в местах приложения сжимающих сил определяются по следующим формулам:

\[
При \quad 0\le Q\le 0.6297\cdot \frac{EI}{R^{2}}:
\]
\[
w=\left[ {\frac{2}{k}\cdot \sqrt {\frac{2\cdot EI}{Q\cdot R^{2}}} \cdot
E\left( {\frac{\pi }{4}} \right)-\left( {\frac{2}{k^{2}}-1} \right)\cdot
\frac{\pi }{2}} \right]\cdot R;
\quad
M=\frac{2}{k}\cdot \sqrt {1-\frac{k^{2}}{2}} \cdot \sqrt {\frac{Q\cdot
EI}{2}} -\frac{EI}{R},
\]
\[
\text { где k определяется из решения уравнения:} k\cdot F\left( {\frac{\pi }{4}}
\right)=\frac{\pi \cdot R}{2}\cdot \sqrt {\frac{Q}{2\cdot EI}} ;
\]
\[
F\left( {\frac{\pi }{4}} \right)=\int\limits_0^{\frac{\pi }{4}} {\frac{d\phi
}{\sqrt {1-k^{2}\cdot \sin^{2}\left( \phi \right)} }} - \quad \text { эллиптический интеграл Лежандра первого рода,}
\]
\[
E\left( {\frac{\pi }{4}} \right)=\int\limits_0^{\frac{\pi }{4}} {\sqrt
{1-k^{2}\cdot \sin^{2}\left( \phi \right)} \cdot d\phi -} \quad \text { эллиптический интеграл Лежандра второго рода.}
\]
\[
При \quad 0.6297\cdot \frac{EI}{R^{2}}\le Q\le 2.7865\cdot \frac{EI}{R^{2}}:
\]
\[
w=\left[ {2\cdot \sqrt {\frac{2\cdot EI}{Q\cdot R^{2}}} \cdot E\left( \Psi
\right)-\frac{\pi }{2}} \right]\cdot R;
\quad
M=2\cdot k\cdot \cos \left( \Psi \right)\cdot \sqrt {\frac{Q\cdot EI}{2}}
-\frac{EI}{R},
\]
\[
где \quad k \quad и \quad \Psi \quad \text {определяются из решения системы уравнений:} \quad \left\{
{{\begin{array}{*{20}c}
 {k\cdot \sin \left( \Psi \right)=\frac{\sqrt 2 }{2}}  \\
 {F\left( \Psi \right)=\frac{\pi \cdot R}{2}\cdot \sqrt {\frac{Q}{2\cdot
EI}} }  \\
\end{array} }} \right.;
\]
\[
F\left( \Psi \right)=\int\limits_0^\Psi {\frac{d\psi }{\sqrt {1-k^{2}\cdot
\sin^{2}\left( \psi \right)} }} -\quad \text { эллиптический интеграл Лежандра первого}
рода,
\]
\[
E\left( \Psi \right)=\int\limits_0^\Psi {\sqrt {1-k^{2}\cdot \sin^{2}\left(
\psi \right)} \cdot d\psi } \quad - \text { эллиптический интеграл Лежандра второго рода.}
\]