Прямоугольная пластина в условиях постоянных напряжений на срединной поверхности

Цель: Проверка точного воспроизведения условий постоянных напряжений на срединной поверхности прямоугольной пластины при нерегулярной крупной сетке конечных элементов.

Файлы с исходными данными:

Patch_test_Constant_stress_Shell_42.spr	Расчетная модель с типом элементов 42
Patch_test_Constant_stress_Shell_44.spr	Расчетная модель с типом элементов 44
Patch_test_Constant_stress_Shell_45.spr	Расчетная модель с типом элементов 45
Patch_test_Constant_stress_Shell_50.spr	Расчетная модель с типом элементов 50

 

Формулировка задачи: Прямоугольная изотропная пластина постоянной толщины подвергается воздействию смещений наружных кромок, обеспечивающих условия постоянных напряжений на срединной поверхности. Проверить: обеспечение условий постоянных нормальных σ_x, σ_y и касательных τ_xy напряжений на срединной поверхности.

Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.

J. Robinson, S. Blackham, An evaluation of lower order membranes as contained in MSC/NASTRAN, ASAS and PARFEC FEM system, Dorset, Robinson and associates, 1979.

Исходные данные:

E = 1.0·106 кПа	- модуль упругости материала пластины;
ν = 0.25	- коэффициент Пуассона;
t = 0.001 м	- толщина пластины;
a = 0.12 м	- размер короткой стороны пластины;
b = 0.24 м	- размер длинной стороны пластины;

Граничные условия:

u = 10-3∙(x + y/2)	- смещение наружных кромок вдоль длинной стороны пластины;
v = 10-3∙(x/2 + y)	- смещение наружных кромок вдоль короткой стороны пластины;

Расположение внутренних узлов сетки конечных элементов:

Номера узлов по рисунку 1	x	y
1	0.04	0.02
2	0.18	0.03
3	0.16	0.08
4	0.08	0.08

 

Конечноэлементная модель: Расчетная  схема – система общего вида. Рассматриваются четыре расчетные модели:

 

Модель 1 - 10 трехузловых элементов оболочки типа 42. Обеспечение граничных условий достигается за счет наложения связей на узлы наружных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и смещения их в соответствии с заданными значениями u и v. Количество узлов в модели – 8.

Модель 2 - 5 четырехузловых элементов оболочки типа 44. Обеспечение граничных условий достигается за счет наложения связей на узлы наружных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и смещения их в соответствии с заданными значениями u и v. Количество узлов в модели – 8.

Модель 3 - 10 шестиузловых элементов оболочки типа 45. Обеспечение граничных условий достигается за счет наложения связей на узлы наружных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и смещения их в соответствии с заданными значениями u и v. Количество узлов в модели – 25.

Модель 4 - 5 восьмиузловых элементов оболочки типа 50. Обеспечение граничных условий достигается за счет наложения связей на узлы наружных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и смещения их в соответствии с заданными значениями u и v. Количество узлов в модели – 20

Результаты решения в SCAD

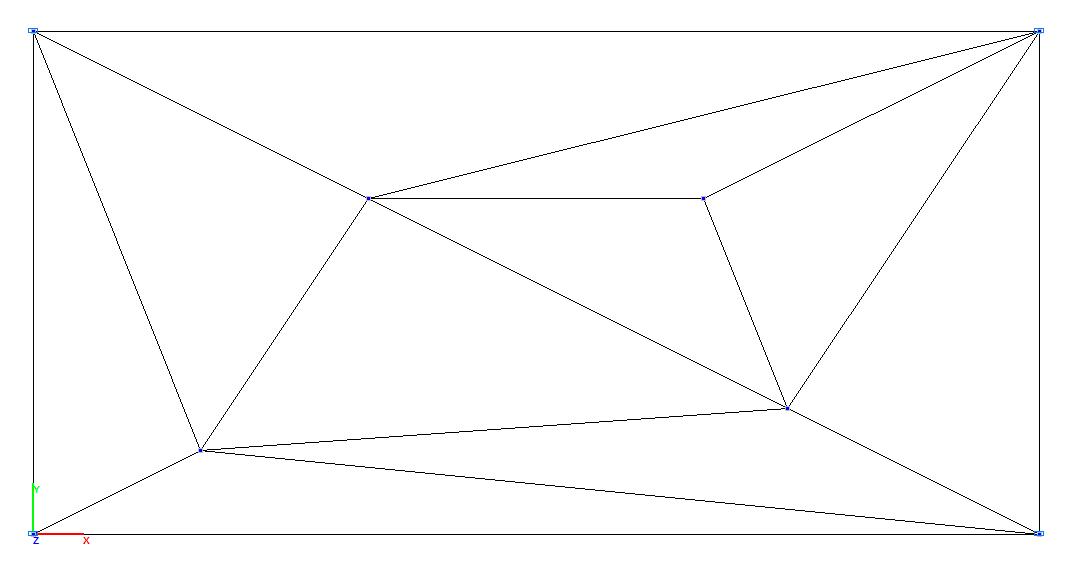
Модель 1. Расчетная схема

 

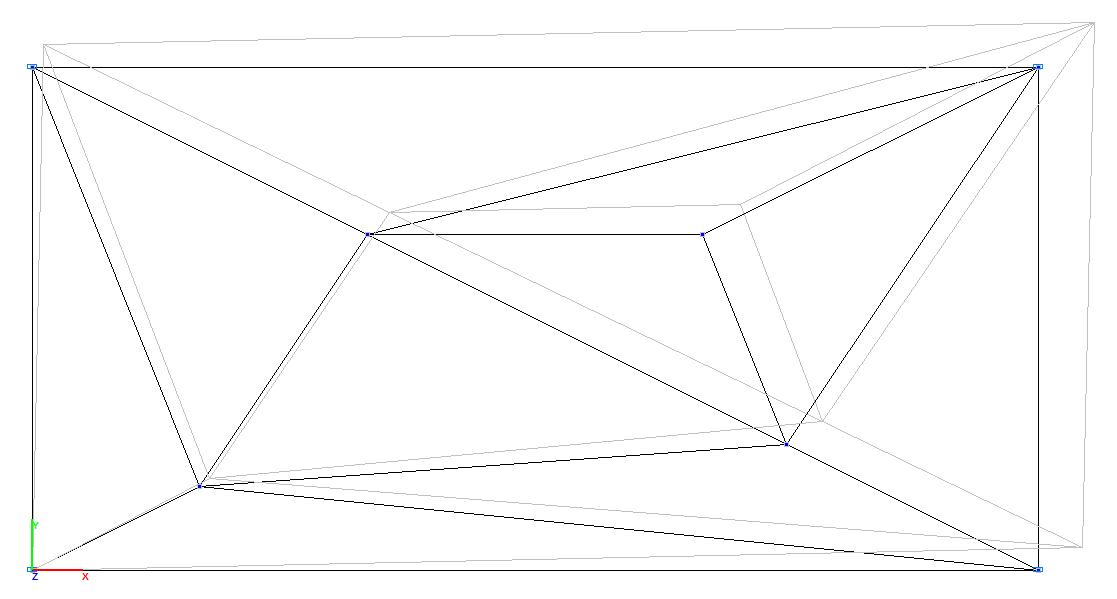
Модель 1. Деформированная схема

 

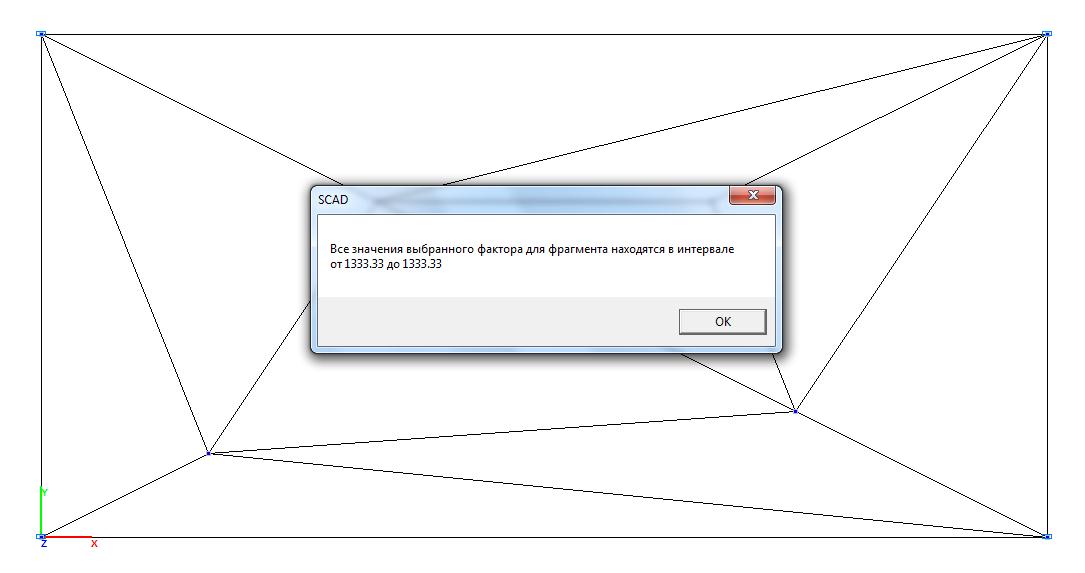
Модель 1. Значения нормальных напряжений σ_x (кН/м²)

 

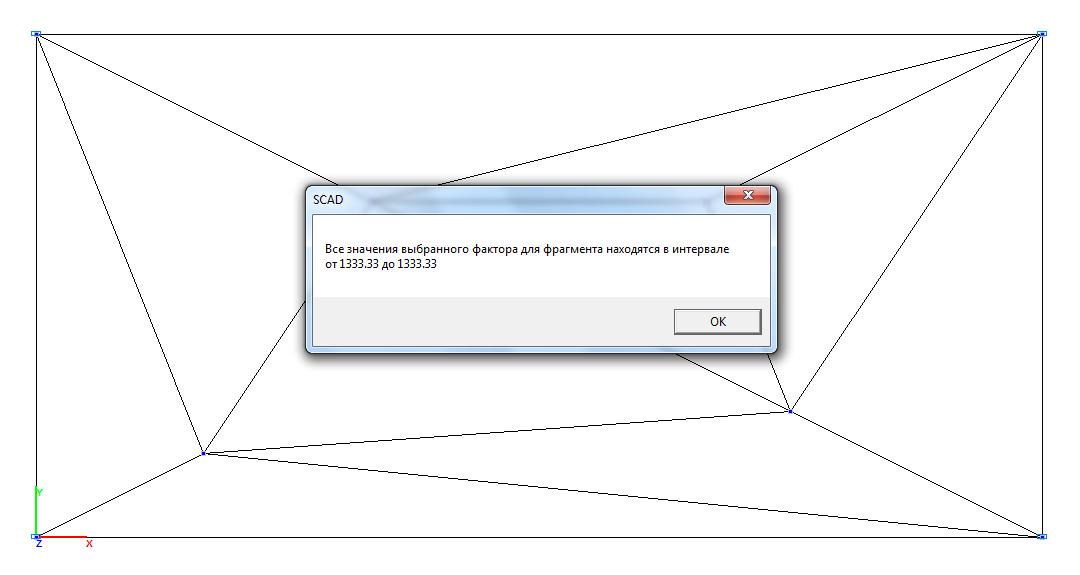
Модель 1. Значения нормальных напряжений σ_y (кН/м²)

 

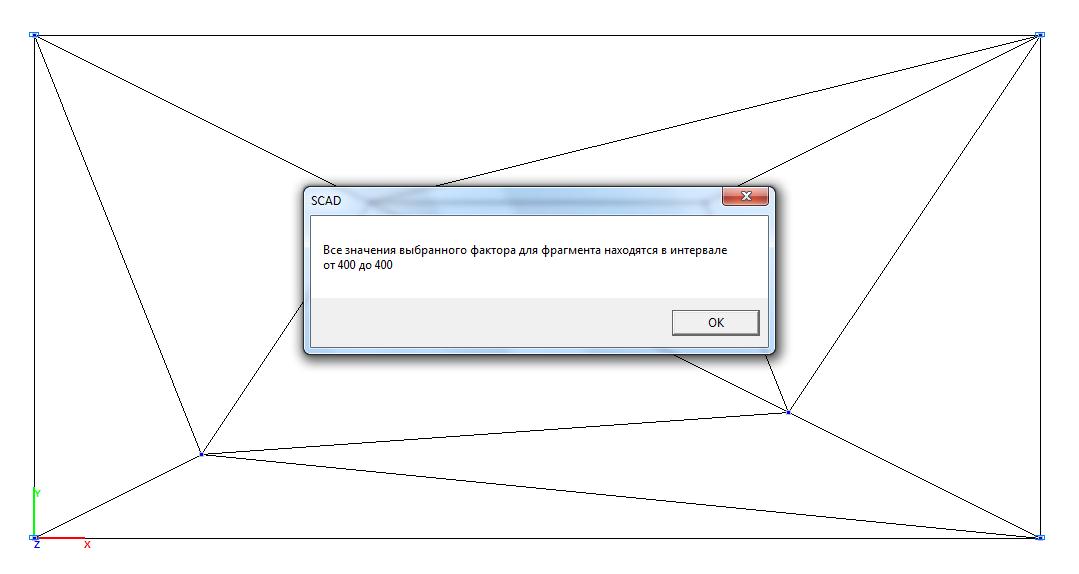
Модель 1. Значения касательных напряжений τ_xy (кН/м²)

 

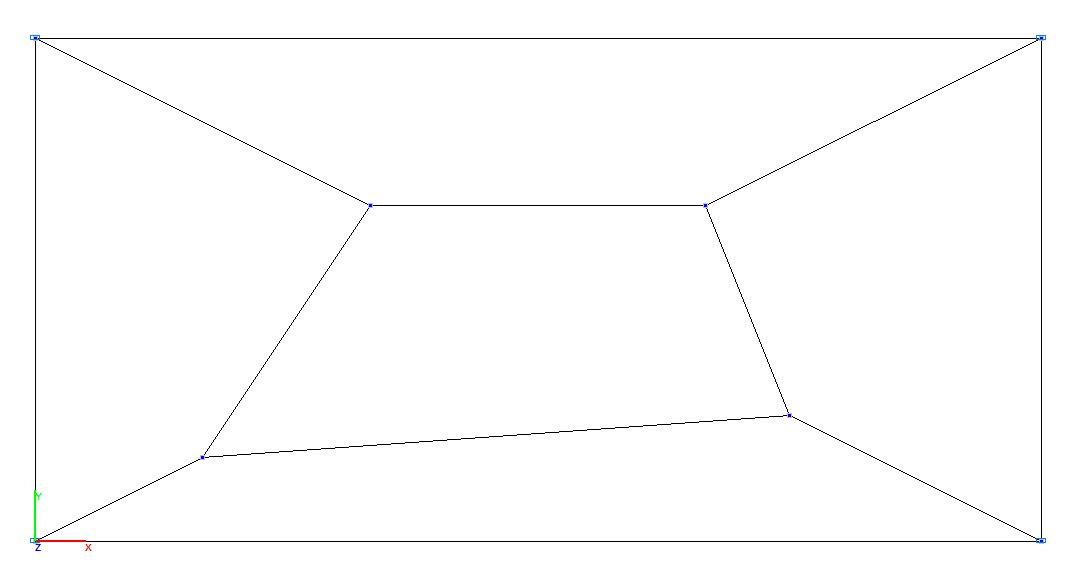
Рис. 7 Модель 2. Расчетная схема

 

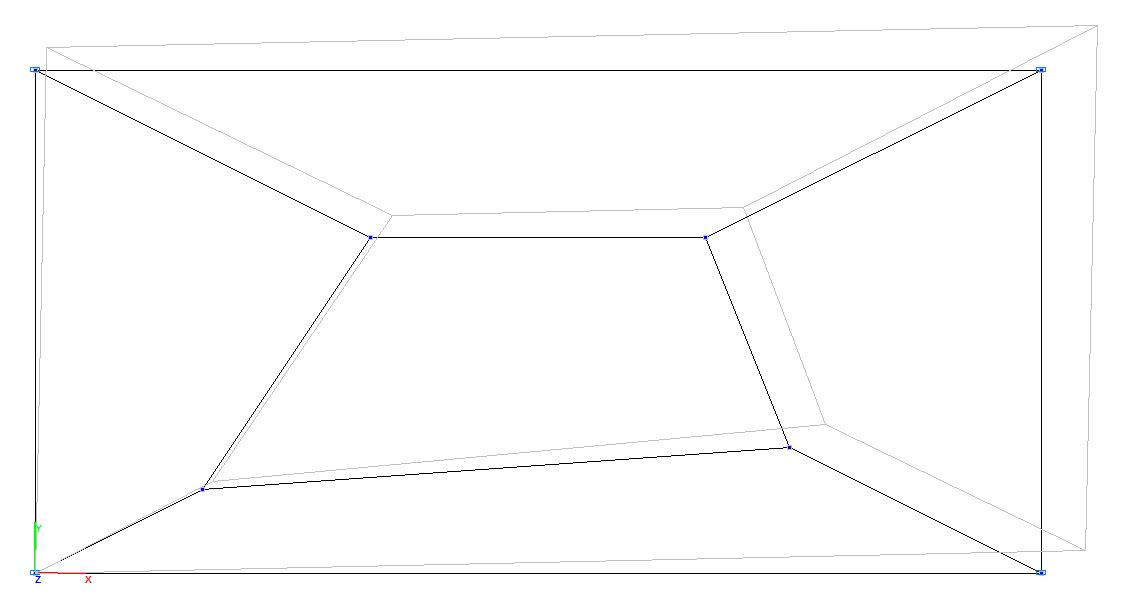
Модель 2. Деформированная схема

 

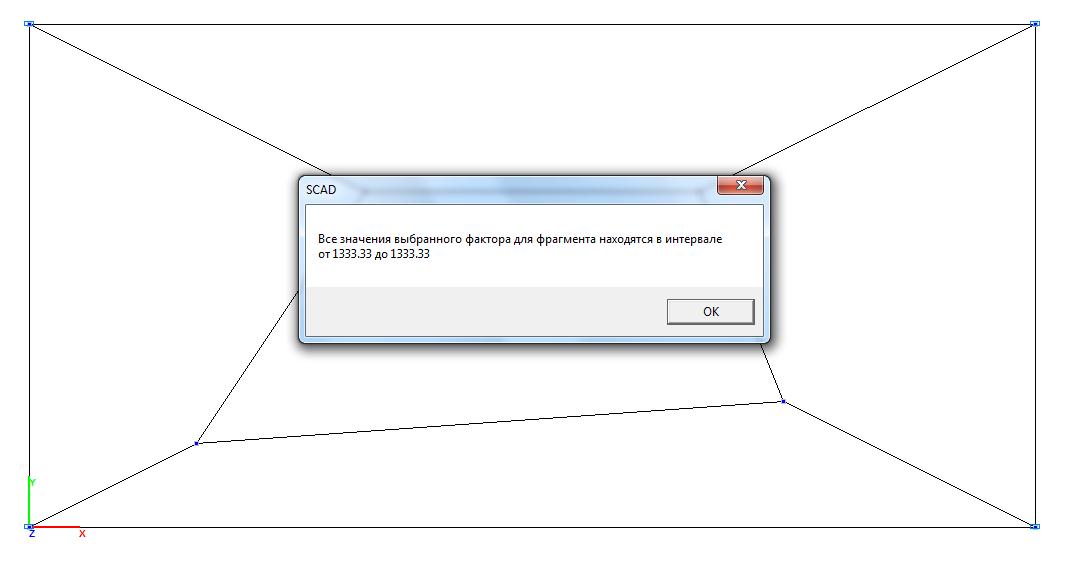
Модель 2. Значения нормальных напряжений σ_x (кН/м²)

 

Модель 2. Значения нормальных напряжений σ_y (кН/м²)

 

Модель 2. Значения касательных напряжений τ_xy (кН/м²)

 

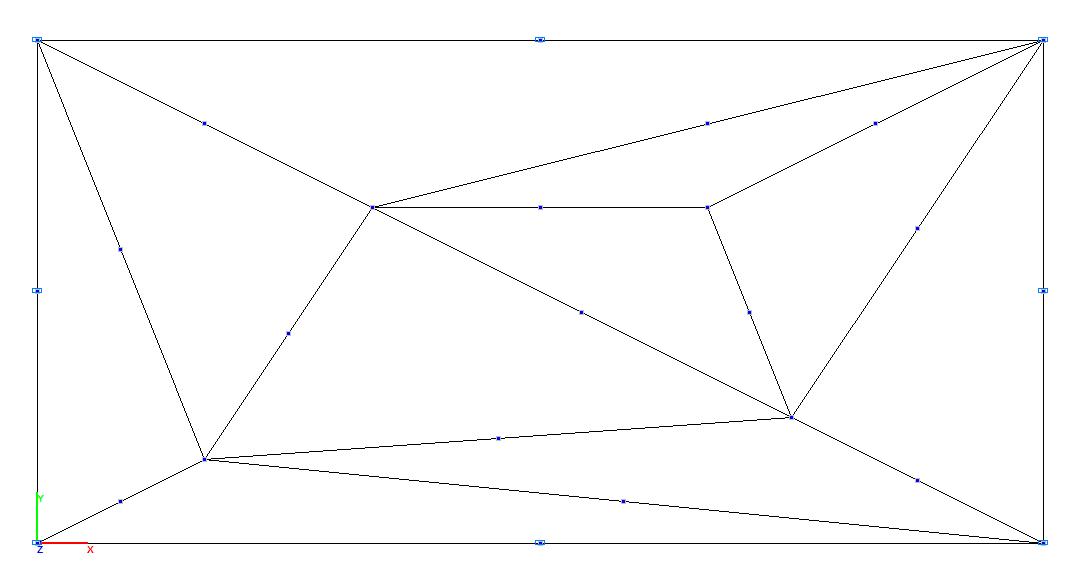
Модель 3. Расчетная схема

 

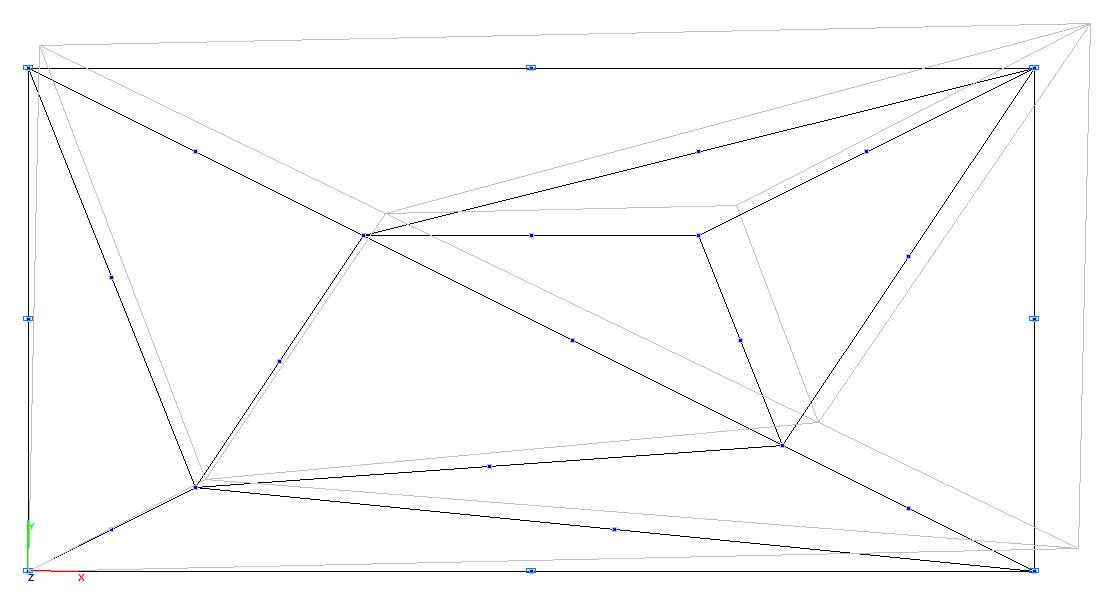
Модель 3. Деформированная схема

 

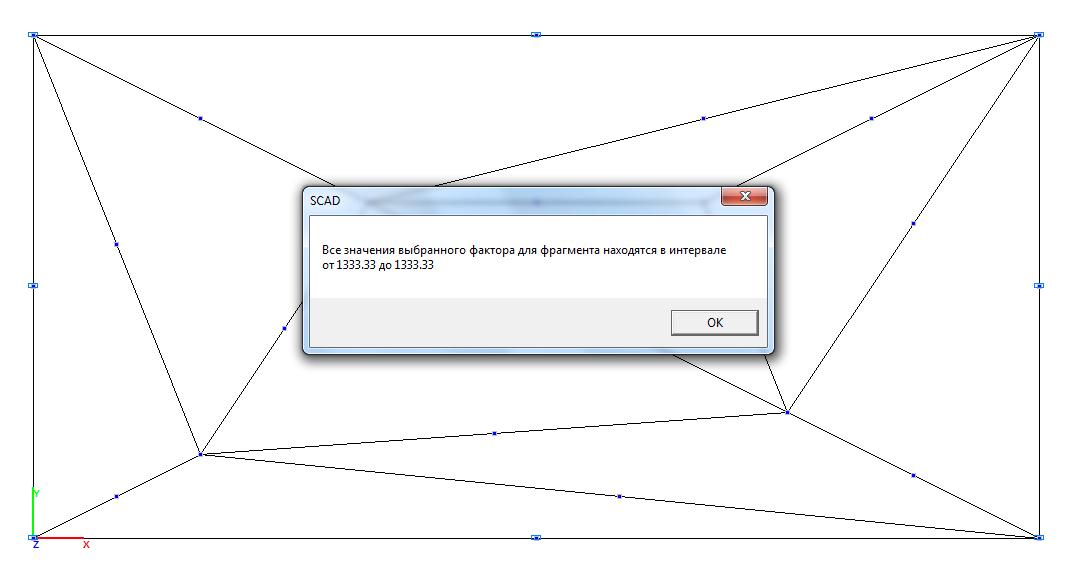
Модель 3. Значения нормальных напряжений σ_x (кН/м²)

 

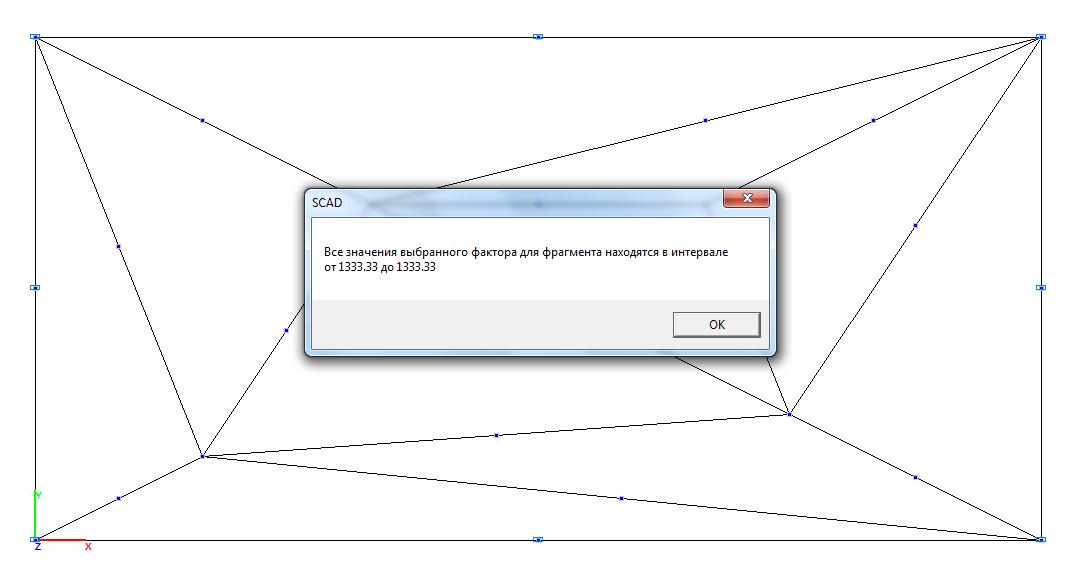
Модель 3. Значения нормальных напряжений σ_y (кН/м²)

 

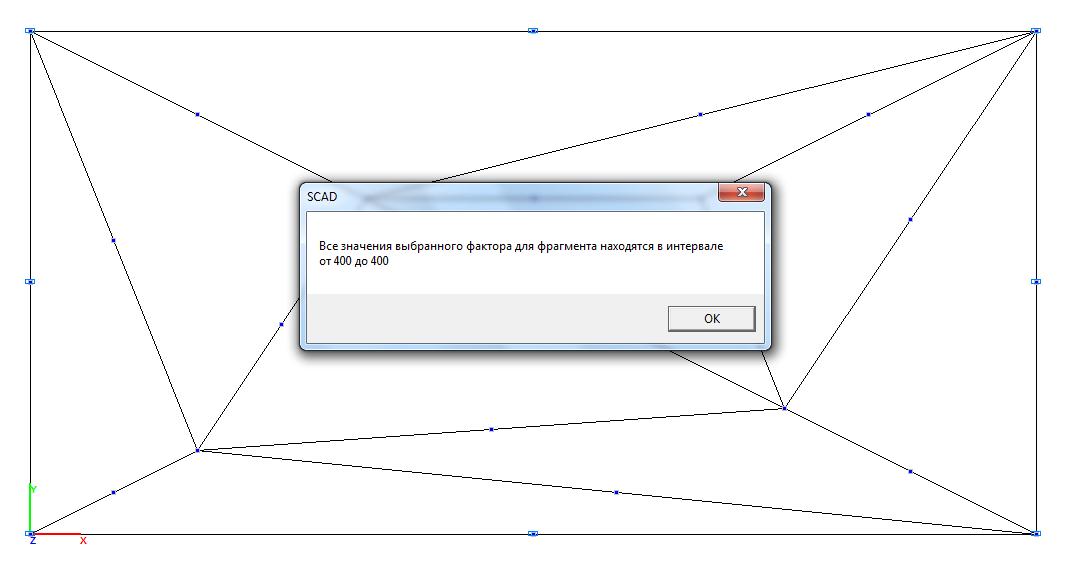
Модель 3. Значения касательных напряжений τ_xy (кН/м²)

 

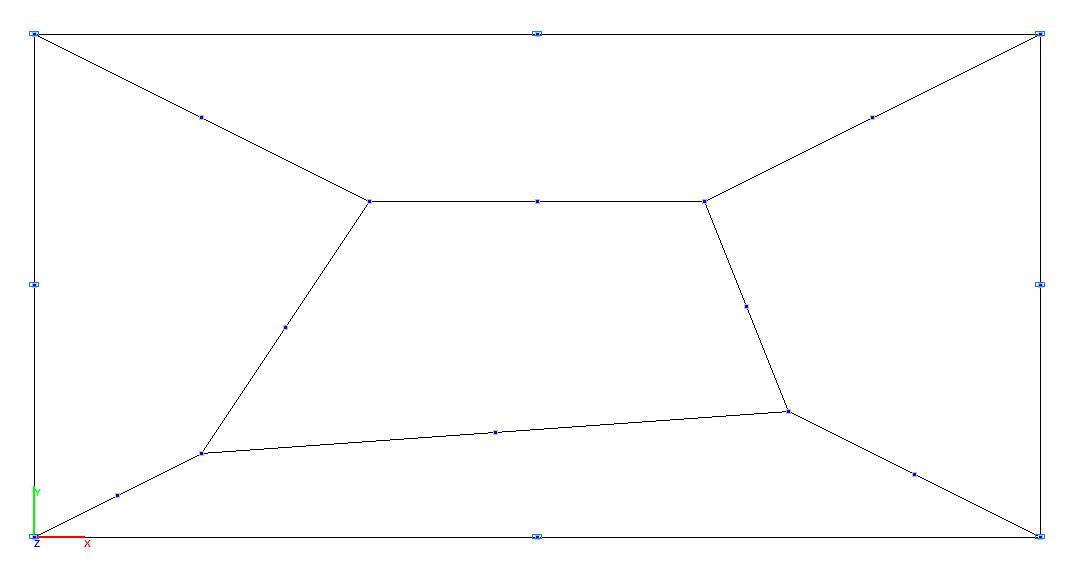
Модель 4. Расчетная схема

 

Модель 4. Деформированная схема

 

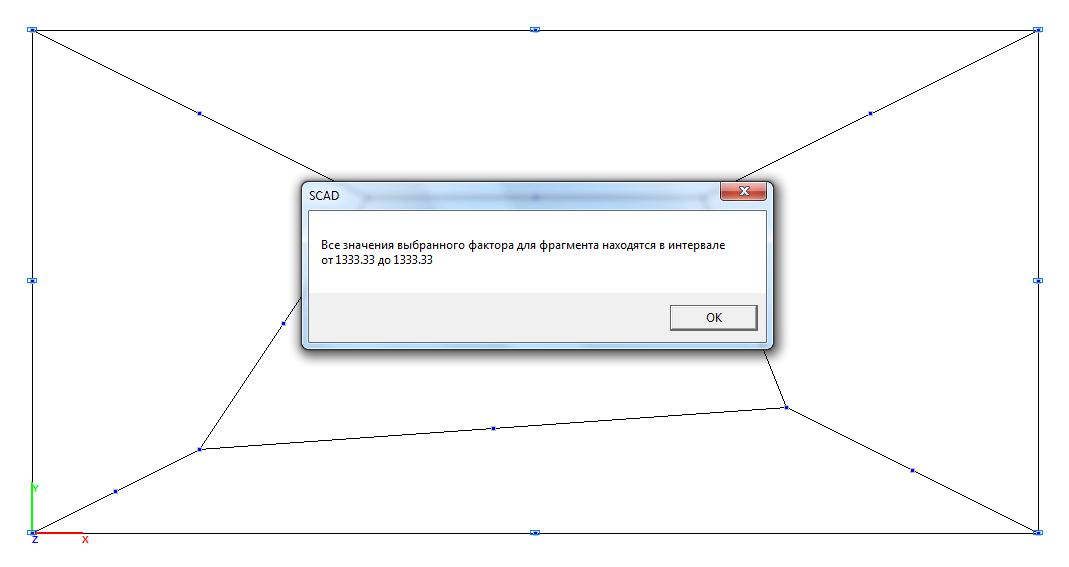
Модель 4. Значения нормальных напряжений σ_x (кН/м²)

 

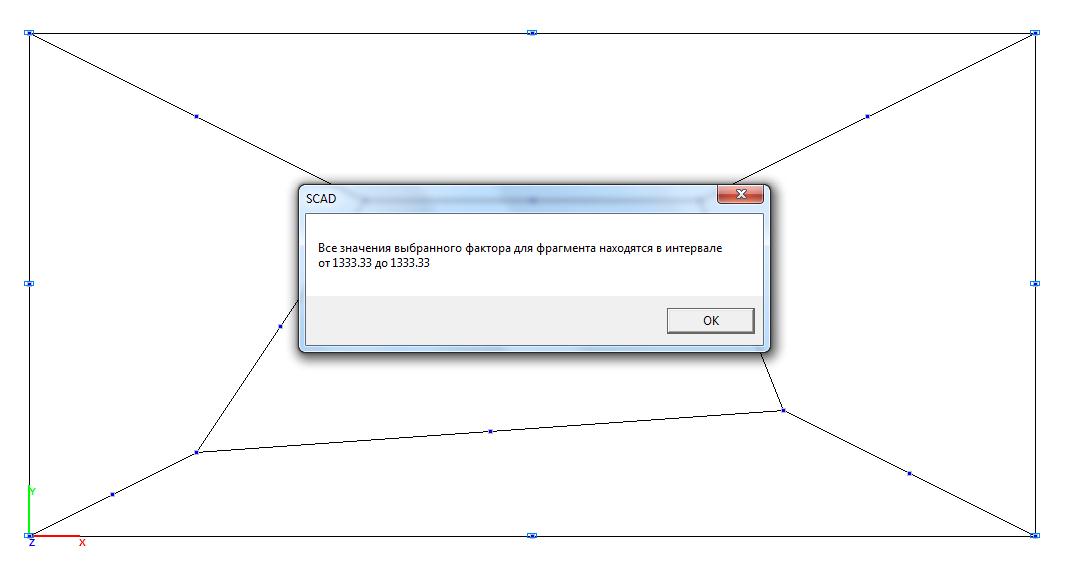
Модель 4. Значения нормальных напряжений σ_y (кН/м²)

 

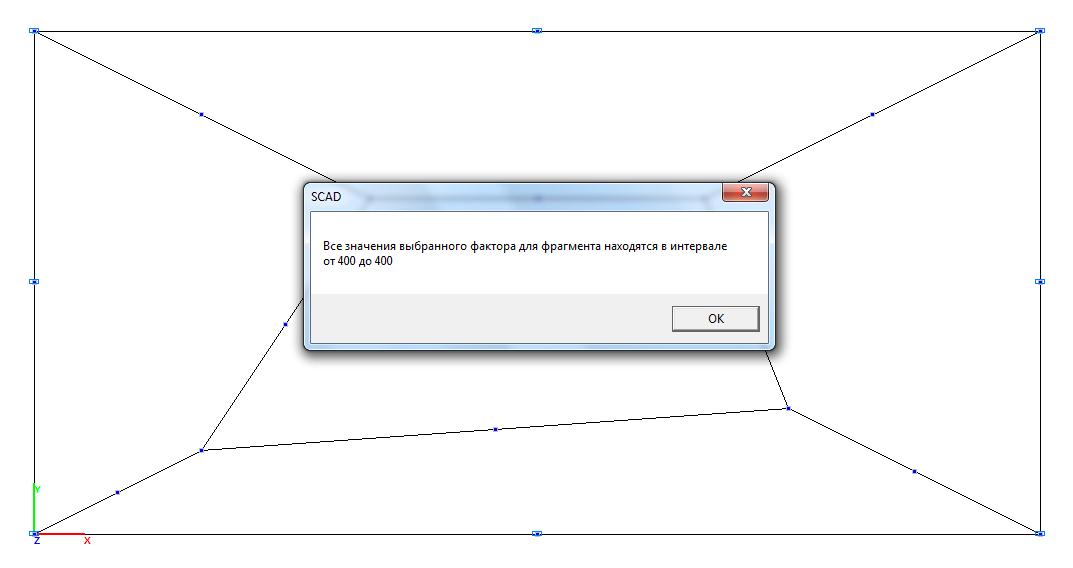
Модель 4. Значения касательных напряжений τ_xy (кН/м²)

Сравнение решений:

Модель	Параметр	Теория	SCAD	Отклонение, %
1	Нормальные напряжения σx, кН/м2	1333	1333	0.00
	Нормальные напряжения σy, кН/м2	1333	1333	0.00
	Касательные напряжения τxy, кН/м2	400	400	0.00
2	Нормальные напряжения σx, кН/м2	1333	1333	0.00
	Нормальные напряжения σy, кН/м2	1333	1333	0.00
	Касательные напряжения τxy, кН/м2	400	400	0.00
3	Нормальные напряжения σx, кН/м2	1333	1333	0.00
	Нормальные напряжения σy, кН/м2	1333	1333	0.00
	Касательные напряжения τxy, кН/м2	400	400	0.00
4	Нормальные напряжения σx, кН/м2	1333	1333	0.00
	Нормальные напряжения σy, кН/м2	1333	1333	0.00
	Касательные напряжения τxy, кН/м2	400	400	0.00

Замечания: При аналитическом решении нормальные σ_x, σ_y и касательные τ_xy напряжения на срединной поверхности пластины определяются по следующим формулам:

\[ \sigma_{x} =10^{-3}\cdot \frac{E}{1-\nu }; \quad \sigma_{y} =10^{-3}\cdot \frac{E}{1-\nu }; \quad \tau_{xy} =10^{-3}\cdot \frac{E}{2\cdot \left( {1+\nu } \right)}. \]