Криволинейная консольная балка под действием на свободном торце сосредоточенных поперечных сил
Цель: Проверка точного воспроизведения значений поперечных смещений свободного торца криволинейной консольной балки от действия на нем сосредоточенных соответствующих поперечных сил.
Файлы с исходными данными:
| Curved_cantilever_beam_Shell_42.spr | Расчетная модель с типом элементов 42 |
| Curved_cantilever_beam_Shell_142.spr | Расчетная модель с типом элементов 142 |
| Curved_cantilever_beam_Shell_44.spr | Расчетная модель с типом элементов 44 |
| Curved_cantilever_beam_Shell_144.spr | Расчетная модель с типом элементов 144 |
| Curved_cantilever_beam_Shell_45.spr | Расчетная модель с типом элементов 45 |
| Curved_cantilever_beam_Shell_145.spr | Расчетная модель с типом элементов 145 |
| Curved_cantilever_beam_Shell_50.spr | Расчетная модель с типом элементов 50 |
| Curved_cantilever_beam_Shell_150.spr | Расчетная модель с типом элементов 150 |
| Curved_cantilever_beam_Solid_36.spr | Расчетная модель с типом элементов 36 |
| Curved_cantilever_beam_Solid_37.spr | Расчетная модель с типом элементов 37 |
Формулировка задачи: Криволинейная изотропная консольная балка прямоугольного поперечного сечения подвергается воздействию на свободном торце сосредоточенных поперечных Py, Pz сил (изгиб в плоскости и из плоскости продольной оси балки). Проверить: точное воспроизведение значений поперечных смещений Y, Z свободного торца криволинейной консольной балки от соответствующих воздействий.
Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
Исходные данные:
| E = 1.0·107 кПа | - модуль упругости материала балки; |
| ν = 0.25 | - коэффициент Пуассона; |
| b = 0. 1 м | - ширина балки; |
| h = 0. 2 м | - высота балки; |
| R = 4.22 м | - радиус дуги продольной оси балки; |
| α = π/2 рад | - центральный угол дуги продольной оси балки; |
| Py = 1.0 кН | - значение поперечной силы, действующей по высоте балки (в плоскости продольной оси); |
| Pz = 1.0 кН | - значение поперечной силы, действующей по ширине балки (из плоскости продольной оси). |
Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема с трапецеидальной сеткой конечных элементов для десяти расчетных моделей:
Модель 1 - 12 трехузловых элементов оболочки типа 42. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 14.
Модель 2 - 12 трехузловых элементов оболочки с учетом сдвига типа 142. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 14.
Модель 3 - 6 четырехузловых элементов оболочки типа 44. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН).. Количество узлов в модели – 14.
Модель 4 - 6 четырехузловых элементов оболочки с учетом сдвига типа 144. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 14.
Модель 5 - 12 шестиузловых элементов оболочки типа 45. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 39.
Модель 6 - 12 шестиузловых элементов оболочки с учетом сдвига типа 145. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 39.
Модель 7 - 6 восьмиузловых элементов оболочки типа 50. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 33.
Модель 8 - 6 восьмиузловых элементов оболочки с учетом сдвига типа 150. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде двух узловых сил (Py = 2∙0.5 кН, Pz = 2∙0.5 кН). Количество узлов в модели – 33.
Модель 9 - 6 восьмиузловых изопараметрических объемных элементов типа 36. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде четырех узловых сил (Py = 4∙0.25 кН, Pz = 4∙0.25 кН). Количество узлов в модели – 28.
Модель 10 - 6 двадцатиузловых изопараметрических объемных элементов типа 37. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанного торца балки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенные поперечные Py, Pz силы представлены в виде четырех узловых сил (Py = 4∙0.25 кН, Pz = 4∙0.25 кН). Количество узлов в модели – 80.
Результаты решения в SCAD
Модели 1 и 2. Расчетная схема
Модели 1 и 2. Деформированная схема


Модель 1. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)


Модель 2. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
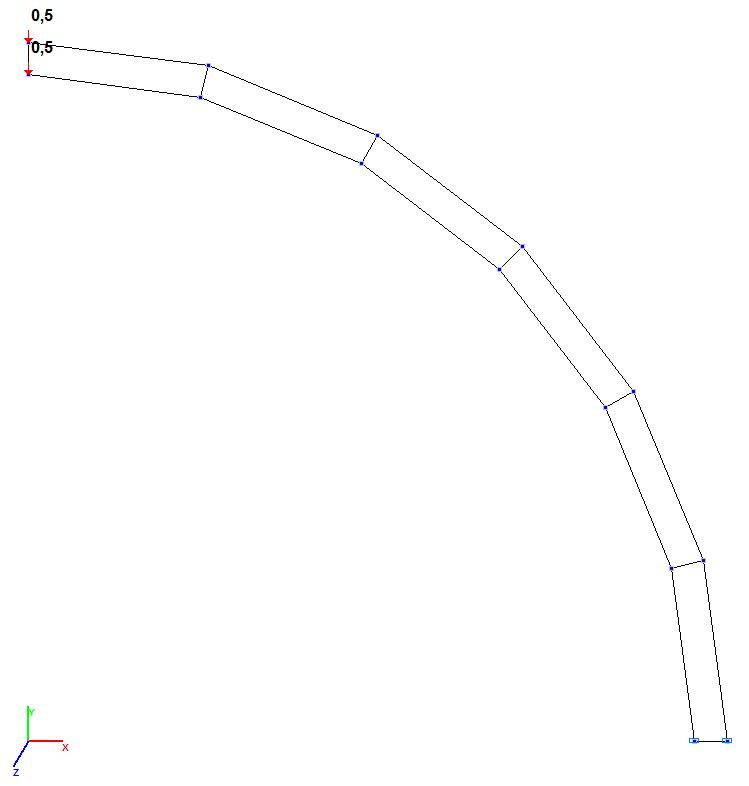
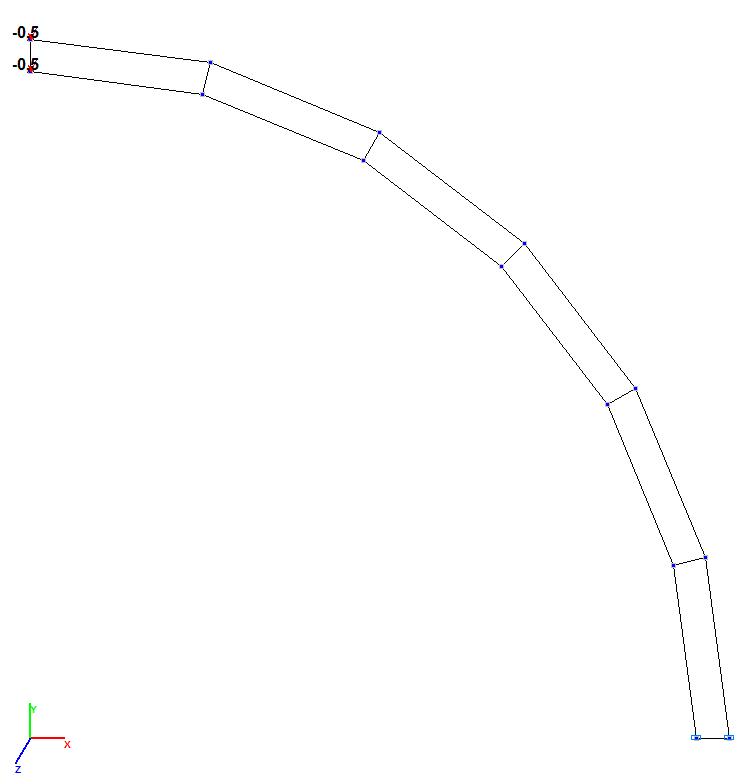
Модели 3 и 4. Расчетная схема
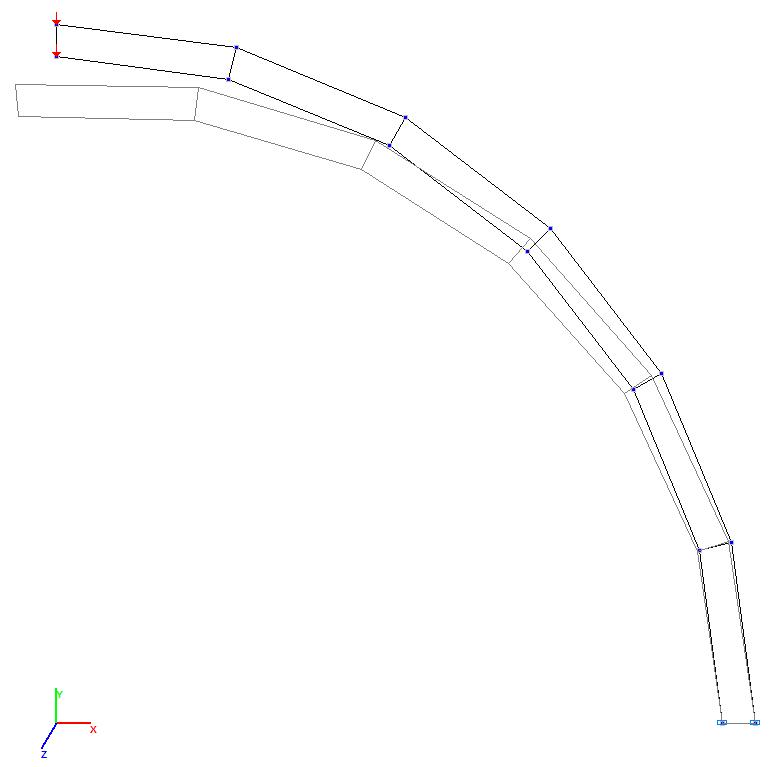
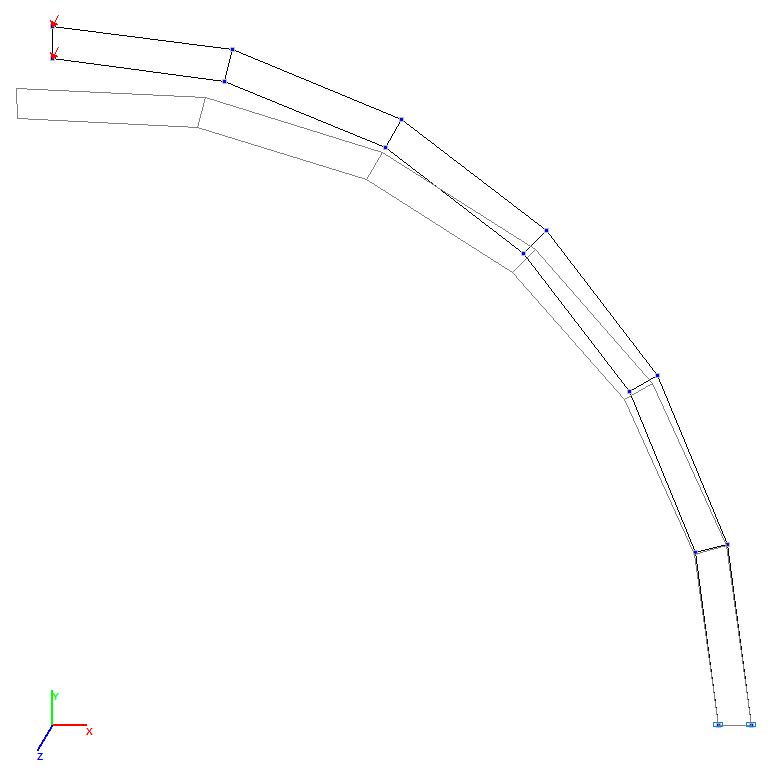
Модели 3 и 4. Деформированная схема
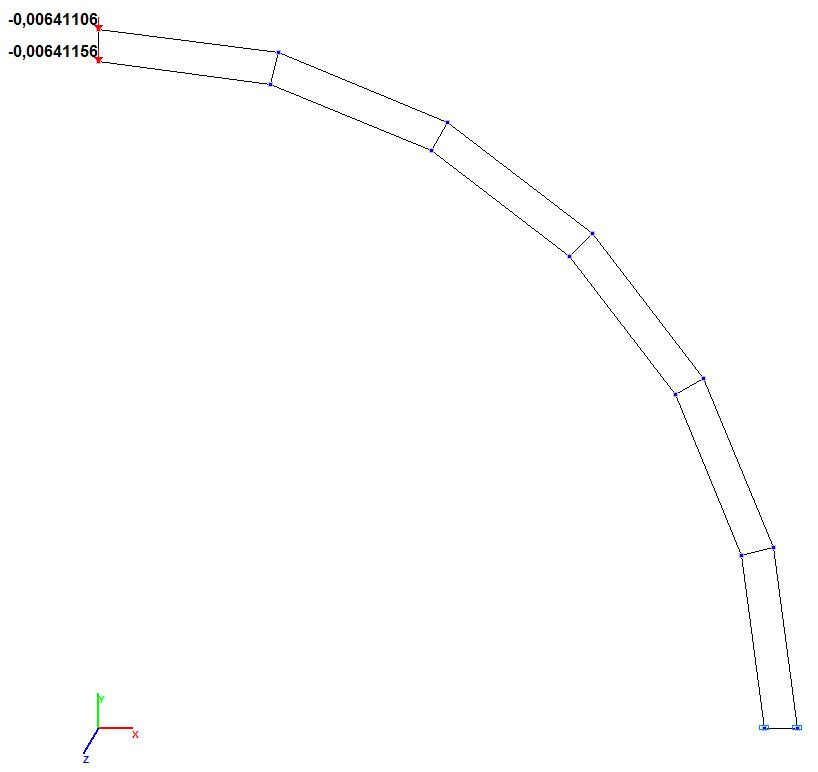
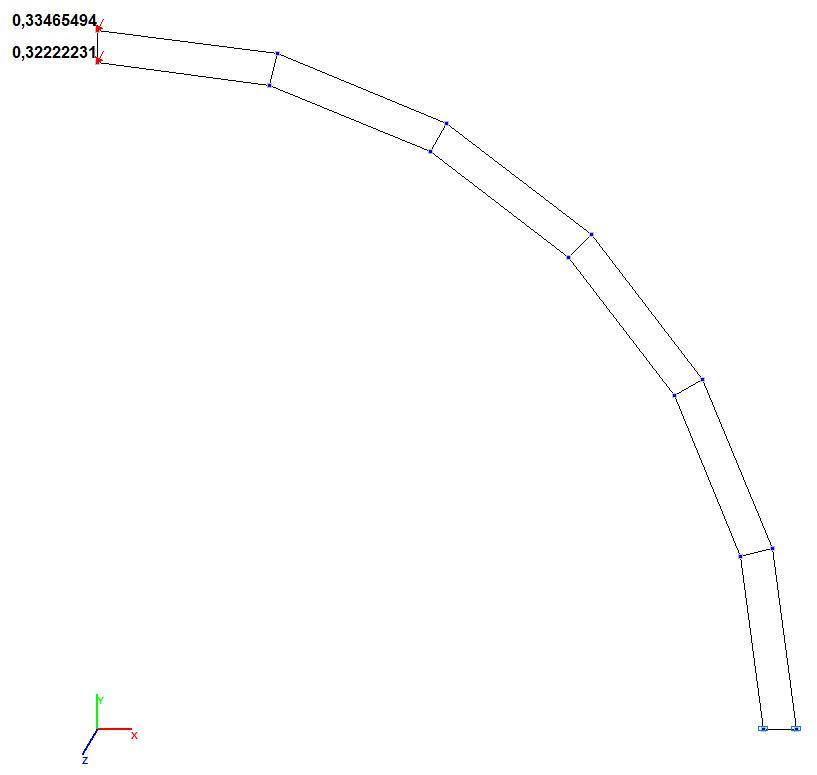
Модель 3. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
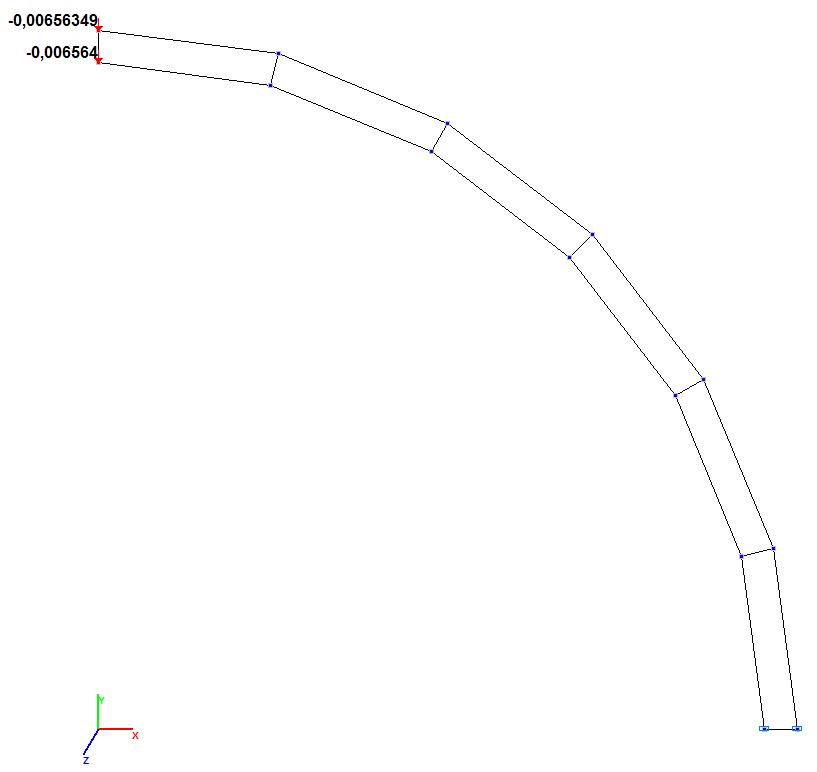
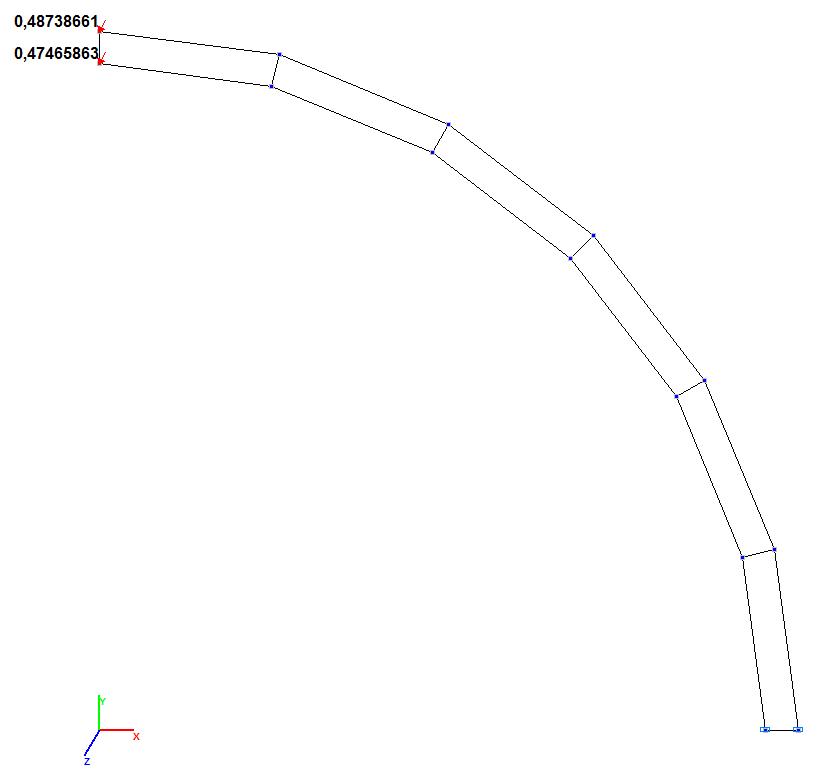
Модель 4. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
Модели 5 и 6. Расчетная схема
Модели 5 и 6. Деформированная схема

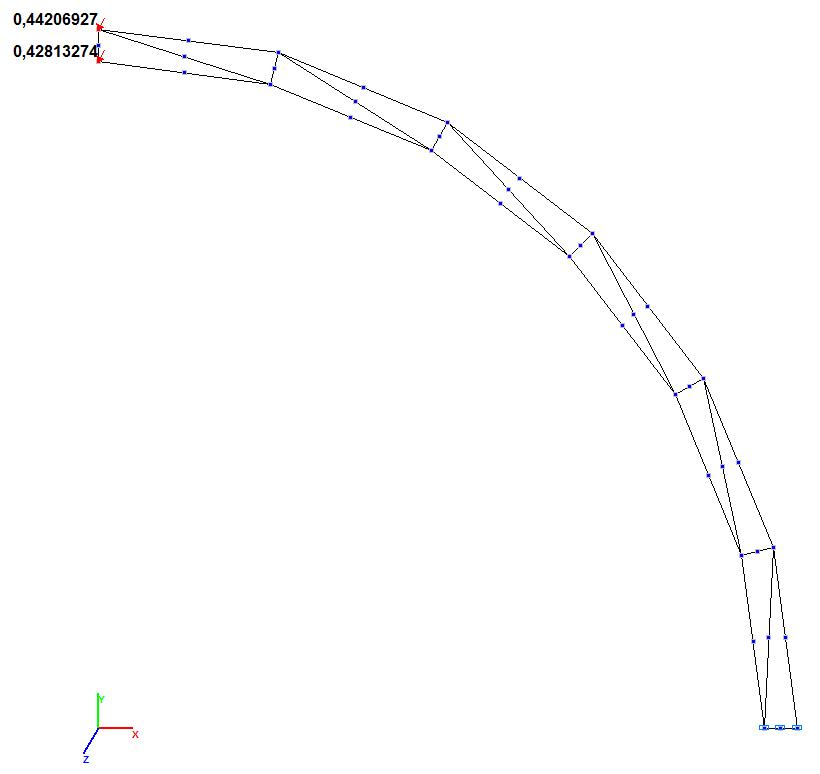
Модель 5. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
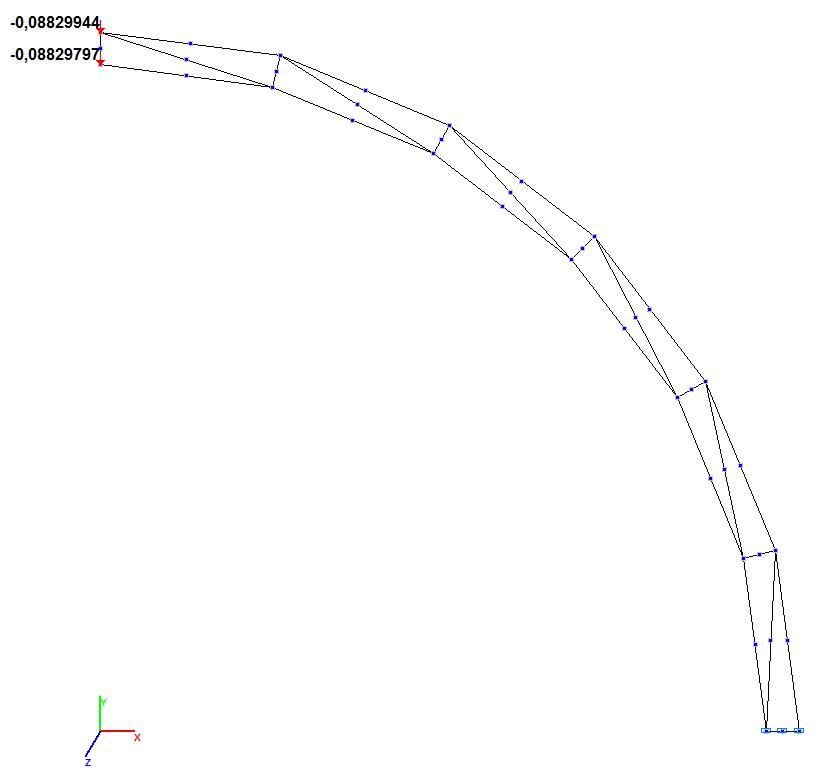

Модель 6. Значения поперечных смещений Y, Z
свободного торца криволинейной консольной балки (м, м)
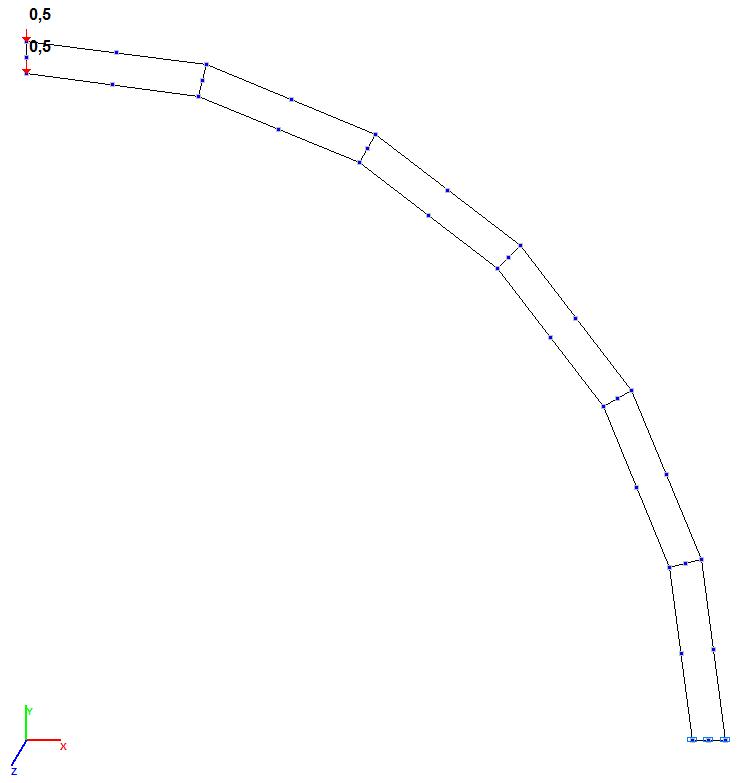
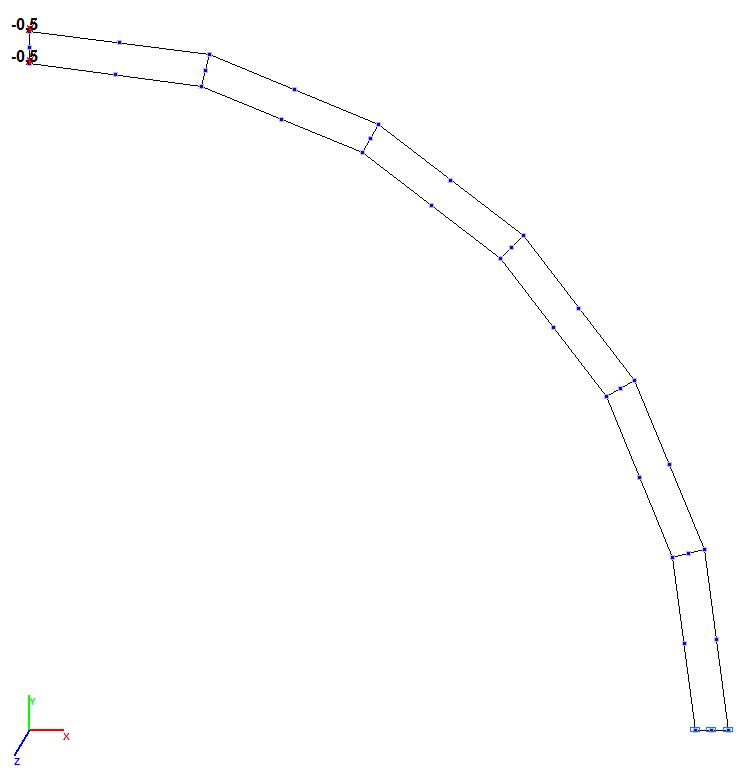
Модели 7 и 8. Расчетная схема
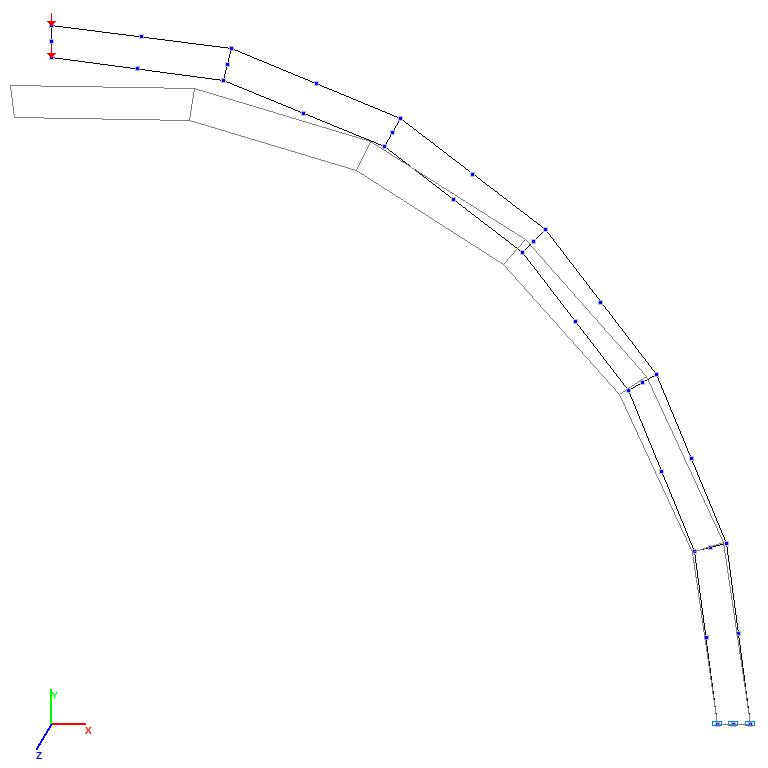
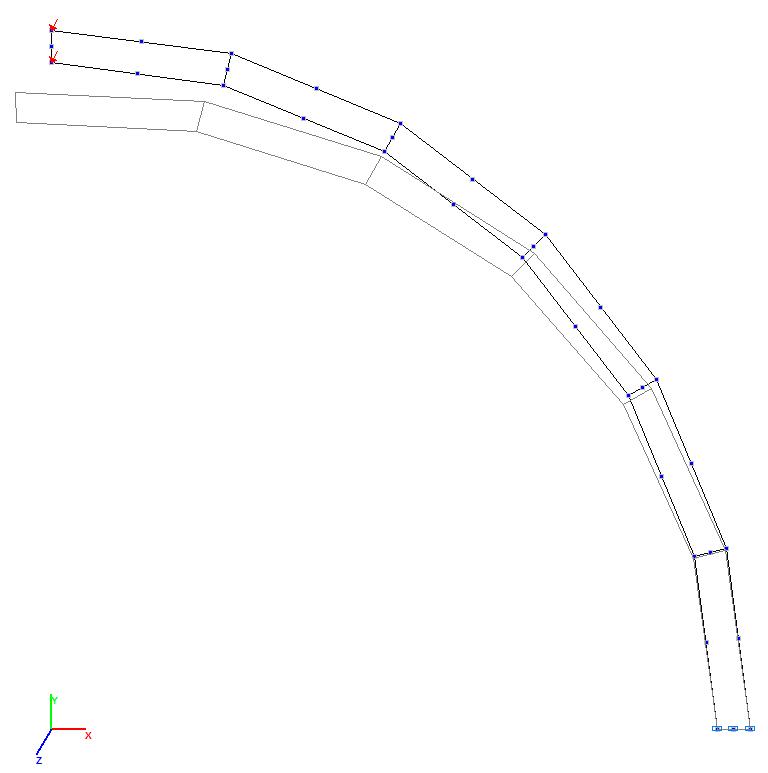
Модели 7 и 8. Деформированная схема

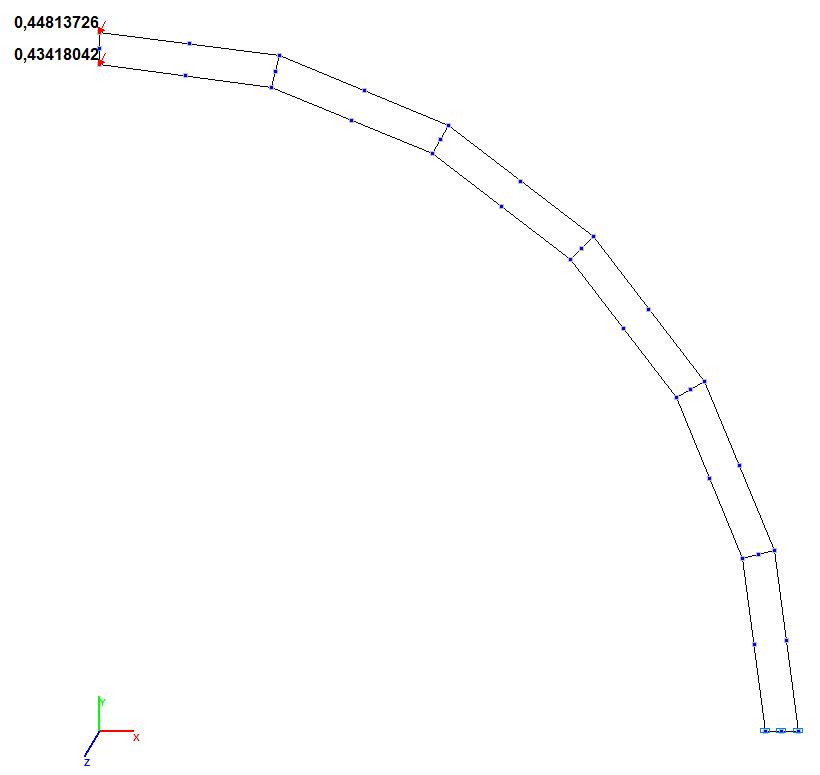
Модель 7. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
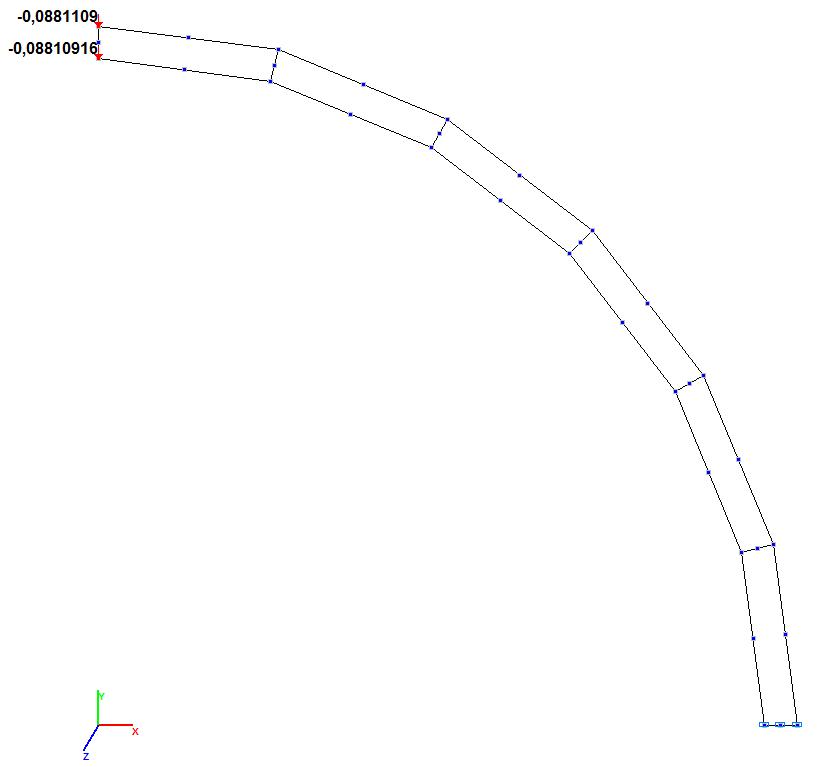
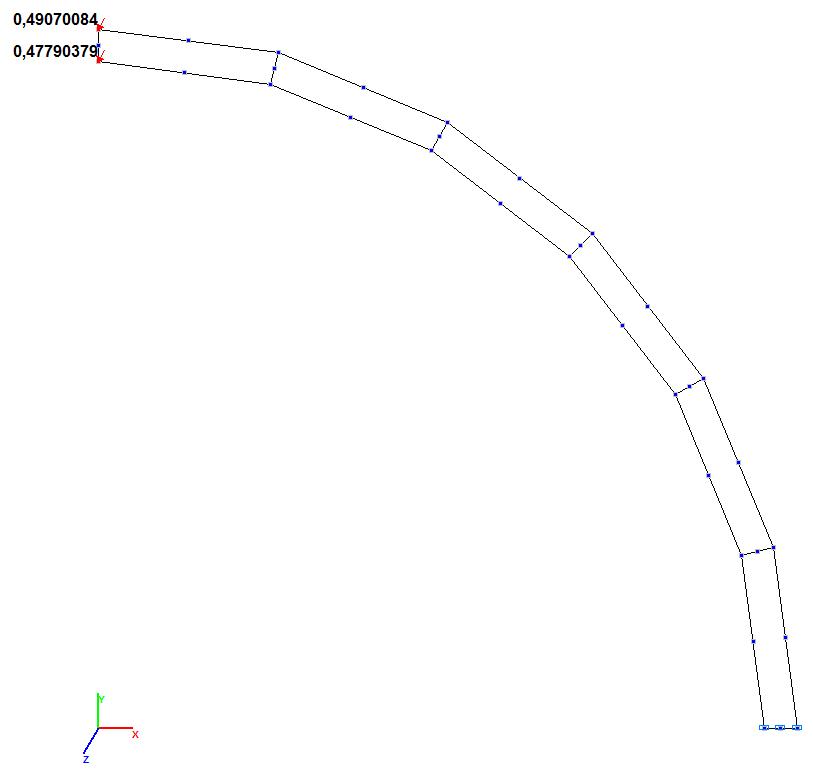
Модель 8. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
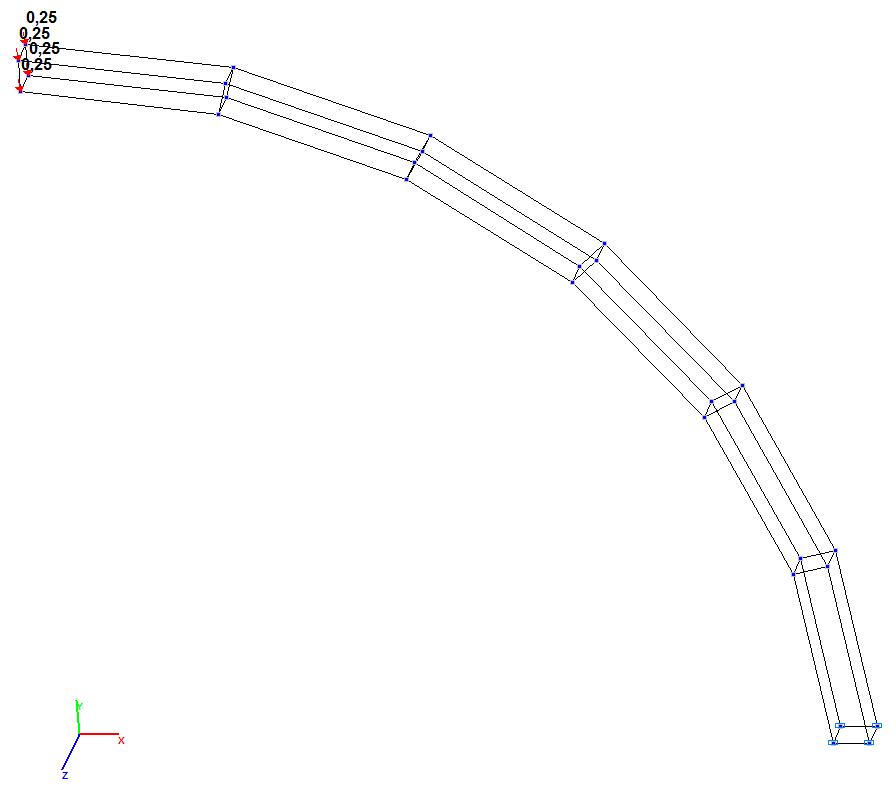
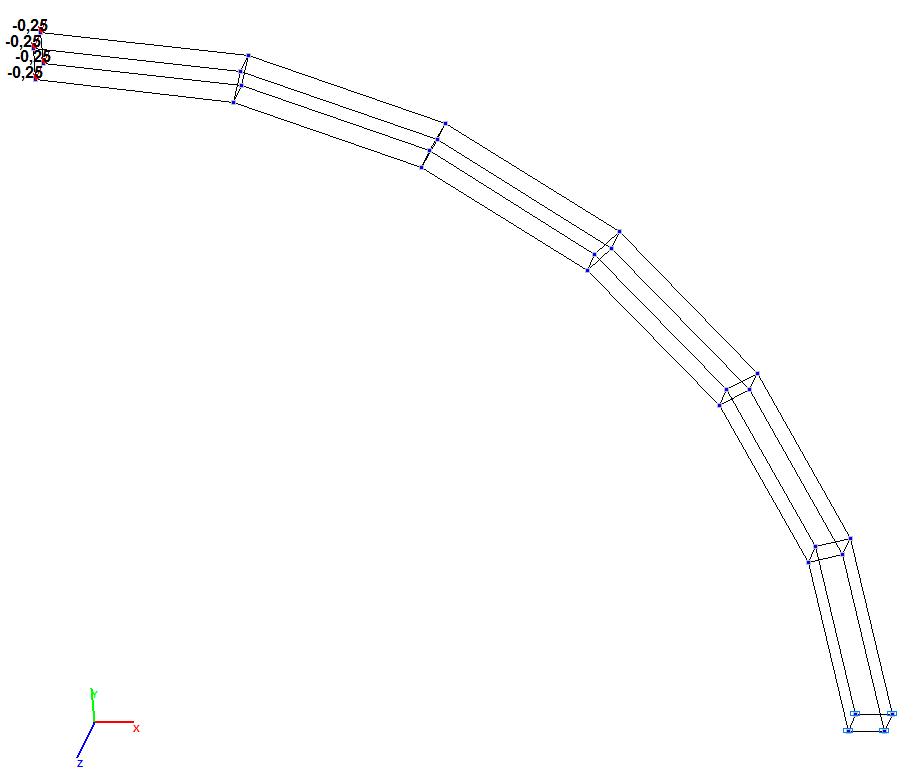
Модель 9. Расчетная схема
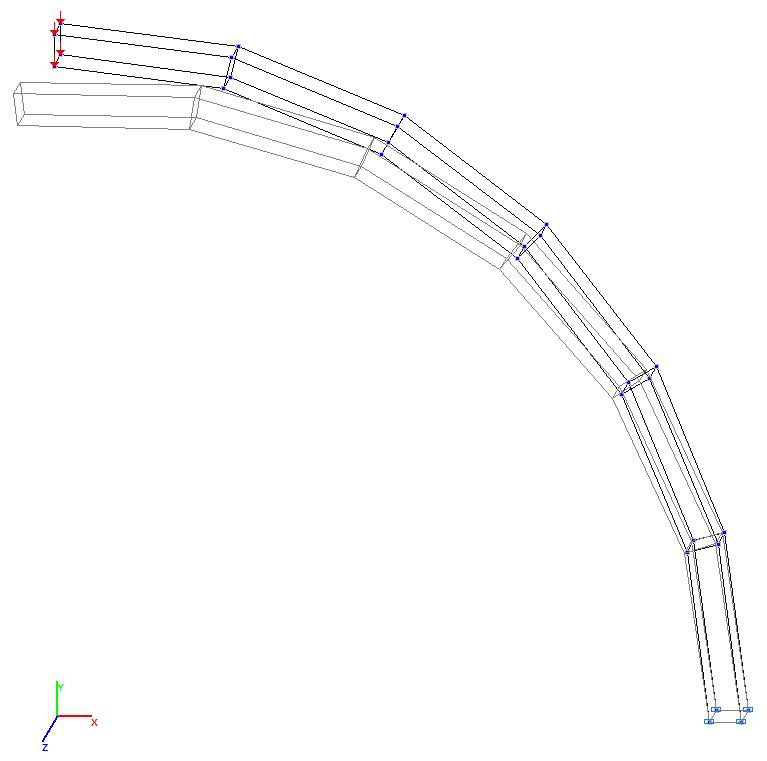
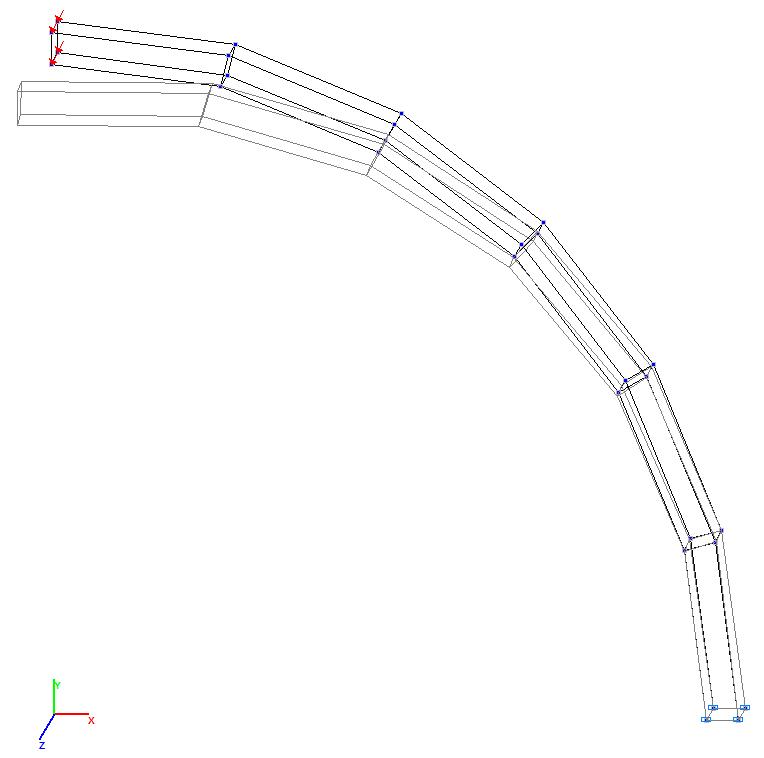
Модель 9. Деформированная схема
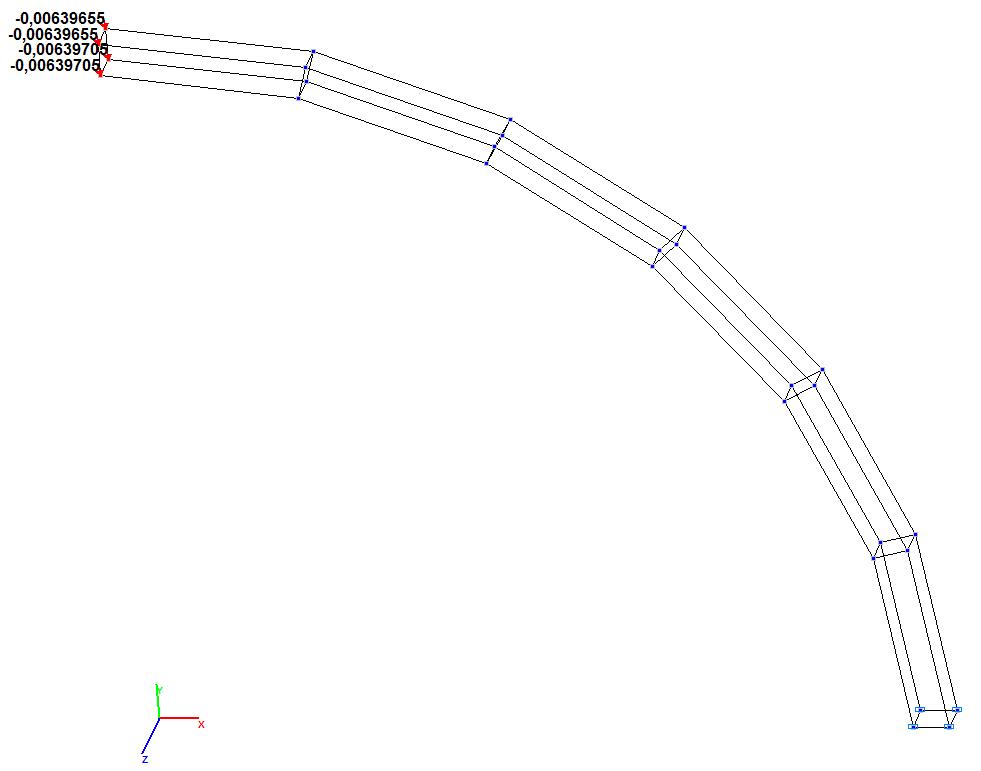
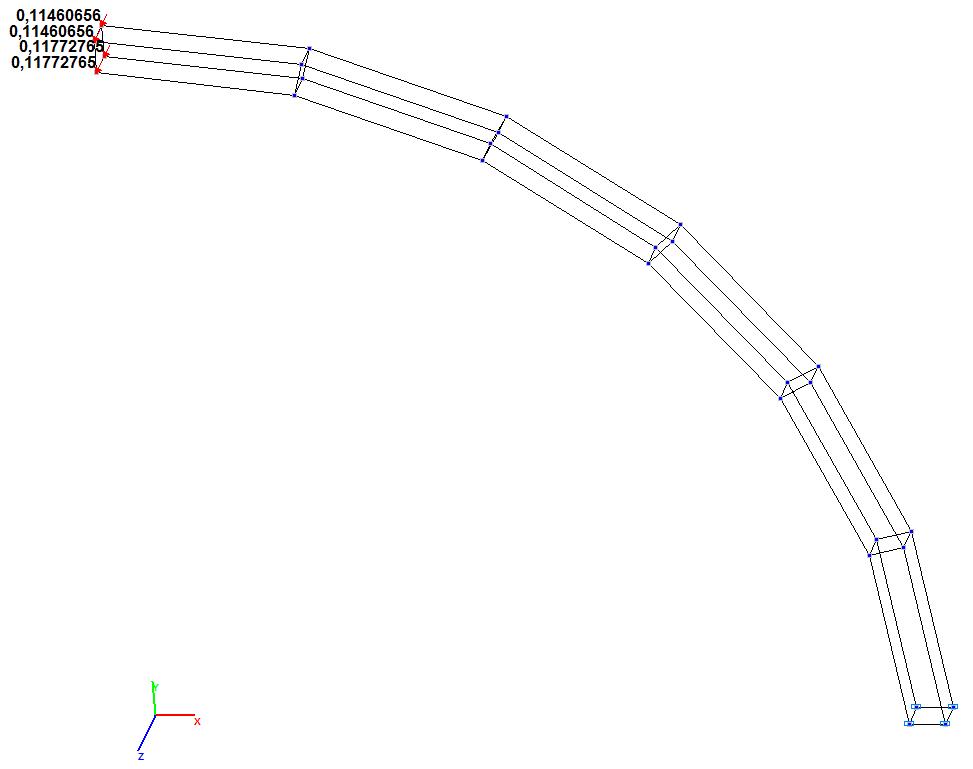
Модель 9. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
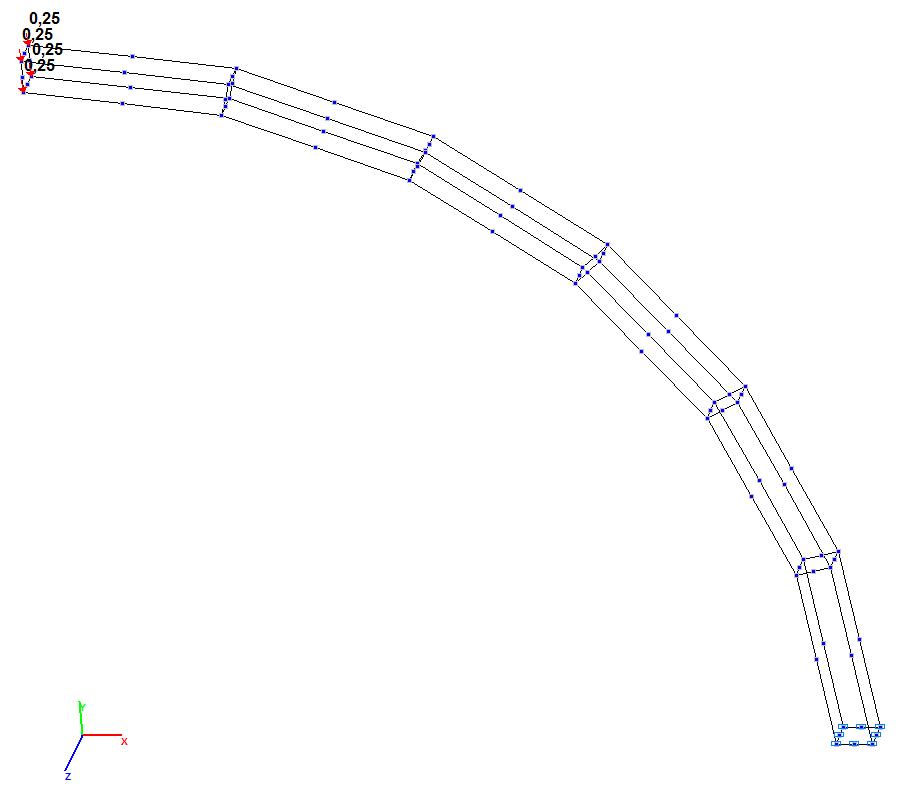
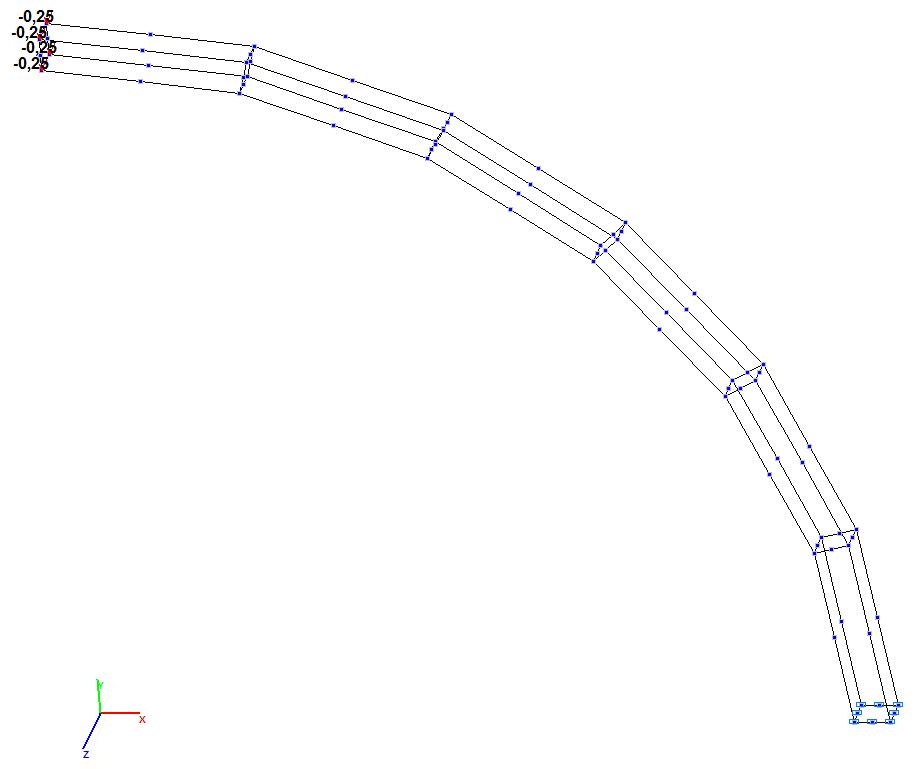
Модель 10. Расчетная схема
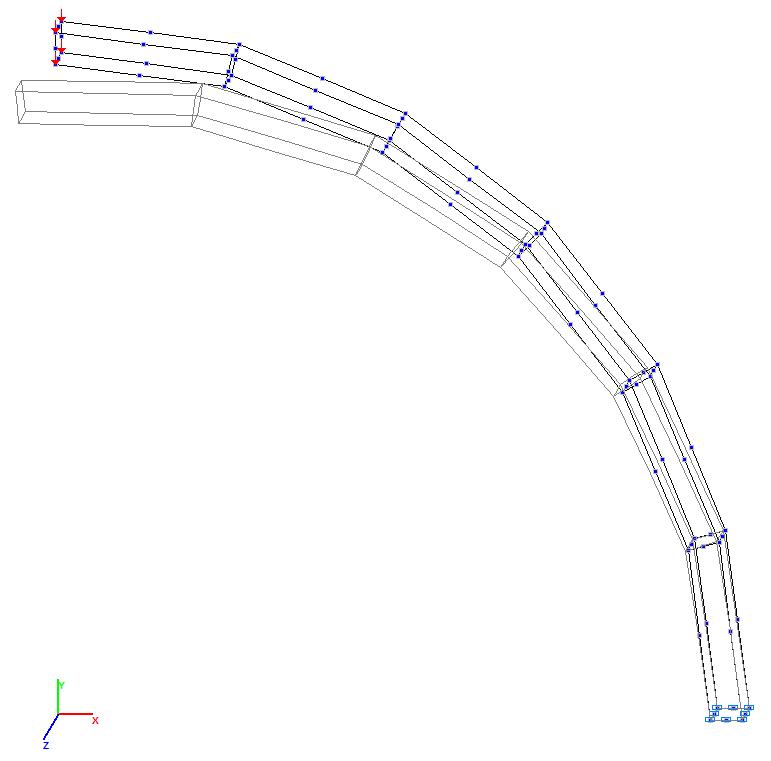
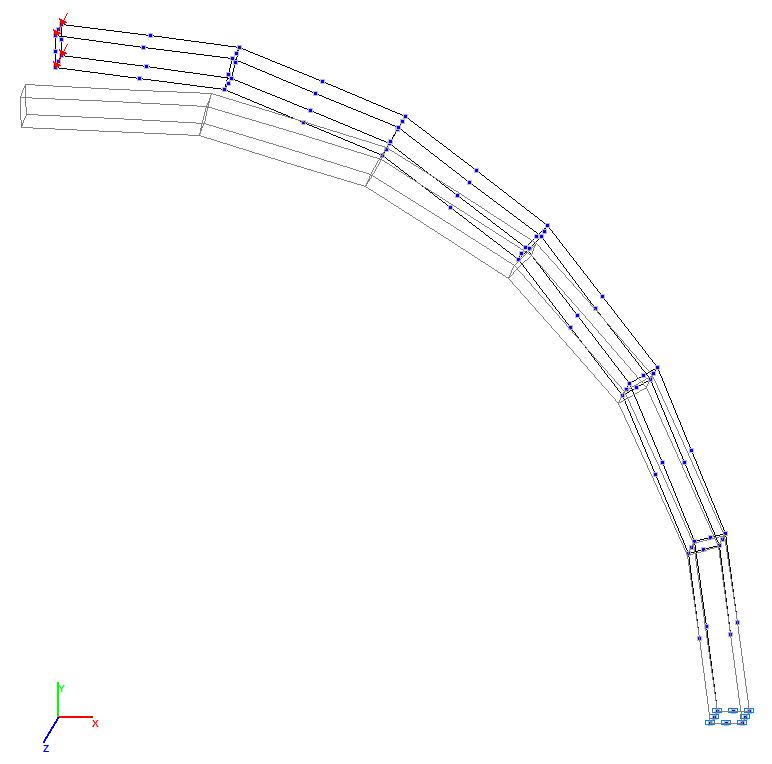
Модель 10. Деформированная схема
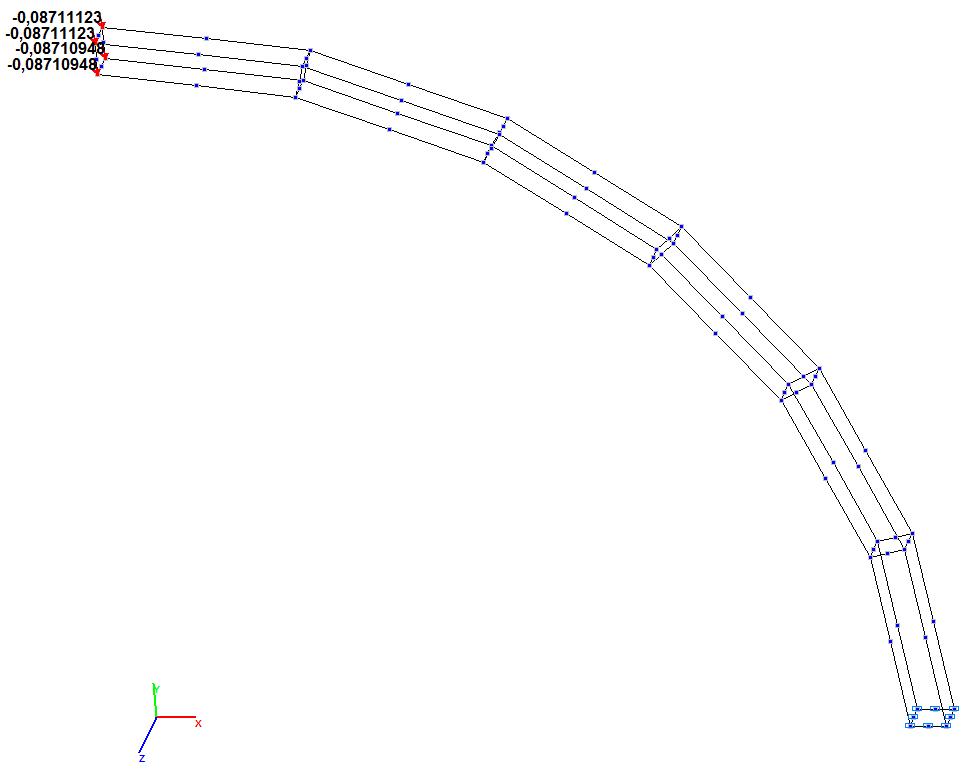
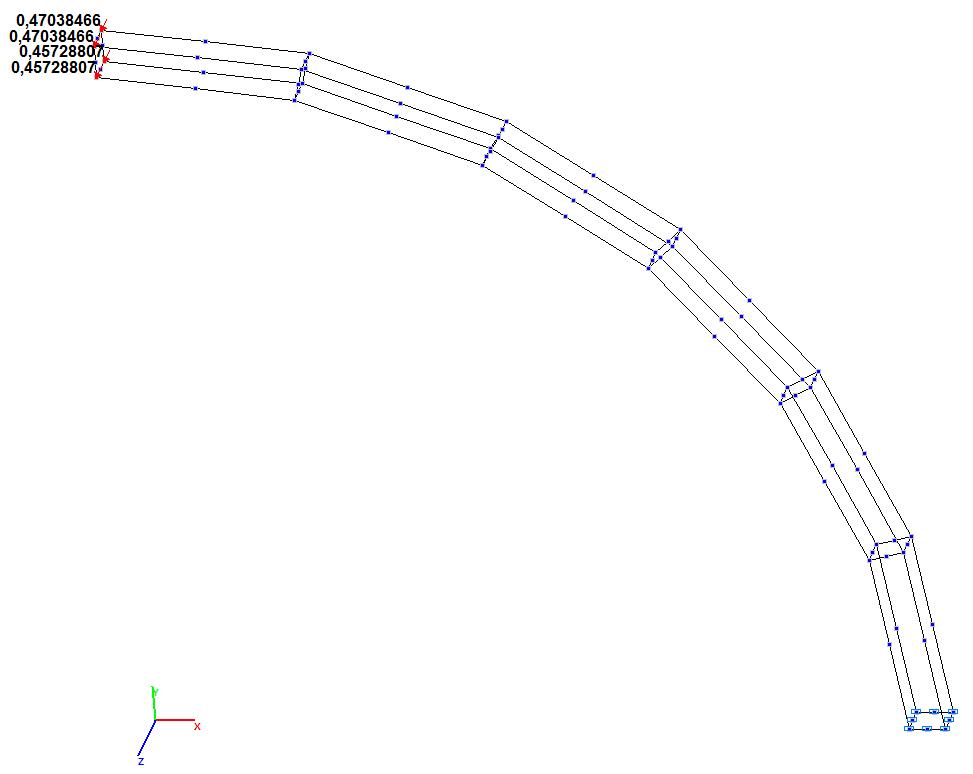
Модель 10. Значения поперечных смещений Y, Z свободного торца криволинейной консольной балки (м, м)
Сравнение решений:
|
Модель |
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.002213 |
97.50 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.454527* |
0.308152 |
32.20 |
|
|
2 (Тип элемента142) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.02213 |
97.50 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.474844 |
5.12 |
|
|
3 (Тип элемента44) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.006411 |
92.76 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.454527* |
0.334655 |
26.37 |
|
|
4 (Тип элемента144) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.006563 |
92.59 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.487387 |
2.61 |
|
|
5 (Тип элемента45) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.088299 |
0.27 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.454527* |
0.442069 |
2.74 |
|
|
6 (Тип элемента145) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.088299 |
0.27 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.487623 |
2.57 |
|
|
7 (Тип элемента50) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.088111 |
0.48 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.454527* |
0.448137 |
1.41 |
|
|
8 (Тип элемента150) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.088111 |
0.48 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.490701 |
1.95 |
|
|
9 (Тип элемента36) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.006397 |
92.77 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.114607 |
77.10 |
|
|
10 (Тип элемента37) |
Поперечное смещение Y свободного торца консольной балки, м |
0.088536 |
0.087111 |
1.61 |
|
Поперечное смещение Z свободного торца консольной балки, м |
0.500466 |
0.470384 |
6.01 |
* Значения поперечных смещений Z для тонких пластин (без учета сдвига) определены при моменте инерции свободного кручения, вычисленном с величиной коэффициента kf, равной 1/3 (h/b = ∞).
Замечания: При аналитическом решении значения поперечных смещений Y, Z свободного торца криволинейной консольной балки от соответствующих воздействий определяются по следующим формулам:
\[ Y=\frac{3\cdot \pi \cdot P_{y} \cdot R^{3}}{E\cdot b\cdot h^{3}}; \quad Z=\frac{P_{z} \cdot R^{3}}{2\cdot E\cdot b^{3}\cdot h\cdot k_{f} }\cdot \left[ {6\cdot \pi \cdot k_{f} +\left( {3\cdot \pi -8} \right)\cdot \left( {1+\nu } \right)} \right], \] \[ где: \quad k_{f} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{b}{h}\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\}. \]
