Свободно опертая плоская прямоугольная пластина под действием равномерно распределенной по всей площади поперечной нагрузки и сосредоточенной поперечной силы в центре
Цель: Проверка точного воспроизведения значений поперечных перемещений в центре свободно опертой плоской прямоугольной пластины от действия равномерно распределенной по всей площади поперечной нагрузки и сосредоточенной поперечной силы в центре.
Файлы с исходными данными:
| Расчетная модель с типом элементов 42 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 44 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 45 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 50 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 36 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 | |
| Расчетная модель с типом элементов 37 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 |
Формулировка задачи: Свободно опертая плоская прямоугольная пластина подвергается воздействию равномерно распределенной по всей площади поперечной нагрузки q и сосредоточенной поперечной силы в центре P. Проверить: точное воспроизведение значений поперечных перемещений в центре свободно опертой плоской прямоугольной пластины wq и wP от соответствующих воздействий.
Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
S. Timoshenko, S. Woinowsky-Krieger, Theory of plates and shells, New York, McGraw-Hill,1959, p. 120, 143, 202, 206.
Исходные данные:
| E = 1.7472·107 кПа | - модуль упругости материала пластины; |
| ν = 0.30 | - коэффициент Пуассона; |
| a = 2.00 м | - ширина пластины; |
| b = 10.00 м | - длина пластины; |
| h = 10-4 (10-2) м | - толщина пластины; |
| q = 1.0·10-4 кН/м2 | - значение равномерно распределенной по всей площади пластины поперечной нагрузки; |
| P = 4.0·10-4 кН | - значение сосредоточенной поперечной силы в центре пластины. |
Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема четверти пластины по условиям симметрии для шести расчетных моделей:
Модель 1 – 8, 32, 128 трехузловых элементов оболочки типа 42 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 2 – 4, 16, 64 четырехузловых элемента оболочки типа 44 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 3 – 8, 32, 128 шестиузловых элементов оболочки типа 45 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 4 – 4, 16, 64 восьмиузловых элемента оболочки типа 50 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных кромок пластины по направлениям степеней свободы X, Y, Z, UX, UY, UZ и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 5 – 4, 16, 64, 256, 1024, 4096, 16384 восьмиузловых изопараметрических объемных элемента типа 36 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Толщина пластины – 10-2 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных ребер нижней поверхности пластины по направлениям степеней свободы X, Y, Z, на узлы заделанных ребер верхней поверхности пластины, параллельных оси Y общей системы координат, по направлению степени свободы X, на узлы заделанных ребер верхней поверхности пластины, параллельных оси X общей системы координат, по направлению степени свободы Y и связей по условиям симметрии. Количество узлов в модели – 18, 50, 162, 578, 2178, 8450, 33282.
Модель 6 – 4, 16, 64, 256, 1024, 4096, 16384 двадцатиузловых изопараметрических объемных элемента типа 37 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Толщина пластины – 10-2 м. Обеспечение граничных условий достигается за счет наложения связей на узлы заделанных ребер нижней поверхности пластины по направлениям степеней свободы X, Y, Z, на узлы заделанных ребер верхней поверхности пластины, параллельных оси Y общей системы координат, по направлению степени свободы X, на узлы заделанных ребер верхней поверхности пластины, параллельных оси X общей системы координат, по направлению степени свободы Y и связей по условиям симметрии. Количество узлов в модели – 51, 155, 531, 1955, 7491, 29315, 115971.
Результаты решения в SCAD
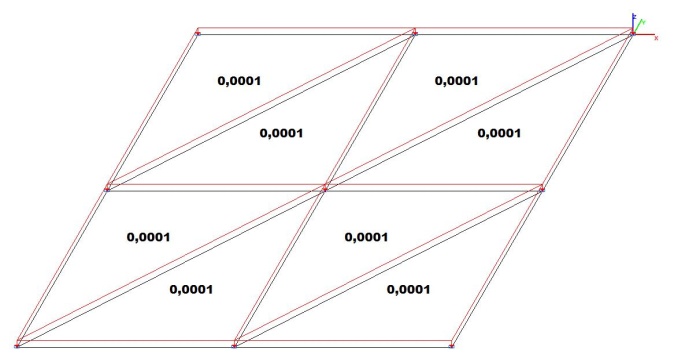
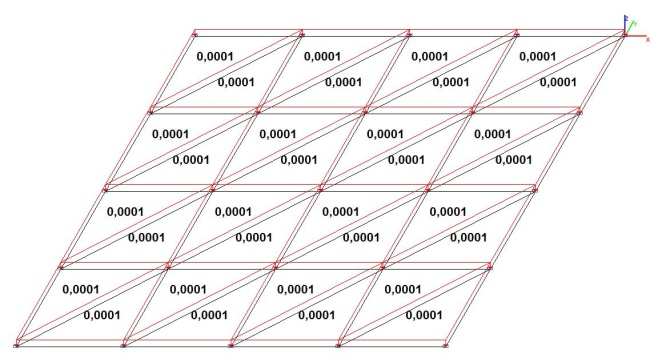
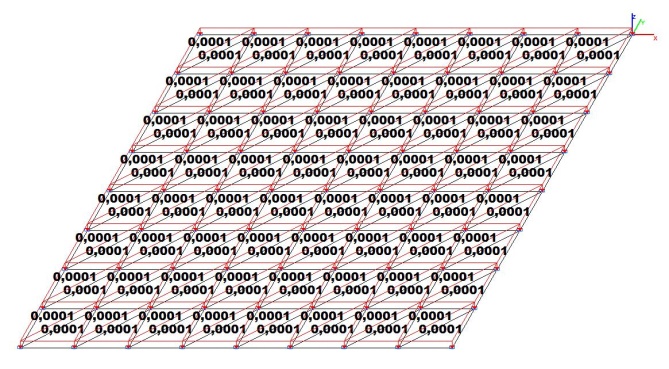
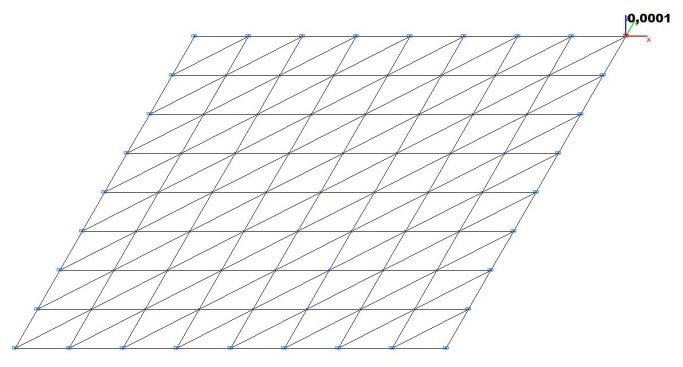
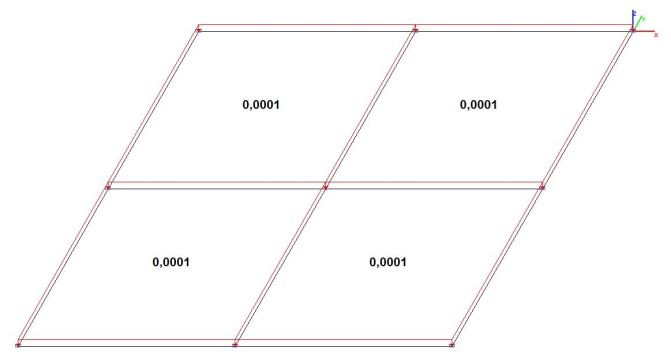
Модель 1. Расчетная схема
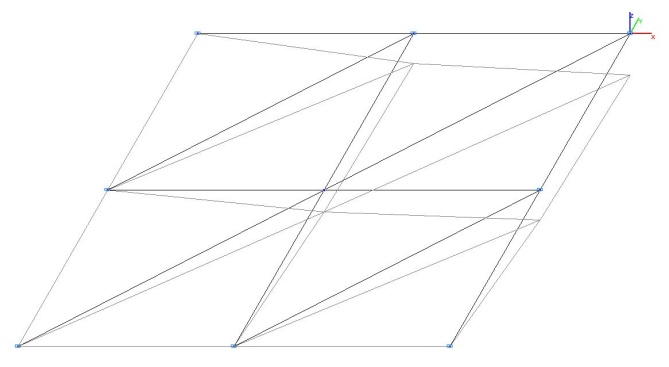
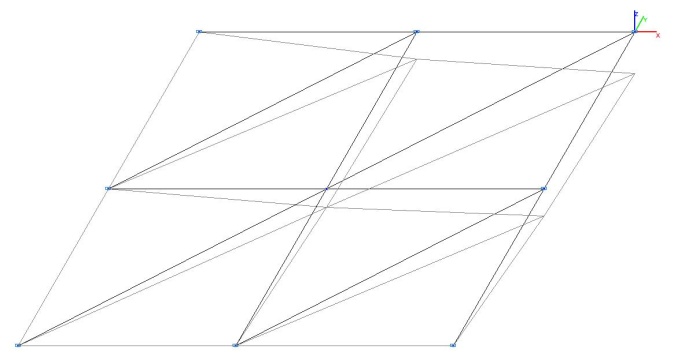
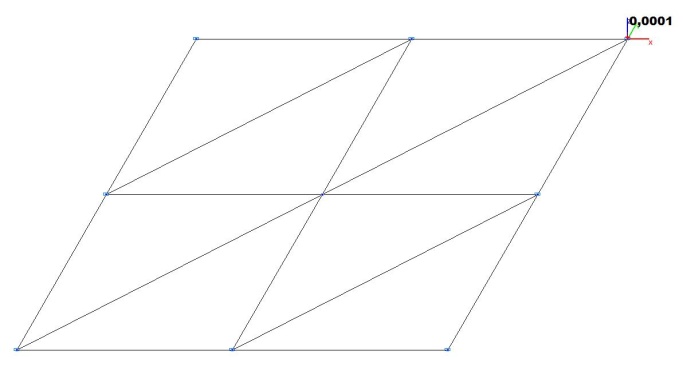
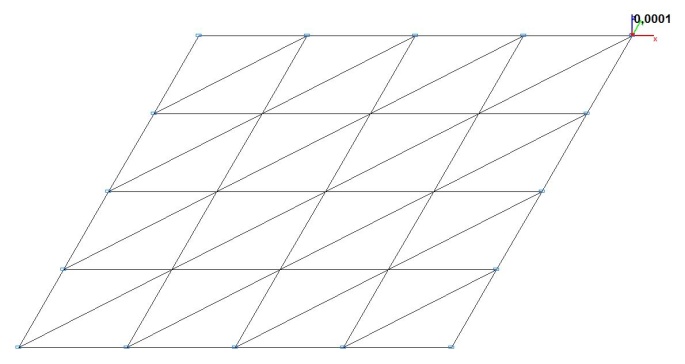
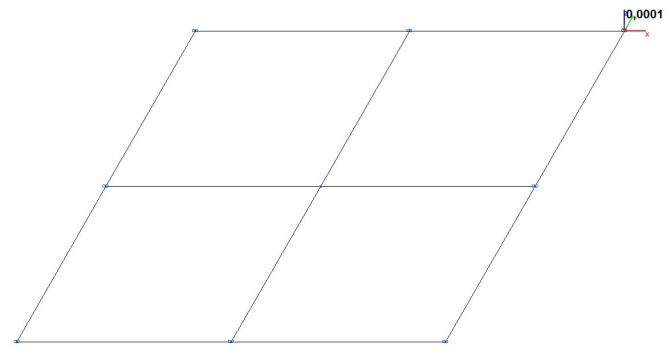
Модель 1. Деформированная схема






Модель 1. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
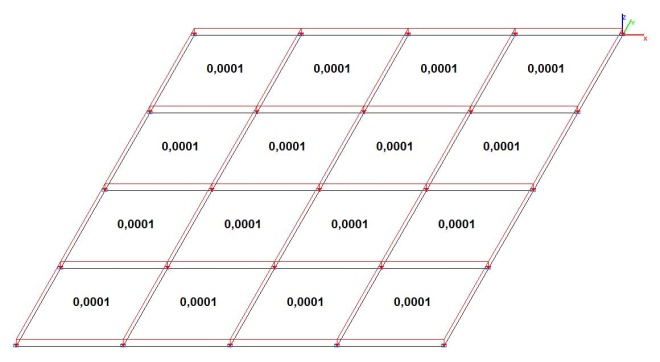
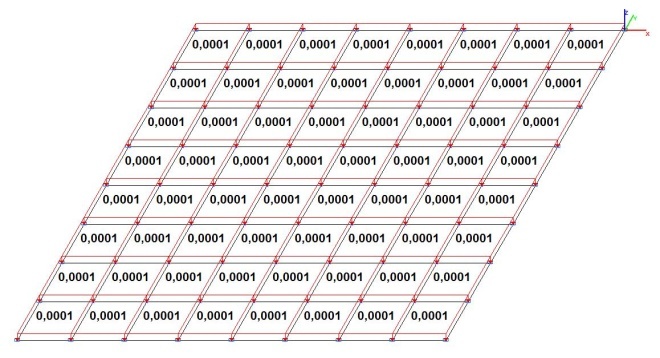
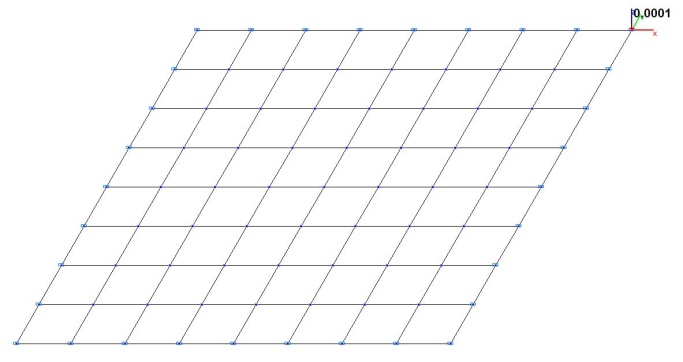
Модель 2. Расчетная схема
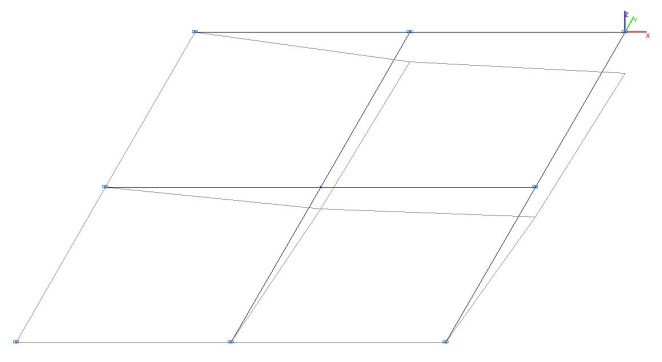
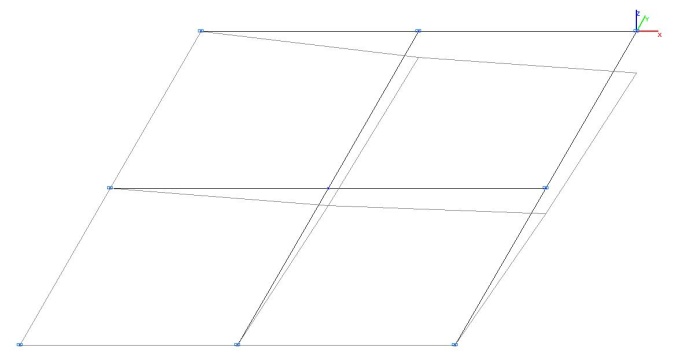
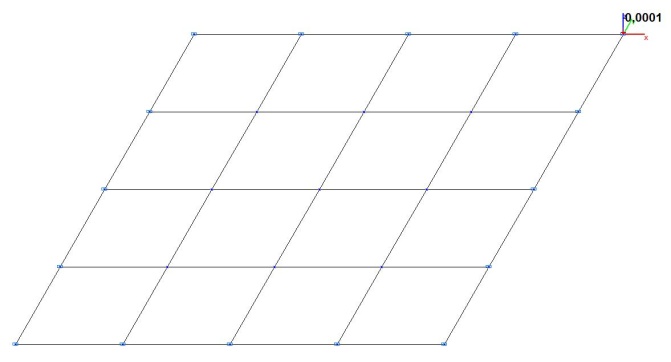
Модель 2. Деформированная схема


Модель 2. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
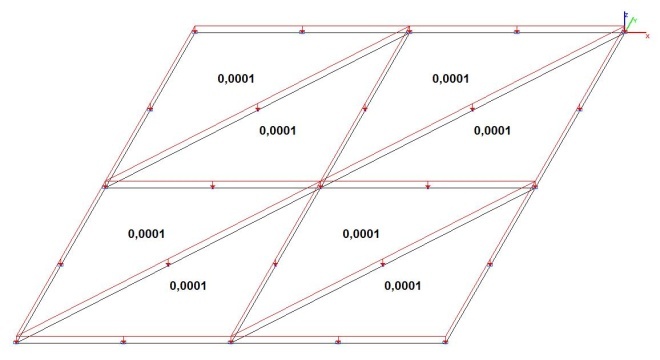
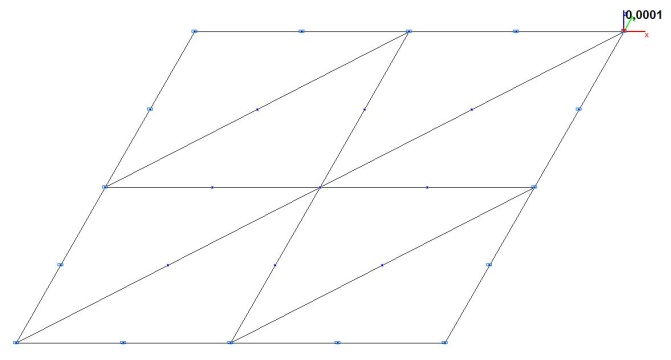
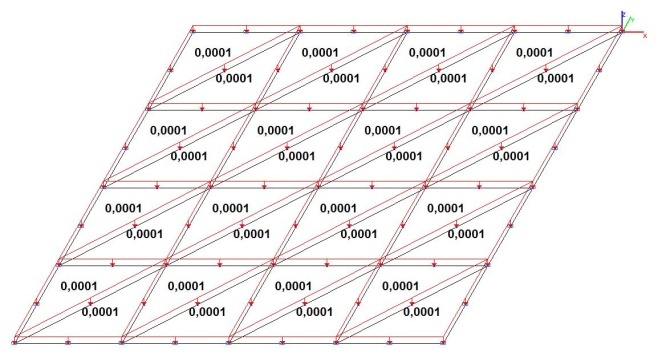
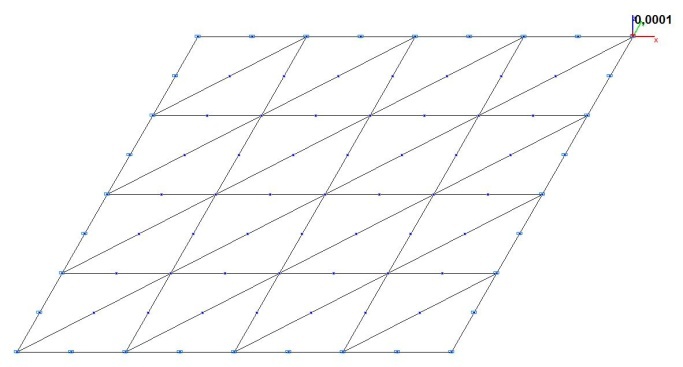
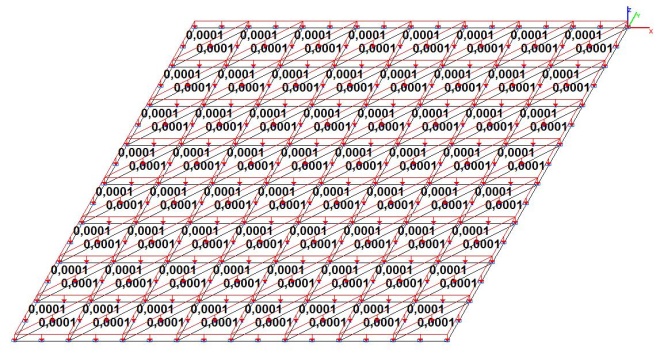
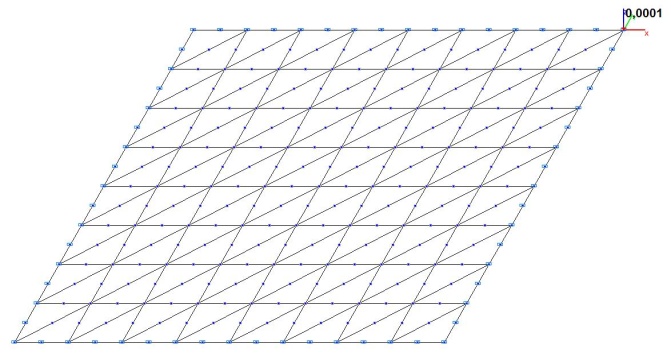
Модель 3. Расчетная схема
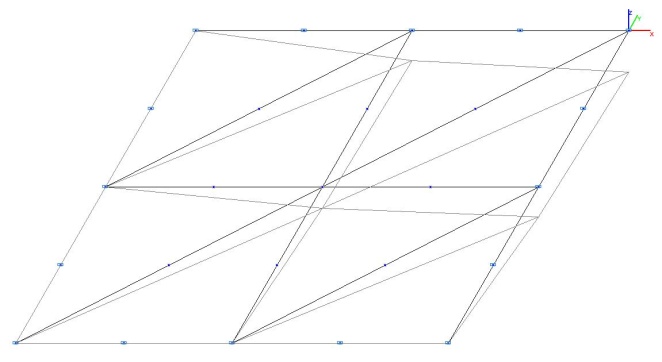
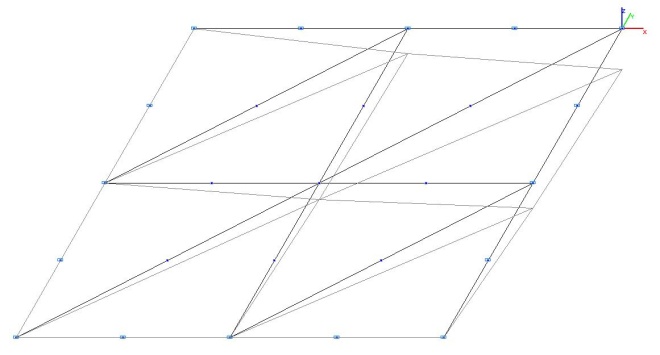

Модель 3. Деформированная схема






Модель 3. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
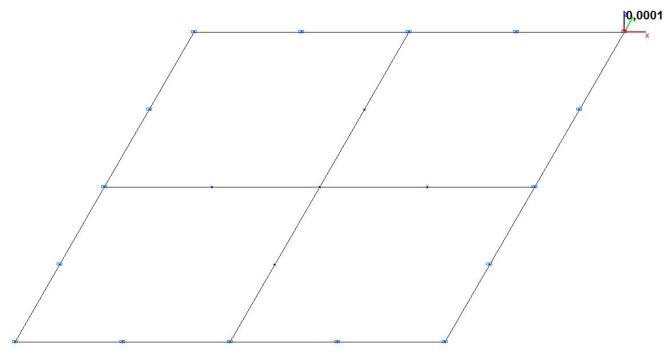
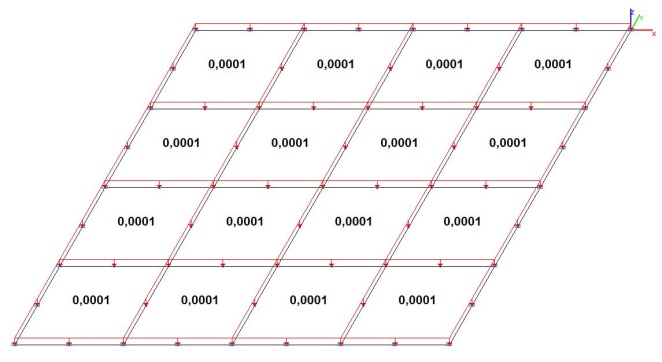
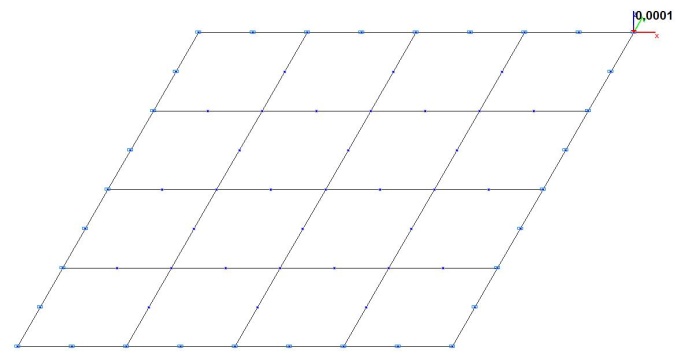

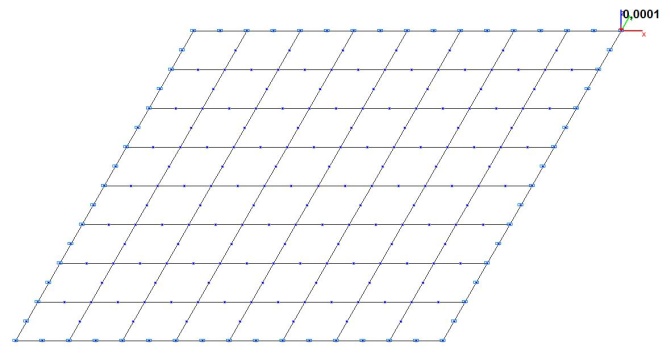
Модель 4. Расчетная схема
Модель 4. Деформированная схема

Модель 4. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
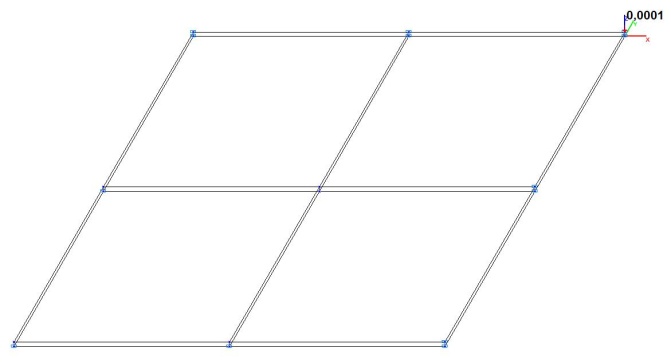
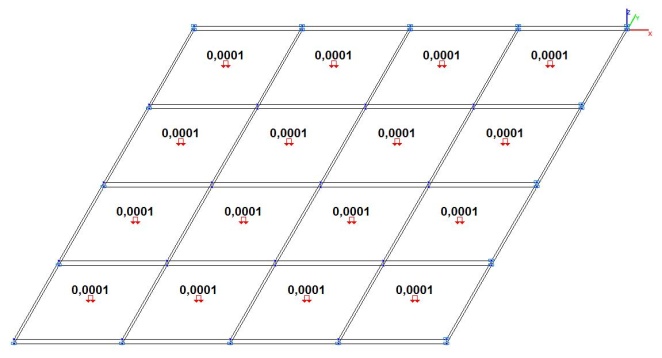
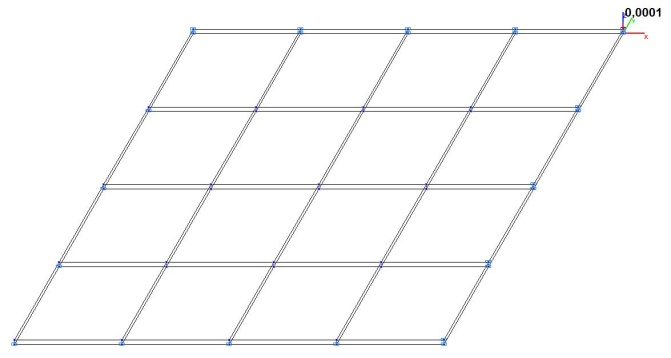
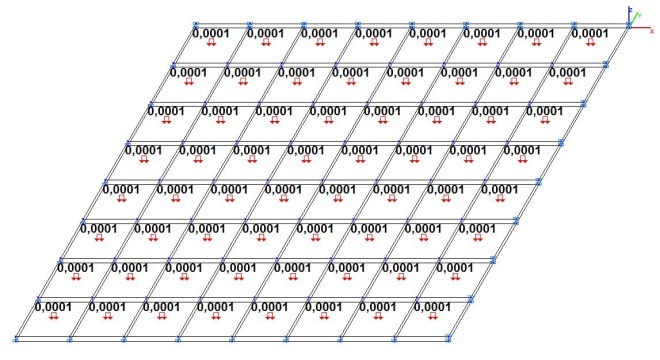
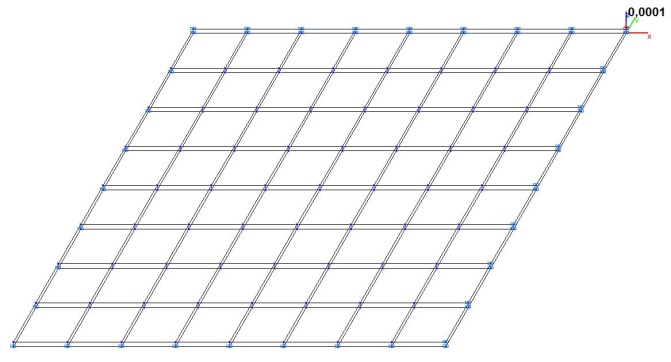
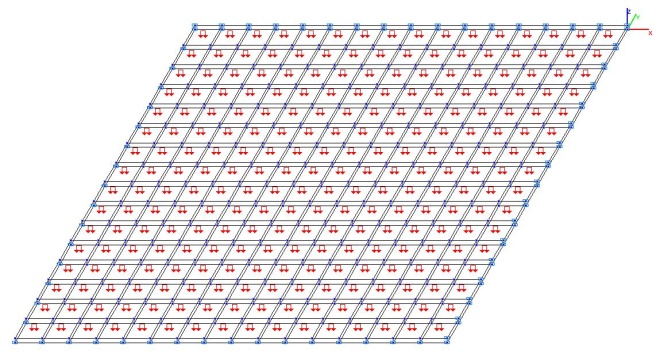
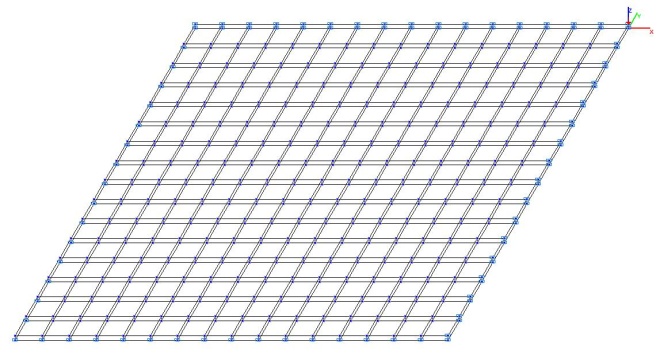
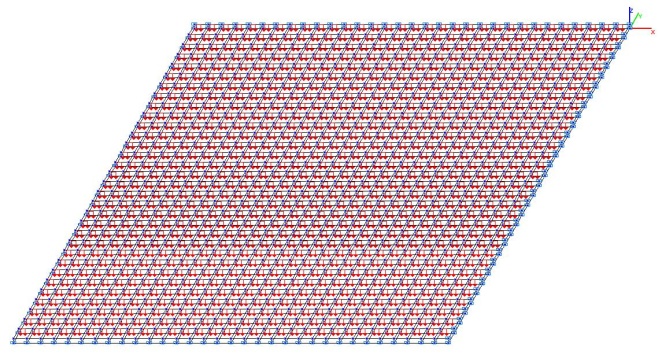





Модель 5. Расчетная схема




Модель 5. Деформированная схема










Модель 5. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
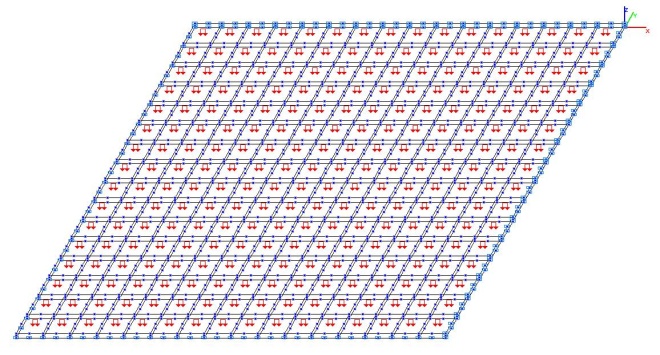
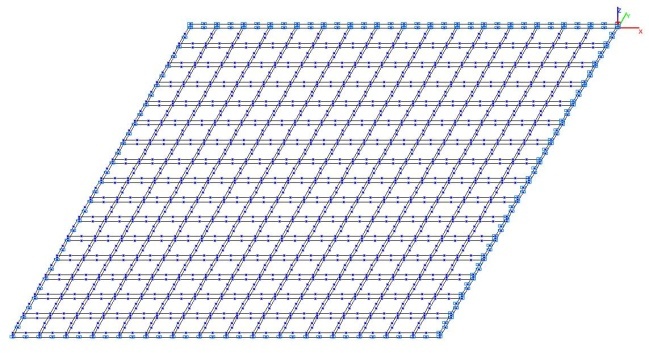
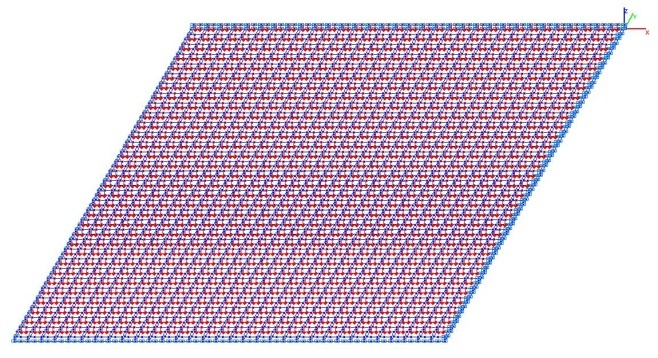





Модель 6. Расчетная схема
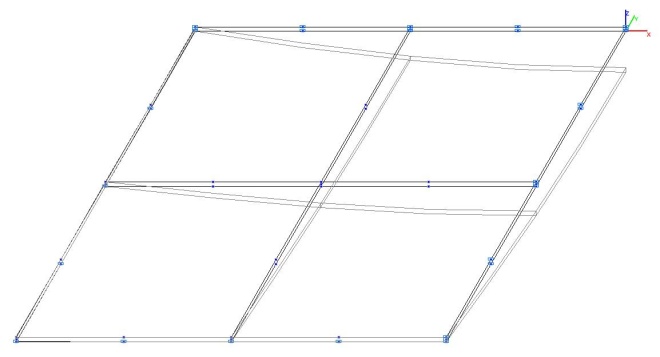





Модель 6. Деформированная схема








Модель 6. Значения поперечных перемещений в центре свободно опертой прямоугольной пластины wq и wP (м, м)
Сравнение решений:
Поперечные перемещения в центре свободно опертой плоской прямоугольной пластины wq от воздействия равномерно распределенной по всей площади поперечной нагрузки q
|
Модель |
Сетка конечных элементов |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
2x2 |
12.971 |
11.804 |
9.00 |
|
4x4 |
12.847 |
0.96 |
||
|
8x8 |
12.958 |
0.10 |
||
|
2 (Тип элемента 44) |
2x2 |
12.971 |
12.528 |
3.42 |
|
4x4 |
13.093 |
0.94 |
||
|
8x8 |
13.030 |
0.45 |
||
|
3 (Тип элемента 45) |
2x2 |
12.971 |
13.029 |
0.45 |
|
4x4 |
12.973 |
0.02 |
||
|
8x8 |
12.971 |
0.00 |
||
|
4 (Тип элемента 50) |
2x2 |
12.971 |
13.020 |
0.38 |
|
4x4 |
12.971 |
0.00 |
||
|
8x8 |
12.971 |
0.00 |
||
|
5 (Тип элемента 36) |
2x2 |
12.971∙10-6 |
0.017∙10-6 |
99.87 |
|
4x4 |
0.067∙10-6 |
99.48 |
||
|
8x8 |
0.264∙10-6 |
97.96 |
||
|
16x16 |
0.983∙10-6 |
92.42 |
||
|
32x32 |
3.099∙10-6 |
76.11 |
||
|
64x64 |
6.656∙10-6 |
48.69 |
||
|
128x128 |
9.234∙10-6 |
28.81 |
||
|
6 (Тип элемента 37) |
2x2 |
12.971∙10-6 |
9.000∙10-6 |
30.61 |
|
4x4 |
13.308∙10-6 |
2.60 |
||
|
8x8 |
12.931∙10-6 |
0.31 |
||
|
16x16 |
12.963∙10-6 |
0.06 |
||
|
32x32 |
12.971∙10-6 |
0.00 |
||
|
64x64 |
12.972∙10-6 |
0.01 |
||
|
128x128 |
12.973∙10-6 |
0.02 |
Поперечные перемещения в центре свободно опертой плоской прямоугольной пластины wP от воздействия сосредоточенной поперечной силы в центре P
|
Модель |
Сетка конечных элементов |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
2x2 |
16.960 |
7.771 |
54.18 |
|
4x4 |
11.983 |
29.34 |
||
|
8x8 |
14.833 |
12.54 |
||
|
2 (Тип элемента 44) |
2x2 |
16.960 |
12.674 |
25.27 |
|
4x4 |
14.768 |
12.92 |
||
|
8x8 |
15.657 |
7.68 |
||
|
3 (Тип элемента 45) |
2x2 |
16.960 |
15.383 |
9.30 |
|
4x4 |
16.539 |
2.48 |
||
|
8x8 |
16.849 |
0.65 |
||
|
4 (Тип элемента 50) |
2x2 |
16.960 |
15.862 |
6.47 |
|
4x4 |
16.553 |
2.40 |
||
|
8x8 |
16.845 |
0.68 |
||
|
5 (Тип элемента 36) |
2x2 |
16.960∙10-6 |
0.014∙10-6 |
99.92 |
|
4x4 |
0.051∙10-6 |
99.70 |
||
|
8x8 |
0.197∙10-6 |
98.84 |
||
|
16x16 |
0.737∙10-6 |
95.65 |
||
|
32x32 |
2.426∙10-6 |
85.70 |
||
|
64x64 |
5.859∙10-6 |
65.45 |
||
|
128x128 |
9.654∙10-6 |
43.08 |
||
|
6 (Тип элемента 37) |
2x2 |
16.960∙10-6 |
4.494∙10-6 |
73.50 |
|
4x4 |
10.523∙10-6 |
37.95 |
||
|
8x8 |
15.480∙10-6 |
8.73 |
||
|
16x16 |
16.572∙10-6 |
2.29 |
||
|
32x32 |
16.866∙10-6 |
0.55 |
||
|
64x64 |
16.952∙10-6 |
0.05 |
||
|
128x128 |
16.976∙10-6 |
0.09 |
Замечания: При аналитическом решении значения поперечных перемещений в центре свободно опертой плоской прямоугольной пластины wq и wP от соответствующих воздействий определяются по следующим формулам:
\[ w_{q} =\frac{4\cdot q\cdot a^{4}}{\pi^{5}\cdot D}\cdot \sum\limits_{m=1}^\infty {\left\{ {\frac{1}{m^{5}}\cdot \left[ {1-\frac{\frac{m\cdot \pi \cdot b}{2\cdot a}\cdot th\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)+2}{2\cdot ch\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)}} \right]\cdot \sin \left( {\frac{m\cdot \pi }{2}} \right)} \right\}} ; \] \[ w_{P} =\frac{P\cdot a^{2}}{2\cdot \pi^{3}\cdot D}\cdot \sum\limits_{m=1}^\infty {\left\{ {\frac{1}{m^{3}}\cdot \left[ {th\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)-\frac{\frac{m\cdot \pi \cdot b}{2\cdot a}}{ch^{2}\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)}} \right]\cdot \sin^{2}\left( {\frac{m\cdot \pi }{2}} \right)} \right\}} , \quad где: \quad \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]
