Свободно опертая плоская квадратная пластина под действием равномерно распределенной по всей площади поперечной нагрузки и сосредоточенной поперечной силы в центре
Цель: Проверка точного воспроизведения значений поперечных перемещений в центре свободно опертой плоской квадратной пластины от действия равномерно распределенной по всей площади поперечной нагрузки и сосредоточенной поперечной силы в центре.
Формулировка задачи: Свободно опертая плоская квадратная пластина подвергается воздействию равномерно распределенной по всей площади поперечной нагрузки q и сосредоточенной поперечной силы в центре P. Проверить: точное воспроизведение значений поперечных перемещений в центре свободно опертой плоской квадратной пластины wq и wP от соответствующих воздействий.
Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
S. Timoshenko, S. Woinowsky-Krieger, Theory of plates and shells, New York, McGraw-Hill,1959, p. 120, 143, 202, 206.
Исходные данные:
| E = 1.7472·107 кПа | - модуль упругости материала пластины; |
| ν = 0.30 | - коэффициент Пуассона; |
| a = 2.00 м | - ширина пластины; |
| b = 2.00 м | - длина пластины; |
| h = 10-4 (10-2) м | - толщина пластины; |
| q = 1.0·10-4 кН/м2 | - значение равномерно распределенной по всей площади пластины поперечной нагрузки; |
| P = 4.0·10-4 кН | - значение сосредоточенной поперечной силы в центре пластины. |
Файлы с исходными данными:
| Расчетная модель с типом элементов 42 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 44 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 45 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 50 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 36 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 | |
| Расчетная модель с типом элементов 37 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 |
Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема четверти пластины по условиям симметрии для шести расчетных моделей:
Модель 1 – 8, 32, 128 трехузловых элемента оболочки типа 42 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных кромок пластины по направлениям степеней свободы X, Y, Z и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 2 – 4, 16, 64 четырехузловых элемента оболочки типа 44 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных кромок пластины по направлениям степеней свободы X, Y, Z и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 3 – 8, 32, 128 шестиузловых элемента оболочки типа 45 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных кромок пластины по направлениям степеней свободы X, Y, Z и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 4 – 4, 16, 64 восьмиузловых элемента оболочки типа 50 с регулярной сеткой 2x2, 4x4, 8x8. Толщина пластины – 10-4 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных кромок пластины по направлениям степеней свободы X, Y, Z и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 5 – 4, 16, 64, 256, 1024, 4096, 16384 восьмиузловых изопараметрических объемных элемента типа 36 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Толщина пластины – 10-2 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных ребер нижней поверхности пластины по направлению степени свободы Z и связей по условиям симметрии. Количество узлов в модели – 18, 50, 162, 578, 2178, 8450, 33282.
Модель 6 – 4, 16, 64, 256, 1024, 4096, 16384 двадцатиузловых изопараметрических объемных элемента типа 37 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Толщина пластины – 10-2 м. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных ребер нижней поверхности пластины по направлению степени свободы Z и связей по условиям симметрии. Количество узлов в модели – 51, 155, 531, 1955, 7491, 29315, 115971.
Результаты решения в SCAD
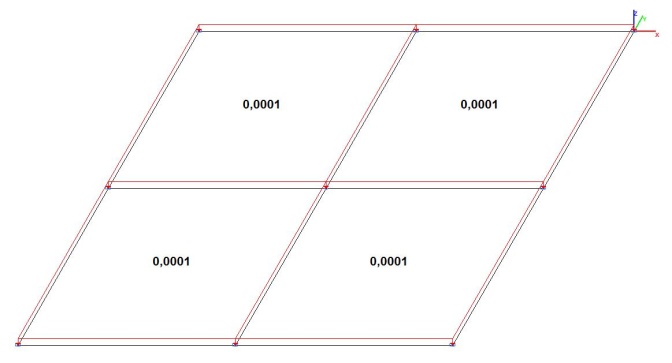
Модель 1. Расчетная схема
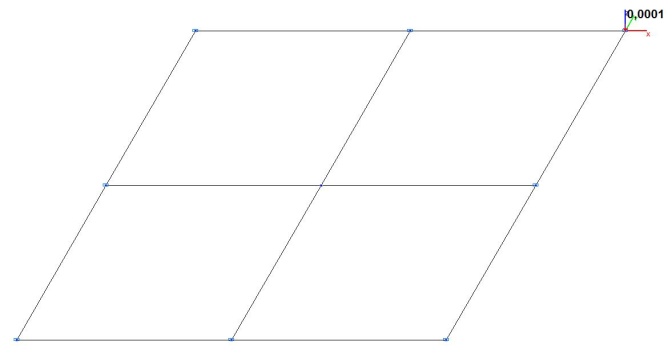
Модель 1. Деформированная схема






Модель 1. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)

Модель 2. Расчетная схема
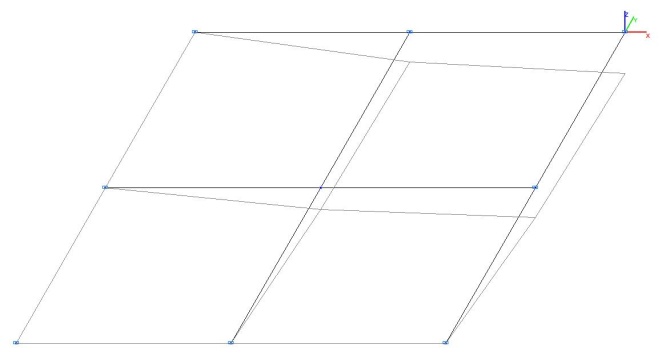
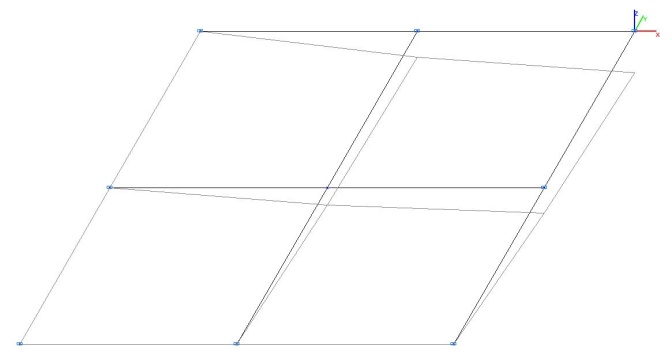
Модель 2. Деформированная схема
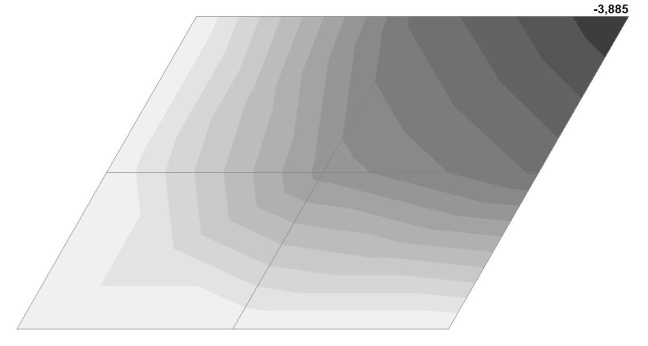
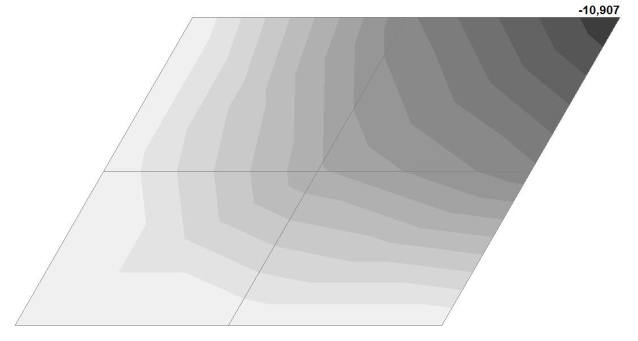
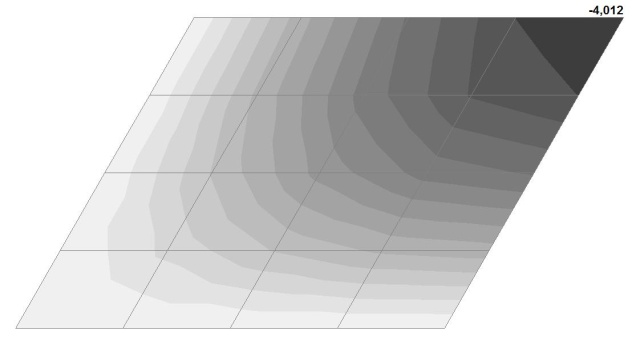
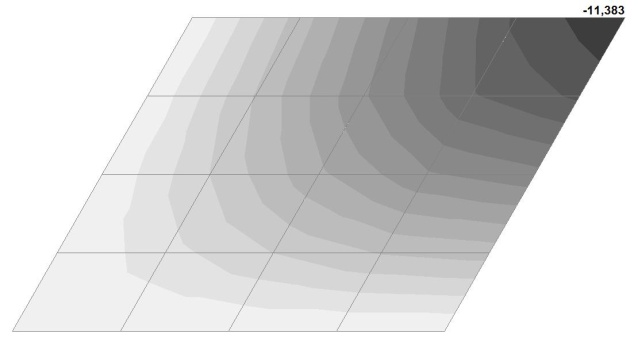


Модель 2. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)
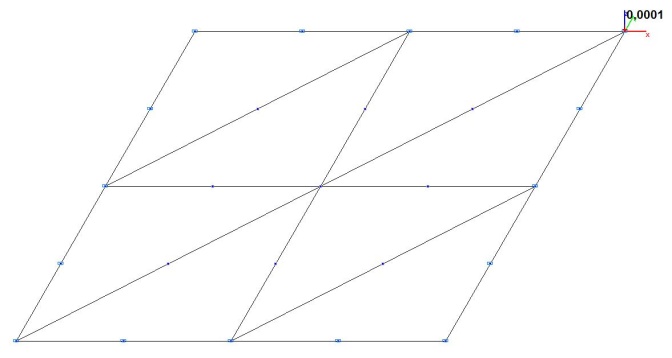
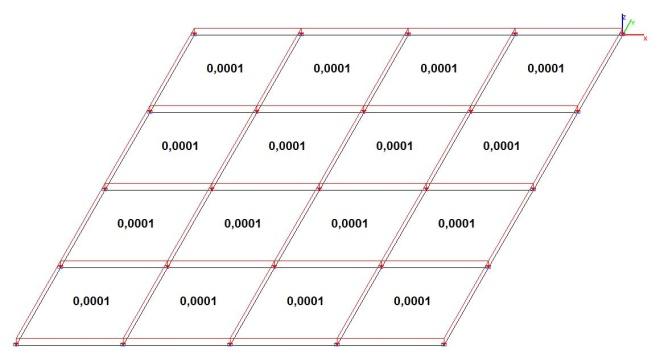
Модель 3. Расчетная схема
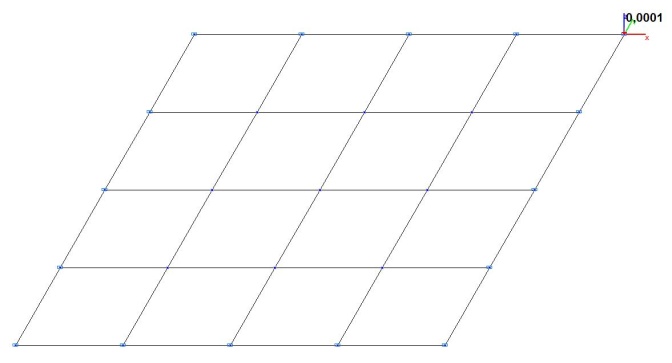
Модель 3. Деформированная схема






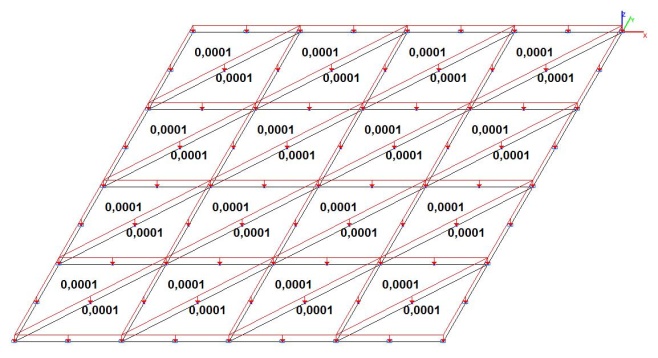
Модель 3. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)
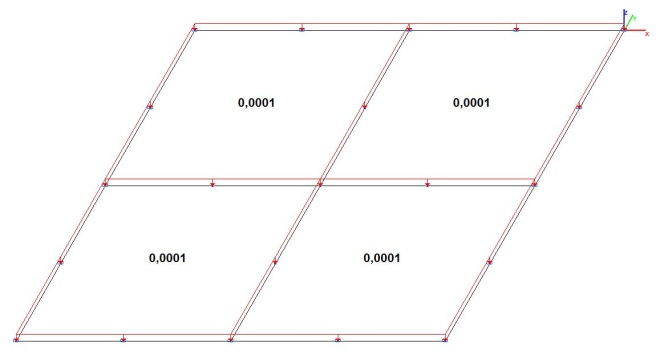
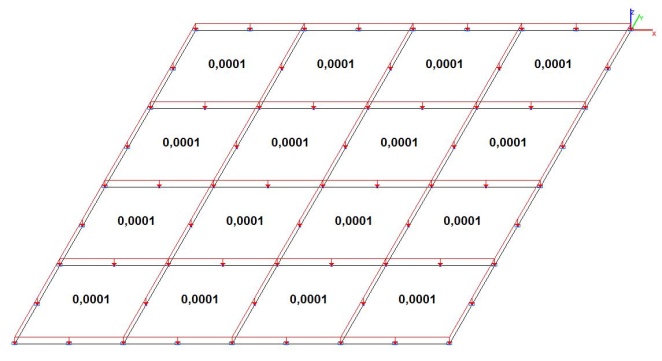

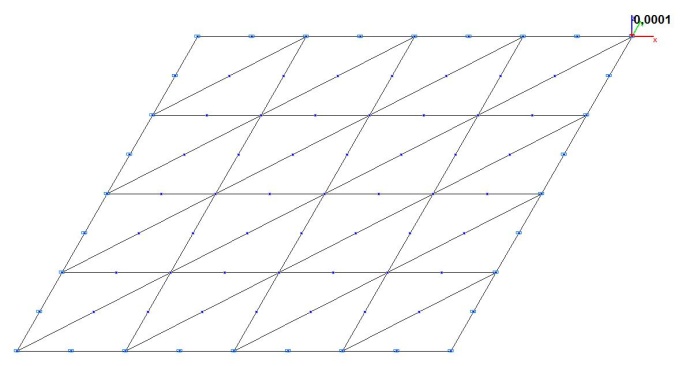
Модель 4. Расчетная схема
Модель 4. Деформированная схема
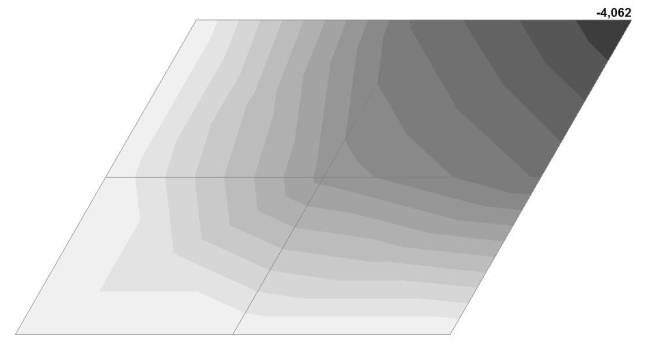
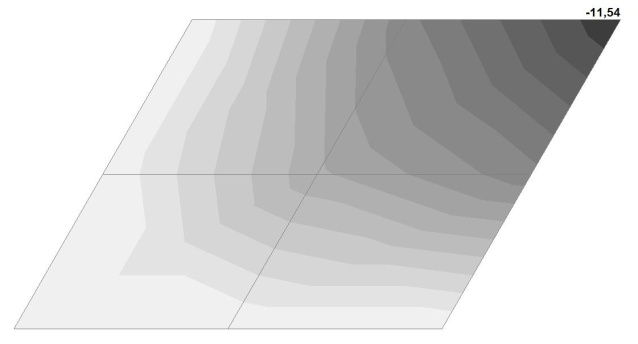
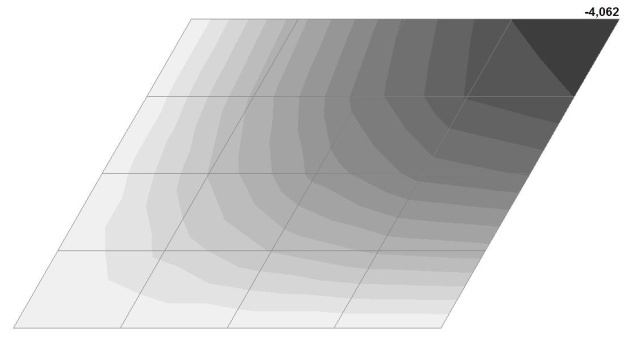
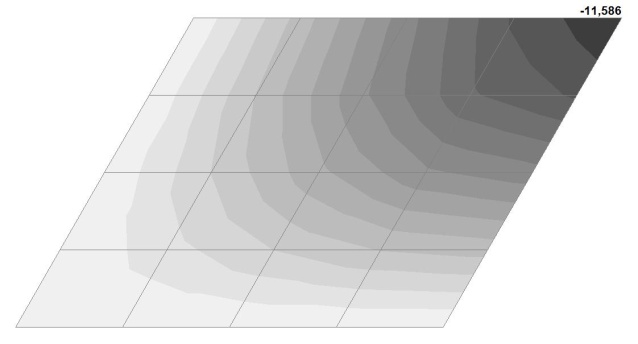
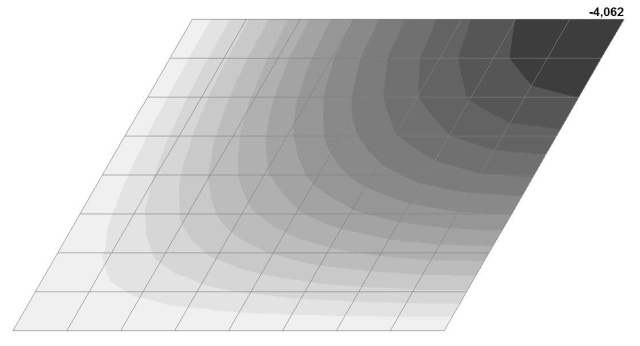

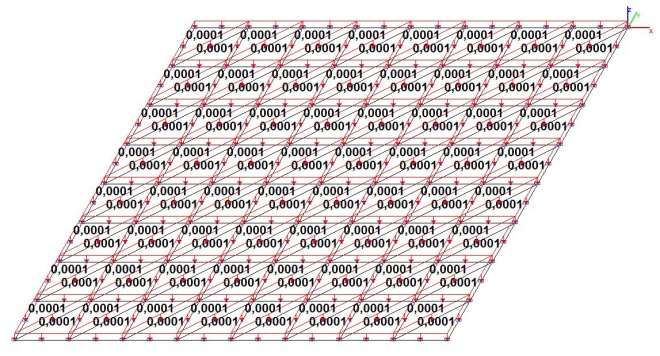
Модель 4. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)
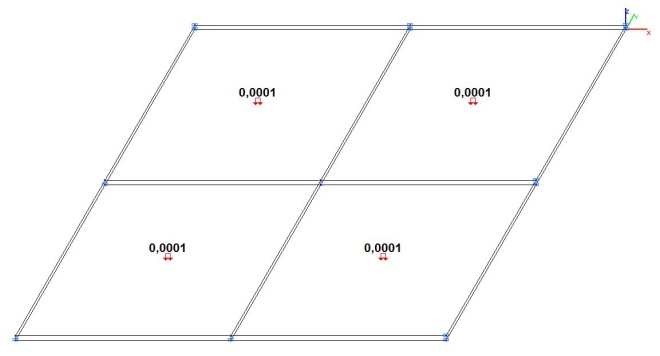
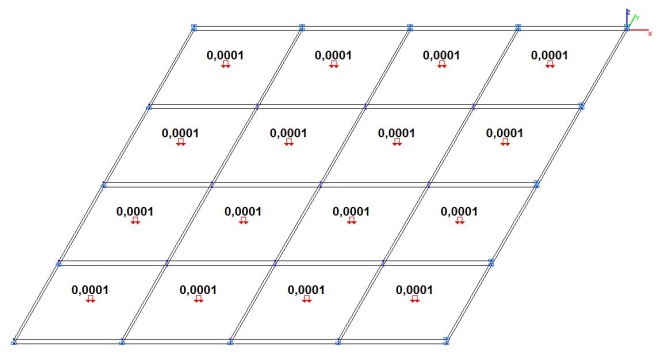
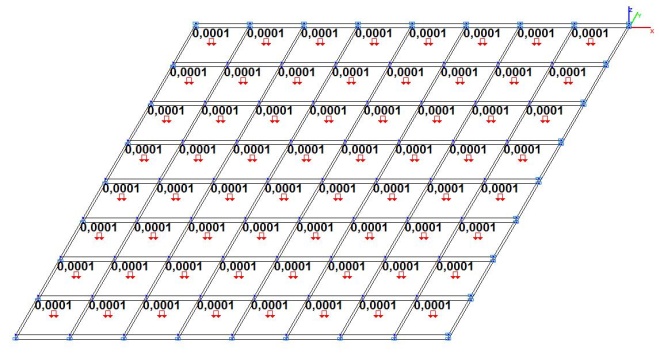
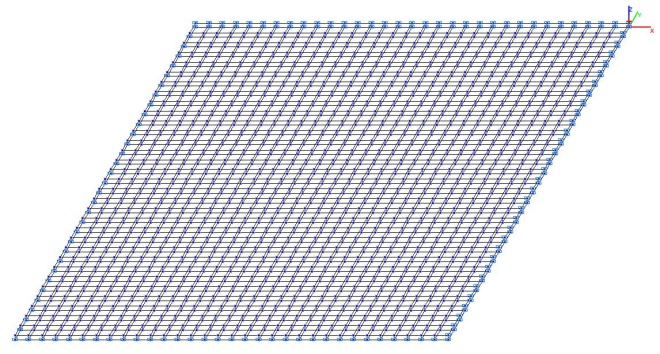




Модель 5. Расчетная схема
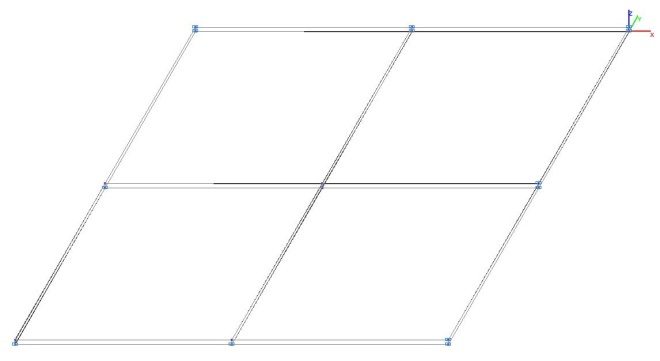
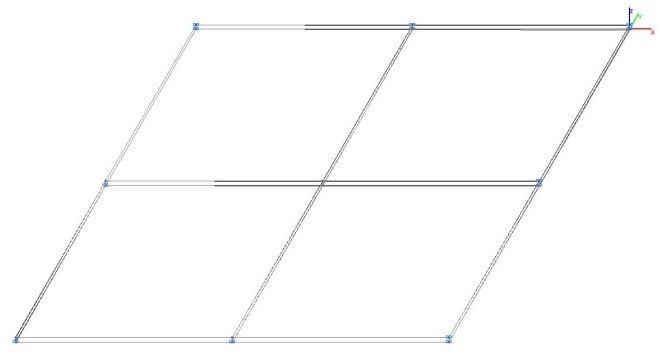
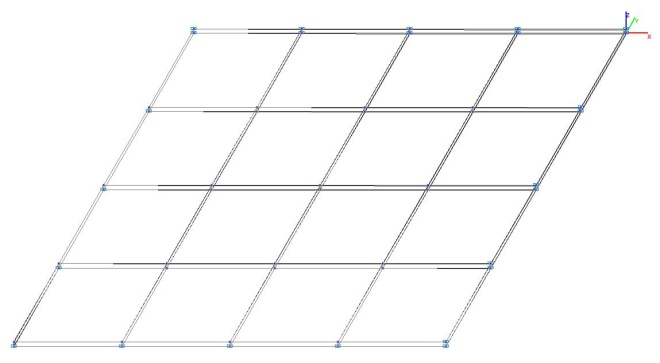




Модель 5. Деформированная схема









Модель 5. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)
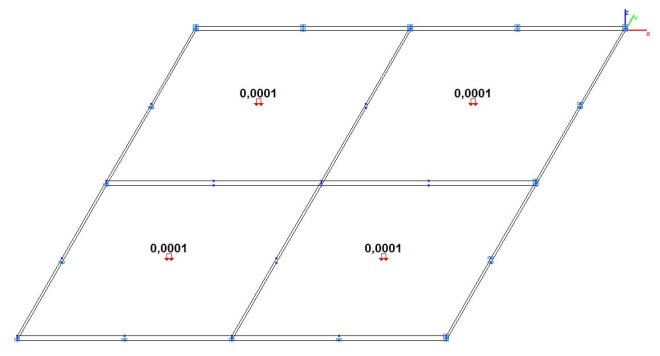
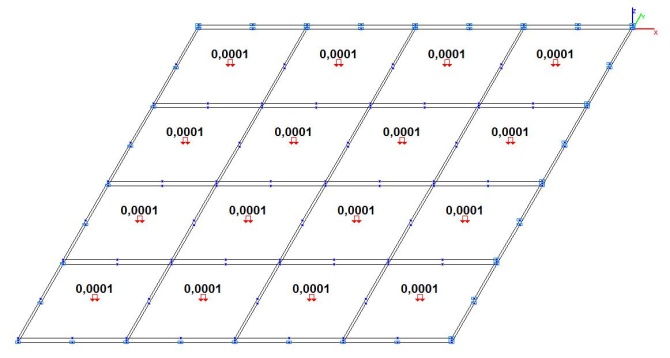
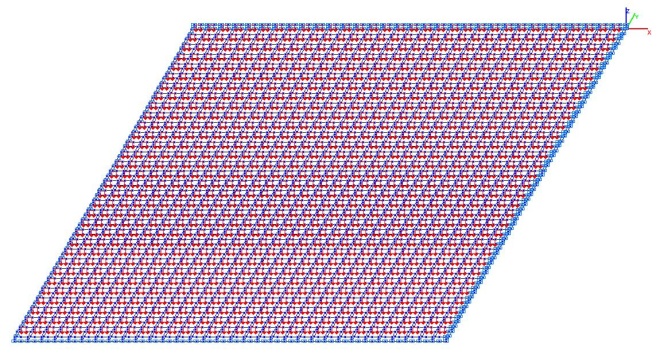





Модель 6. Расчетная схема
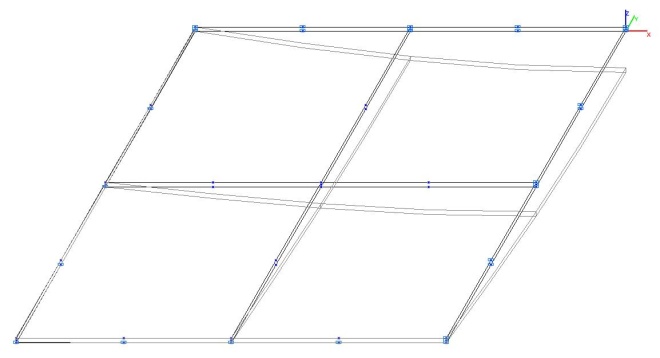





Модель 6. Деформированная схема
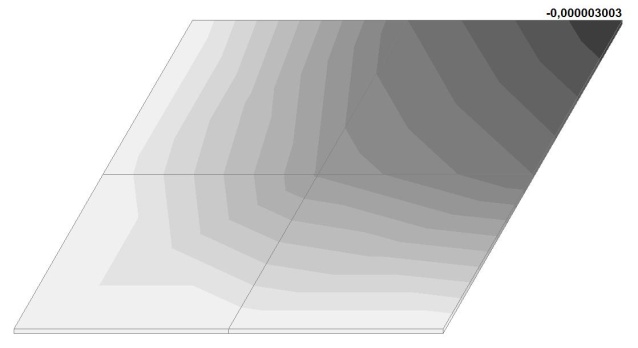
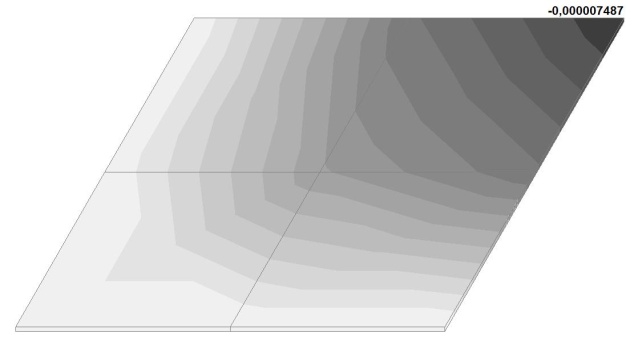










Модель 6. Значения поперечных перемещений в центре свободно опертой квадратной пластины wq и wP (м, м)
Сравнение решений:
Поперечные перемещения в центре свободно опертой плоской квадратной пластины wq от воздействия равномерно распределенной по всей площади поперечной нагрузки q
|
Модель |
Сетка конечных элементов |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
2x2 |
4.062 |
3.808 |
6.25 |
|
4x4 |
3.998 |
1.58 |
||
|
8x8 |
4.046 |
0.39 |
||
|
2 (Тип элемента 44) |
2x2 |
4.062 |
3.885 |
4.36 |
|
4x4 |
4.012 |
1.23 |
||
|
8x8 |
4.049 |
0.32 |
||
|
3 (Тип элемента 45) |
2x2 |
4.062 |
4.062 |
0.00 |
|
4x4 |
4.062 |
0.00 |
||
|
8x8 |
4.062 |
0.00 |
||
|
4 (Тип элемента 50) |
2x2 |
4.062 |
4.062 |
0.00 |
|
4x4 |
4.062 |
0.00 |
||
|
8x8 |
4.062 |
0.00 |
||
|
5 (Тип элемента 36) |
2x2 |
4.062•10-6 |
0.009•10-6 |
99.78 |
|
4x4 |
0.037•10-6 |
99.09 |
||
|
8x8 |
0.144•10-6 |
96.45 |
||
|
16x16 |
0.509•10-6 |
87.47 |
||
|
32x32 |
1.308•10-6 |
67.80 |
||
|
64x64 |
2.471•10-6 |
39.17 |
||
|
128x128 |
3.061•10-6 |
24.64 |
||
|
6 (Тип элемента 37) |
2x2 |
4.062•10-6 |
3.003•10-6 |
26.07 |
|
4x4 |
4.025•10-6 |
0.91 |
||
|
8x8 |
4.060•10-6 |
0.05 |
||
|
16x16 |
4.068•10-6 |
0.15 |
||
|
32x32 |
4.073•10-6 |
0.27 |
||
|
64x64 |
4.077•10-6 |
0.37 |
||
|
128x128 |
4.078•10-6 |
0.39 |
Поперечные перемещения в центре свободно опертой плоской квадратной пластины wP от воздействия сосредоточенной поперечной силы в центре P
|
Модель |
Сетка конечных элементов |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
2x2 |
11.600 |
10.236 |
11.76 |
|
4x4 |
11.205 |
3.41 |
||
|
8x8 |
11.490 |
0.95 |
||
|
2 (Тип элемента 44) |
2x2 |
11.600 |
10.907 |
5.97 |
|
4x4 |
11.383 |
1.87 |
||
|
8x8 |
11.537 |
0.54 |
||
|
3 (Тип элемента 45) |
2x2 |
11.600 |
11.574 |
0.22 |
|
4x4 |
11.594 |
0.05 |
||
|
8x8 |
11.599 |
0.01 |
||
|
4 (Тип элемента 50) |
2x2 |
11.600 |
11.540 |
0.52 |
|
4x4 |
11.586 |
0.12 |
||
|
8x8 |
11.597 |
0.02 |
||
|
5 (Тип элемента 36) |
2x2 |
11.600•10-6 |
0.028•10-6 |
99.76 |
|
4x4 |
0.104•10-6 |
99.10 |
||
|
8x8 |
0.394•10-6 |
96.60 |
||
|
16x16 |
1.393•10-6 |
87.98 |
||
|
32x32 |
3.595•10-6 |
69.01 |
||
|
64x64 |
6.935•10-6 |
40.21 |
||
|
128x128 |
8.691•10-6 |
25.08 |
||
|
6 (Тип элемента 37) |
2x2 |
11.600•10-6 |
7.487•10-6 |
35.46 |
|
4x4 |
11.009•10-6 |
5.09 |
||
|
8x8 |
11.467•10-6 |
1.15 |
||
|
16x16 |
11.586•10-6 |
0.12 |
||
|
32x32 |
11.623•10-6 |
0.20 |
||
|
64x64 |
11.637•10-6 |
0.32 |
||
|
128x128 |
11.644•10-6 |
0.38 |
Замечания: При аналитическом решении значения поперечных перемещений в центре свободно опертой плоской квадратной пластины wq и wP от соответствующих воздействий определяются по следующим формулам:
\[ w_{q} =\frac{4\cdot q\cdot a^{4}}{\pi^{5}\cdot D}\cdot \sum\limits_{m=1}^\infty {\left\{ {\frac{1}{m^{5}}\cdot \left[ {1-\frac{\frac{m\cdot \pi \cdot b}{2\cdot a}\cdot th\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)+2}{2\cdot ch\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)}} \right]\cdot \sin \left( {\frac{m\cdot \pi }{2}} \right)} \right\}} ; \] \[ w_{P} =\frac{P\cdot a^{2}}{2\cdot \pi^{3}\cdot D}\cdot \sum\limits_{m=1}^\infty {\left\{ {\frac{1}{m^{3}}\cdot \left[ {th\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)-\frac{\frac{m\cdot \pi \cdot b}{2\cdot a}}{ch^{2}\left( {\frac{m\cdot \pi \cdot b}{2\cdot a}} \right)}} \right]\cdot \sin^{2}\left( {\frac{m\cdot \pi }{2}} \right)} \right\}} ,\quad где:\quad \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]
