Почти несжимаемый толстостенный цилиндр в условиях плоской деформации под действием равномерно распределенного внутреннего давления

Цель: Проверка точного воспроизведения значений радиальных перемещений внутренней поверхности почти несжимаемого толстостенного цилиндра в условиях плоской деформации от действия равномерно распределенного внутреннего давления.

Файлы с исходными данными:

Nearly_incompressible_thick_cylinder_Shell_42_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_Shell_42_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Shell_42_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 42 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999
Nearly_incompressible_thick_cylinder_Shell_44_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_Shell_44_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Shell_44_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 44 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999
Nearly_incompressible_thick_cylinder_Shell_45_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_Shell_45_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Shell_45_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 45 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999
Nearly_incompressible_thick_cylinder_Shell_50_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_Shell_50_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Shell_50_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 50 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999
Nearly_incompressible_thick_cylinder_ Solid _36_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_ Solid _36_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Solid_36_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 36 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999
Nearly_incompressible_thick_cylinder_ Solid _37_Poisson_ratio_049_.spr Nearly_incompressible_thick_cylinder_ Solid _37_Poisson_ratio_0499_.spr Nearly_incompressible_thick_cylinder_Solid_37_Poisson_ratio_04999_.spr	Расчетная модель с типом элементов 37 для материала с коэффициентом Пуассона 0.49, 0.499, 0.4999

Формулировка задачи: Почти несжимаемый толстостенный цилиндр находится в условиях плоской деформации и подвергается воздействию равномерно распределенного внутреннего давления p. Проверить: точное воспроизведение значений радиальных перемещений внутренней поверхности u.

Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.

Исходные данные:

E = 1000 кПа	- модуль упругости материала толстостенного цилиндра;
ν = 0.49; 0.499; 0.4999	- коэффициент Пуассона;
R_i = 3.00 м	- радиус внутренней поверхности толстостенного цилиндра;
R_e = 9.00 м	- радиус внешней поверхности толстостенного цилиндра;
p = 1.0 кПа	- значения равномерно распределенного внутреннего давления.

Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема сектора толстостенного цилиндра толщиной 1.00 м с центральным углом θ = 10° по условиям симметрии для шести расчетных моделей:

Модель 1 – 10 трехузловых элементов оболочки типа 42 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 12 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степеням свободы Z, UZ. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по линии p = 1.0 кН/м. Количество узлов в модели – 24.

Модель 2 – 5 четырехузловых элементов оболочки типа 44 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 12 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степеням свободы Z, UZ. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по линии p = 1.0 кН/м. Количество узлов в модели – 24.

Модель 3 – 10 шестиузловых элементов оболочки типа 45 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 22 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степеням свободы Z, UZ. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по линии p = 1.0 кН/м. Количество узлов в модели – 55.

Модель 4 – 5 восьмиузловых элементов оболочки типа 50 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 22 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степеням свободы Z, UZ. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по линии p = 1.0 кН/м. Количество узлов в модели – 50.

Модель 5 – 5 восьмиузловых изопараметрических объемных элементов типа 36 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 24 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степени свободы Z. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по грани p = 1.0 кН/м². Количество узлов в модели – 50.

Модель 6 – 5 двадцатиузловых изопараметрических объемных элементов типа 37 неравных размеров с разбивкой сетки в радиальном направлении 3.00 м, 3.50 м, 4.20 м, 5.20 м, 6.75 м, 9.00 м . Обеспечение граничных условий достигается за счет введения 56 стержневых элементов пространственной фермы типа 4 повышенной продольной жесткости (EF = 10⁶ кН) в тангенциальном направлении (ортогонально боковым поверхностям сектора). На опорные узлы стержневых элементов накладываются связи по степеням свободы X, Y, Z. Геометрическая неизменяемость достигается за счет наложения связей на боковые поверхности сектора по степени свободы Z. По внутренней поверхности цилиндра прикладывается нагрузка на элемент по грани p = 1.0 кН/м². Количество узлов в модели – 124.

Результаты решения в SCAD

Модель 1. Расчетная схема

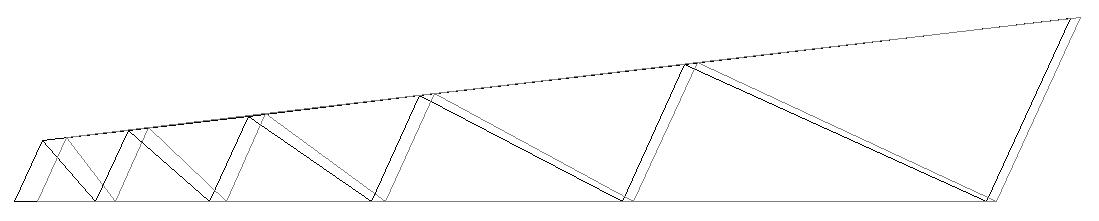
Модель 1. Деформированная схема

Модель 1. Значения перемещений по направлению оси X общей системы координат (м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

Модель 2. Расчетная схема

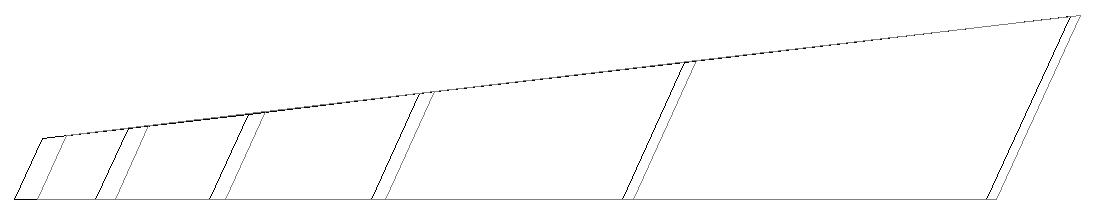
Модель 2. Деформированная схема

Модель 2. Значения перемещений по направлению оси X общей системы координат (м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

Модель 3. Расчетная схема

Модель 3. Деформированная схема

Модель 3. Значения перемещений по направлению оси X общей системы координат (м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

Модель 4. Расчетная схема

Модель 4. Деформированная схема

Модель 4. Значения перемещений по направлению оси X общей системы координат (м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

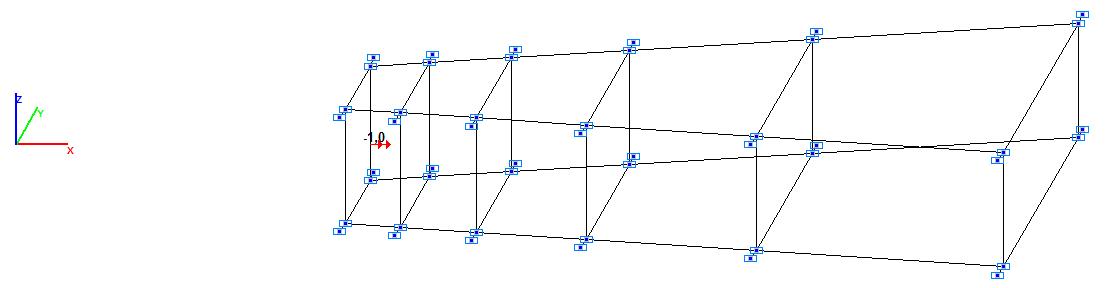
Модель 5. Расчетная схема

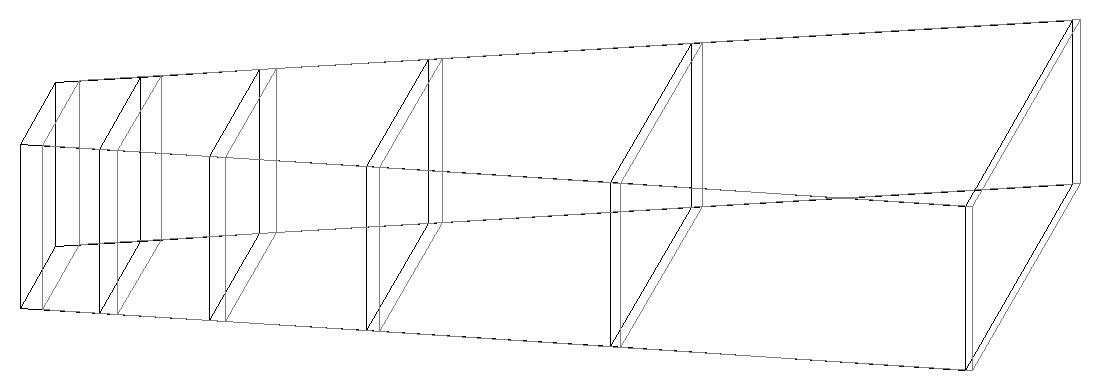
Модель 5. Деформированная схема

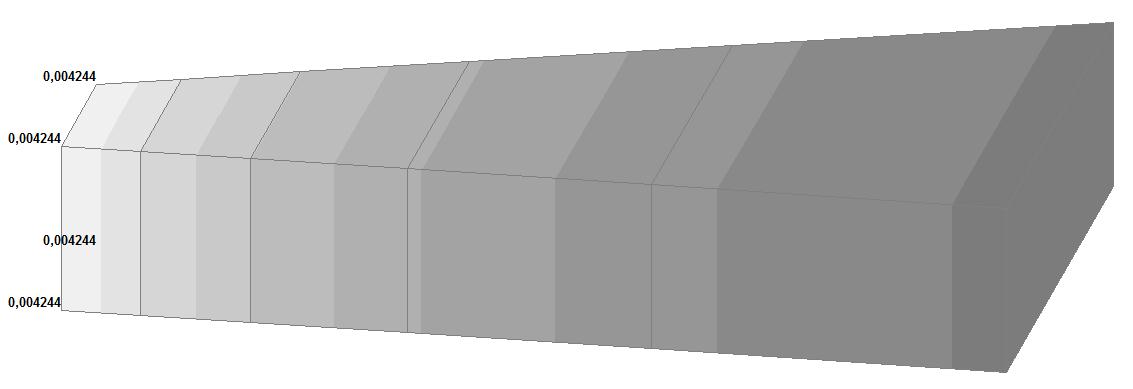
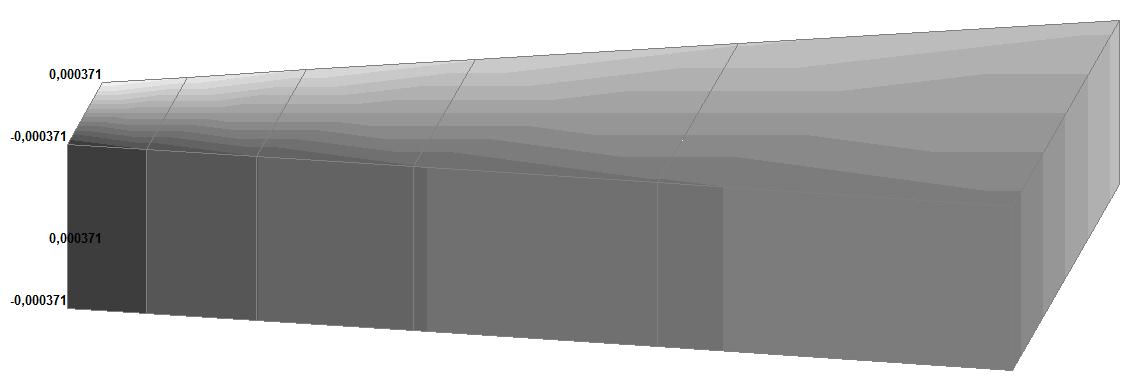
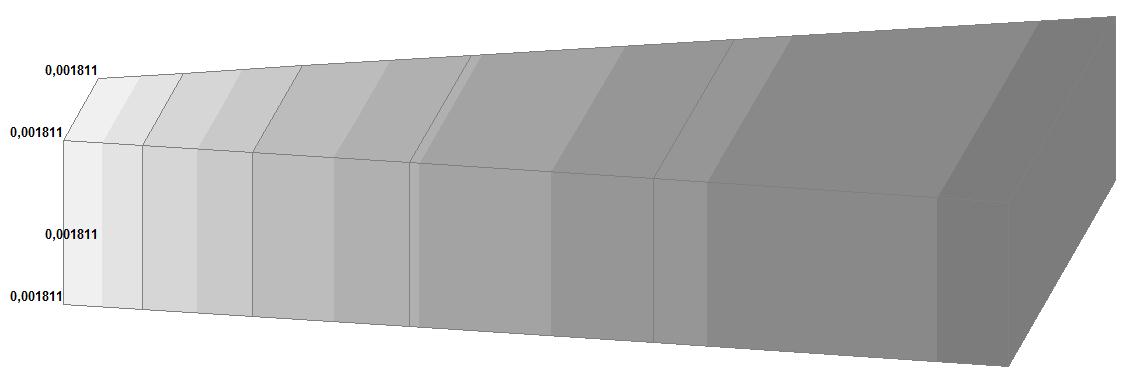
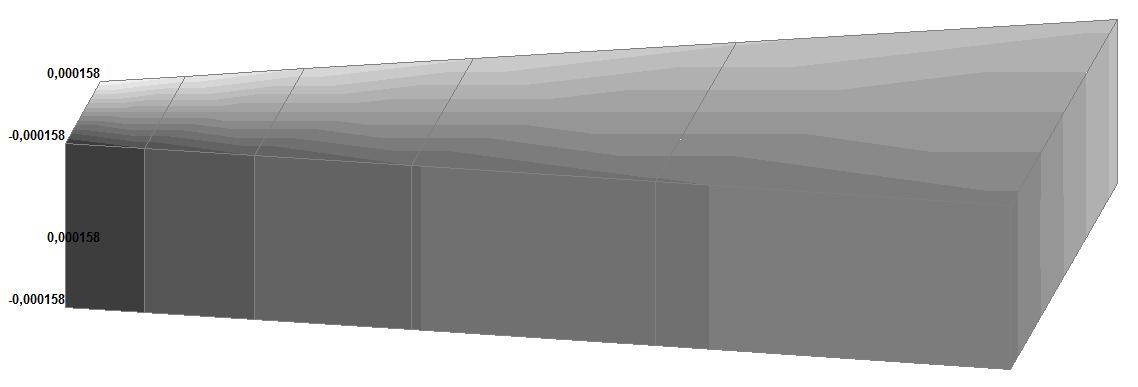
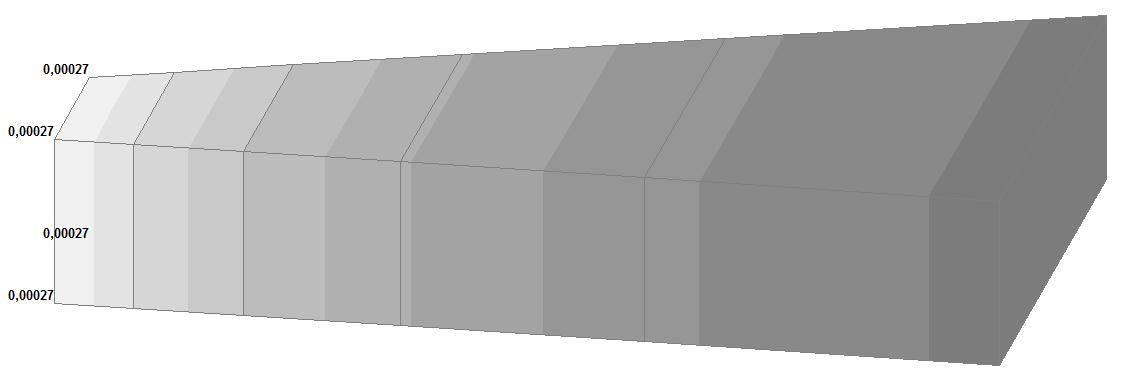
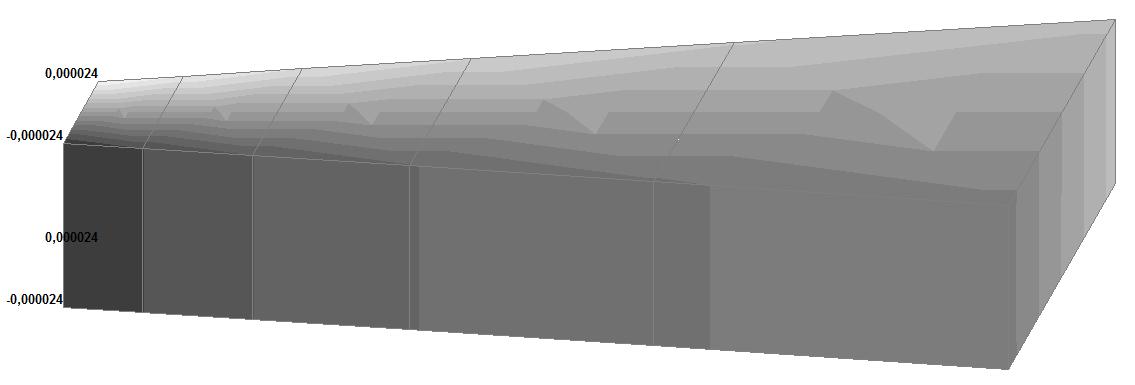
Модель 5. Значения перемещений по направлению осей X и Y общей системы координат (м, м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

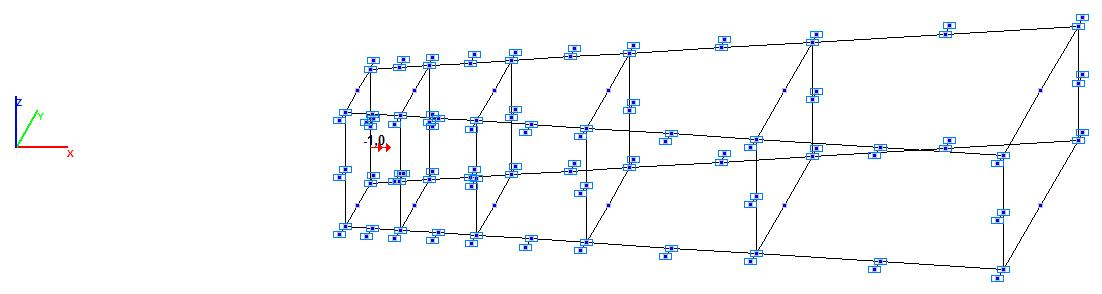
Модель 6. Расчетная схема

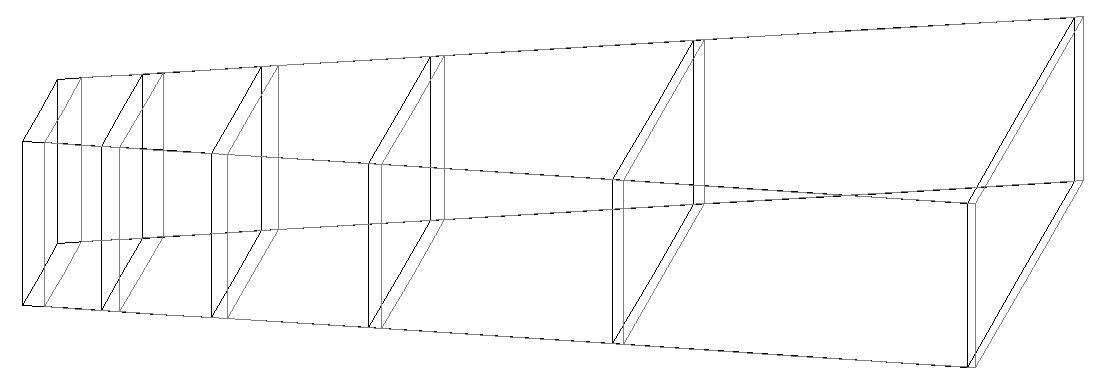
Модель 6. Деформированная схема

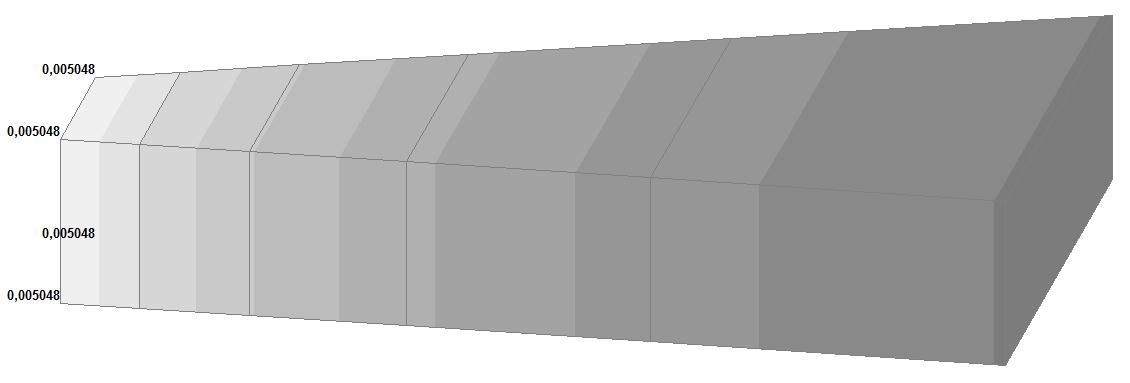
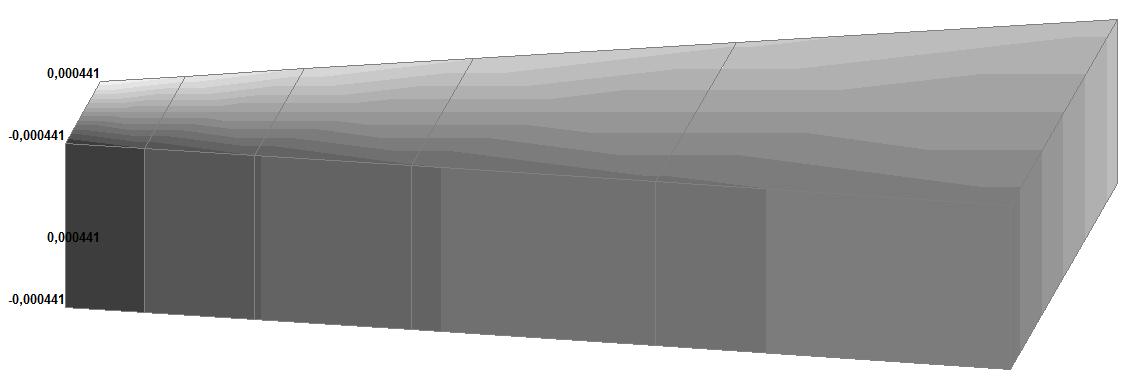
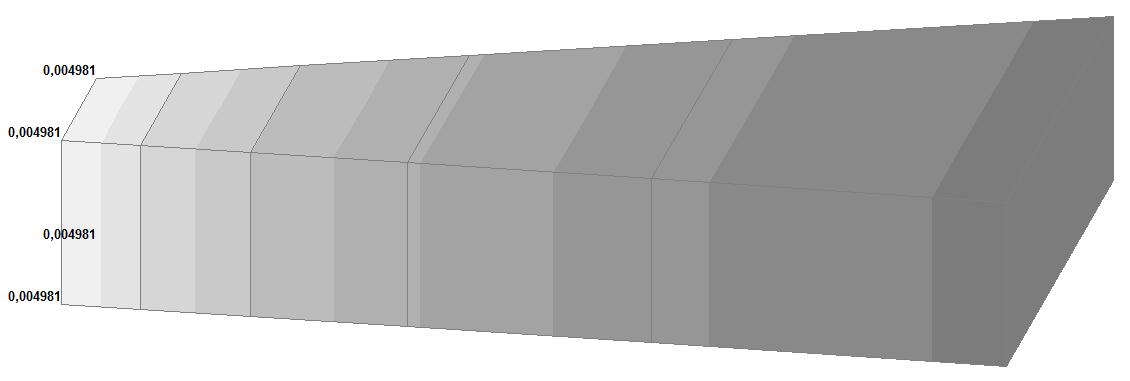
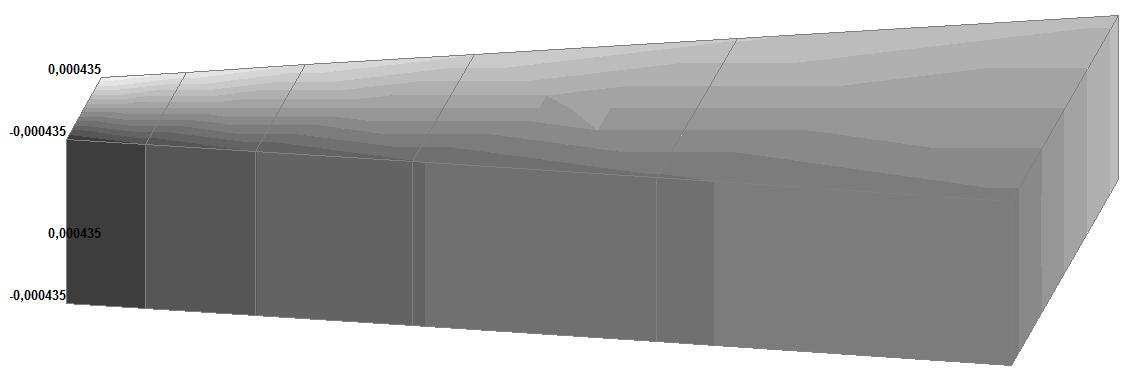
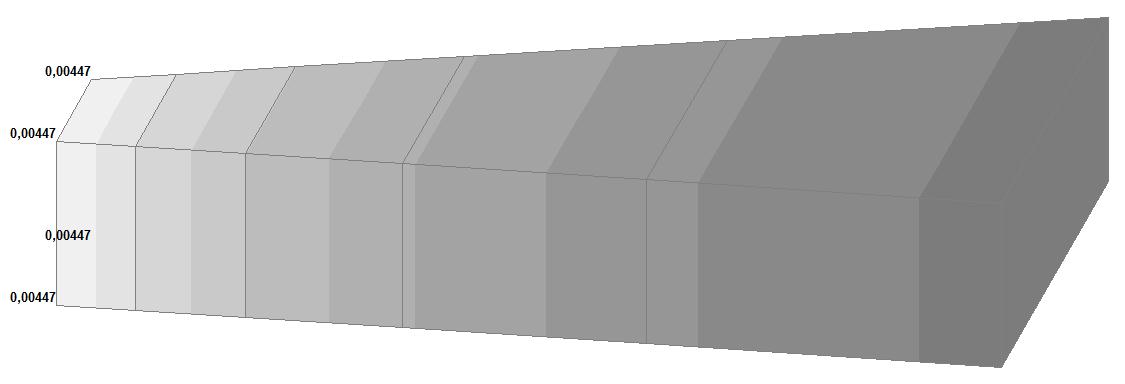
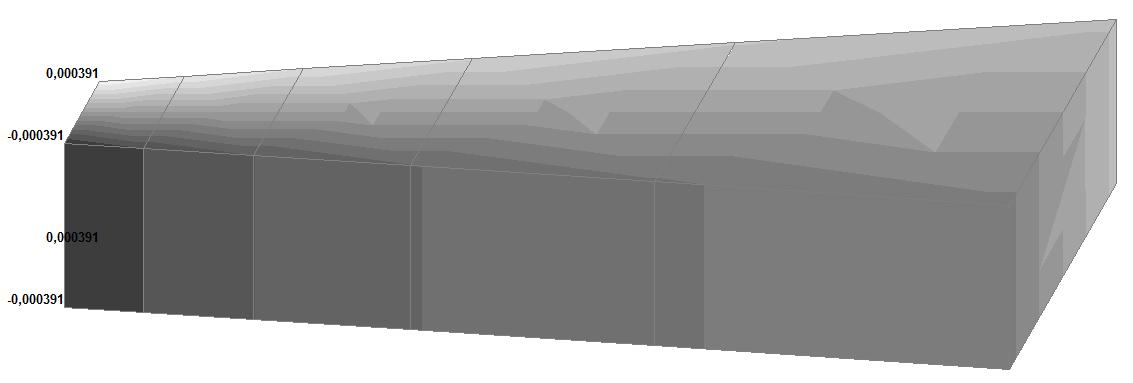
Модель 6. Значения перемещений по направлению осей X и Y общей системы координат (м, м) для материалов толстостенного цилиндра с коэффициентами Пуассона 0.49; 0.499; 0.4999

Сравнение решений:

Радиальные перемещения внутренней поверхности толстостенного цилиндра u (м) для материалов с коэффициентами Пуассона 0.49; 0.499; 0.4999

Модель	Коэффициент Пуассона	Теория	SCAD	Отклонение, %
1 (Тип элемента 42)	0.49	0.005040	0.005093	1.05
	0.499	0.005060	0.005118	1.15
	0.4999	0.005062	0.005121	1.17
2 (Тип элемента 44)	0.49	0.005040	0.005138	1.94
	0.499	0.005060	0.005163	2.04
	0.4999	0.005062	0.005166	2.05
3 (Тип элемента 45)	0.49	0.005040	0.005195	3.08
	0.499	0.005060	0.005222	3.20
	0.4999	0.005062	0.005225	3.22
4 (Тип элемента 50)	0.49	0.005040	0.005193	3.04
	0.499	0.005060	0.005222	3.20
	0.4999	0.005062	0.005223	3.18
5 (Тип элемента 36)	0.49	0.005040	√(0.004244² + + 0.000371²) = = 0.004260	15.48
	0.499	0.005060	√(0.001811² + + 0.000158²) = = 0.001818	64.07
	0.4999	0.005062	√(0.000270² + + 0.000024²) = = 0.000271	94.65
6 (Тип элемента 37)	0.49	0.005040	√(0.005048² + + 0.000441²) = = 0.005067	0.54
	0.499	0.005060	√(0.004981² + + 0.000435²) = = 0.005000	1.19
	0.4999	0.005062	√(0.004470² + + 0.000391²) = = 0.004487	11.36

Замечания: При аналитическом решении радиальные перемещения внутренней поверхности почти несжимаемого толстостенного цилиндра в условиях плоской деформации u от действия равномерно распределенного внутреннего давления определяются по следующим формулам:

\[ u=\frac{\left( {1+\nu } \right)\cdot p\cdot R_{i}^{2}}{E\cdot \left( {R_{e} ^{2}-R_{i}^{2}} \right)}\cdot \left[ {\frac{R_{e}^{2}}{R_{i} }+\left( {1-2\cdot \nu } \right)\cdot R_{i} } \right]. \]