SCAD: Патологические тесты

Свободная оболочка полусферы с круговым полюсным отверстием под действием двух ортогональных пар взаимно уравновешенных радиально растягивающих и радиально сжимающих сил на экваторе

Цель: Проверка точного воспроизведения значений поперечных перемещений свободной оболочки полусферы с круговым полюсным отверстием по направлению действия двух ортогональных пар взаимно уравновешенных радиально растягивающих и  радиально сжимающих сил на экваторе.

Файлы с исходными данными:

Quadrant_of_a_spherical_shell_42_Mesh_2x2.spr
Quadrant_of_a_spherical_shell_42_Mesh_4x4.spr
Quadrant_of_a_spherical_shell_42_Mesh_8x8.spr
Quadrant_of_a_spherical_shell_42_Mesh_16x16.spr
Quadrant_of_a_spherical_shell_42_Mesh_32x32.spr

 Расчетная модель с типом элементов 42 для сеток 2x2, 4x4, 8x8, 16x16, 32x32

Quadrant_of_a_spherical_shell_44_Mesh_2x2.spr
Quadrant_of_a_spherical_shell_44_Mesh_4x4.spr
Quadrant_of_a_spherical_shell_44_Mesh_8x8.spr
Quadrant_of_a_spherical_shell_44_Mesh_16x16.spr
Quadrant_of_a_spherical_shell_44_Mesh_32x32.spr

 Расчетная модель с типом элементов 44 для сеток 2x2, 4x4, 8x8, 16x16, 32x32

Quadrant_of_a_spherical_shell_45_Mesh_2x2.spr
Quadrant_of_a_spherical_shell_45_Mesh_4x4.spr
Quadrant_of_a_spherical_shell_45_Mesh_8x8.spr
Quadrant_of_a_spherical_shell_45_Mesh_16x16.spr
Quadrant_of_a_spherical_shell_45_Mesh_32x32.spr

 Расчетная модель с типом элементов 45 для сеток 2x2, 4x4, 8x8, 16x16, 32x32

Quadrant_of_a_spherical_shell_50_Mesh_2x2.spr
Quadrant_of_a_spherical_shell_50_Mesh_4x4.spr
Quadrant_of_a_spherical_shell_50_Mesh_8x8.spr
Quadrant_of_a_spherical_shell_50_Mesh_16x16.spr
Quadrant_of_a_spherical_shell_50_Mesh_32x32.spr

 Расчетная модель с типом элементов 50 для сеток 2x2, 4x4, 8x8, 16x16, 32x32

Quadrant_of_a_spherical_solid_36_Mesh_2x2.spr
Quadrant_of_a_spherical_solid_36_Mesh_4x4.spr
Quadrant_of_a_spherical_solid_36_Mesh_8x8.spr
Quadrant_of_a_spherical_solid_36_Mesh_16x16.spr
Quadrant_of_a_spherical_solid_36_Mesh_32x32.spr
Quadrant_of_a_spherical_solid_36_Mesh_64x64.spr
Quadrant_of_a_spherical_solid_36_Mesh_128x128.spr
Quadrant_of_a_spherical_solid_36_Mesh_256x256.spr
Quadrant_of_a_spherical_solid_36_Mesh_512x512.spr

 Расчетная модель с типом элементов 36 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128, 256x256, 512x512

Quadrant_of_a_spherical_solid_37_Mesh_2x2.spr
Quadrant_of_a_spherical_solid_37_Mesh_4x4.spr
Quadrant_of_a_spherical_solid_37_Mesh_8x8.spr
Quadrant_of_a_spherical_solid_37_Mesh_16x16.spr
Quadrant_of_a_spherical_solid_37_Mesh_32x32.spr
Quadrant_of_a_spherical_solid_37_Mesh_64x64.spr
Quadrant_of_a_spherical_solid_37_Mesh_128x128.spr

 Расчетная модель с типом элементов 37 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128

 

Формулировка задачи: Свободная оболочка полусферы с круговым полюсным отверстием подвергается воздействию двух ортогональных пар взаимно уравновешенных радиально растягивающих и радиально сжимающих сил F на экваторе. Проверить: точное воспроизведение значений поперечных перемещений свободной оболочки полусферы wFX и wFY по направлению действия сил на экваторе.

Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
L. S. D. Morley, A. J. Morris, Conflict between finite elements and shell theory, London, Royal aircraft establishment report, 1978.

Исходные данные:

E = 6.825·107 кПа - модуль упругости материала оболочки полусферы;
ν = 0.30 - коэффициент Пуассона;
R = 10.00 м - радиус срединной поверхности оболочки полусферы;
2·θ = 2·18° - центральный угол поверхности кругового отверстия оболочки полусферы;
h = 0.04 м - толщина оболочки полусферы;
FX = + 2.0 кН - значения сосредоточенных радиально растягивающих сил, действующих на экваторе оболочки полусферы;
FY = – 2.0 кН - значения сосредоточенных радиально сжимающих сил, действующих на экваторе оболочки полусферы.


Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема четверти оболочки полусферы по условиям симметрии для шести расчетных моделей:

Модель 1 - 8, 32, 128, 512, 2048 трехузловых элемента оболочки типа 42 с регулярной сеткой 2x2, 4x4, 8x8, 16x16, 32x32. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 9, 25, 81, 289, 1089.

Модель 2 - 4, 16, 64, 256, 1024 четырехузловых элемента оболочки типа 44 с регулярной сеткой 2x2, 4x4, 8x8, 16x16, 32x32. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 9, 25, 81, 289,1089.

Модель 3 - 8, 32, 128, 512, 2048 шестиузловых элемента оболочки типа 45 с регулярной сеткой 2x2, 4x4, 8x8, 16x16, 32x32. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 25, 81, 289, 1089, 4225.

Модель 4 - 4, 16, 64, 256, 1024 восьмиузловых элемента оболочки типа 50 с регулярной сеткой 2x2, 4x4, 8x8, 16x16, 32x32. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 21, 65, 225, 833, 3201.

Модель 5 - 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144 восьмиузловых изопараметрических объемных элемента типа 36 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1, 256x256x1, 512x512x1. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 18, 50, 162, 578, 2178, 8450, 33282, 132149, 526338.

Модель 6 - 4, 16, 64, 256, 1024, 4096, 16384 двадцатиузловых изопараметрических объемных элемента типа 37 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Обеспечение граничных условий и геометрической неизменяемости достигается за счет наложения связей по условиям симметрии. Количество узлов в модели – 51, 155, 531, 1955, 7491, 29315, 115971.

Результаты решения в SCAD




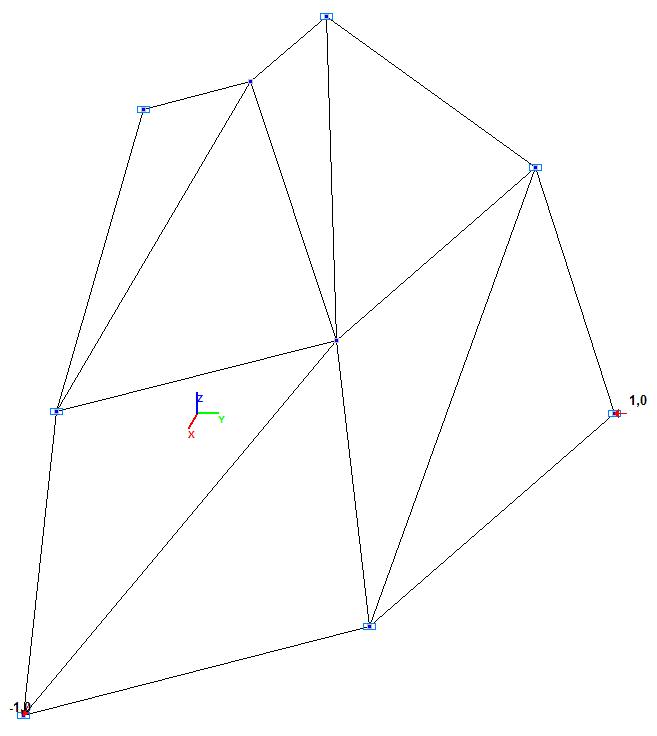
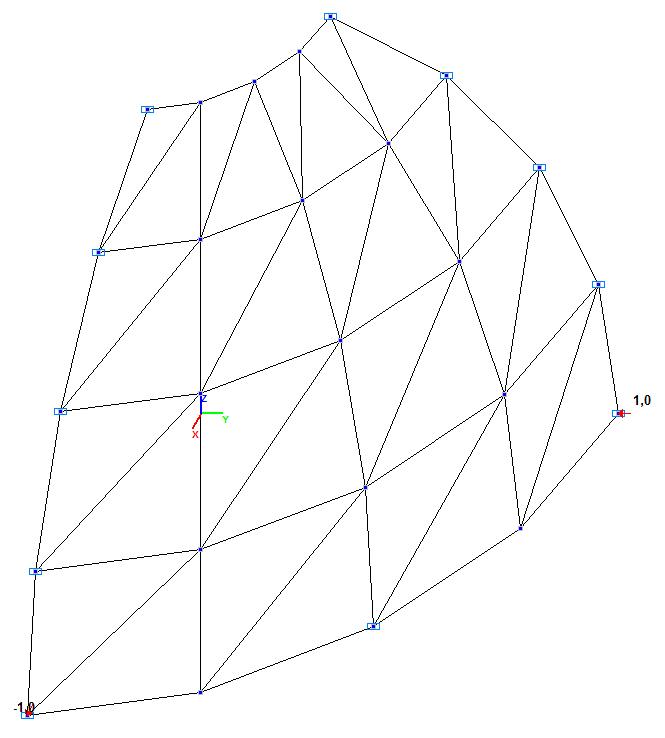
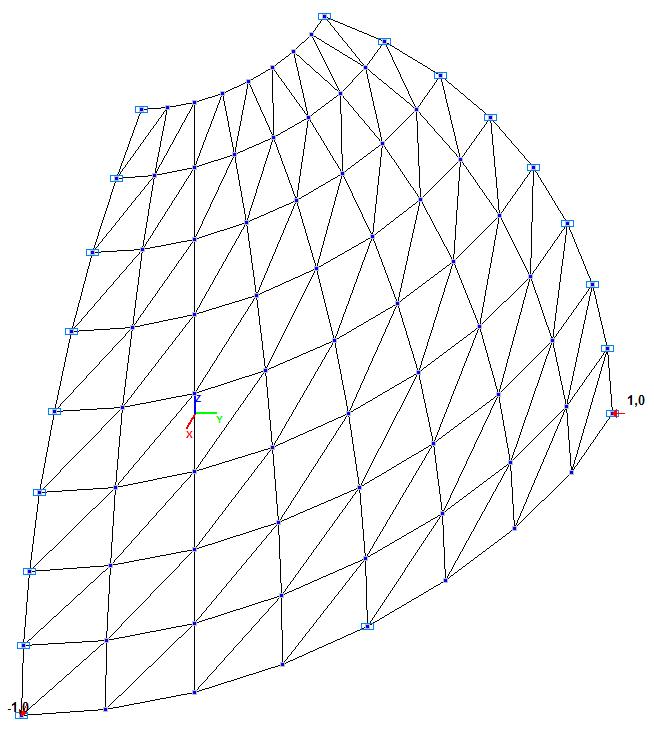
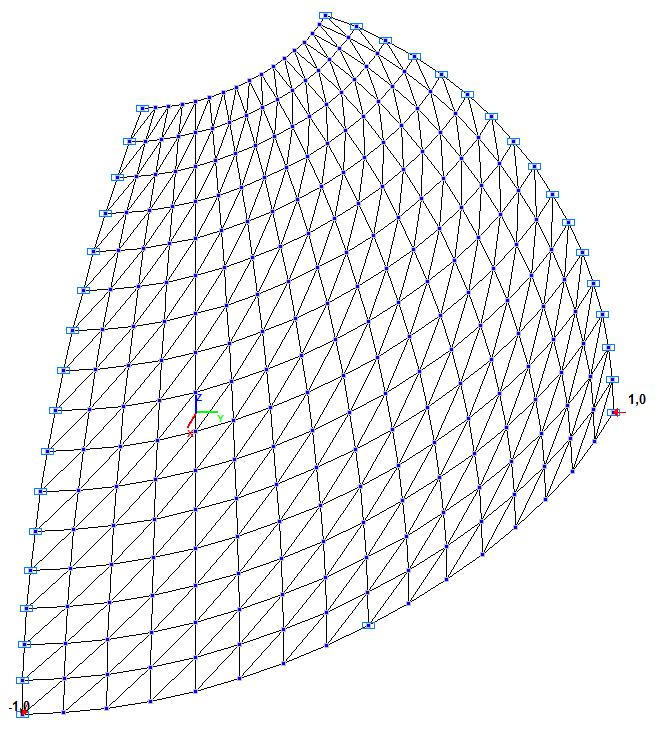
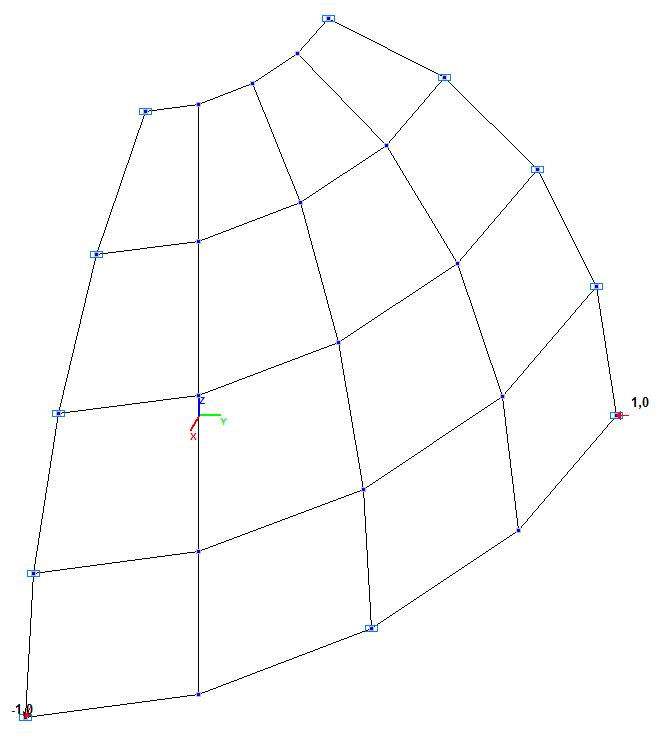
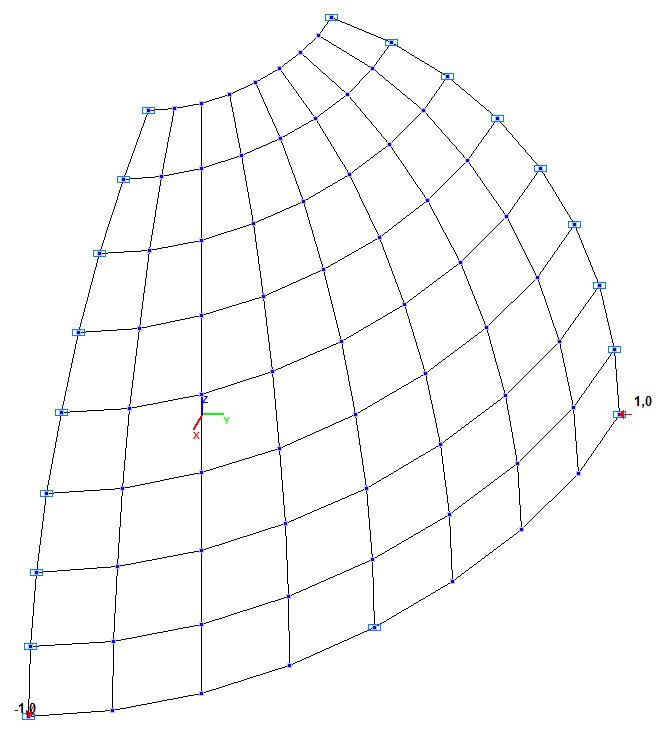
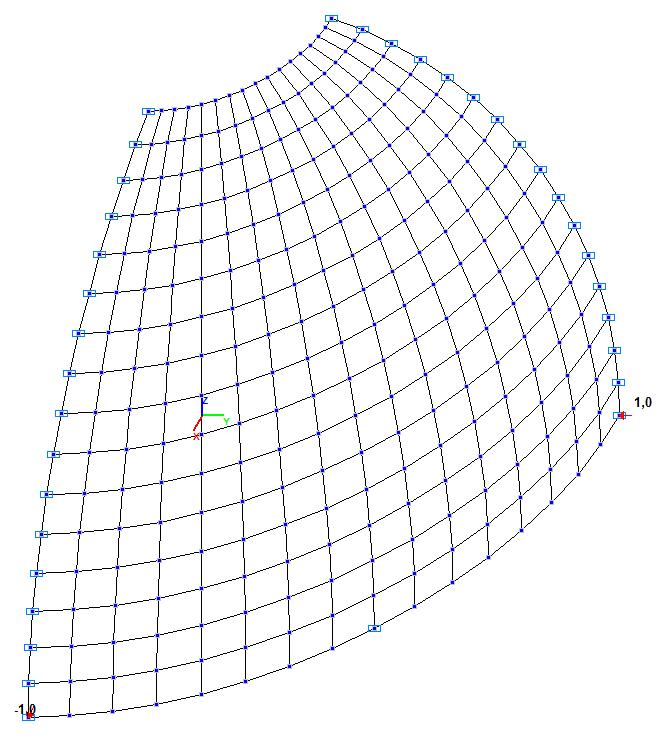
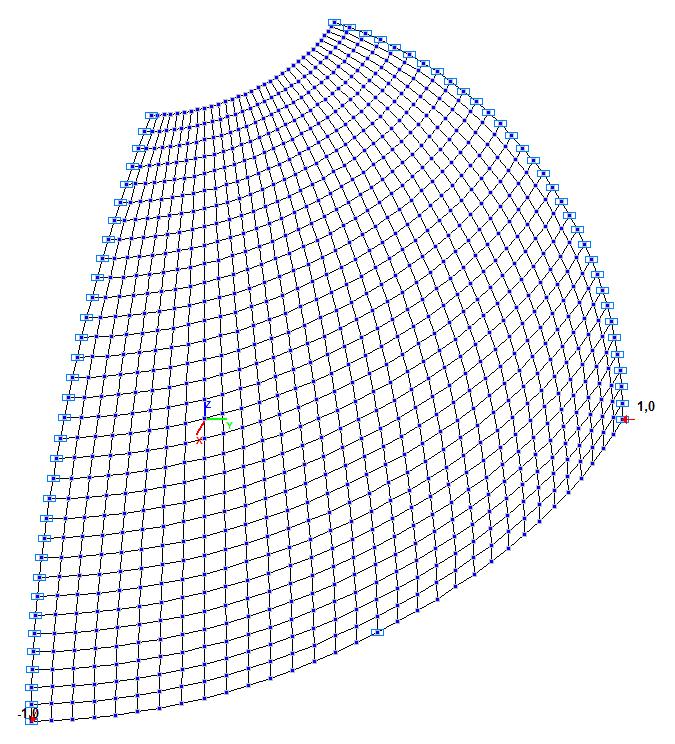
Модель 1. Расчетная схема

 




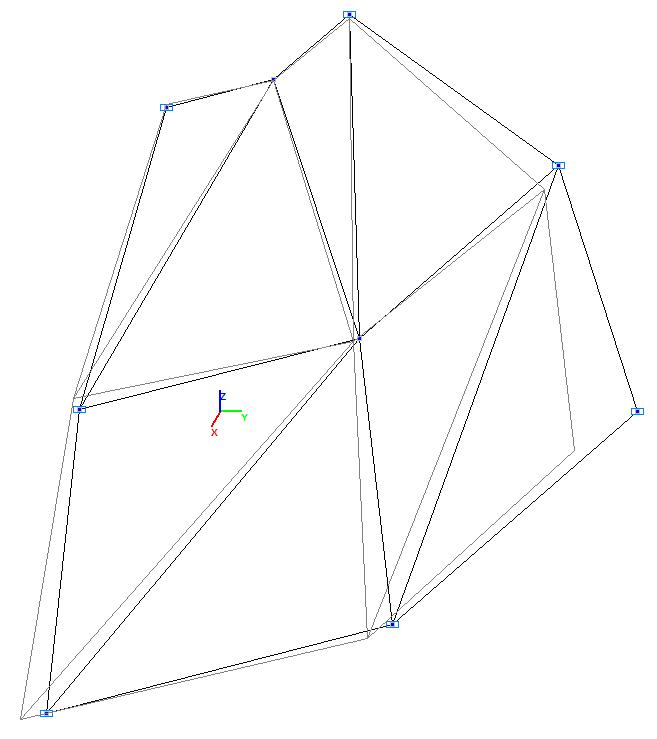
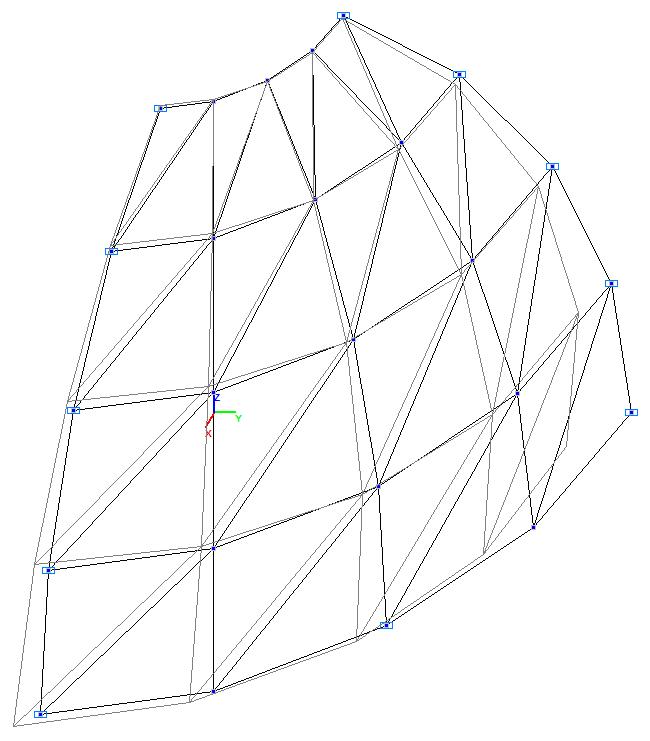
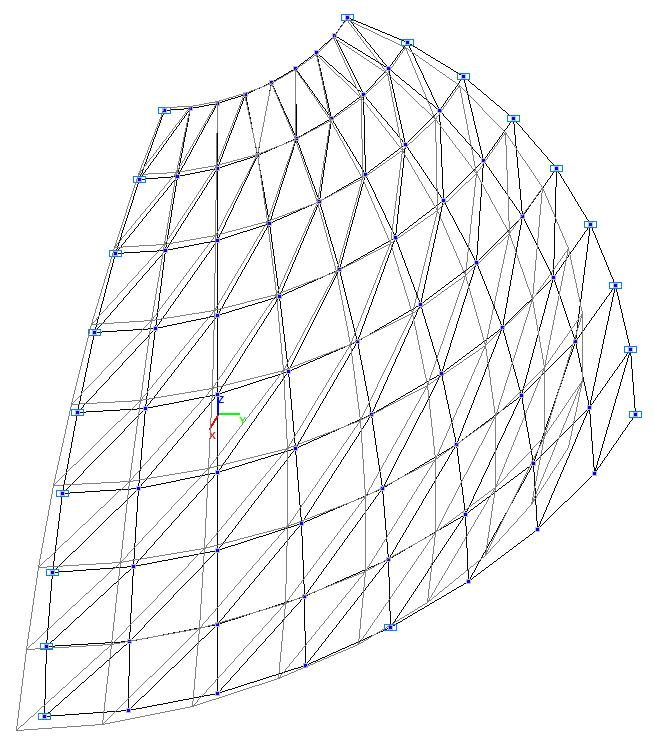
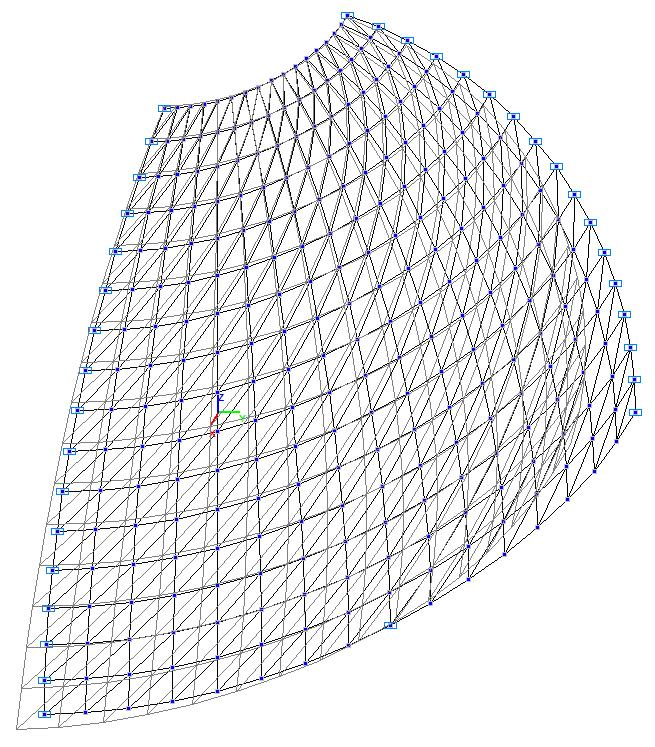
Модель 1. Деформированная схема

 











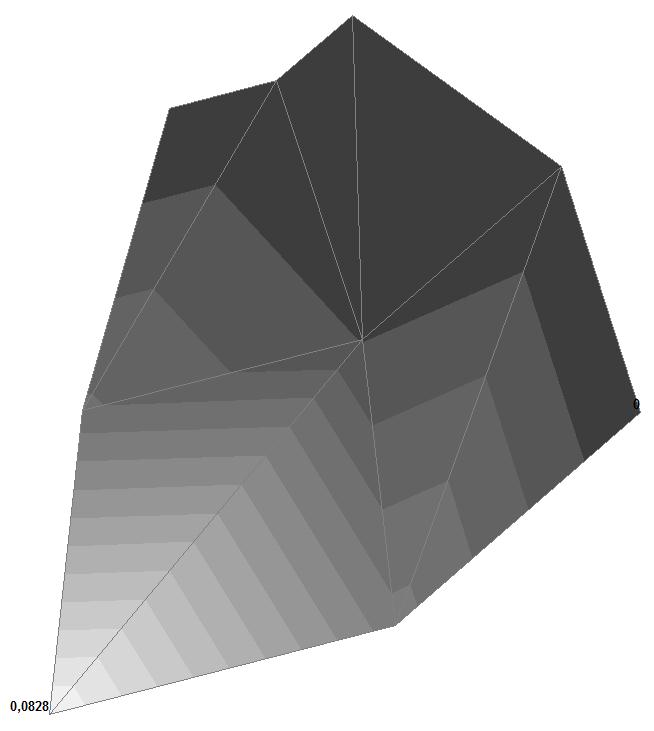
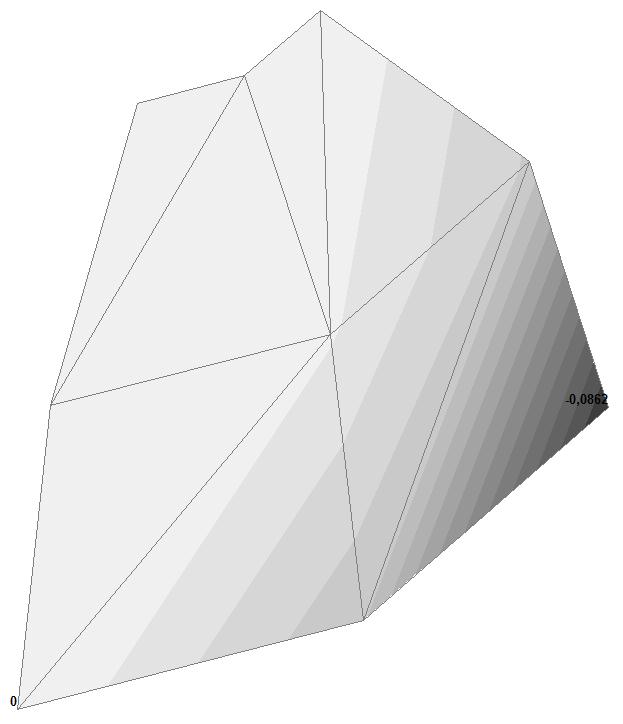
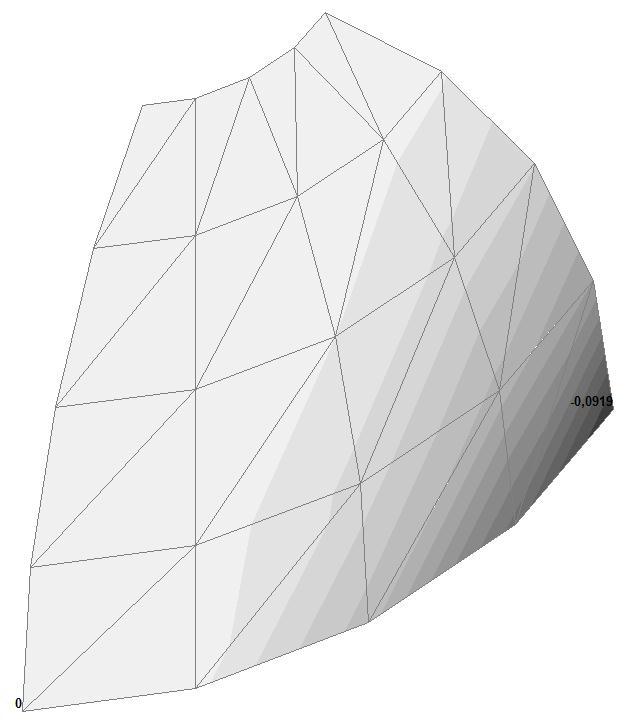
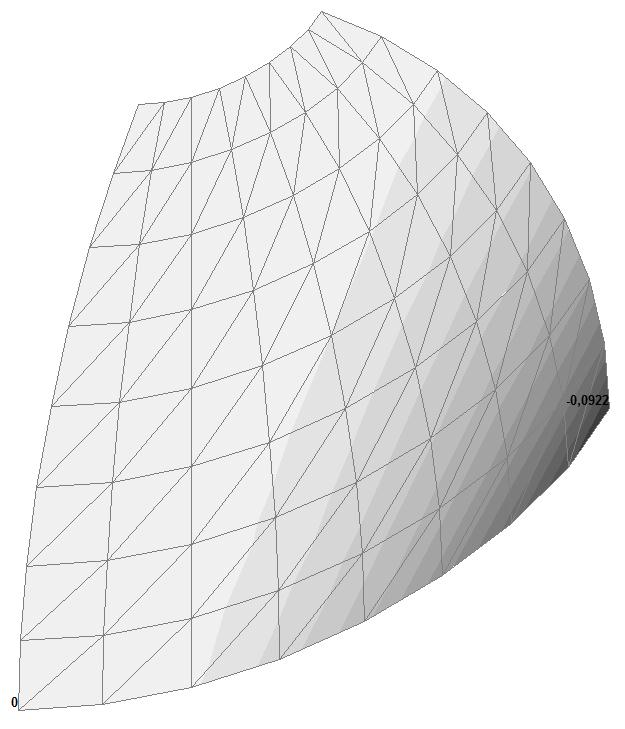
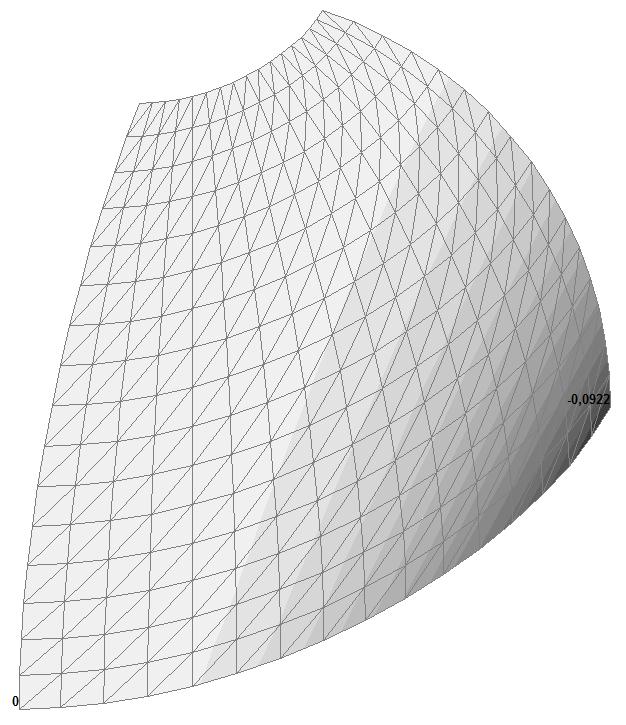
Модель 1. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

 



ScreenShot1685
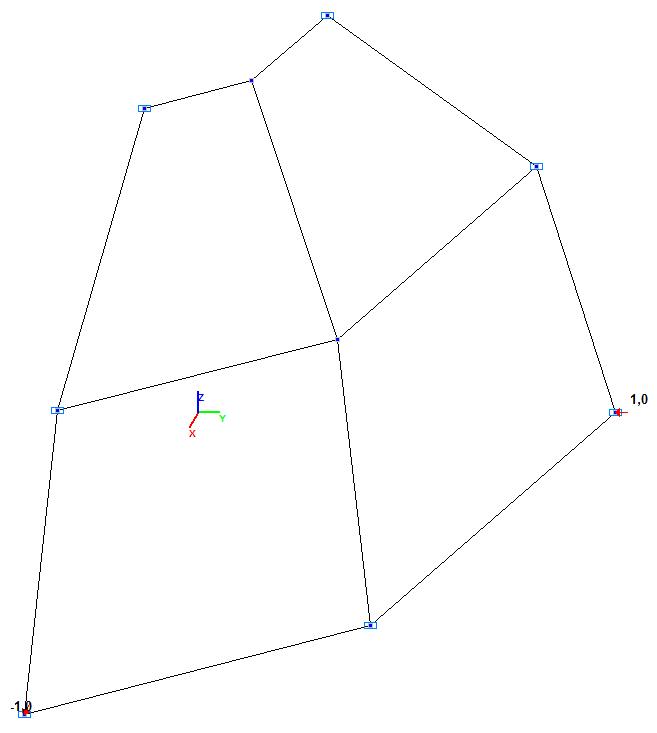
Модель 2. Расчетная схема

 




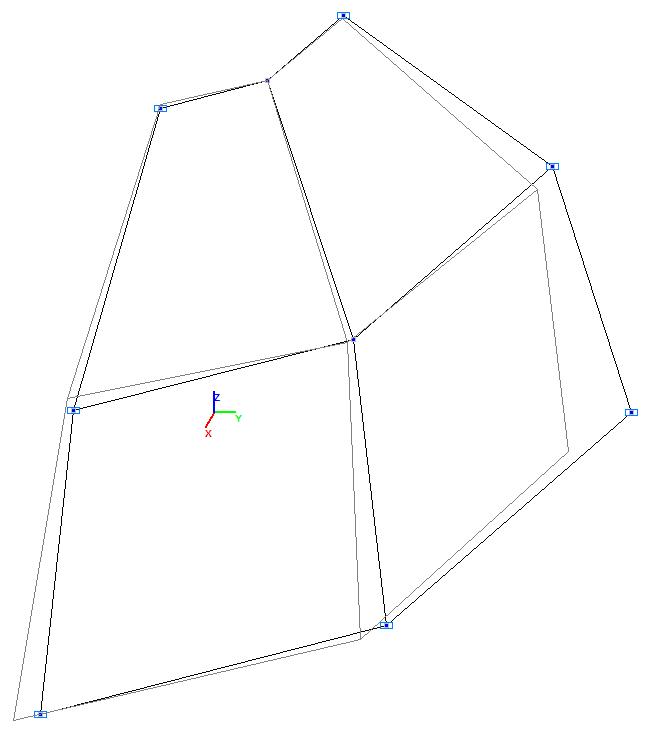
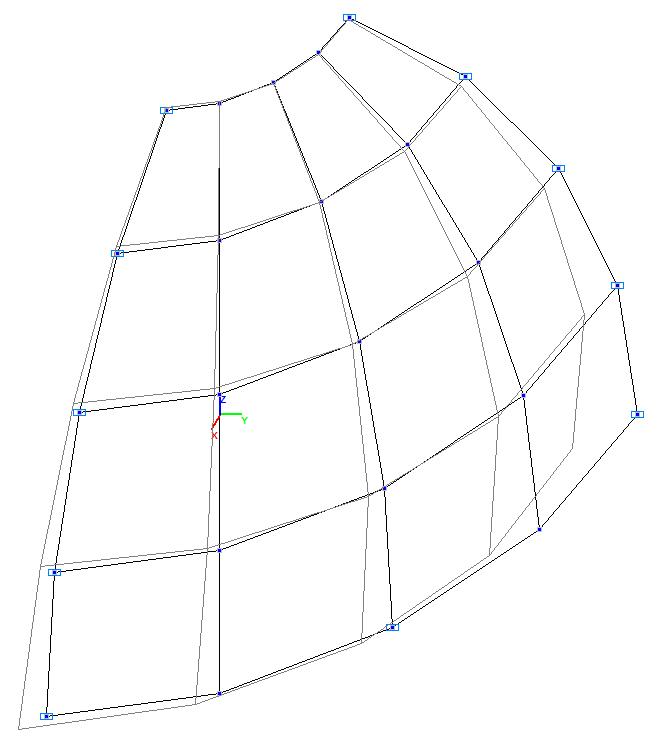
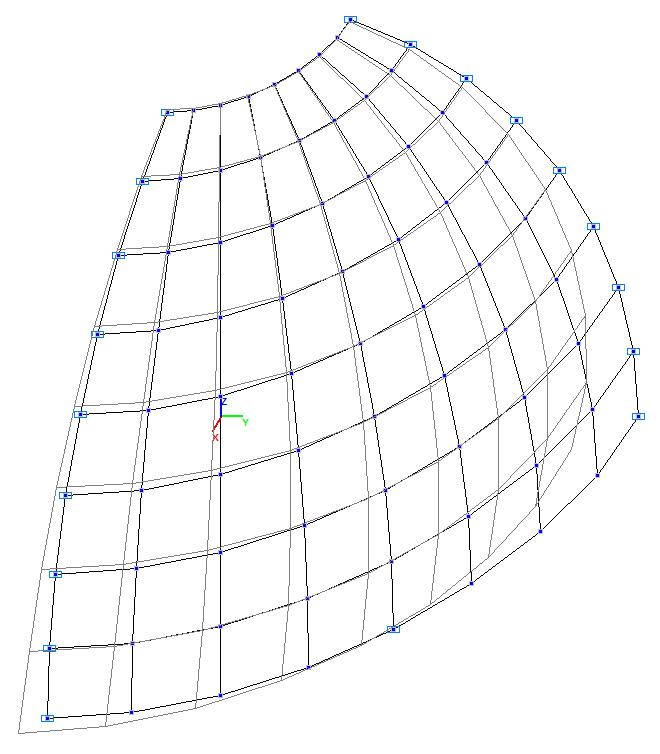
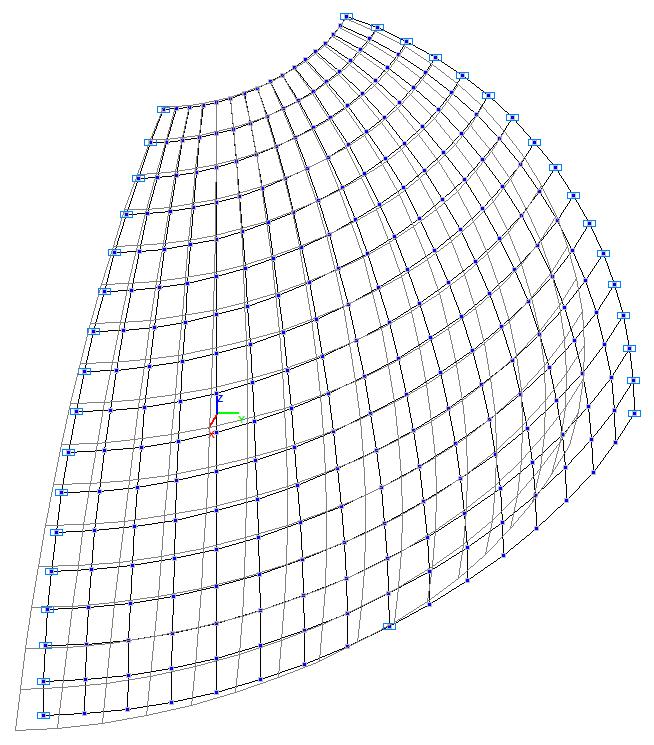
Модель 2. Деформированная схема

 











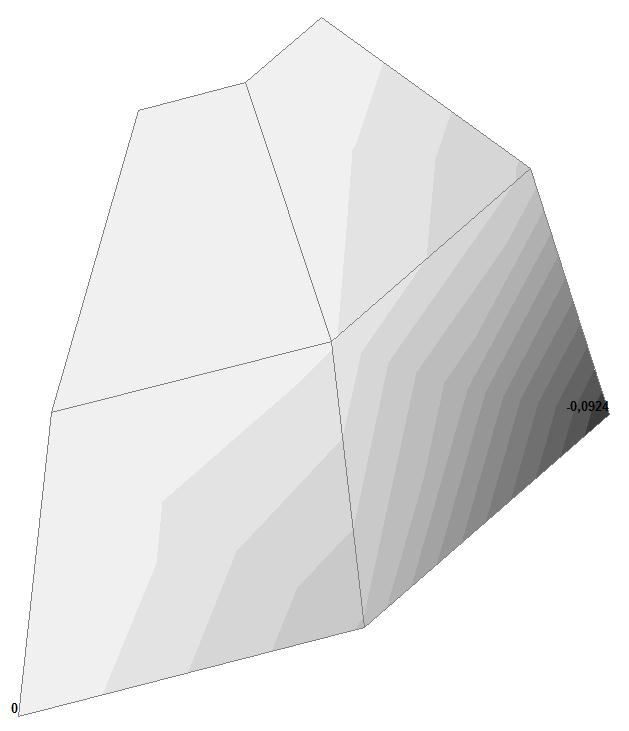
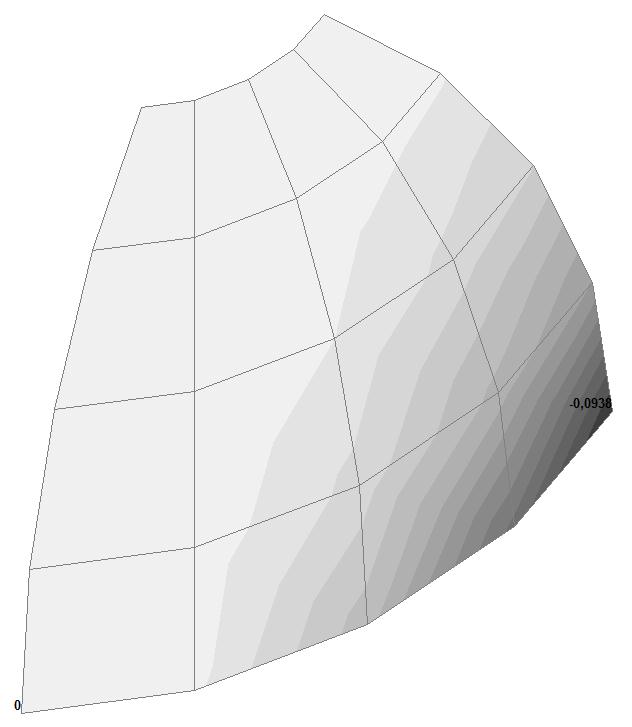
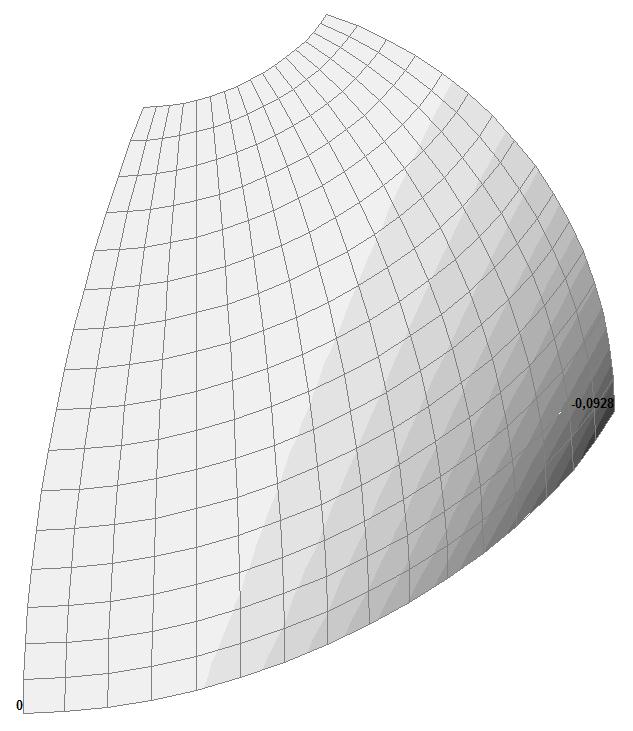
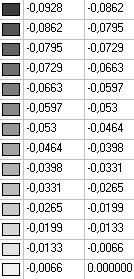
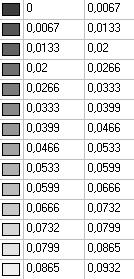
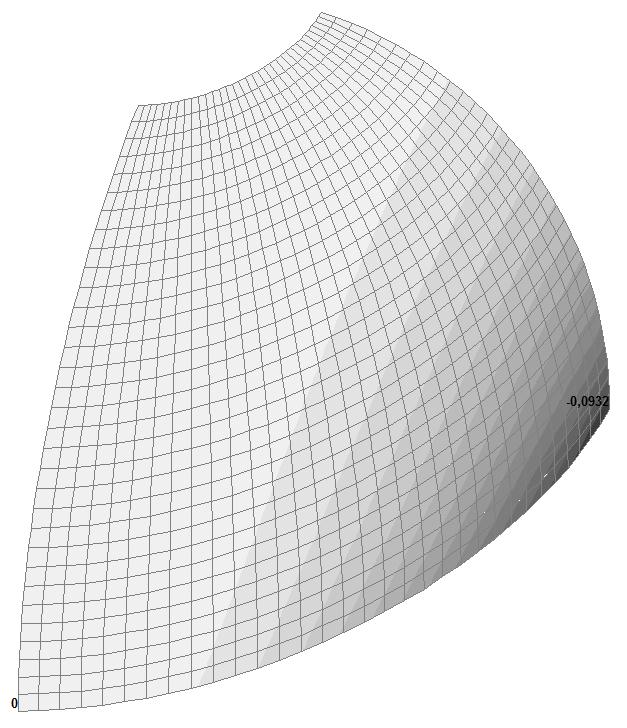
Модель 2. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

 




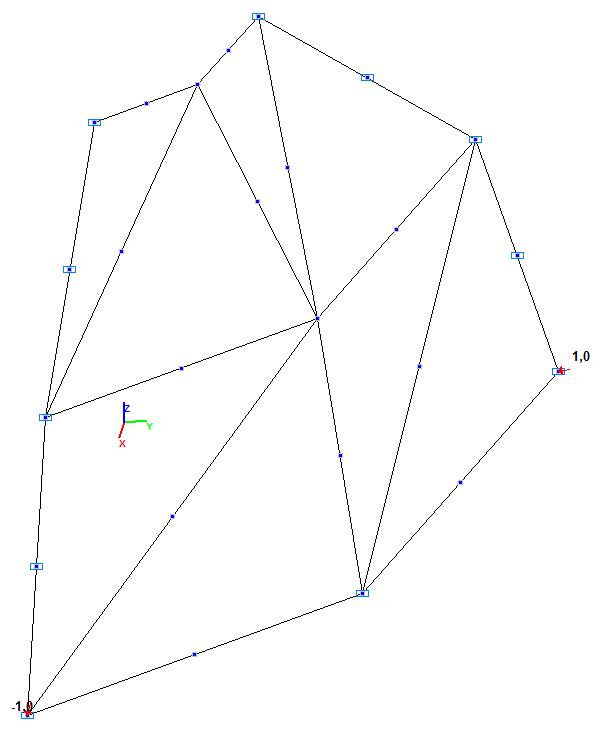
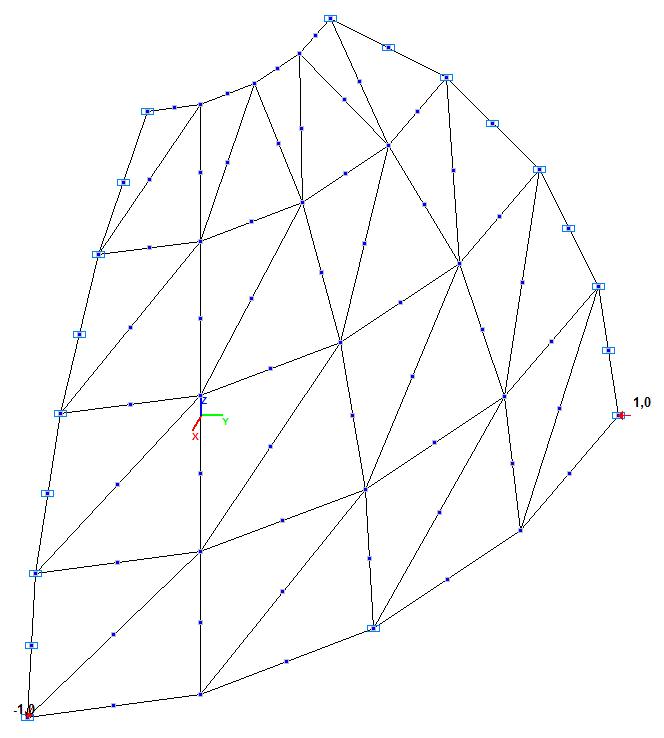
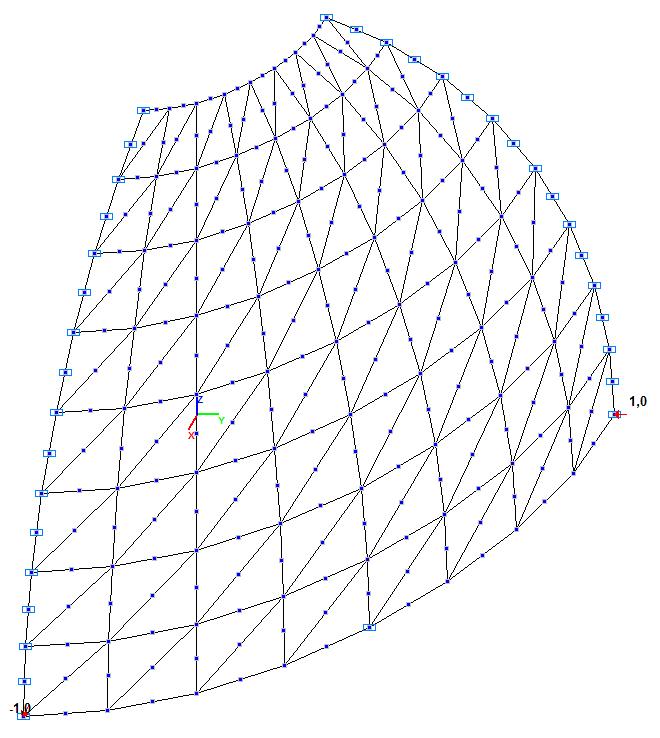
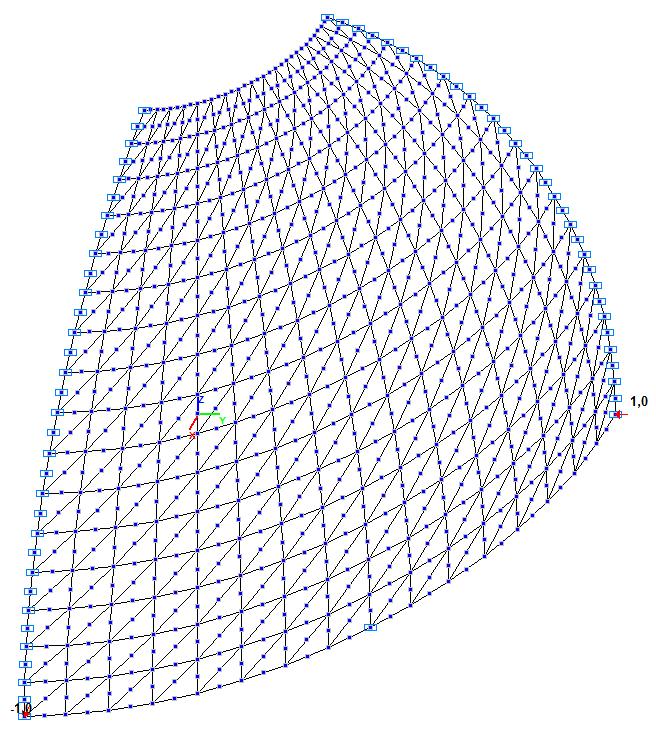
Модель 3. Расчетная схема

 




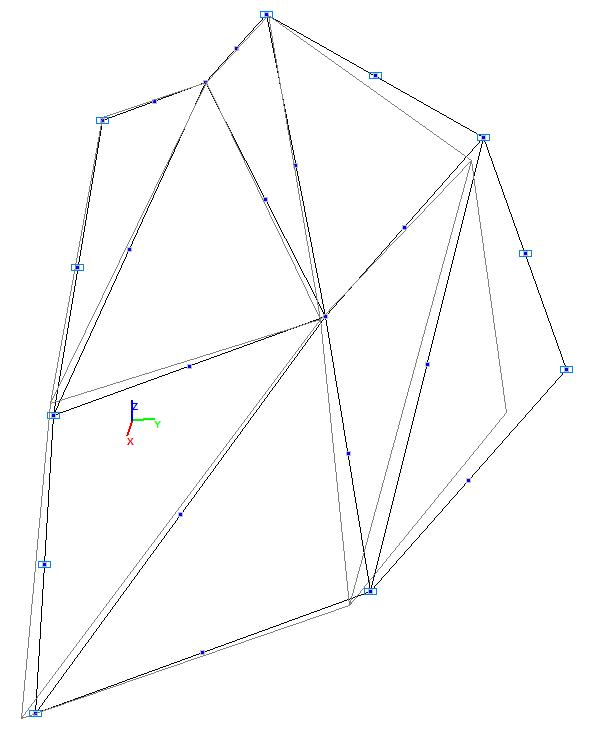
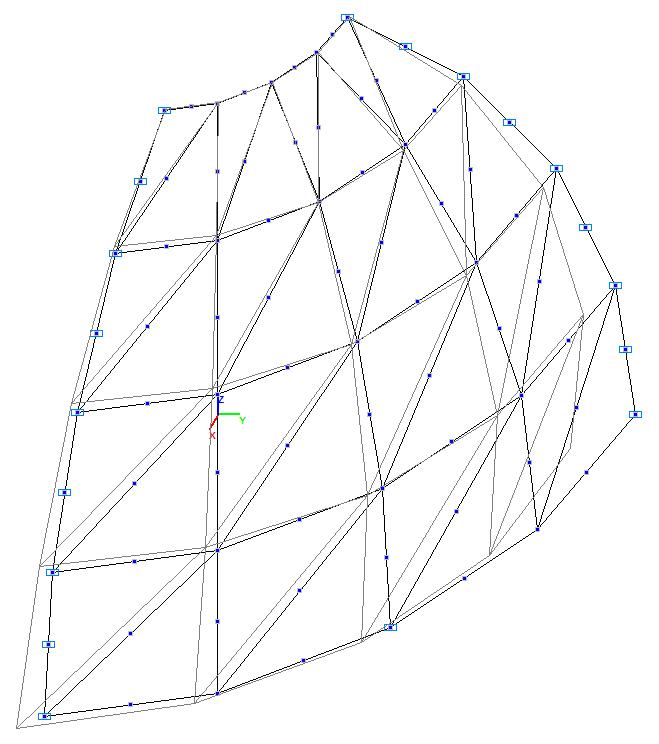
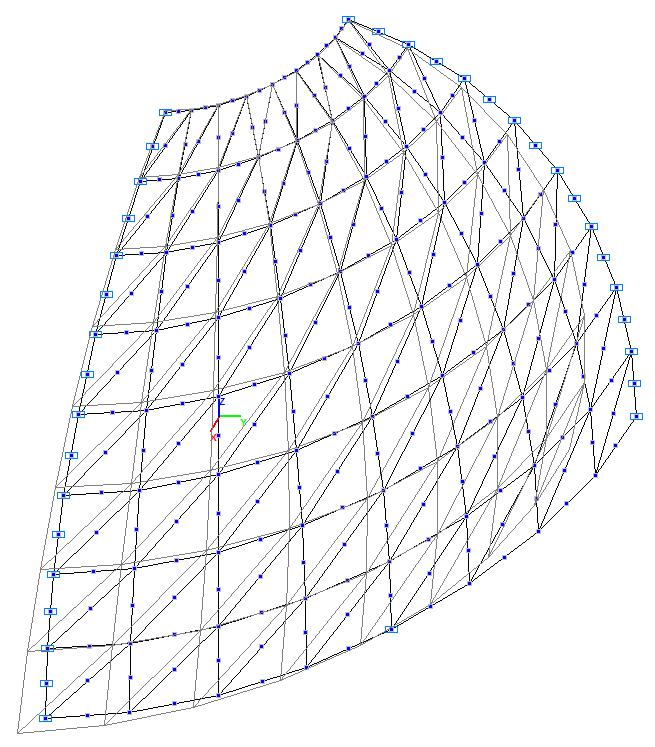
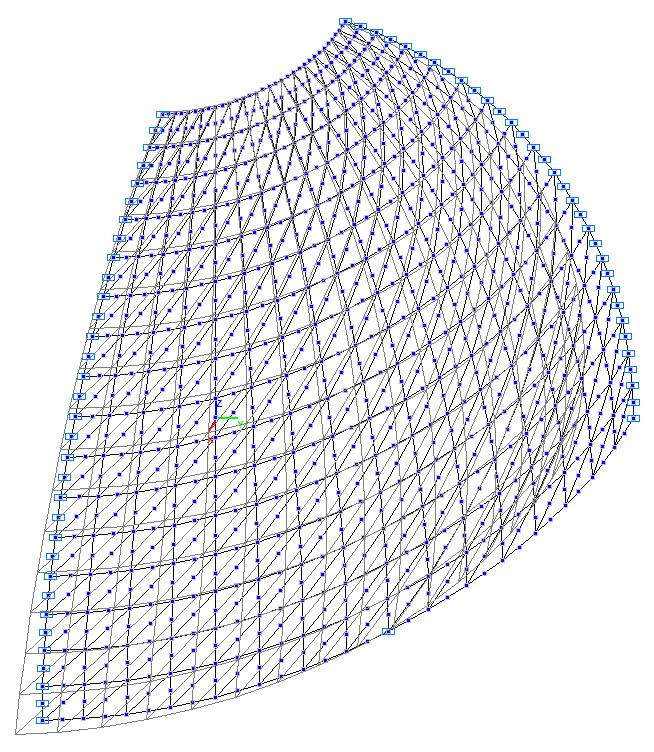
Модель 3. Деформированная схема

 











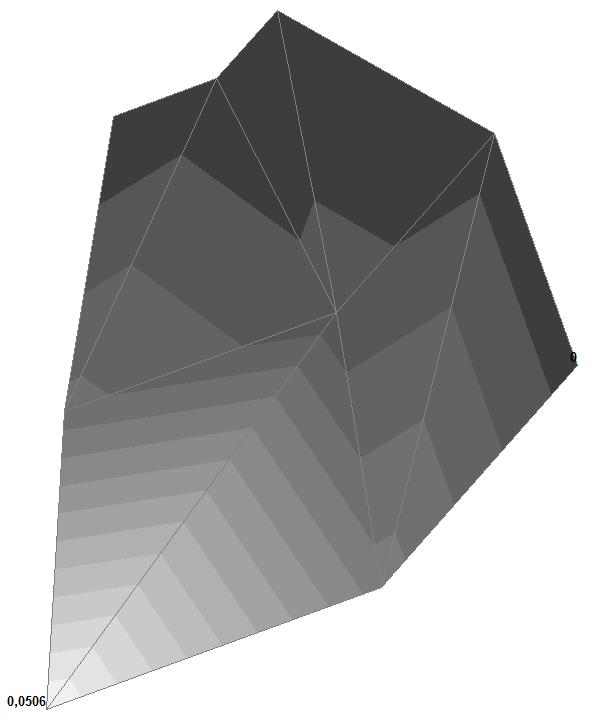
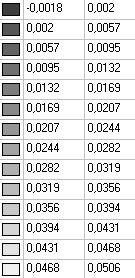
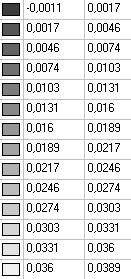
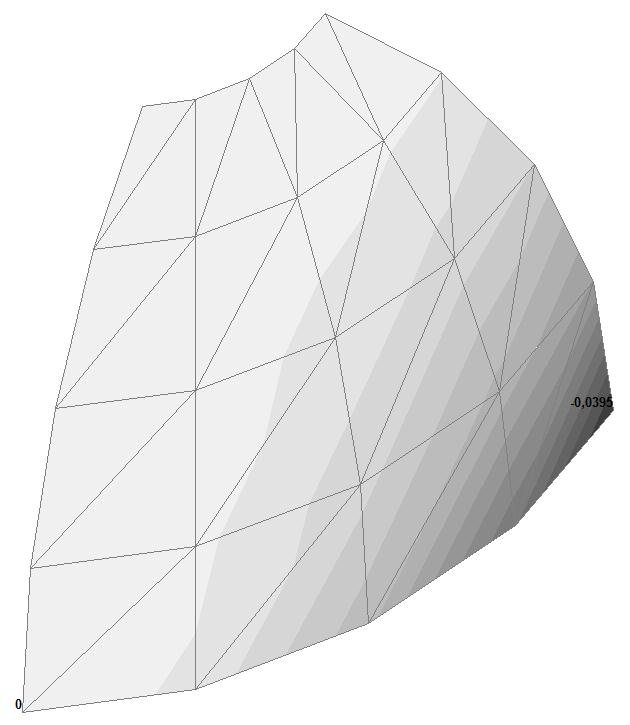
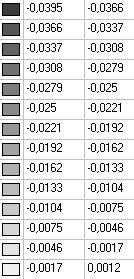
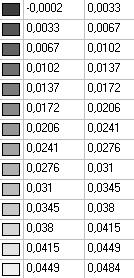
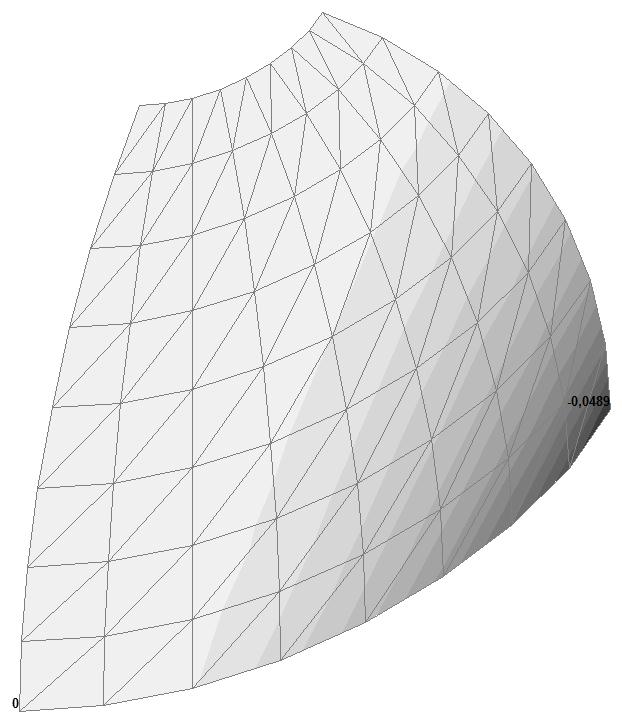
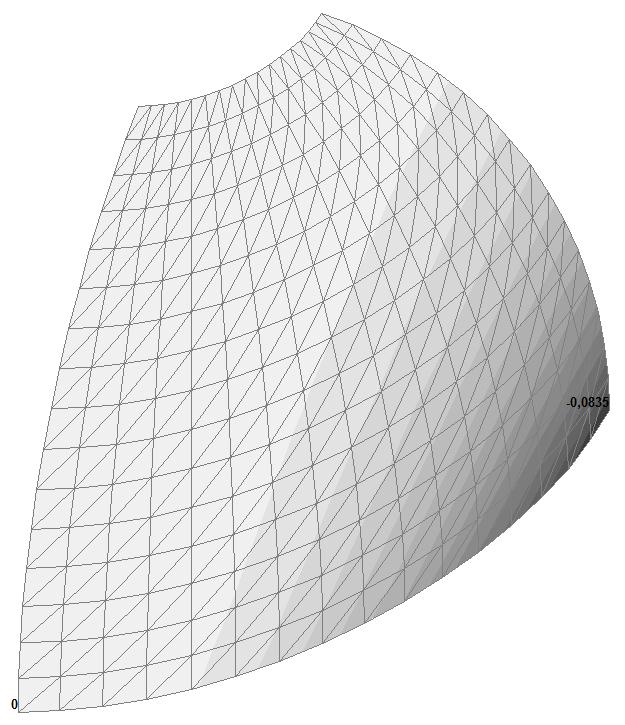
Модель 3. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

 




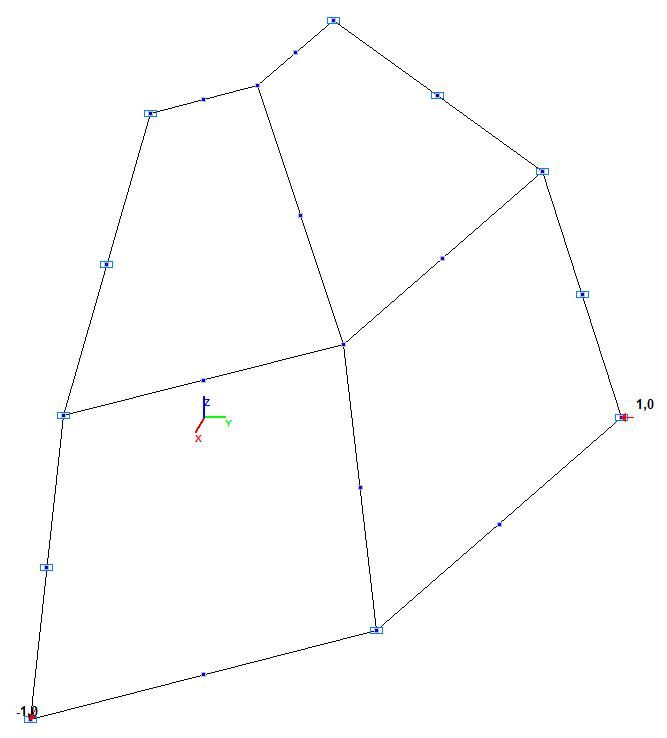
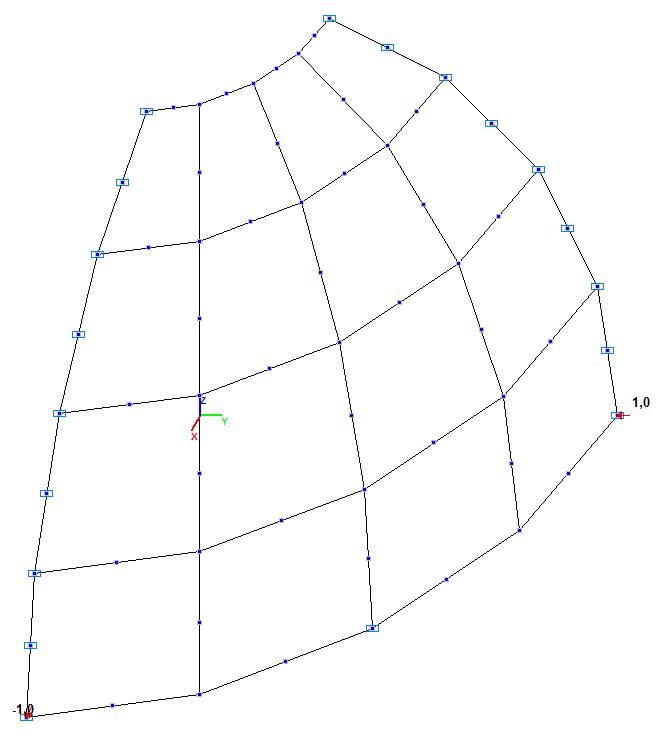
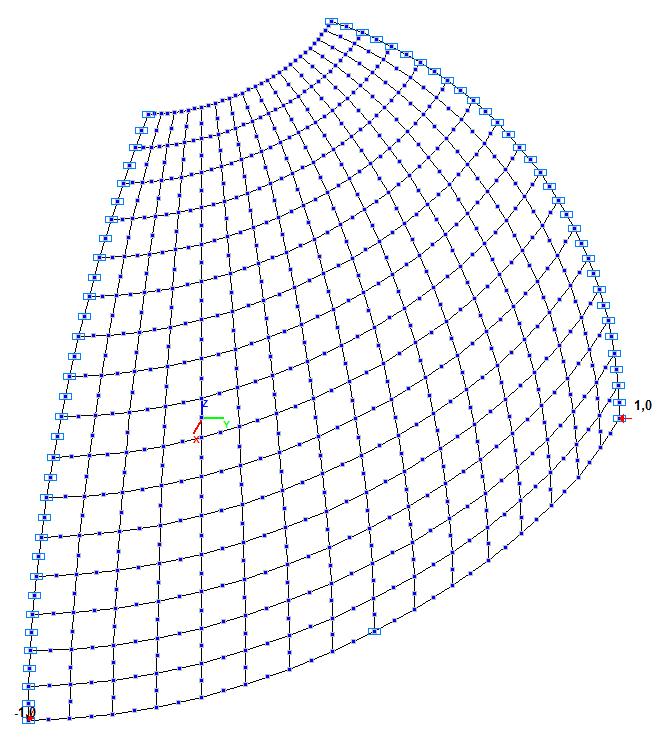
Модель 4. Расчетная схема

 




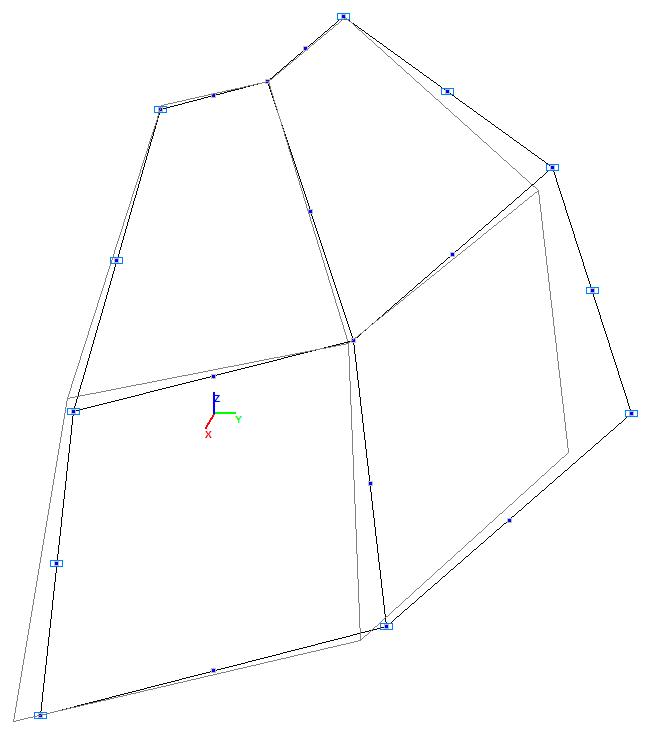
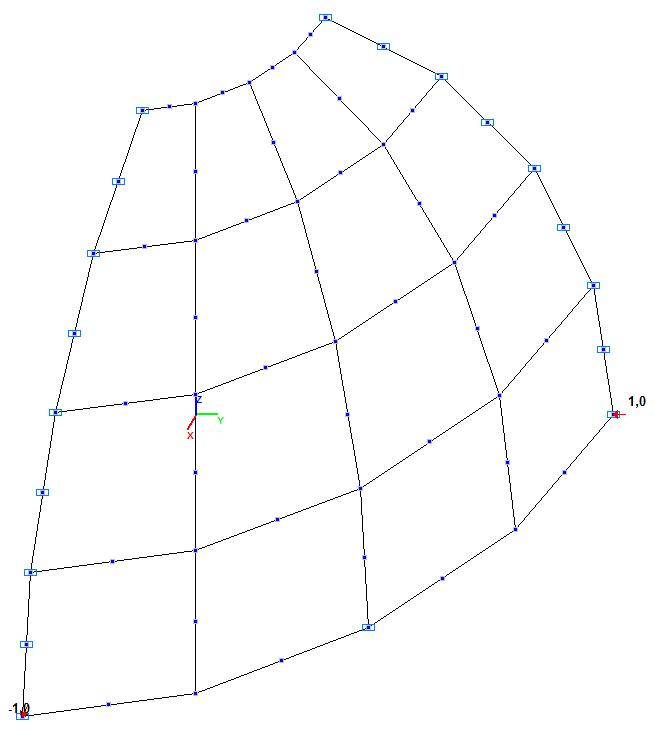
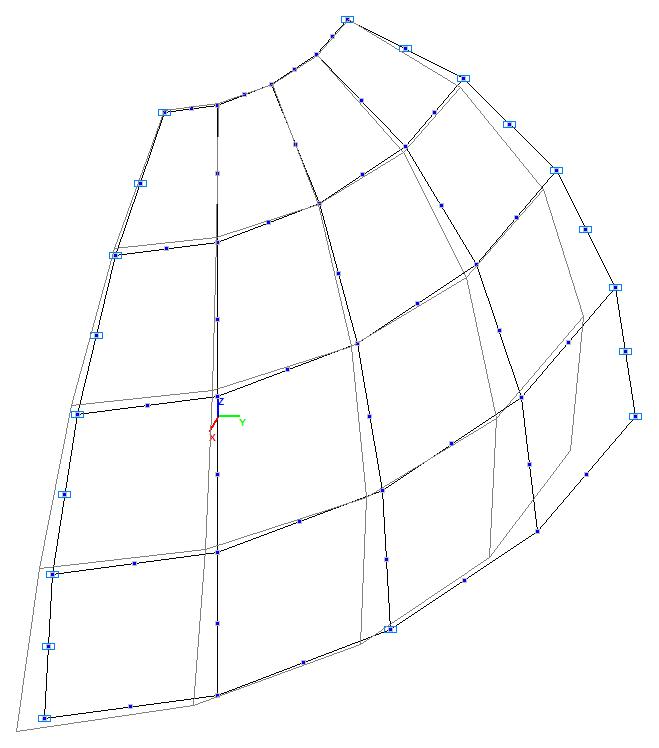
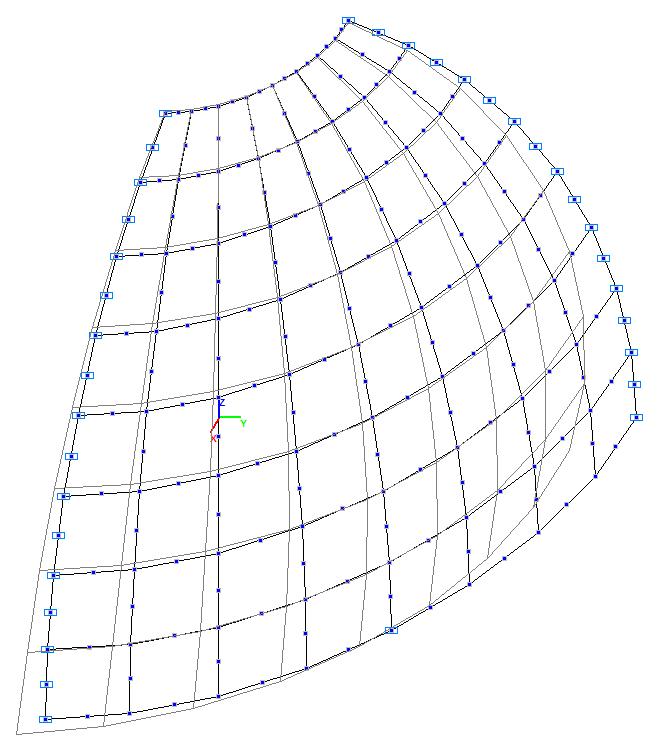
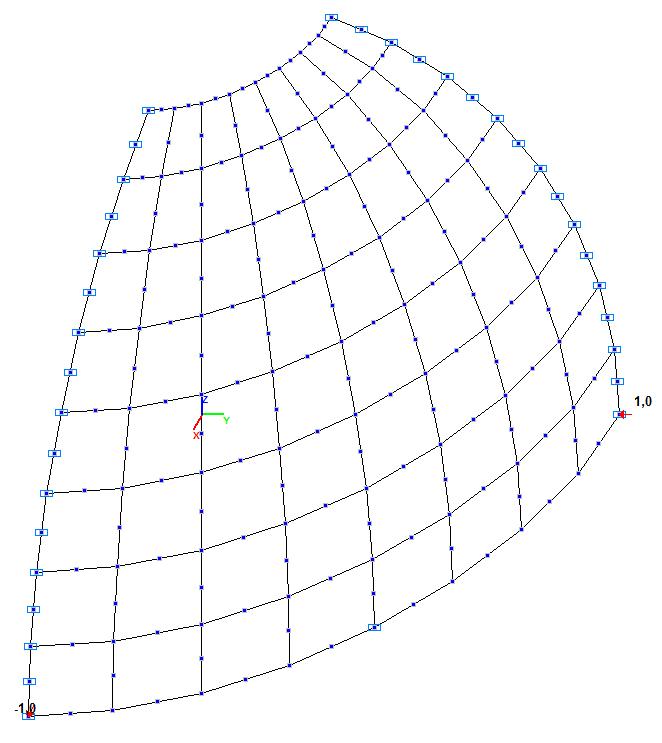
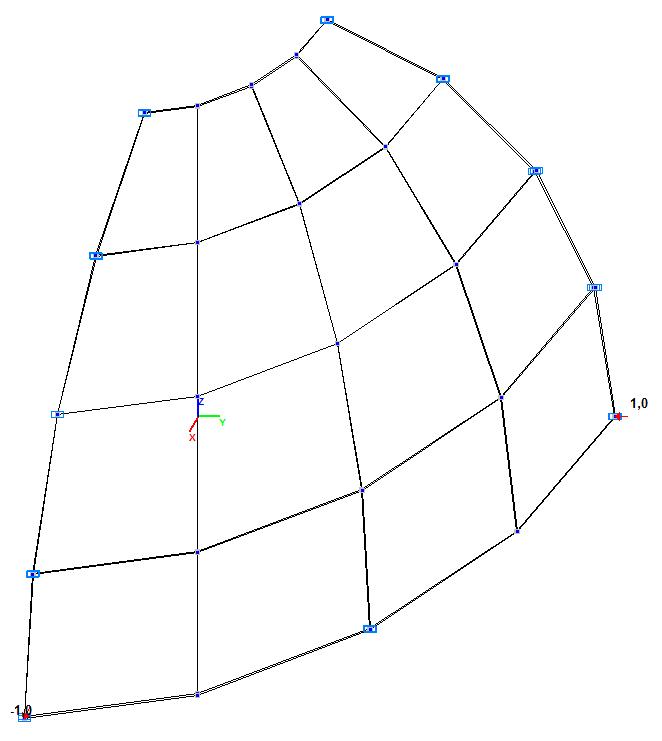
Модель 4. Деформированная схема

 











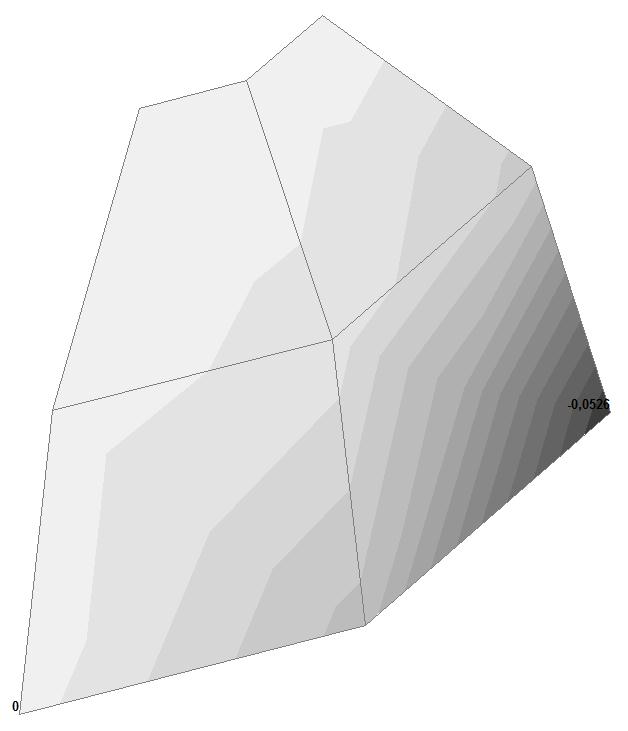
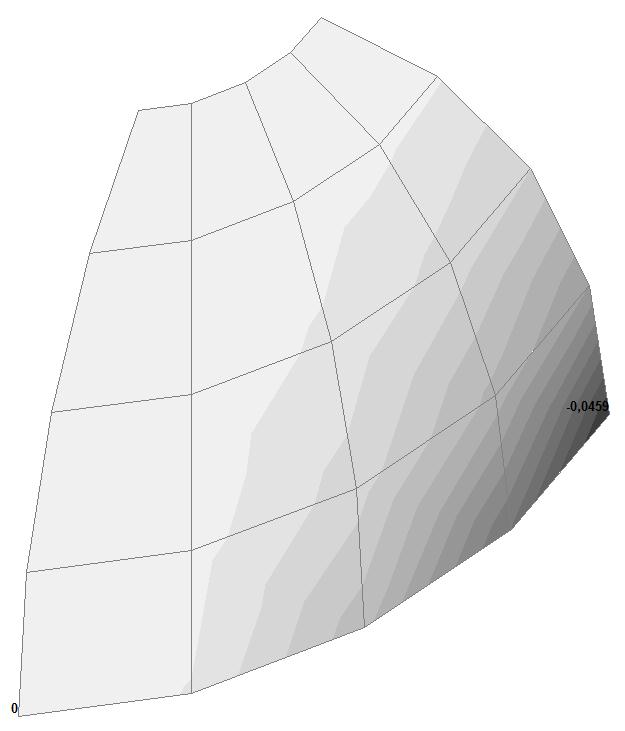
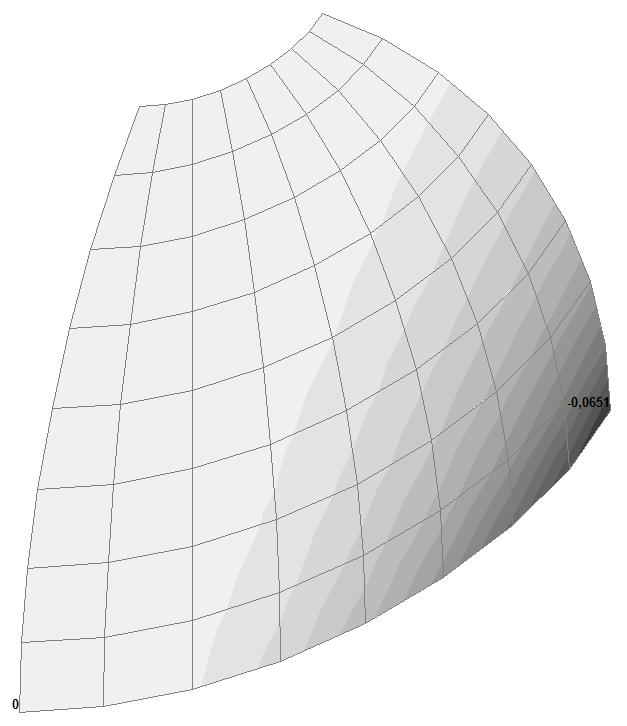
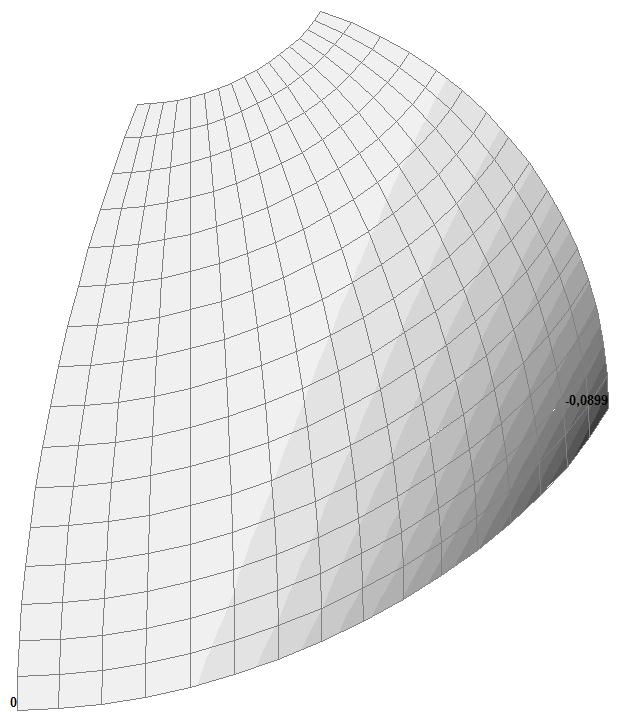
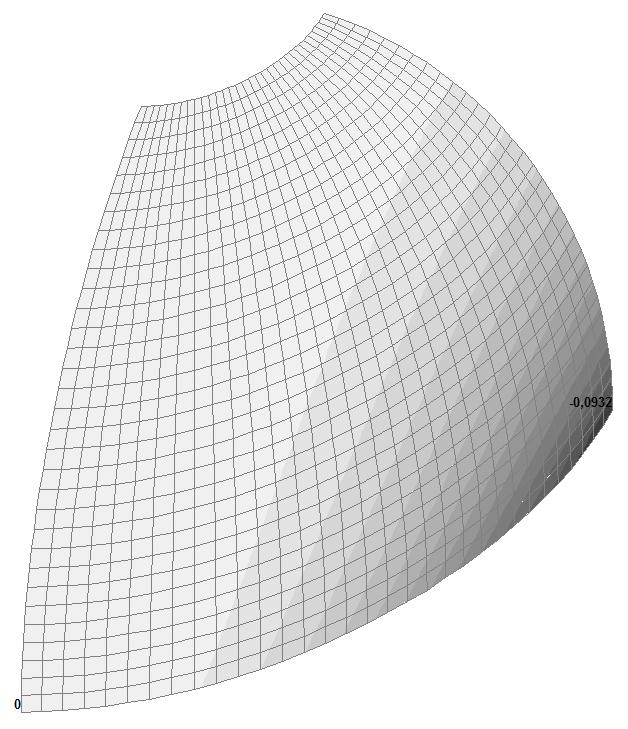
Модель 4. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

 






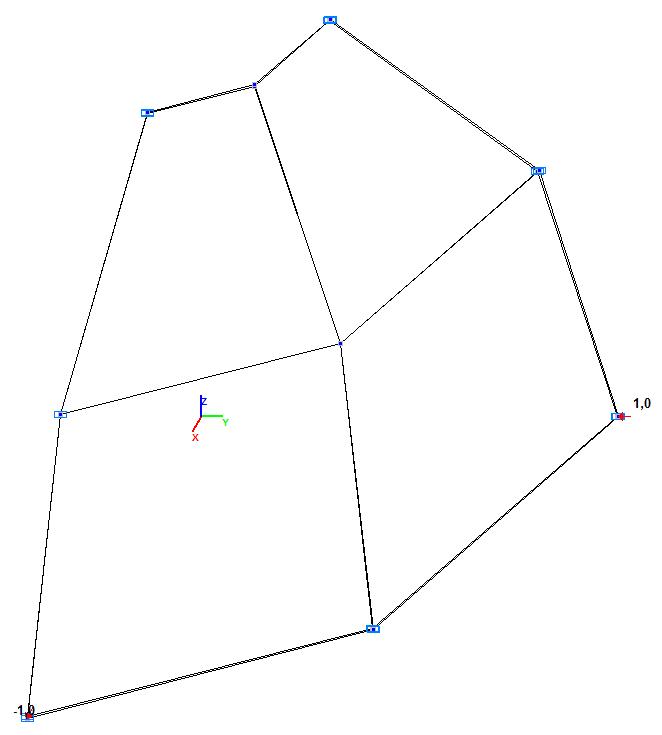
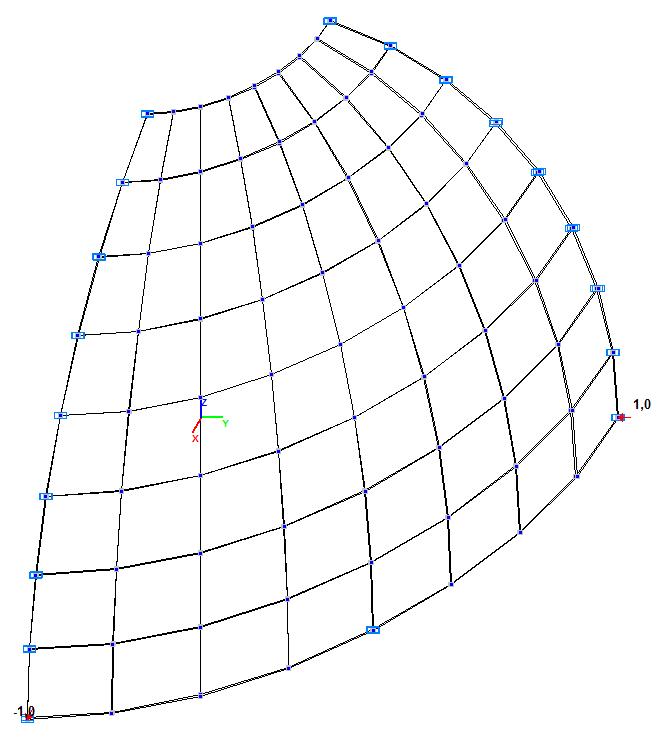
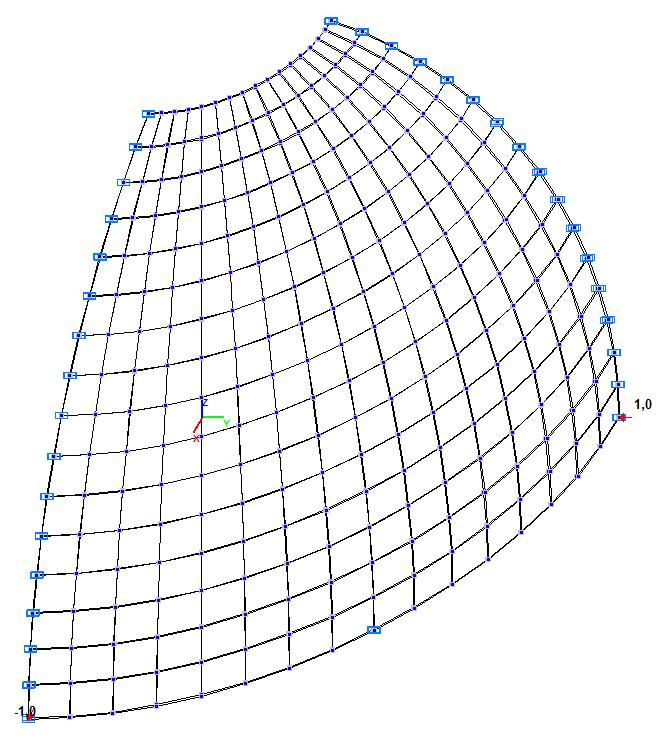
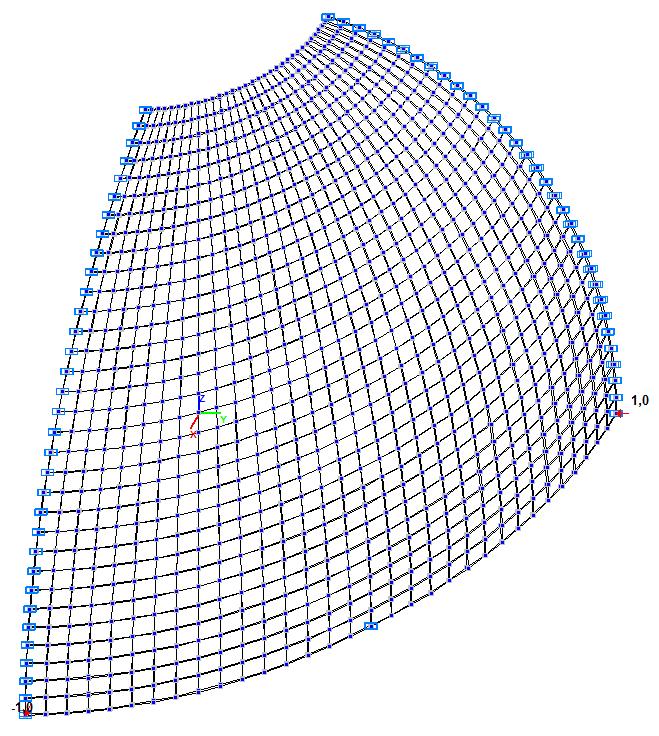
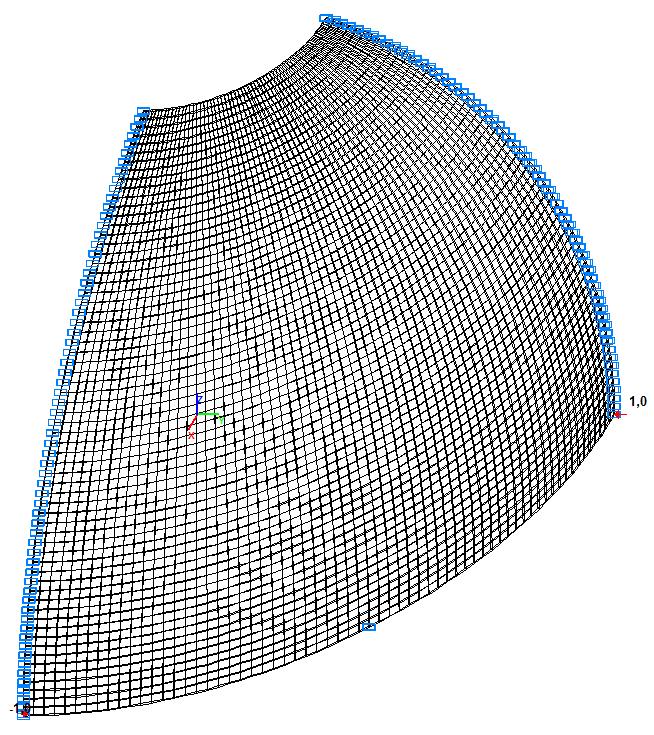
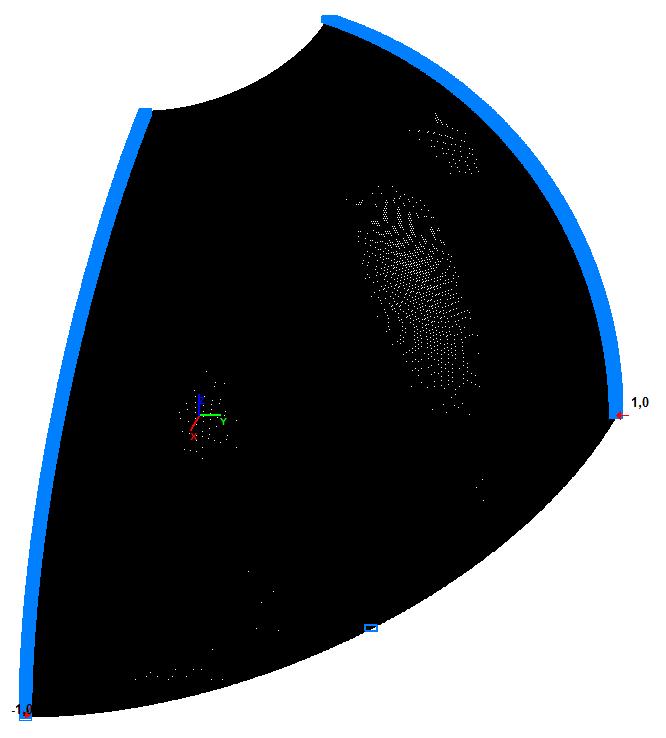
Модель 5. Расчетная схема

 






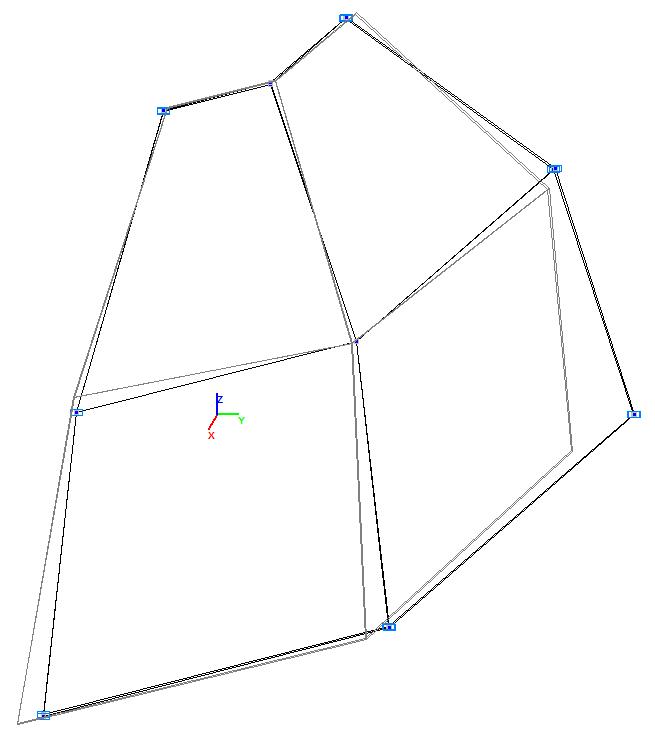
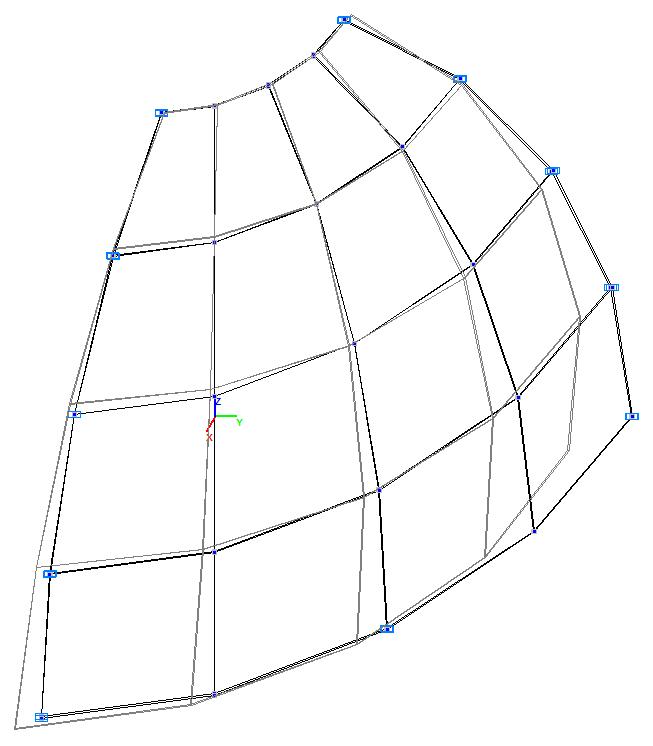
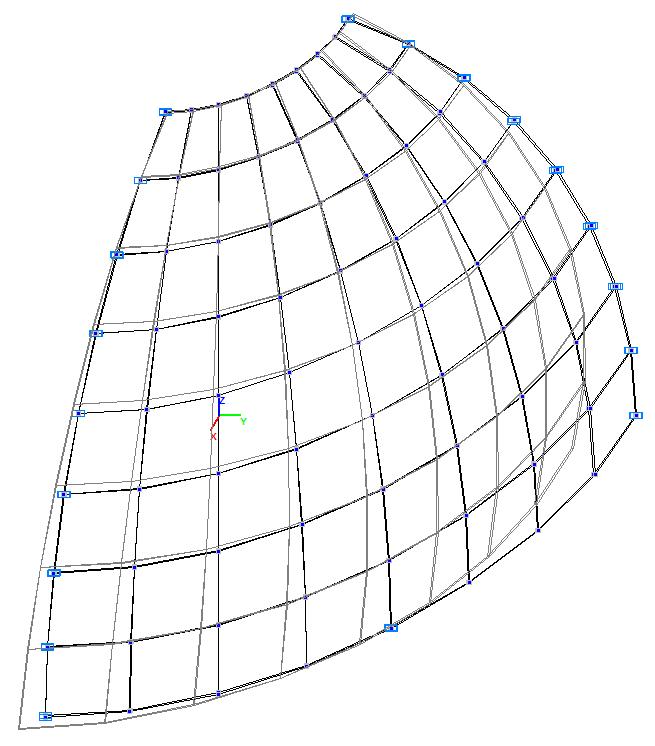
Модель 5. Деформированная схема

 

















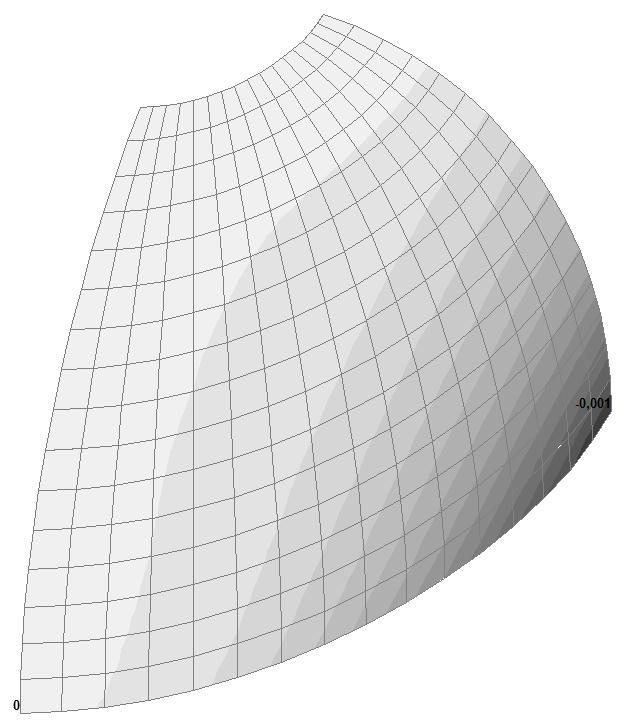
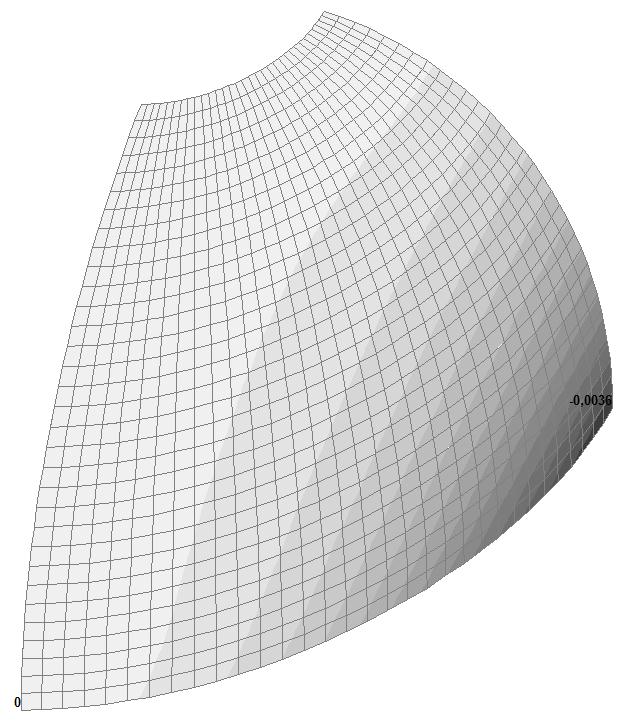
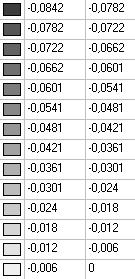
Модель 5. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

 





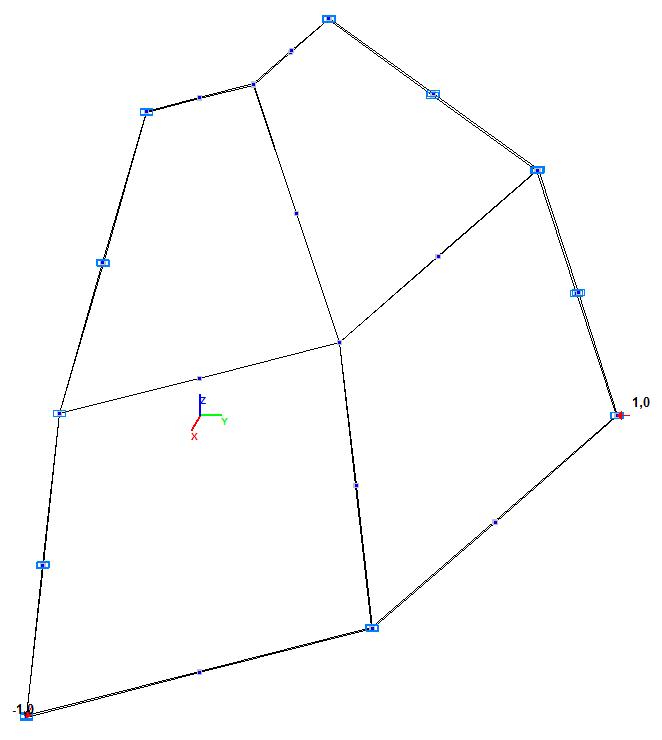
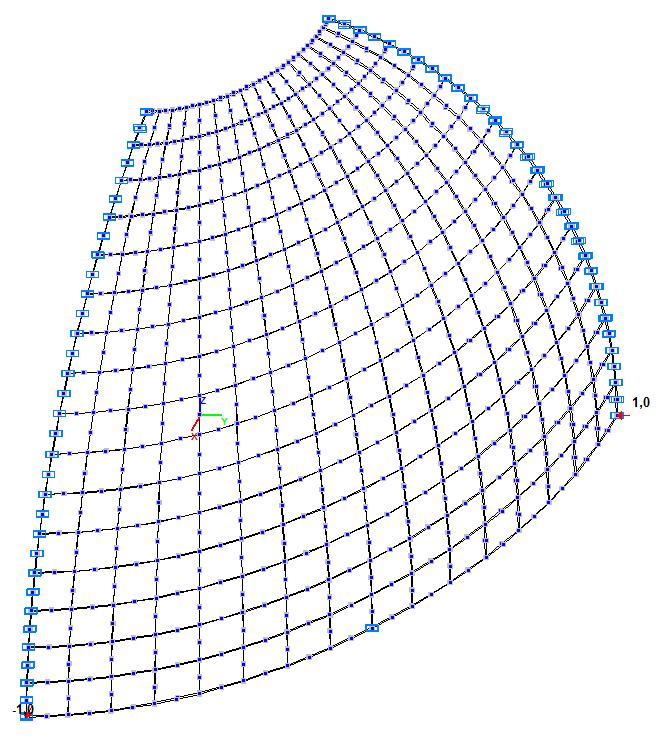
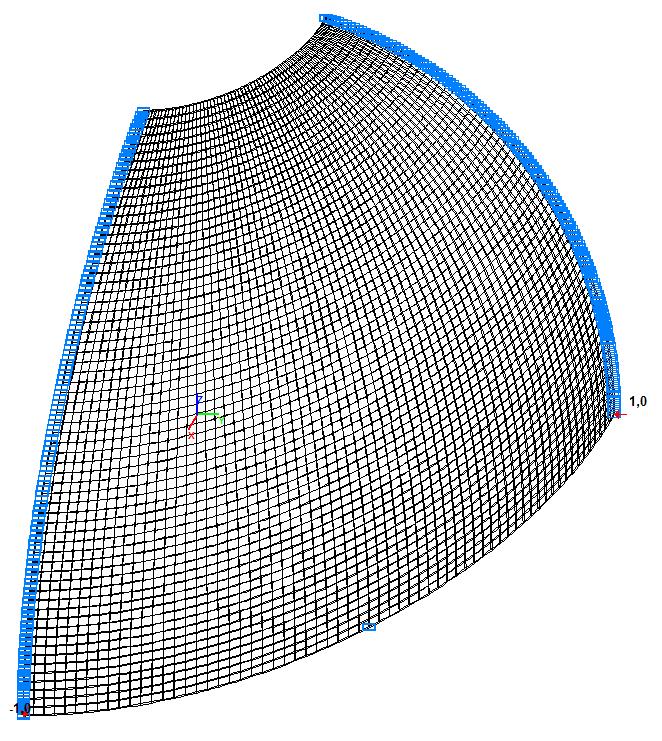
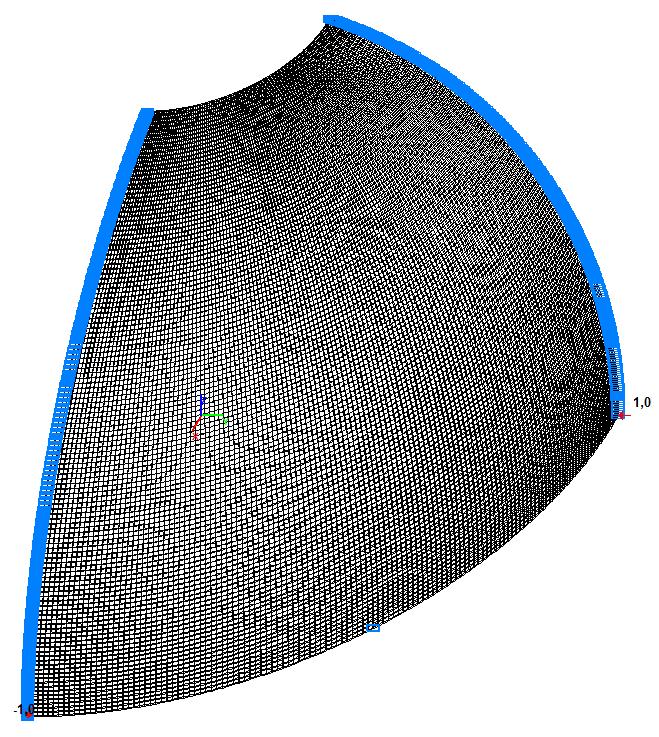
Модель 6. Расчетная схема

 





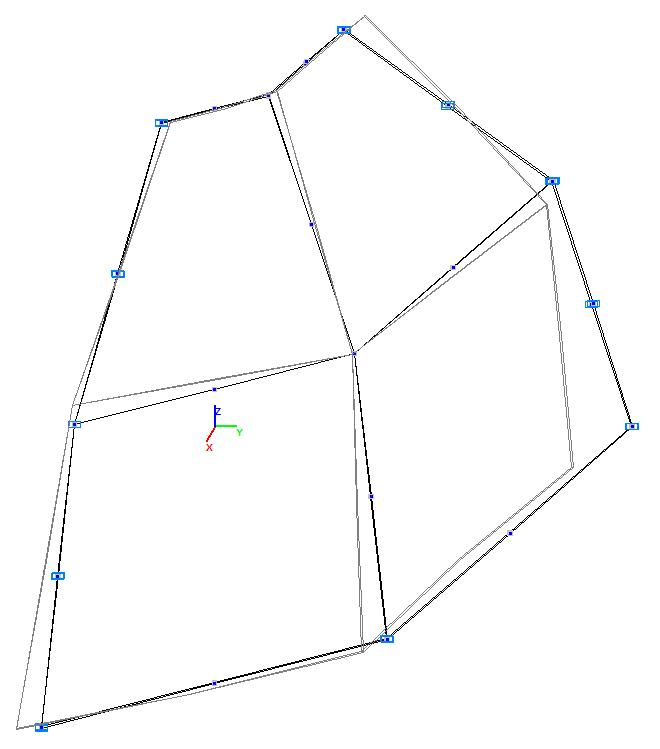
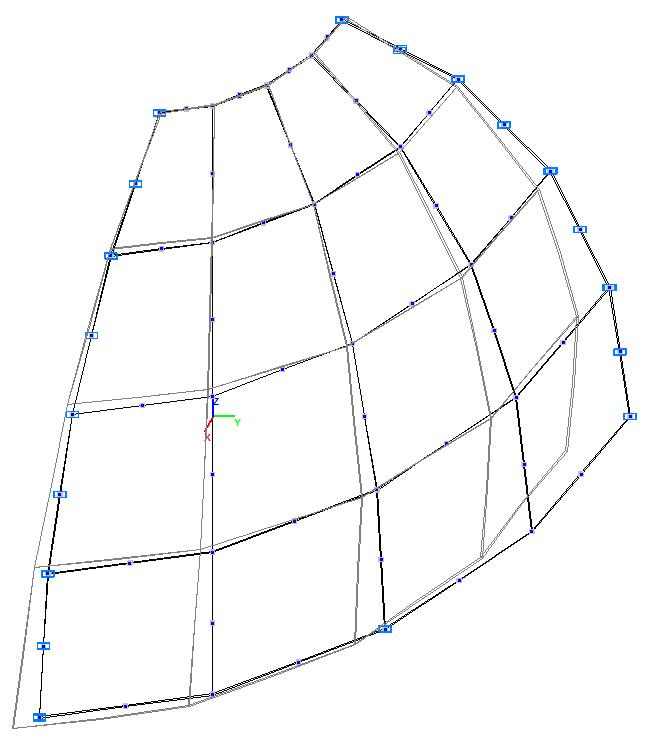
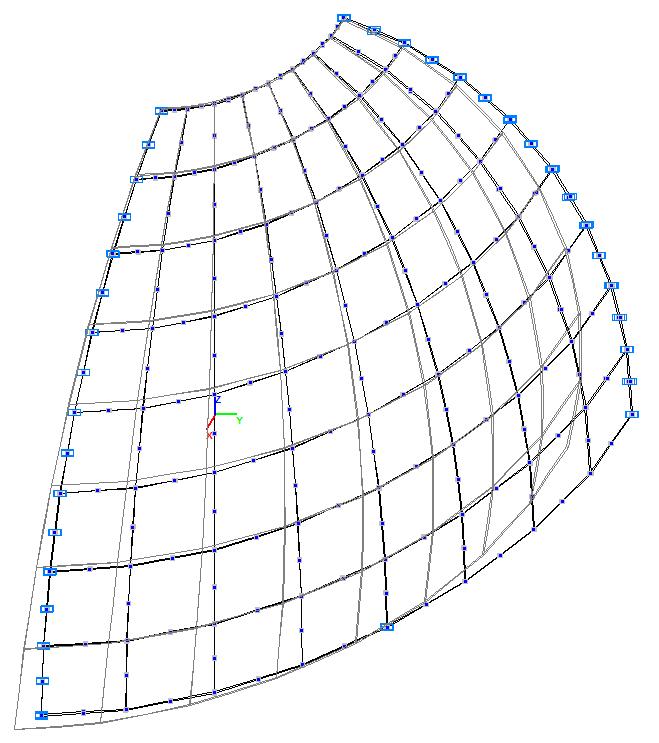
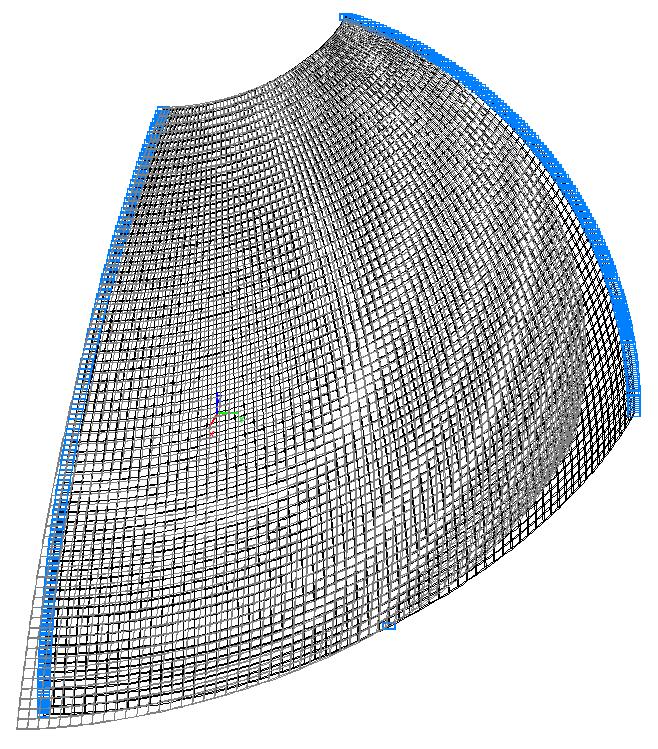
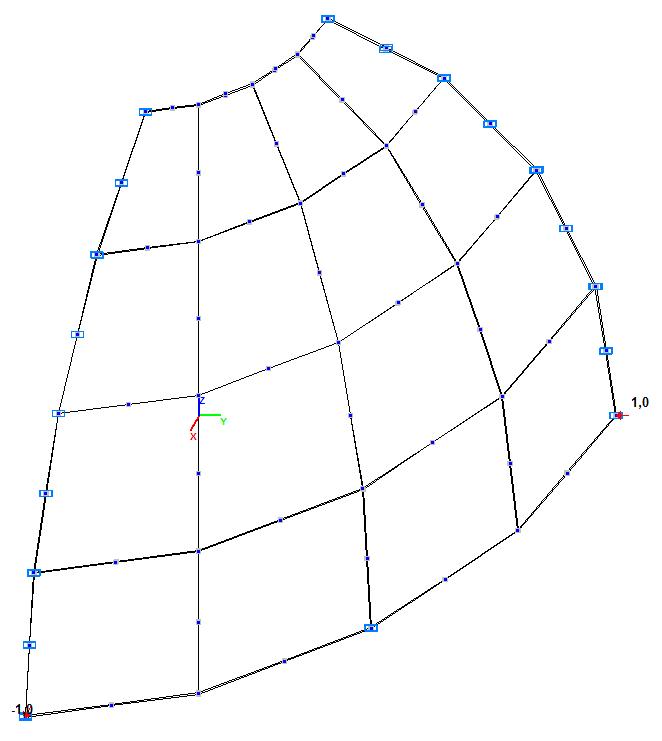
Модель 6. Деформированная схема

 















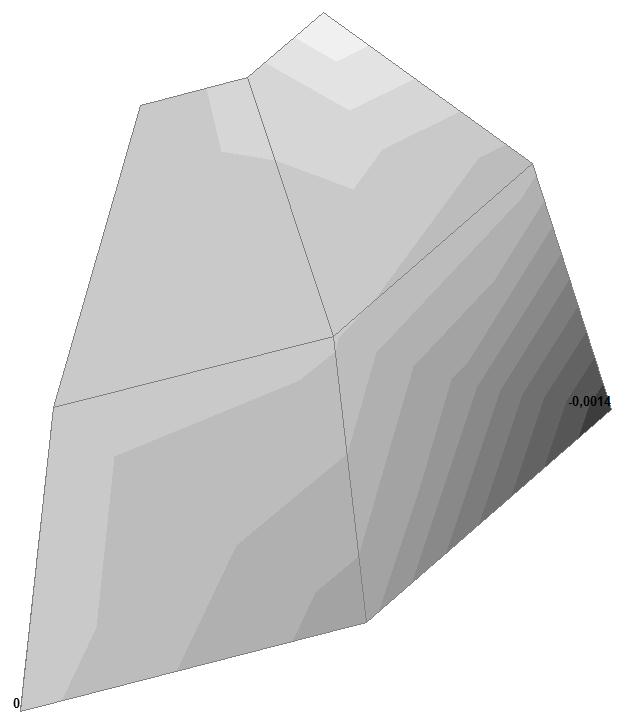
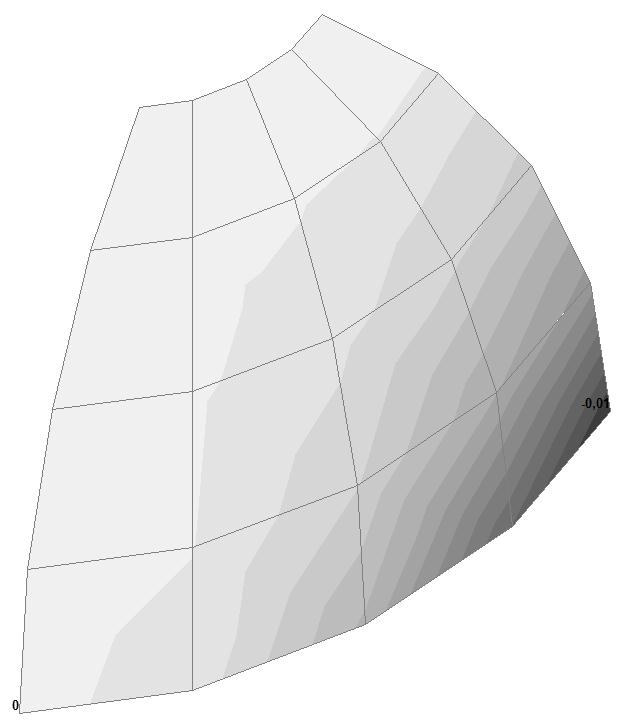
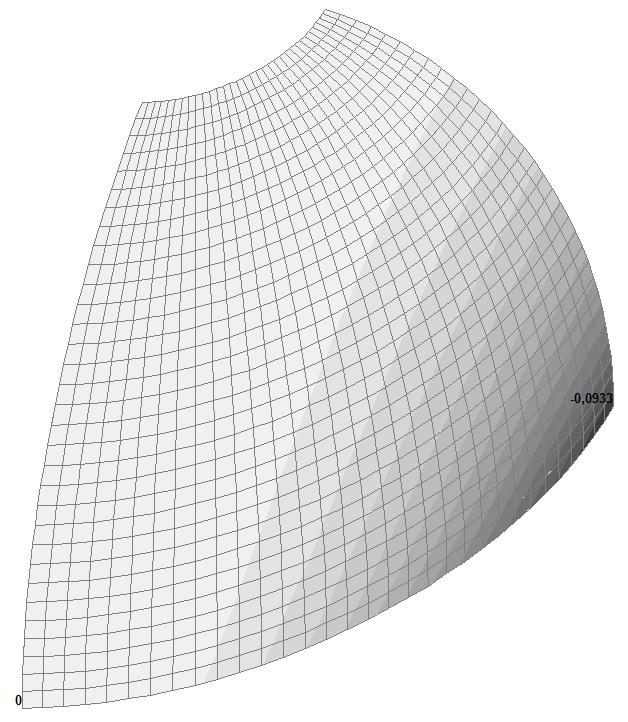
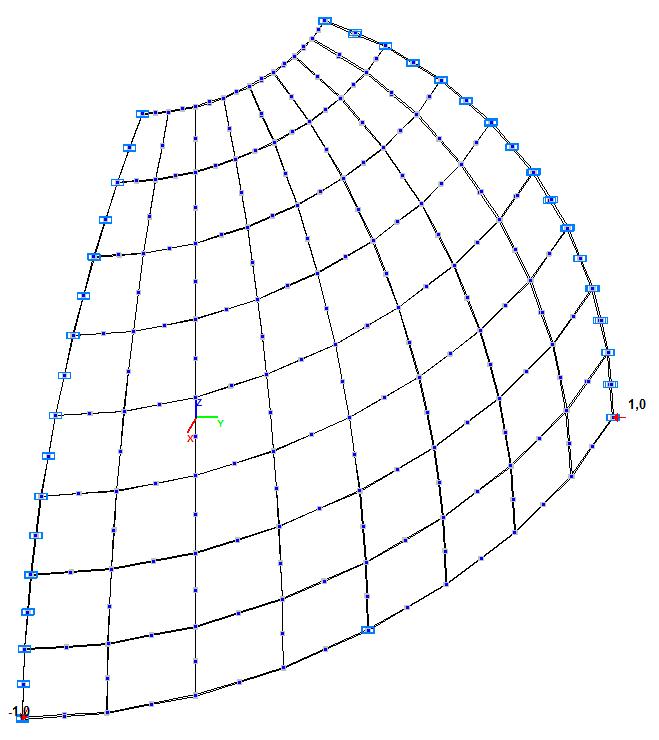
Модель 6. Значения перемещений по направлению пар растягивающих и пар сжимающих сил вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)


Сравнение решений:

Перемещения по направлению пар радиально растягивающих и пар радиально сжимающих сил FX и FY вдоль осей X и Y общей системы координат соответственно wFX  и wFY (м, м)

Модель

Сетка конечных элементов

Теория

SCAD

Отклонение, %

1

(Тип элемента 42)

2x2

+0.0940

–0.0940

+0.0828

–0.0862

11.91

8.30

4x4

+0.0902

–0.0919

4.04

2.23

8x8

+0.0917

–0.0922

2.45

1.91

16x16

+0.0920

–0.0922

2.13

1.91

32x32

+0.0927

–0.0928

1.38

1.28

2

(Тип элемента 44)

2x2

+0.0940

–0.0940

+0.0924

–0.0924

1.70

1.70

4x4

+0.0938

–0.0938

0.21

0.21

8x8

+0.0930

–0.0930

1.06

1.06

16x16

+0.0928

–0.0928

1.28

1.28

32x32

+0.0932

–0.0932

0.85

0.85

3

(Тип элемента 45)

2x2

+0.0940

–0.0940

+0.0506

–0.0510

46.17

45.74

4x4

+0.0389

–0.0395

58.62

57.98

8x8

+0.0484

–0.0489

48.51

47.98

16x16

+0.0834

–0.0835

11.28

11.17

32x32

+0.0927

–0.0927

1.38

1.38

4

(Тип элемента 50)

2x2

+0.0940

–0.0940

+0.0526

–0.0526

44.04

44.04

4x4

+0.0459

–0.0459

51.17

51.17

8x8

+0.0651

–0.0651

30.74

30.74

16x16

+0.0899

–0.0899

4.36

4.36

32x32

+0.0932

–0.0932

0.85

0.85

5

(Тип элемента 36)

2x2

+0.0940

–0.0940

+0.0000

–0.0000

100.00

100.00

4x4

+0.0001

–0.0001

99.89

99.89

8x8

+0.0003

–0.0003

99.68

99.68

16x16

+0.0010

–0.0010

98.94

98.94

32x32

+0.0036

–0.0036

96.17

96.17

64x64

+0.0126

–0.0126

86.60

86.60

128x128

+0.0350

–0.0350

62.77

62.77

256x256

+0.0654

–0.0654

30.43

30.43

512x512

+0.0842

–0.0842

10.43

10.43

6

(Тип элемента 37)

2x2

+0.0940

–0.0940

+0.0014

–0.0014

98.51

98.51

4x4

+0.0100

–0.0100

89.36

89.36

8x8

+0.0589

–0.0590

37.34

37.23

16x16

+0.0900

–0.0900

4.26

4.26

32x32

+0.0933

–0.0933

0.74

0.74

64x64

+0.0936

–0.0936

0.43

0.43

128x128

+0.0937

–0.0937

0.32

0.32