Открытая цилиндрическая оболочка прямоугольная в плане и свободно опертая по криволинейным кромкам под действием равномерно распределенной по всей площади поперечной нагрузки
Цель: Проверка точного воспроизведения значений поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки прямоугольной в плане и свободно опертой по криволинейным кромкам от действия равномерно распределенной по всей площади поперечной нагрузки.
Файлы с исходными данными:
| Расчетная модель с типом элементов 42 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 44 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 45 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 50 для сеток 2x2, 4x4, 8x8 | |
| Расчетная модель с типом элементов 36 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 | |
| Расчетная модель с типом элементов 37 для сеток 2x2, 4x4, 8x8, 16x16, 32x32, 64x64, 128x128 |
Формулировка задачи: Открытая цилиндрическая оболочка прямоугольная в плане и свободно опертая по криволинейным кромкам через торцевые идеальные диафрагмы абсолютно жесткие в их плоскости и абсолютно податливые из их плоскости подвергается воздействию равномерно распределенной по всей площади поперечной нагрузки q. Проверить: точное воспроизведение значений поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq.
Ссылки: R. H. Macneal, R. L. Harder, A proposed standard set of problems to test finite element accuracy, North-Holland, Finite elements in analysis and design, 1, 1985, p. 3-20.
A. C. Scordelis, K. S. Lo, Computer analysis of cylindrical shells, Journal of the American concrete institute, Title No 61-33, May 1964, p. 539-561.
Design of cylindrical concrete shell roofs, New York, Manual No 31 American society of civil engineers, 1952.
Исходные данные:
| E = 4.32·108 кПа | - модуль упругости материала цилиндрической оболочки; |
| ν = 0.00 | - коэффициент Пуассона; |
| L = 50.00 м | - длина образующей цилиндрической оболочки; |
| R = 25.00 м | - радиус срединной поверхности цилиндрической оболочки; |
| 2•θ = 2•40° | - центральный угол дуги направляющей цилиндрической оболочки; |
| h = 0.25 м | - толщина цилиндрической оболочки; |
| q = 90.0 кН/м2 | - значение равномерно распределенной по всей площади цилиндрической оболочки поперечной нагрузки. |
Конечноэлементная модель: Расчетная схема – система общего вида. Рассматривается расчетная схема четверти цилиндрической оболочки по условиям симметрии для шести расчетных моделей:
Модель 1 – 8, 32, 128 трехузловых элемента оболочки типа 42 с регулярной сеткой 2x2, 4x4, 8x8. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных кромок цилиндрической оболочки по направлениям степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 2 – 4, 16, 64 четырехузловых элемента оболочки типа 44 с регулярной сеткой 2x2, 4x4, 8x8. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных кромок цилиндрической оболочки по направлениям степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 9, 25, 81.
Модель 3 - 8, 32, 128 шестиузловых элемента оболочки типа 45 с регулярной сеткой 2x2, 4x4, 8x8. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных кромок цилиндрической оболочки по направлениям степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 4 - 4, 16, 64 восьмиузловых элемента оболочки типа 50 с регулярной сеткой 2x2, 4x4, 8x8. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных кромок цилиндрической оболочки по направлениям степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 25, 81, 289.
Модель 5 - 4, 16, 64, 256, 1024, 4096, 16384 восьмиузловых изопараметрических объемных элемента типа 36 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных ребер цилиндрической оболочки по направлению степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 18, 50, 162, 578, 2178, 8450, 33282.
Модель 6 - 4, 16, 64, 256, 1024, 4096, 16384 двадцатиузловых изопараметрических объемных элемента типа 37 с регулярной сеткой 2x2x1, 4x4x1, 8x8x1, 16x16x1, 32x32x1, 64x64x1, 128x128x1. Обеспечение граничных условий достигается за счет наложения связей на узлы опорных криволинейных ребер цилиндрической оболочки по направлению степеней свободы X, Z и связей по условиям симметрии. Количество узлов в модели – 51, 155, 531, 1955, 7491, 29315, 115971.
Результаты решения в SCAD
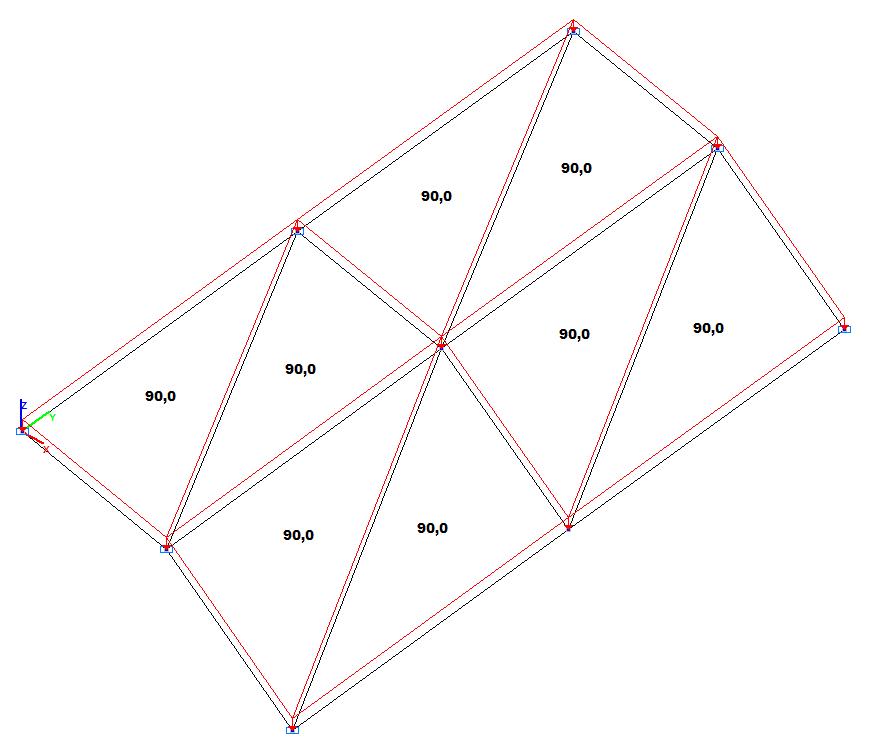
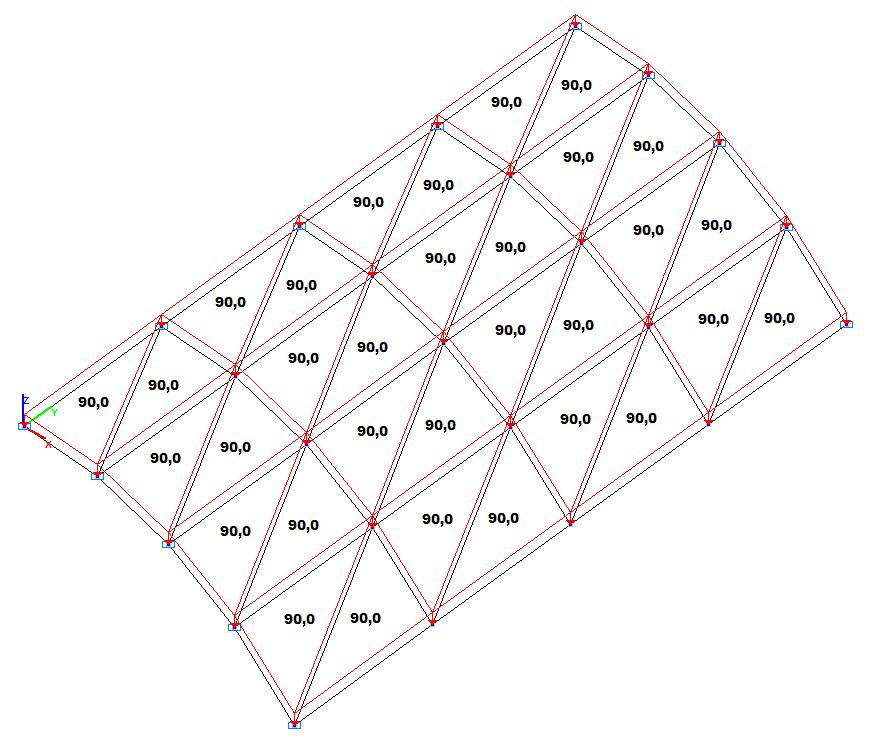

Модель 1. Расчетная схема
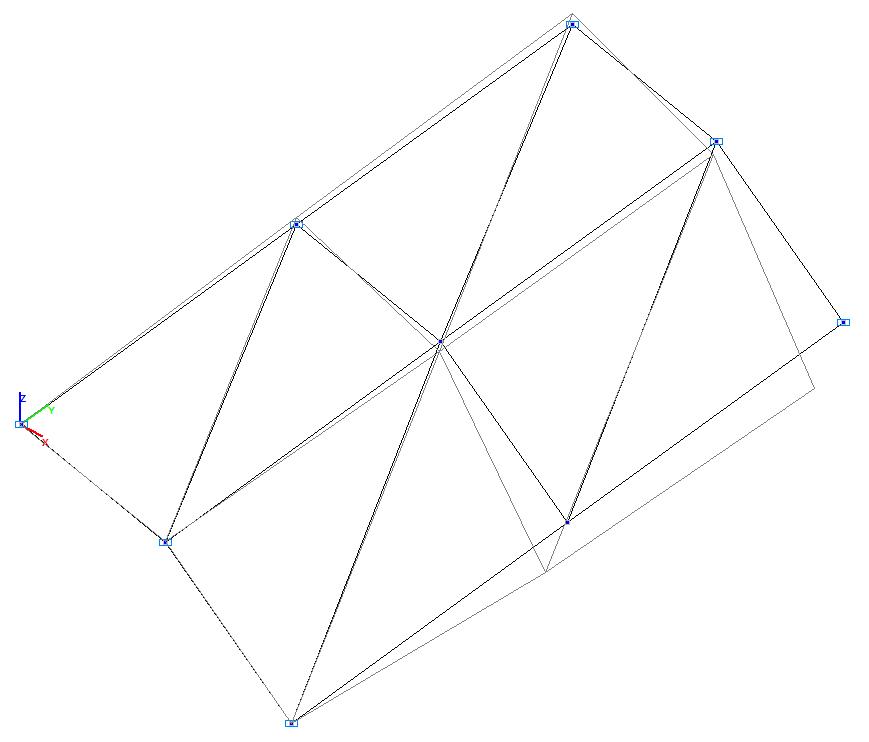
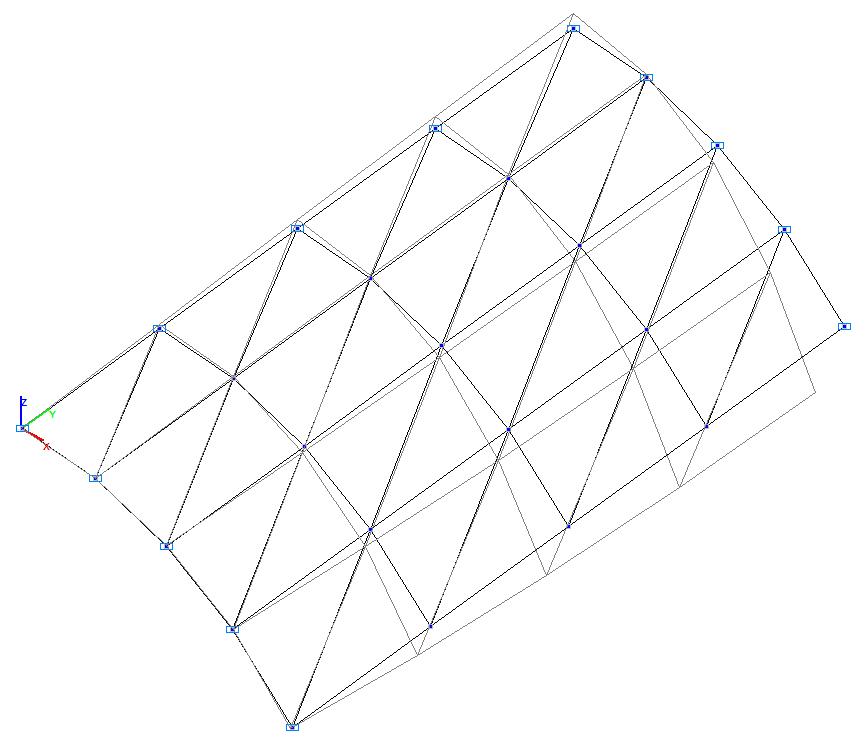
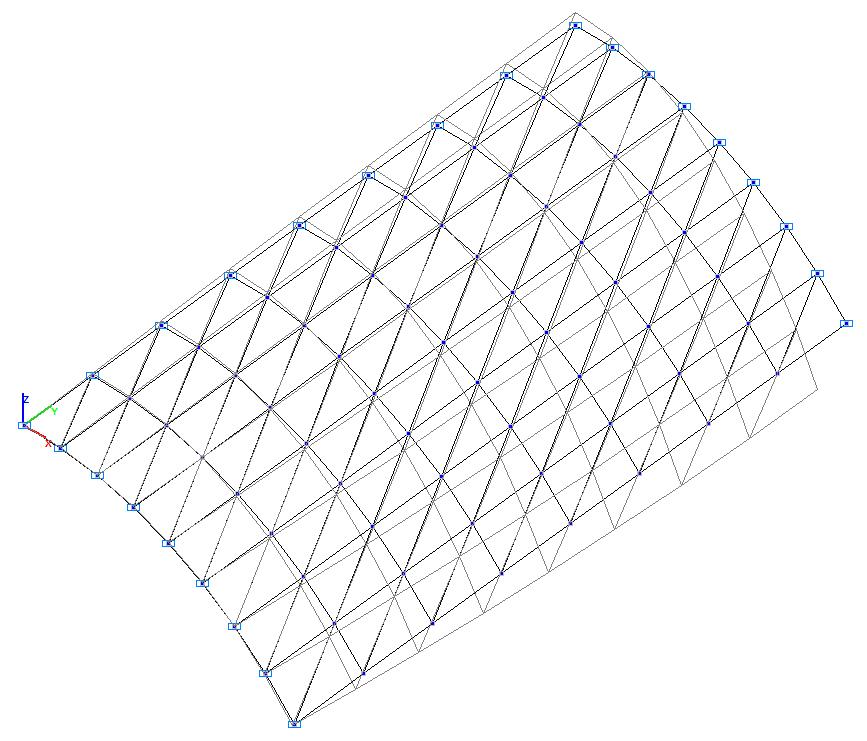
Модель 1. Деформированная схема

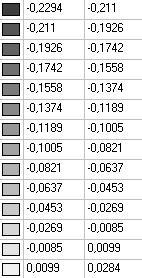

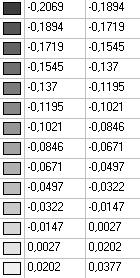

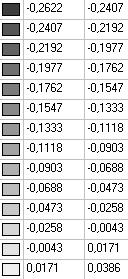
Модель 1. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
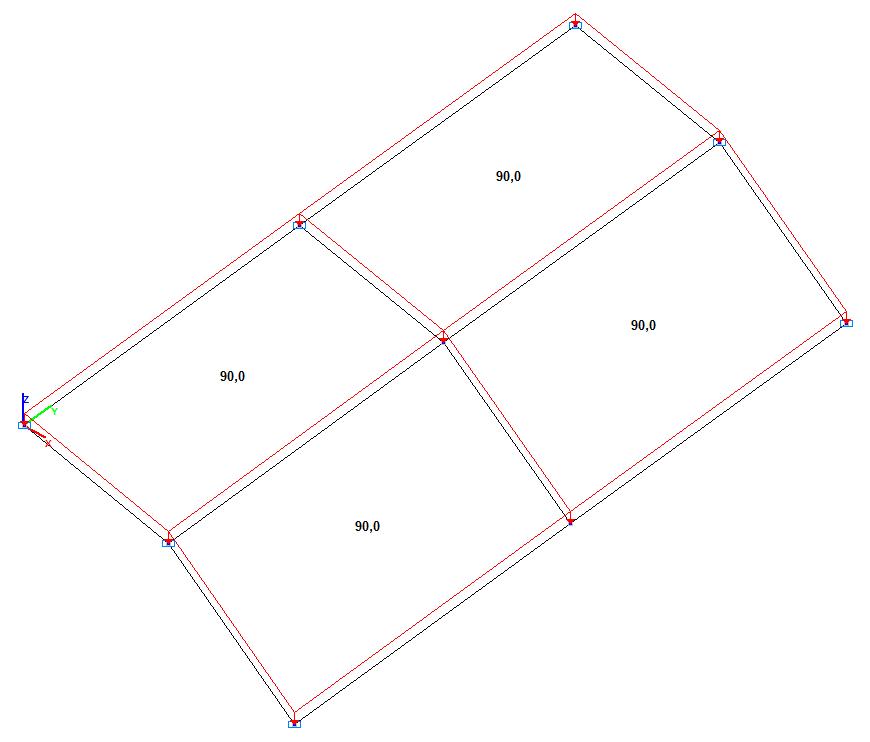
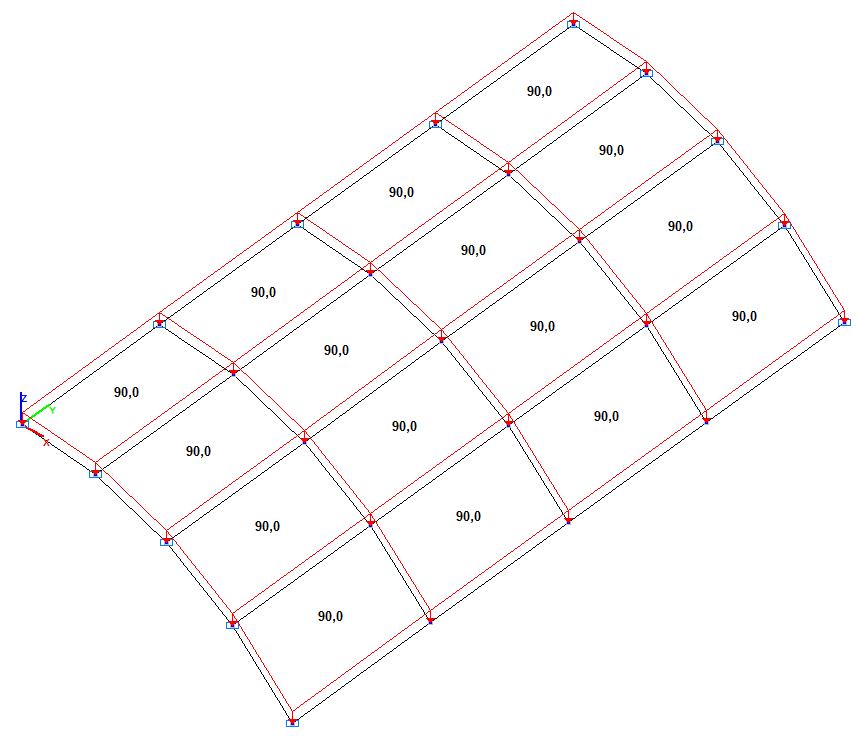

Модель 2. Расчетная схема
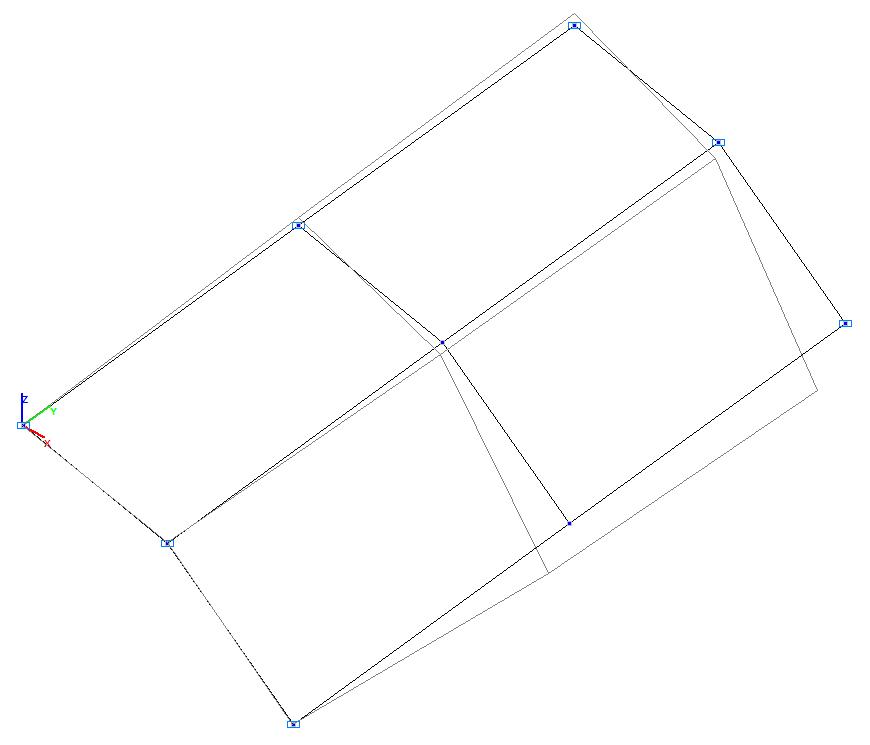
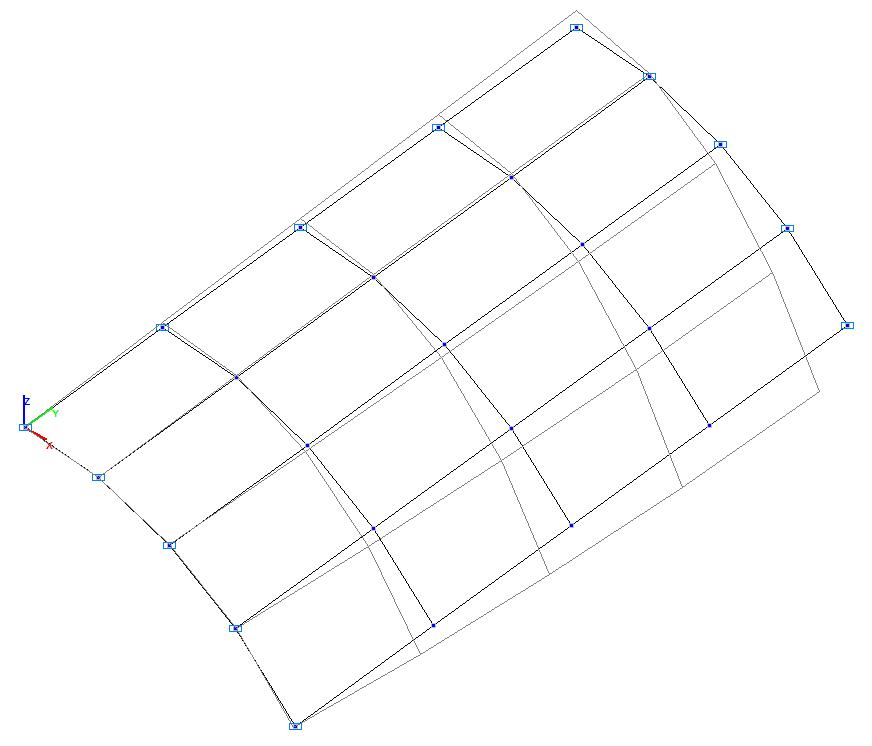
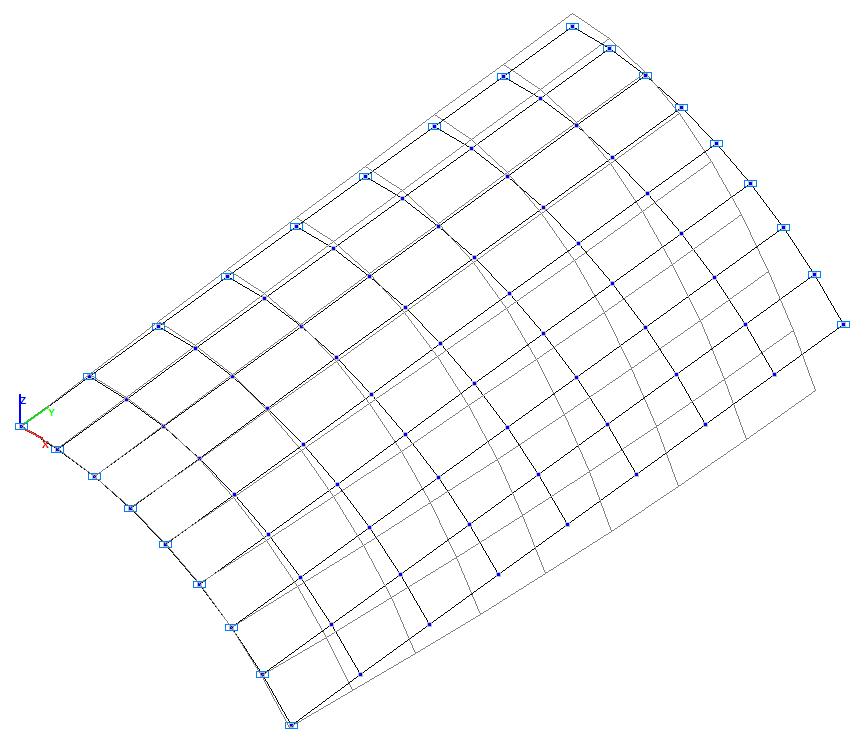
Модель 2. Деформированная схема

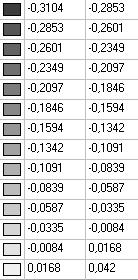

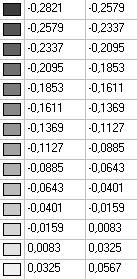


Модель 2. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
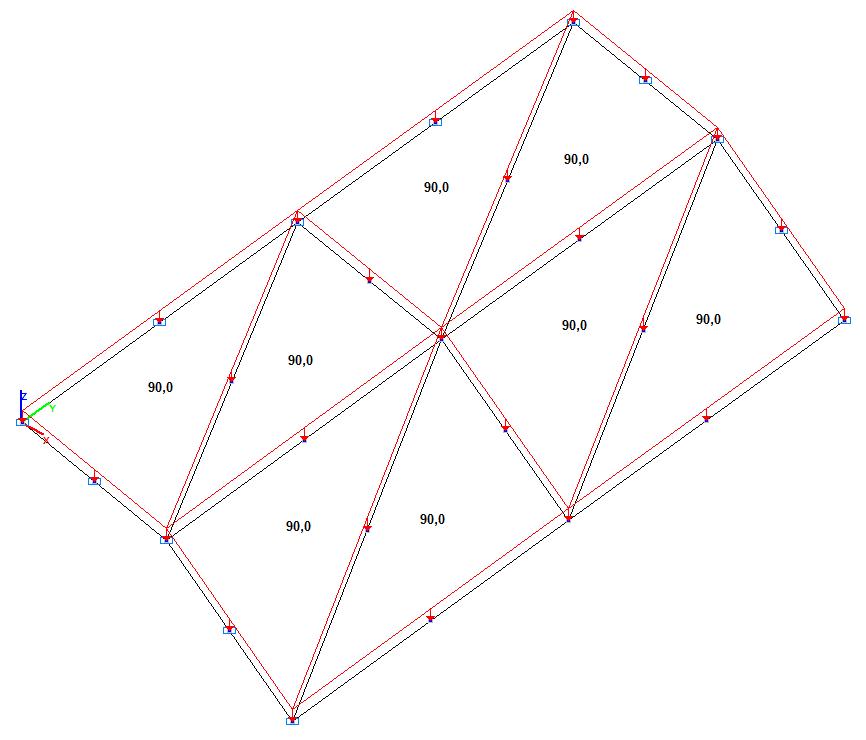
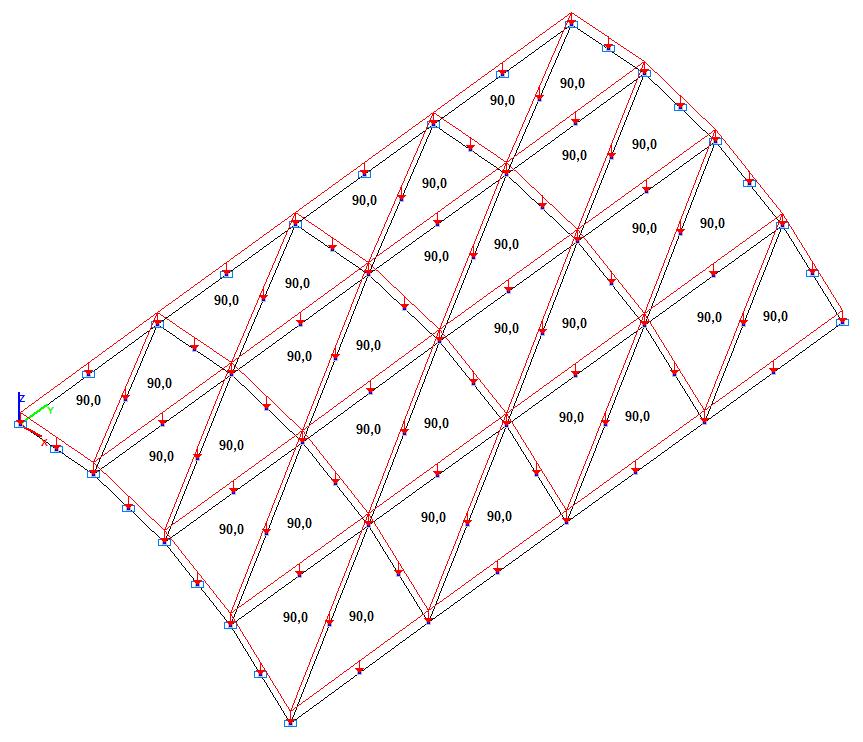

Модель 3. Расчетная схема
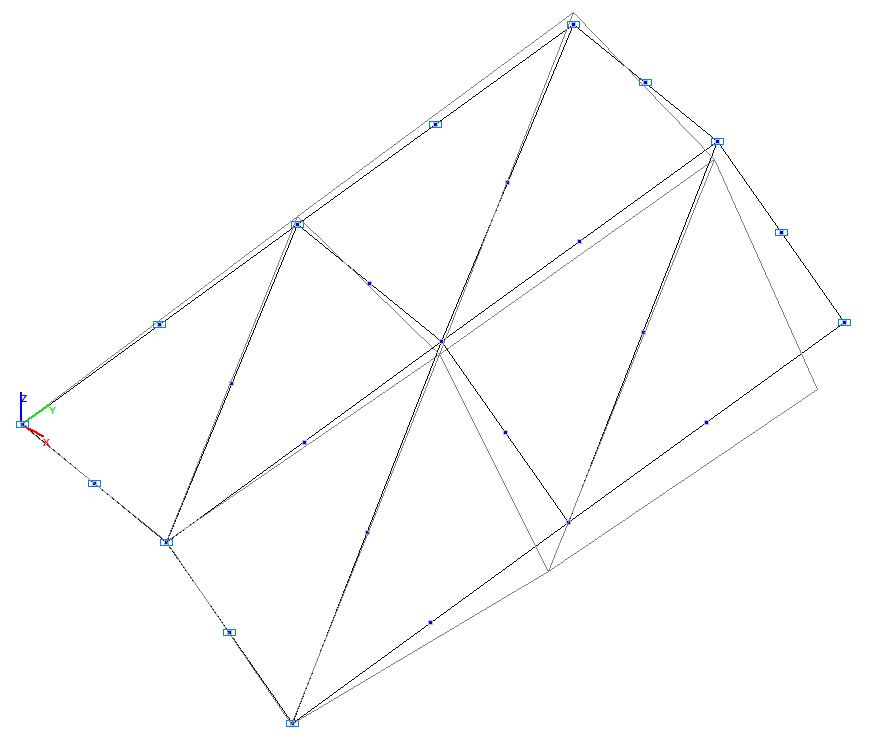
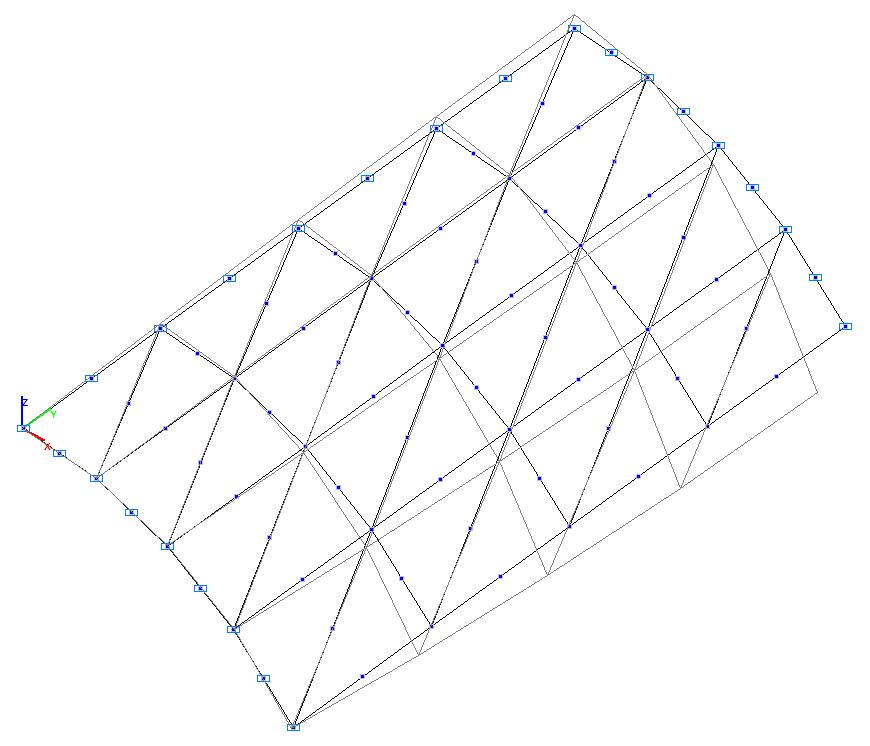
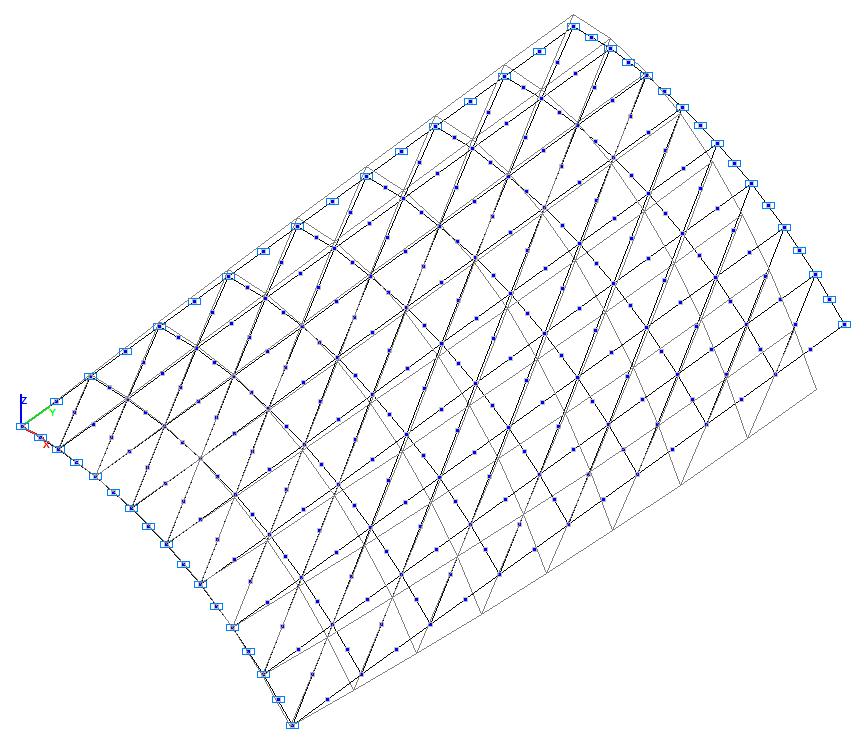
Модель 3. Деформированная схема






Модель 3. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
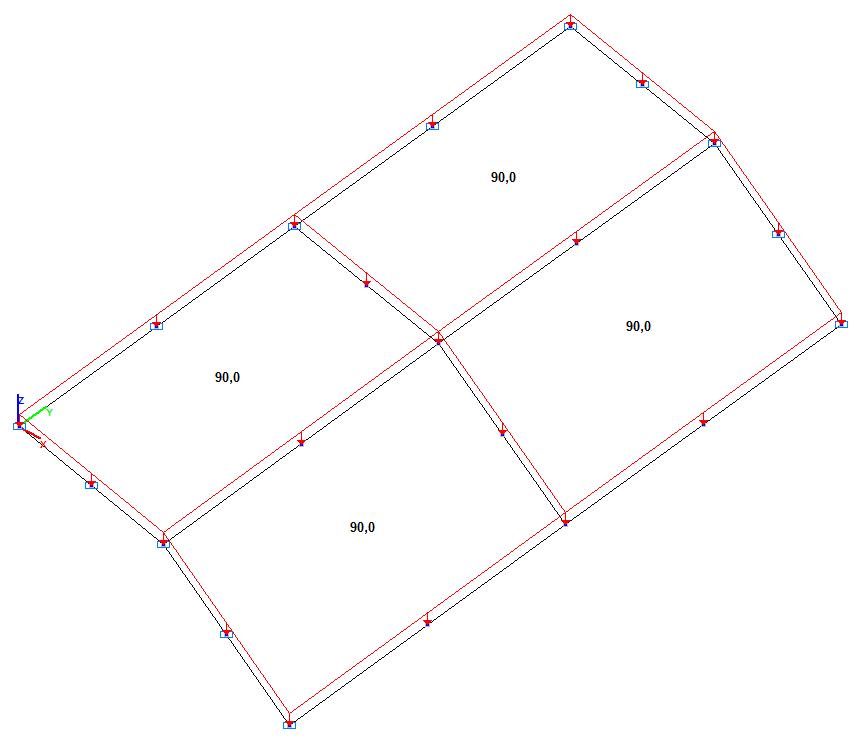
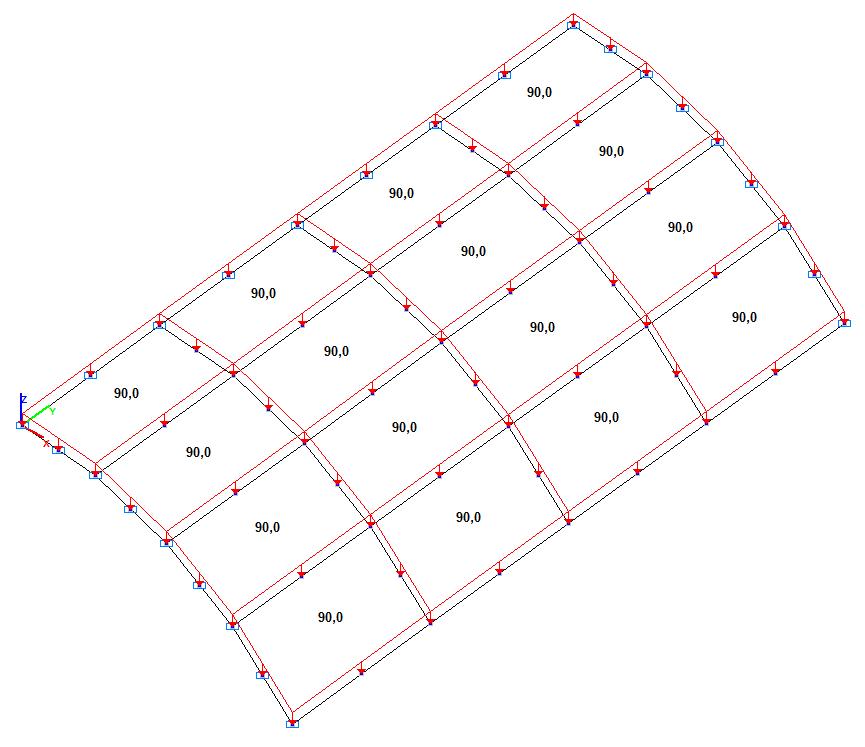

Модель 4. Расчетная схема
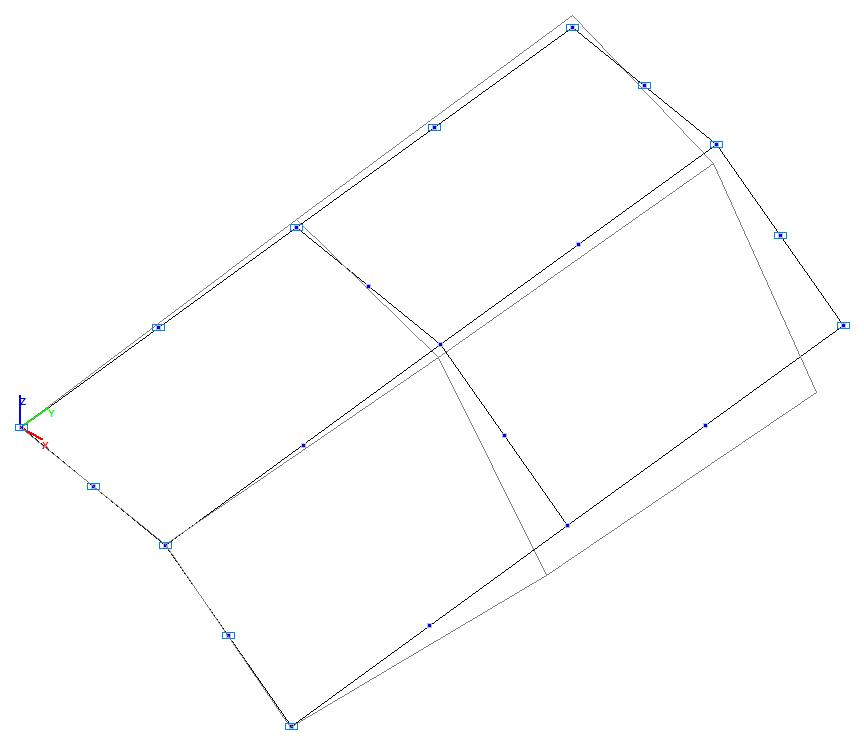
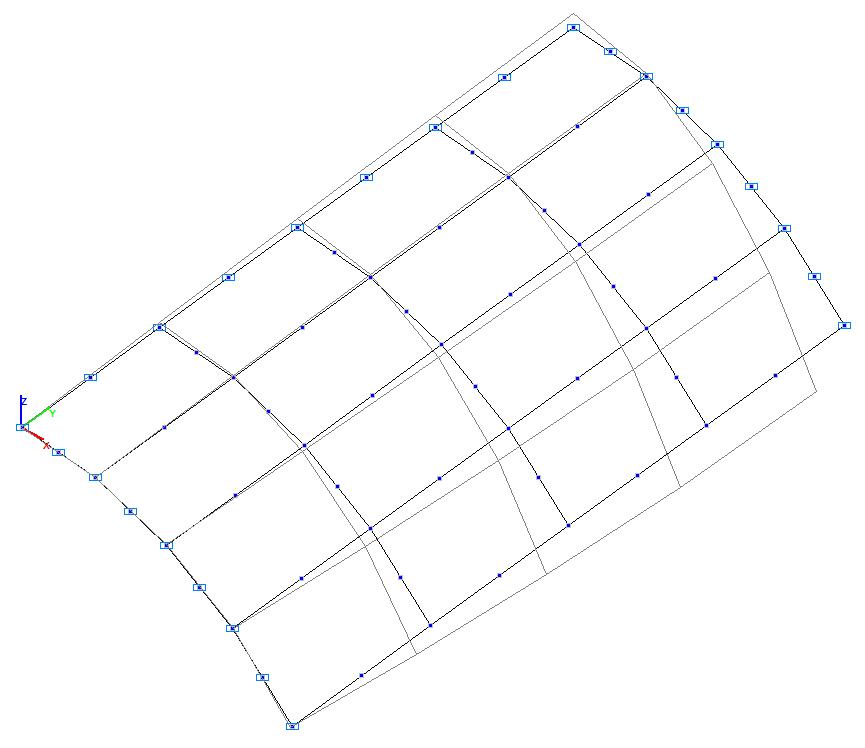
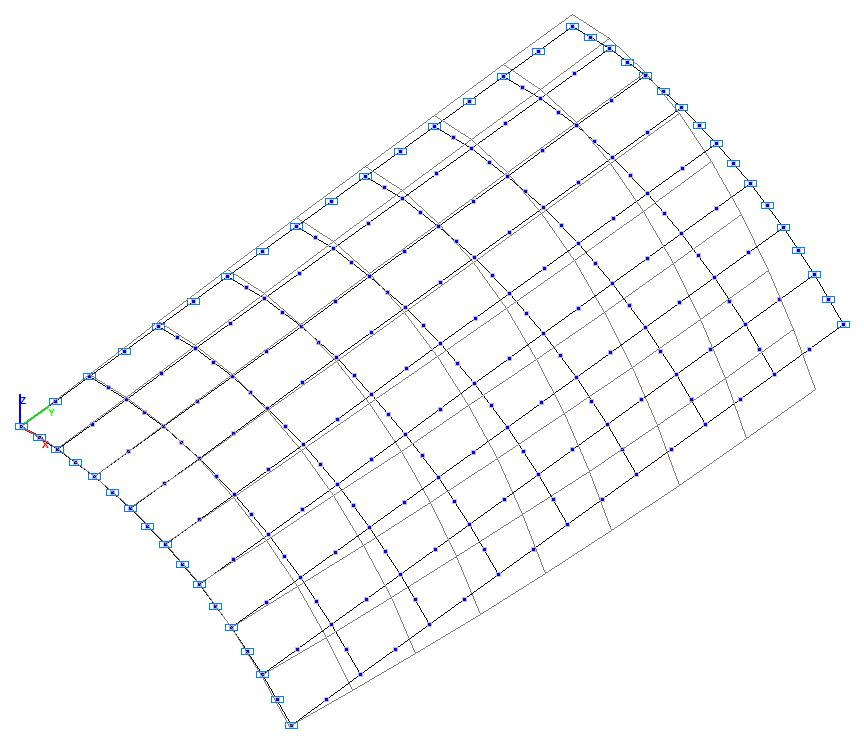
Модель 4. Деформированная схема





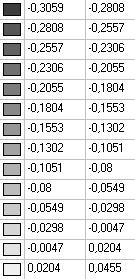
Модель 4. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
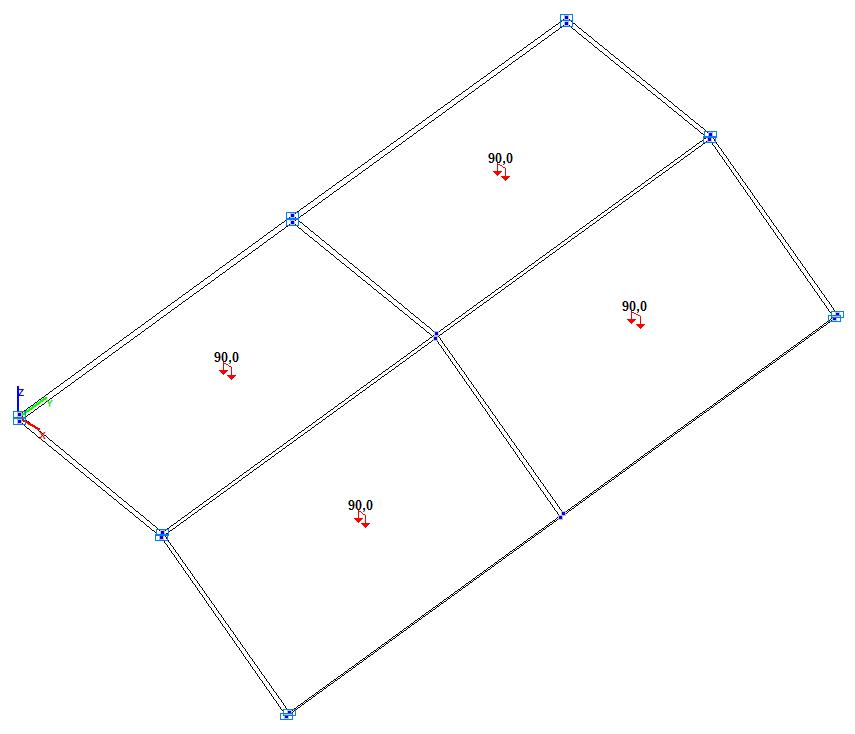
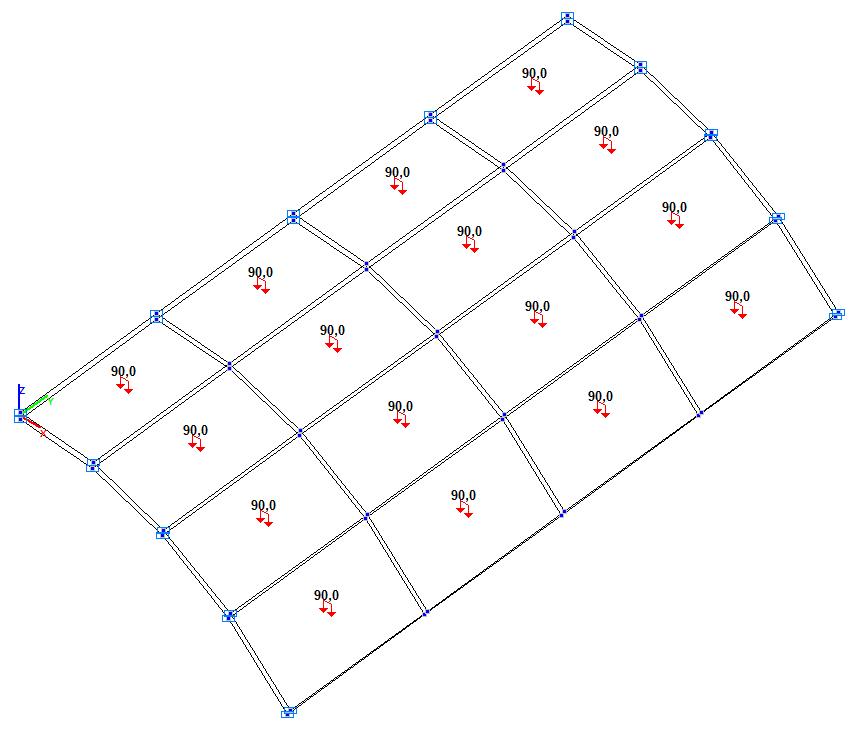
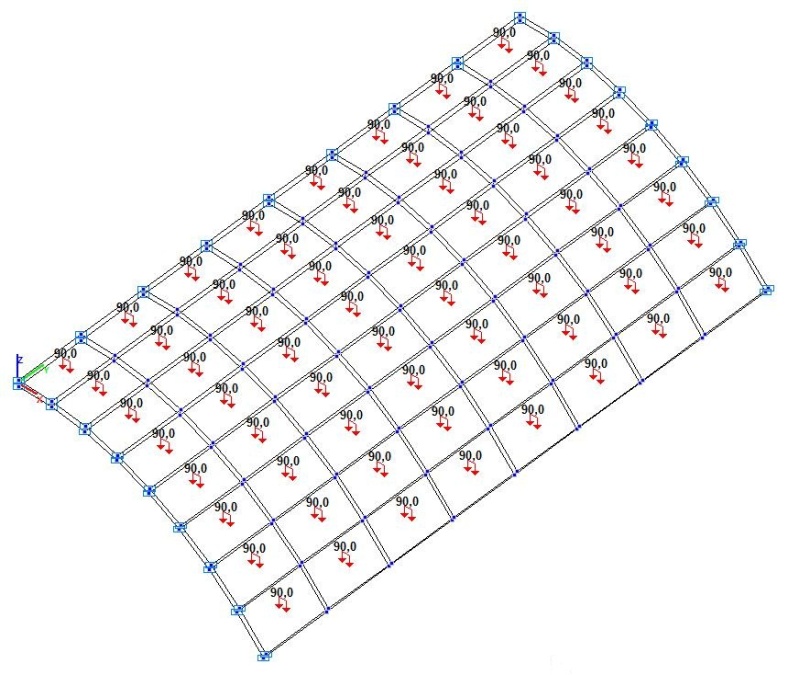




Модель 5. Расчетная схема
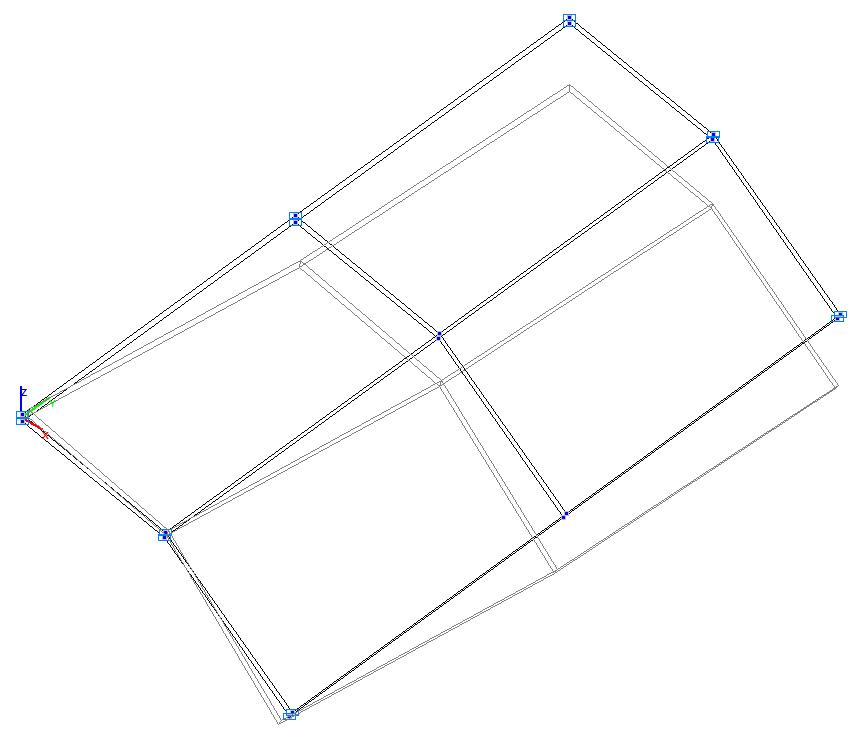
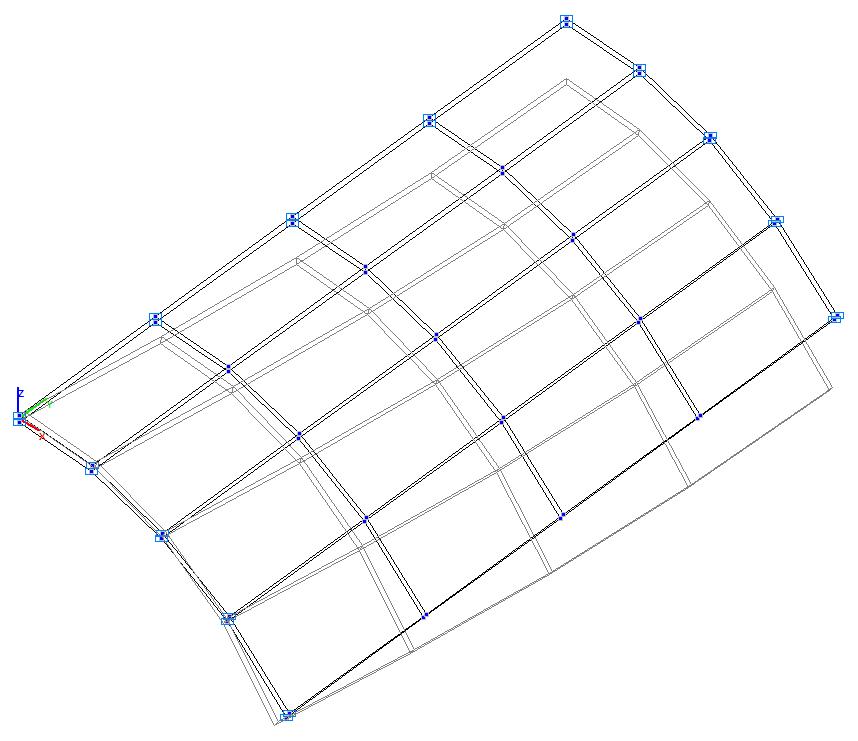
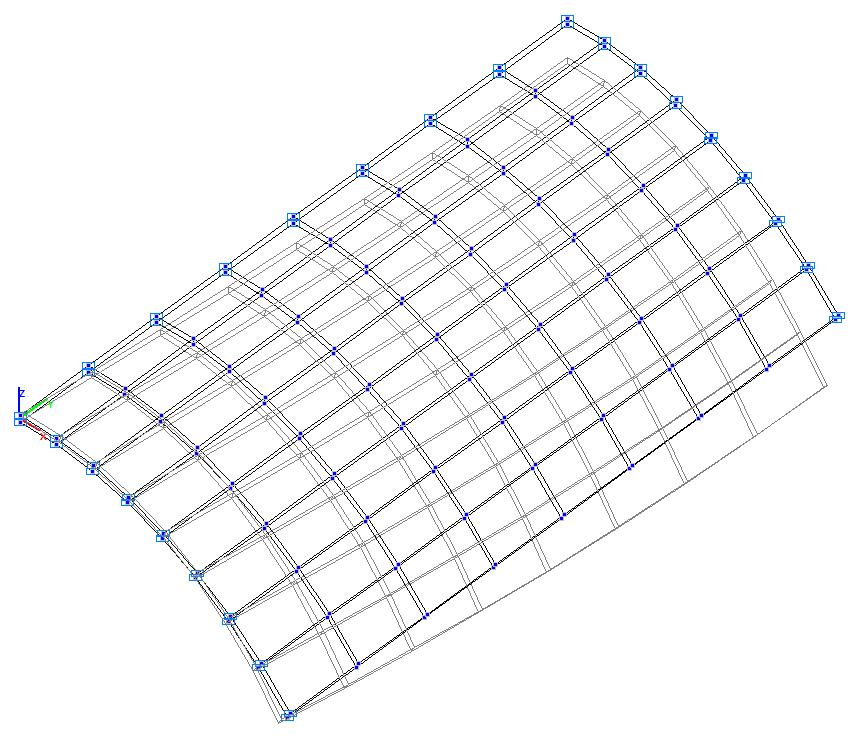




Модель 5. Деформированная схема


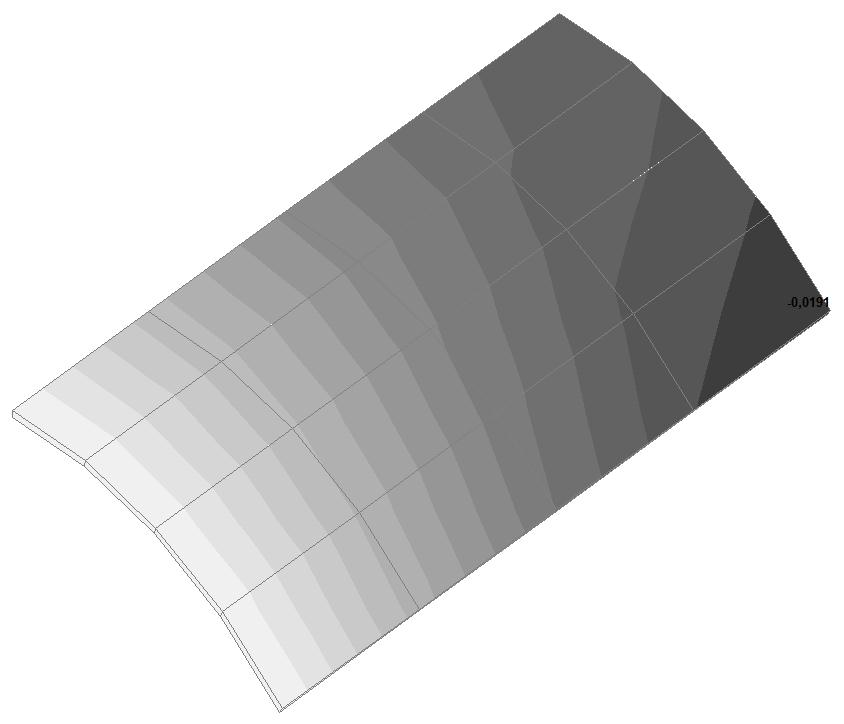
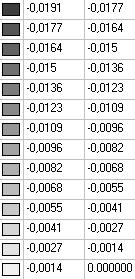

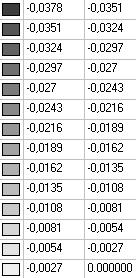







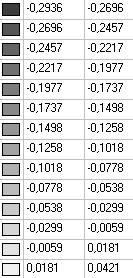
Модель 5. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
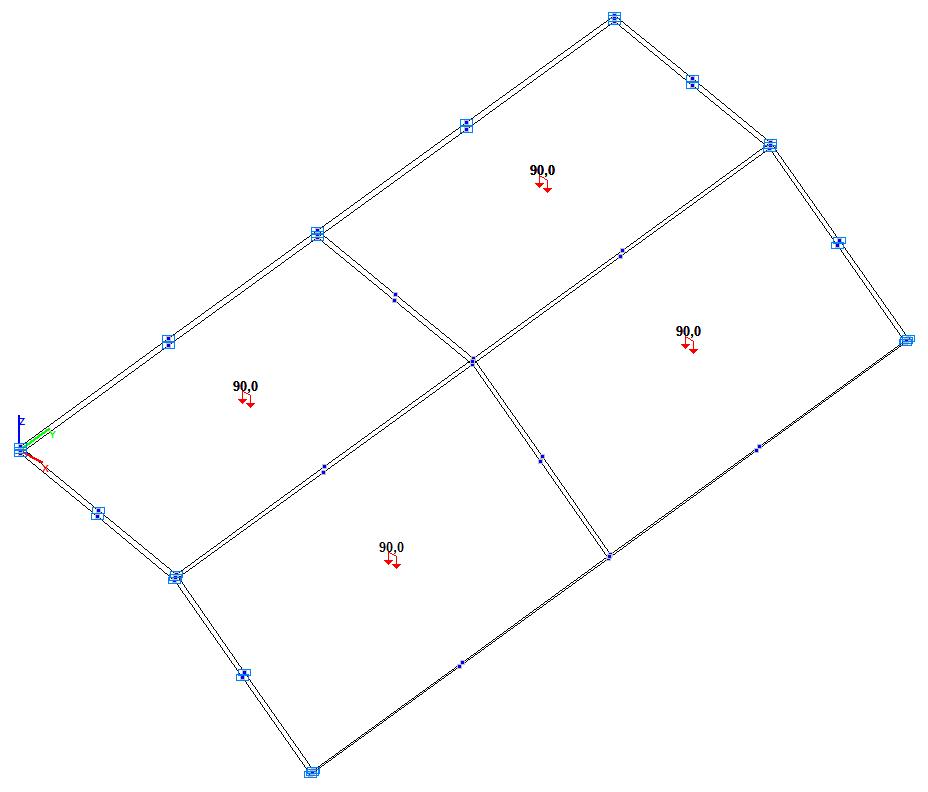
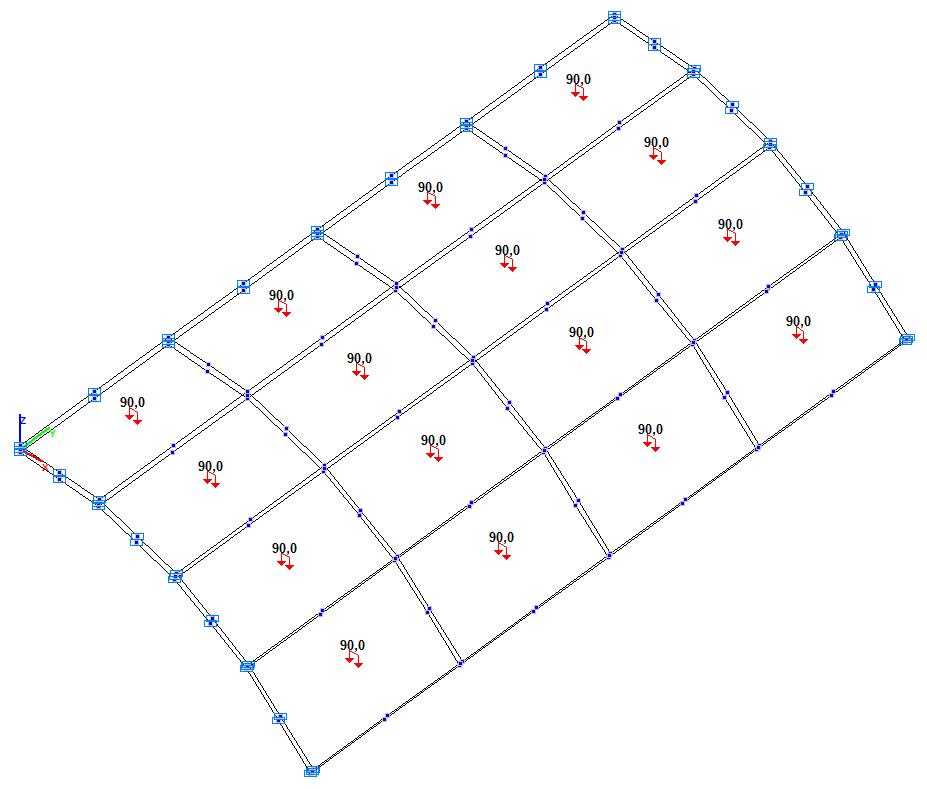
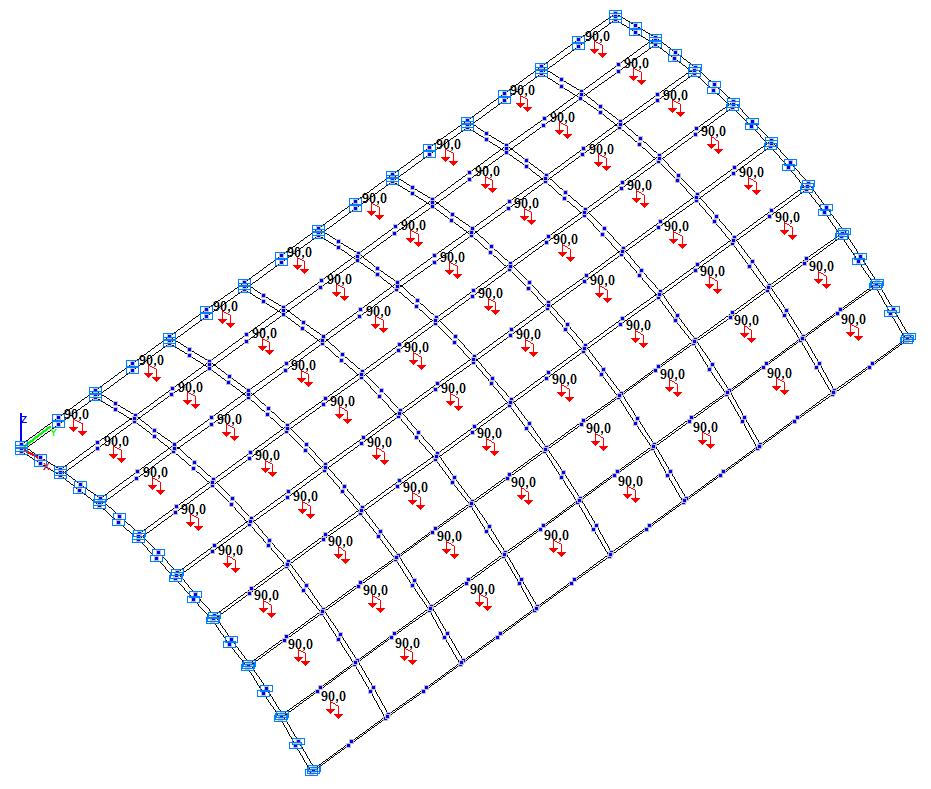




Модель 6. Расчетная схема
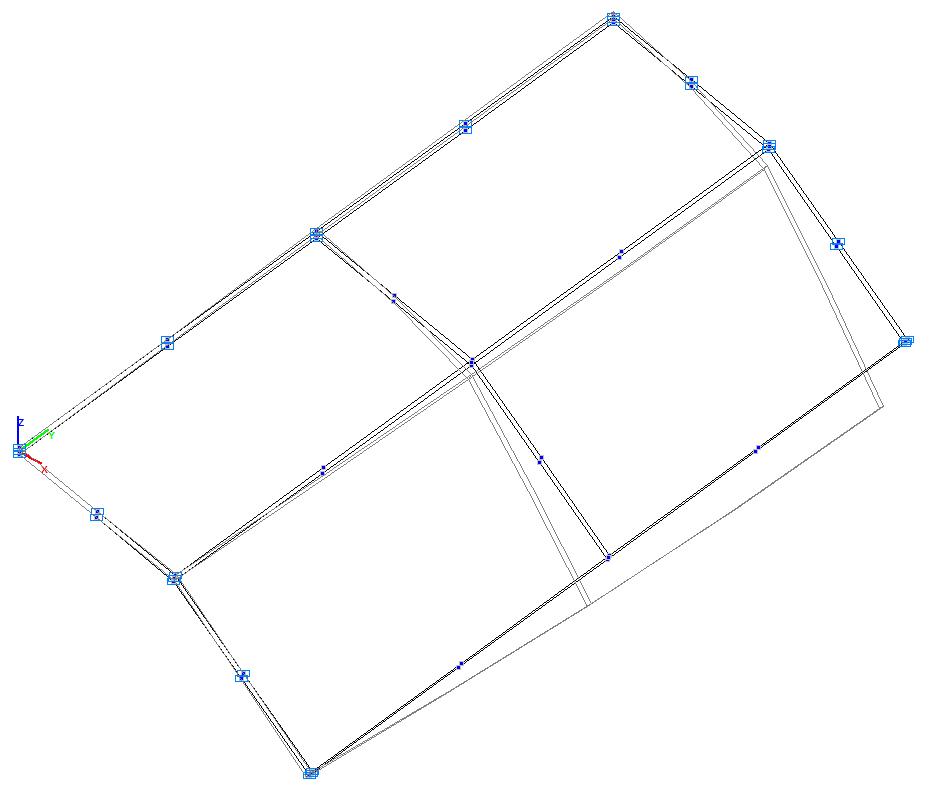
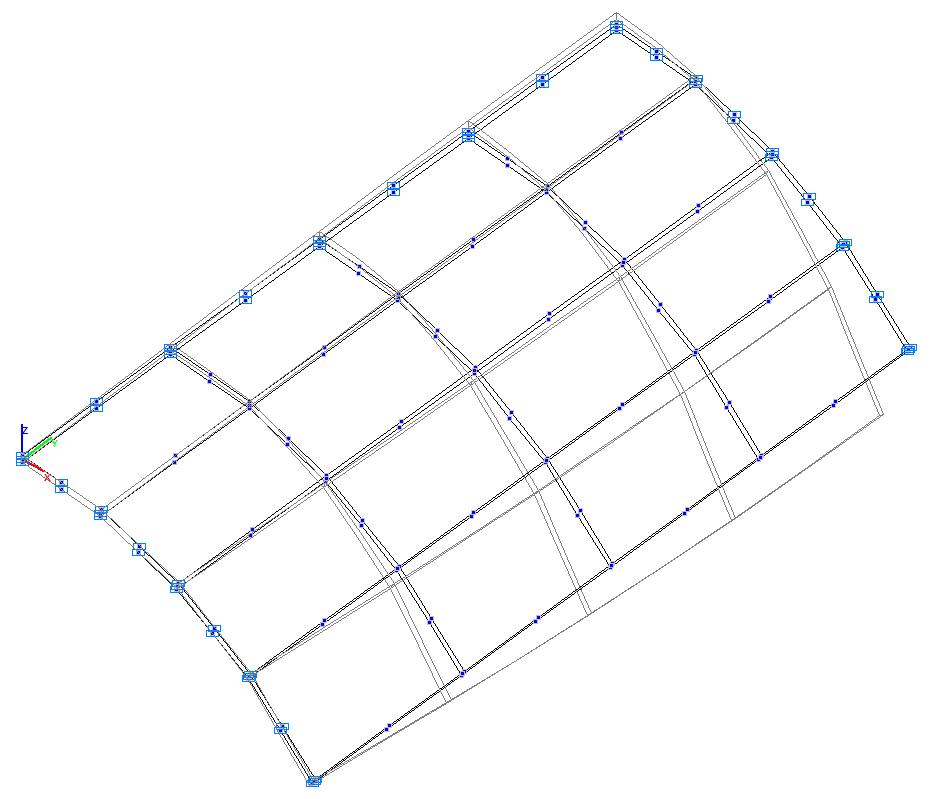
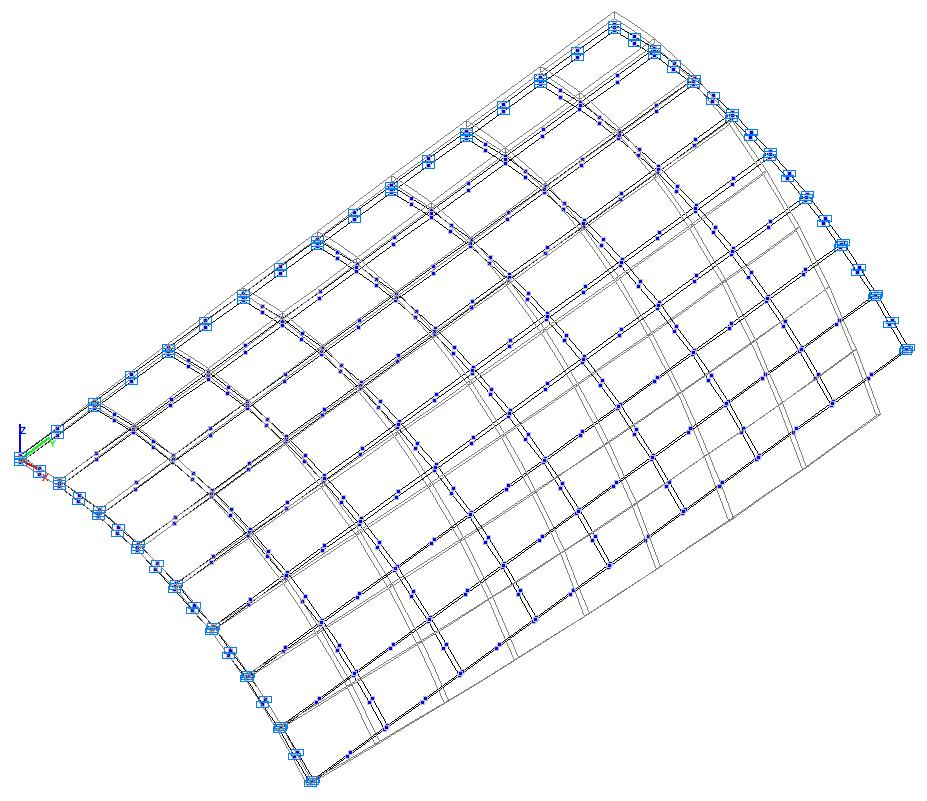




Модель 6. Деформированная схема

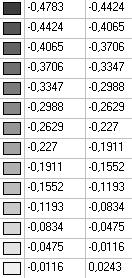

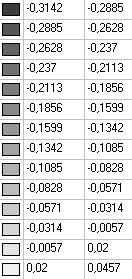

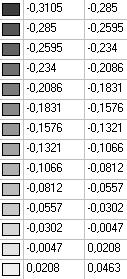








Модель 6. Значения поперечных перемещений в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq (м)
Сравнение решений:
Поперечные перемещения в середине свободных прямолинейных кромок открытой цилиндрической оболочки wq от воздействия равномерно распределенной по всей площади поперечной нагрузки q
|
Модель |
Сетка конечных элементов |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 (Тип элемента 42) |
2x2 |
0.3086 |
0.2294 |
25.66 |
|
4x4 |
0.2069 |
32.95 |
||
|
8x8 |
0.2622 |
15.04 |
||
|
2 (Тип элемента 44) |
2x2 |
0.3086 |
0.3104 |
0.58 |
|
4x4 |
0.2821 |
8.59 |
||
|
8x8 |
0.2941 |
4.70 |
||
|
3 (Тип элемента 45) |
2x2 |
0.3086 |
0.3673 |
19.02 |
|
4x4 |
0.3107 |
0.68 |
||
|
8x8 |
0.3057 |
0.94 |
||
|
4 (Тип элемента 50) |
2x2 |
0.3086 |
0.3693 |
19.67 |
|
4x4 |
0.3114 |
0.91 |
||
|
8x8 |
0.3059 |
0.87 |
||
|
5 (Тип элемента 36) |
2x2 |
0.3086 |
0.0077 |
97.50 |
|
4x4 |
0.0191 |
93.81 |
||
|
8x8 |
0.0378 |
87.75 |
||
|
16x16 |
0.0806 |
73.88 |
||
|
32x32 |
0.1673 |
45.79 |
||
|
64x64 |
0.2532 |
17.95 |
||
|
128x128 |
0.2936 |
4.86 |
||
|
6 (Тип элемента 37) |
2x2 |
0.3086 |
0.4783 |
54.99 |
|
4x4 |
0.3142 |
1.81 |
||
|
8x8 |
0.3105 |
0.62 |
||
|
16x16 |
0.3102 |
0.52 |
||
|
32x32 |
0.3104 |
0.58 |
||
|
64x64 |
0.3103 |
0.55 |
||
|
128x128 |
0.3104 |
0.58 |
