Устойчивость консольной стойки со ступенчатым изменением поперечного сечения, нагруженной продольными сжимающими силами, приложенными к промежуточным и торцевым сечениям
Цель: Определение критических значений продольных сжимающих сил, приложенных к промежуточным и торцевым сечениям консольной стойки со ступенчатым изменением поперечного сечения, соответствующих моменту потери ее устойчивости. Определение свободных длин ступеней стойки.
Использованная версия SCAD: 11.3
Файлы с исходными данными:
|
Расчетная схема из стержневых элементов |
|
|
Расчетная схема из оболочечных элементов |
Формулировка задачи: Консольная стойка со ступенчатым изменением поперечного сечения подвергается воздействию продольных сил Pi, приложенных к промежуточным и торцевым сечениям. Определить критические значения продольных сжимающих сил Pcri, соответствующих моменту потери устойчивости консольной стойки. Определить свободные длины ступеней стойки L0i.
Ссылки: С. П. Тимошенко, Устойчивость стержней, пластин и оболочек, Москва, Наука, 1971, стр. 166.
С. Д. Пономарев, В. Л. Бидерман, К. К. Лихарев, В. М. Макушин, Н. Н. Малинин, В. И. Феодосьев, Основы современных методов расчета на прочность в машиностроении. Расчеты при динамической нагрузке. Устойчивость. Ползучесть. Москва, Машгиз, 1952, стр. 543, 555.
Исходные данные:
| L1 = 10.0 м | - длина первой (верхней) ступени стойки; |
| L2 = 10.0 м | - длина второй (средней) ступени стойки; |
| L3 = 10.0 м | - длина третьей (нижней) ступени стойки; |
| D1 = 2.0 м | - наружный диаметр трубчатого поперечного сечения первой ступени стойки; |
| D2 = 2.0 м | - наружный диаметр трубчатого поперечного сечения второй ступени стойки; |
| D3 = 2.0 м | - наружный диаметр трубчатого поперечного сечения третьей ступени стойки; |
| t1 = 0.01 м | - толщина трубчатого поперечного сечения первой ступени стойки; |
| t2 = 0.02 м | - толщина трубчатого поперечного сечения второй ступени стойки; |
| t3 = 0.04 м | - толщина трубчатого поперечного сечения третьей ступени стойки; |
| E = 2.06·108 кН/м2 | - модуль упругости материала стойки; |
| ν = 0.3 | - коэффициент Пуассона; |
| P1 = 1.0·104 кН/м2 | - начальное значение сжимающей продольной силы, приложенной к верхнему торцу первой ступени стойки; |
| P2 = 1.0·104 кН/м2 | - начальное значение сжимающей продольной силы, приложенной к верхнему торцу второй ступени стойки; |
| P3 = 2.0·104 кН/м2 | - начальное значение сжимающей продольной силы, приложенной к верхнему торцу третьей ступени стойки; |
Конечноэлементная модель: Рассматриваются две расчетные модели:
Стержневая модель, расчетная схема – плоская рама, 30 стержневых элементов плоской рамы типа 2. Сетка конечных элементов разбита по длине продольной оси стойки (вдоль осей X1 местных систем координат) с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на защемленный узел стойки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. На узлах верхних торцов ступеней стойки задаются сосредоточенные силы с начальными значениями P1, P2, P3. Количество узлов – 31.
Оболочечная модель, расчетная схема – система общего вида, 60400 четырехузловых элементов пологой оболочки с учетом сдвига типа 150. Сетка конечных элементов стойки разбита в кольцевом направлении (вдоль осей X1 местных систем координат) с шагом 3.6°, по длине продольной оси (вдоль осей Y1 местных систем координат) с шагом 0.0625 м. В целях обеспечения условий против местной потери устойчивости оболочки стойки внутри нее установлены горизонтальные кольцевые ребра жесткости шириной 0.25 м и с шагом по высоте 1.00 м. Сетка конечных элементов ребер разбита в радиальном направлении (вдоль осей Y1 местных систем координат) с шагом 0.0625 м. Обеспечение граничных условий достигается за счет наложения связей на узлы защемленного торца по направлениям степеней свободы X, Y, Z, UX, UY, UZ. На узлах верхних торцов ступеней стойки задаются равномерно распределенные по линии нагрузки с начальными значениями P1/(π·D1), P2/(π·D2), P3/(π·D3). Количество узлов – 60500.
Результаты решения в SCAD



Расчетная схема стержневой модели

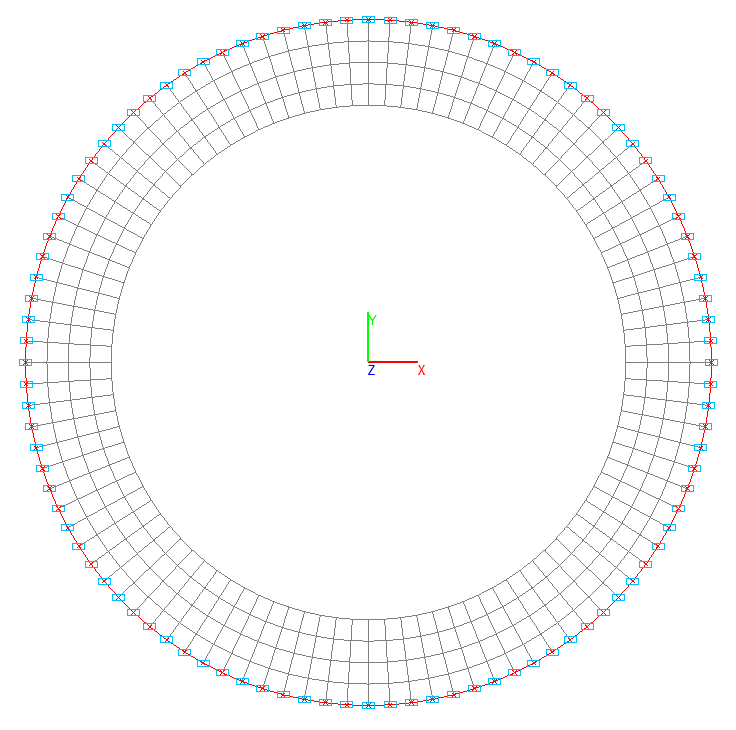
Расчетная схема оболочечной модели
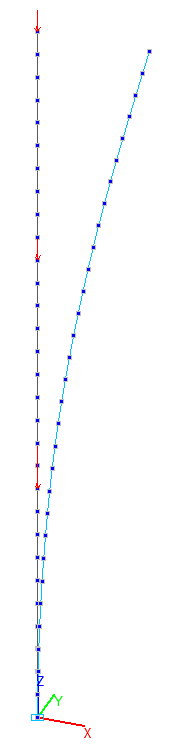
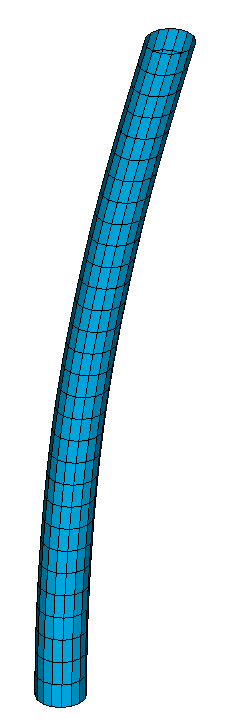
1-я форма потери устойчивости для стержневой модели
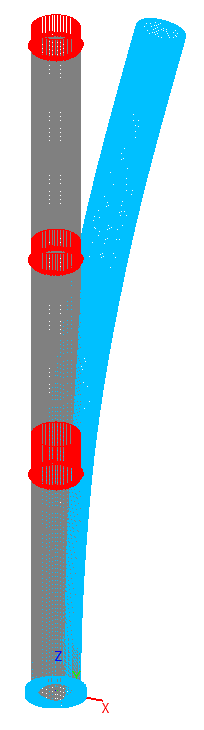

1-я форма потери устойчивости для оболочечной модели
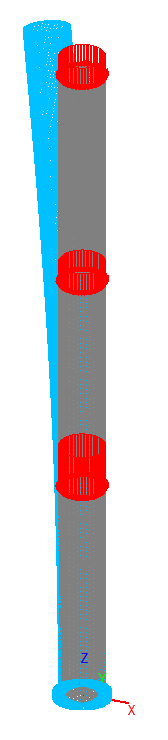

2-я форма потери устойчивости для оболочечной модели
Сравнение решений:
|
Параметр |
Теория |
SCAD |
|||
|---|---|---|---|---|---|
|
Стержневая модель |
Отклонение, % |
Оболочечная модель |
Отклонение, % |
||
|
Критическое значение сосредоточенной продольной силы на верхнем торце первой ступени Pcr1, кН |
32978 |
3.297920∙ ·10000 = = 32979 |
0.00 |
3.394470∙ ·10000 = = 33945 |
2.93 |
|
Критическое значение сосредоточенной продольной силы на верхнем торце второй ступени Pcr2, кН |
32978 |
3.297920∙ ·10000 = = 32979 |
0.00 |
3.394470∙ ·10000 = = 33945 |
2.93 |
|
Критическое значение сосредоточенной продольной силы на верхнем торце третьей ступени Pcr3, кН |
65957 |
3.297920∙ ·20000 = = 65958 |
0.00 |
3.394470∙ ·20000 = = 67890 |
2.93 |
|
Свободная длина первой ступени стойки L01, м |
43.680 |
43.681 |
0.00 |
— |
— |
|
Свободная длина второй ступени стойки L02, м |
43.353 |
43.353 |
0.00 |
— |
— |
|
Свободная длина третьей ступени стойки L03, м |
42.704 |
42.705 |
0.00 |
— |
— |
Замечания: При аналитическом решении критические значения продольных сжимающих сил Pcri, соответствующих моменту потери устойчивости консольной стойки и свободные длины ступеней стойки L0i определяются по следующим формулам:
\[ P_{cr1} =k\cdot P_{1} ; \quad P_{cr2} =k\cdot P_{2} ; \quad P_{cr3} =k\cdot P_{3} ; \] \[ L_{01} =\pi \cdot \sqrt {\frac{E\cdot I_{1} }{k\cdot P_{1} }} ; \quad L_{02} =\pi \cdot \sqrt {\frac{E\cdot I_{2} }{k\cdot \left( {P_{1} +P_{2} } \right)}} ; \quad L_{03} =\pi \cdot \sqrt {\frac{E\cdot I_{3} }{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}} , \quad где \]
k – коэффициент запаса устойчивости системы определяется из условия равенства нулю определителя системы разрешающих уравнений:
\[ \left| {{\begin{array}{*{20}c} {\sin \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{1} +L_{2} +L_{3} } \right)} \right]} & {\cos \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{1} +L_{2} +L_{3} } \right)} \right]} & 0 \\ 0 & 0 & 0 \\ {\frac{P_{1} }{P_{1} +P_{2} }\cdot \sin \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & {\frac{P_{1} }{P_{1} +P_{2} }\cdot \cos \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & {-\sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} \\ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \cos \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & {-\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \sin \left[ {\sqrt {\frac{k\cdot P_{1} }{E\cdot I_{1} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & {-\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} \\ 0 & 0 & {\frac{P_{1} +P_{2} }{P_{1} +P_{2} +P_{3} }\cdot \sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot L_{3} } \right]} \\ 0 & 0 & {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot L_{3} } \right]} \\ \end{array} }} \right. \] \[ \left. {{\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} } & 0 \\ {-\cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & 0 & 0 \\ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \left( {L_{2} +L_{3} } \right)} \right]} & 0 & 0 \\ {\frac{P_{1} +P_{2} }{P_{1} +P_{2} +P_{3} }\cdot \cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot L_{3} } \right]} & {-\sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot L_{3} } \right]} & {-\cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot L_{3} } \right]} \\ {-\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot \sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} } \right)}{E\cdot I_{2} }} \cdot L_{3} } \right]} & {-\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot \cos \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot L_{3} } \right]} & {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot \sin \left[ {\sqrt {\frac{k\cdot \left( {P_{1} +P_{2} +P_{3} } \right)}{E\cdot I_{3} }} \cdot L_{3} } \right]} \\ \end{array} }} \right|=0 \]
