Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой
Цель: Нагружение защемленной по концам балки в одной плоскости без учета деформаций поперечного сдвига. Проверяются значения максимальных поперечного перемещения и изгибающих моментов.
Файл с исходными данными: 4_4.spr
Формулировка задачи: Защемленная по концам балка нагружается равномерно распределенной нагрузкой q. Определить максимальные поперечное перемещение w и изгибающие моменты М.
Ссылки: Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988.
Исходные данные:
| E = 2.0·1011 Па | - модуль упругости, |
| μ = 0.3 | - коэффициент Пуассона, |
| l = 3 м | - длина балки; |
| F = 14.2·10-4 м2 | - площадь поперечного сечения; |
| I = 2.44·10-6 м4 | - момент инерции; |
| q = 10 кН/м | - значение нагрузки. |
Конечноэлементная модель: Расчетная схема плоская рама, 10 стержневых элементов типа 2, 11 узлов.
Результаты решения в SCAD

Эпюра изгибающего момента М (кН*м)
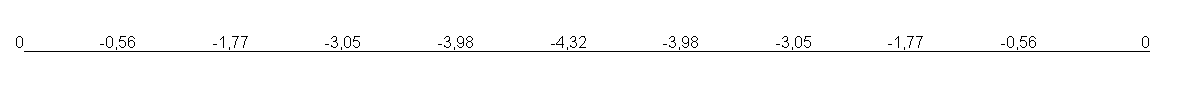
Значение поперечных перемещений w (мм).
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
Поперечное перемещение в середине пролета балки, мм |
-4.32 |
-4.32 |
0.00 |
|
Изгибающий момент в середине пролета балки, кН·м |
3.75 |
3.75 |
0.00 |
|
Изгибающий момент на опоре балки, кН·м |
-7.5 |
-7.5 |
0.00 |
Замечания: При аналитическом решении прогиб в центре балки может быть вычислен по следующей формуле ( «Справочник по сопротивлению материалов» стр. 352):
\[ w=-\frac{q\cdot l^{4}}{384\cdot E\cdot I}; \]
Изгибающие моменты в заделке вычисляются по следующей формуле:
\[ M=-\frac{q\cdot l^{2}}{12}; \]
Изгибающий момент в центре балки:
\[ M=\frac{q\cdot l^{2}}{24}. \]
