Устойчивость консольного бруса квадратного поперечного сечения под действием сосредоточенной продольной сжимающей силы, центрально приложенной на свободном торце (центральное сжатие)

Цель: Определение первых двух критических значений сосредоточенной продольной сжимающей силы, действующей центрально на свободном торце консольного бруса квадратного поперечного сечения, соответствующих моментам потери его устойчивости.

Файлы с исходными данными:

Имя файла	Описание файла расчета
Stability_Bar_1_Bar.SPR	Стержневая расчетная модель
Stability_Bar_1_Shell.SPR	Оболочечная расчетная модель
Stability_Bar_1_Solid.SPR	Объемная расчетная модель

Формулировка задачи: Консольный брус квадратного поперечного сечения подвергается воздействию сосредоточенной продольной сжимающей силы P, центрально действующей на его свободном торце. Определить первые два критические значения сосредоточенной продольной сжимающей силы P_cr1 и P_cr2, соответствующие моментам потери устойчивости консольного бруса.  

Ссылки: А. С. Вольмир, Устойчивость деформируемых систем, Москва, Наука, 1967, стр.23, 193;

Исходные данные:

L = 10.0 м	- длина консольного бруса;
h = b = 1.0 м	- сторона квадратного поперечного сечения консольного бруса;
E = 3.0·107 кН/м2	- модуль упругости материала консольного бруса;
ν = 0.2	- коэффициент Пуассона;
P = 105 кН	- начальное значение сосредоточенной продольной сжимающей силы, центрально действующей на свободном торце бруса.

 

Конечноэлементная модель: Расчетная  схема – система общего вида. Рассматриваются три расчетные модели:

 

Стержневая модель (С), 10 элементов типа 5, сетка конечных элементов разбита по длине продольной оси полосы с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на узел защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной продольной сжимающей силы P задается в узле свободного торца бруса. Количество узлов в расчетной схеме – 11;

Оболочечная модель теории Рейсснера-Миндлина (П), 2560 восьмиузловых элементов типа 150, сетка конечных элементов разбита по длине продольной оси и высоте бруса с шагом 0.0625 м. Обеспечение граничных условий достигается за счет наложения связей на узлы защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной продольной сжимающей силы P задается в узле продольной оси бруса, расположенном на свободном торце. Количество узлов в расчетной схеме – 8033.

Объемная модель (О), 5120 двадцатиузловых элементов типа 37, сетка конечных элементов разбита по длине продольной оси, ширине и высоте бруса с шагом 0.125 м. Обеспечение граничных условий достигается за счет наложения связей на узлы защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной продольной сжимающей силы P задается в виде равномерно распределенной нагрузки по наружным граням элементов торца бруса p = P/(h·b). Количество узлов в расчетной схеме – 24705.

 

Результаты решения в SCAD

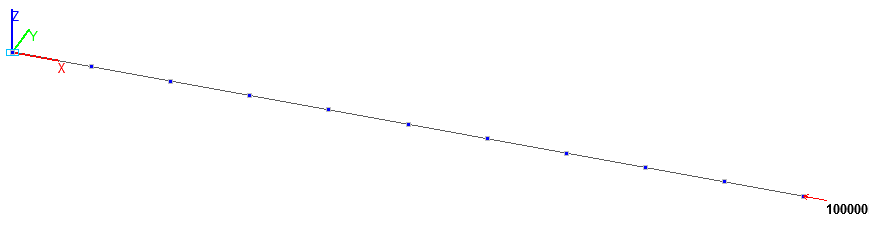
Расчетная схема. Стержневая модель

 

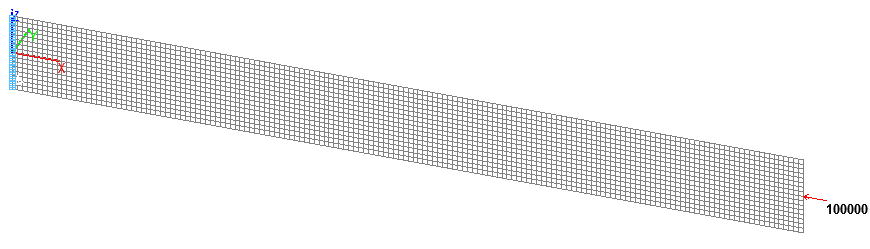
Расчетная схема. Оболочечная модель теории Рейсснера-Миндлина

 

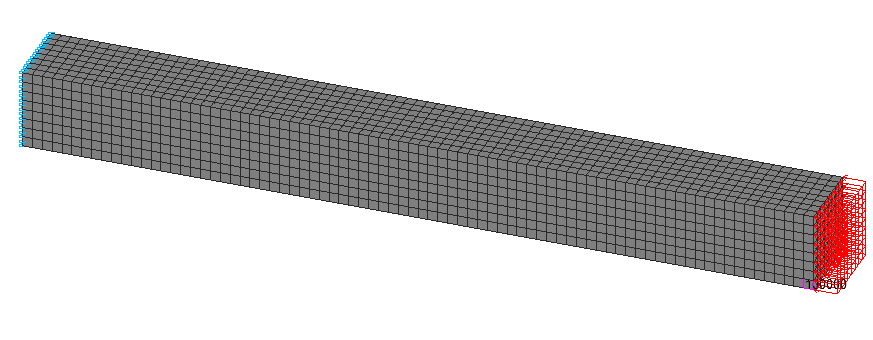
Расчетная схема. Объемная модель

 

1-ая Форма потери устойчивости. Стержневая модель

 

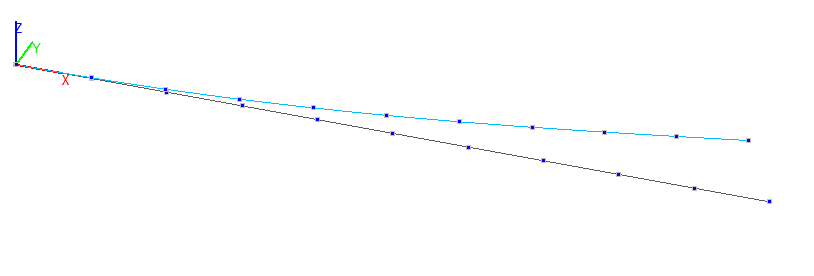
2-ая Форма потери устойчивости. Стержневая модель

 

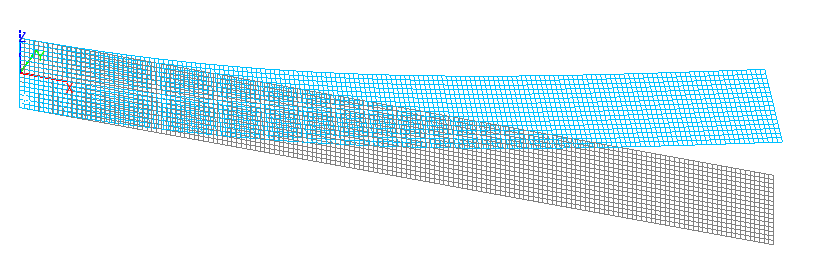
1-ая Форма потери устойчивости. Оболочечная модель теории Рейсснера-Миндлина

 

2-ая Форма потери устойчивости. Оболочечная модель теории Рейсснера-Миндлина

 

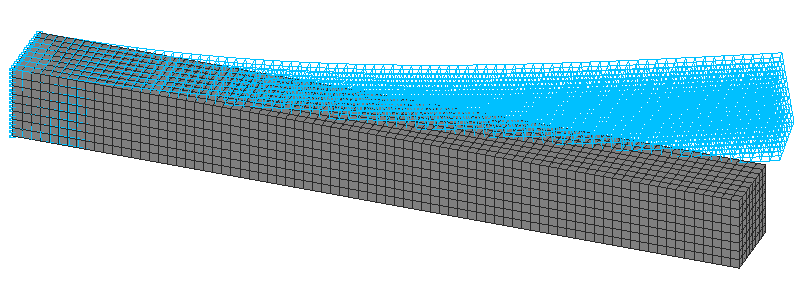
1-ая Форма потери устойчивости. Объемная модель

 

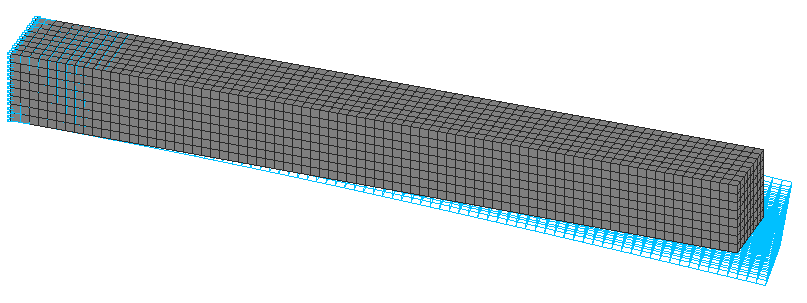
2-ая Форма потери устойчивости. Объемная модель

 

Сравнение решений:

Критические значения сосредоточенной продольной сжимающей силы P_cr1 и P_cr2 (кН), действующей центрально на свободном торце бруса

Расчетная модель	Форма потери устойчивости	Теория	SCAD	Отклонение, %
Стержневая	1-ая	61685	0,616821∙105=61682	0,01
	2-ая	61685	0,616821∙105=61682	0,01
Оболочечная теории Рейсснера-Миндлина	1-ая	61685	0,613922∙105=61392	0,48
	2-ая	61685	0,617533∙105=61753	0,11
Объемная	1-ая	61685	0,613281∙105=61328	0,58
	2-ая	61685	0,613281∙105=61328	0,58

Замечания: При аналитическом решении критические значения сосредоточенной продольной сжимающей силы P_cr1 и P_cr2, соответствующие моментам потери устойчивости консольного бруса определяются по следующим формулам:

\[ P_{cr1} =\frac{\pi^{2}\cdot E\cdot I_{y} }{4\cdot L^{2}} \quad P_{cr2} =\frac{\pi^{2}\cdot E\cdot I_{z} }{4\cdot L^{2}} \] \[ I_{y} =\frac{b\cdot h^{3}}{12} \quad I_{z} =\frac{h\cdot b^{3}}{12} \]