Устойчивость консольного бруса квадратного поперечного сечения под действием сосредоточенной поперечной изгибающей силы, центрально приложенной на свободном торце (прямой изгиб)

Цель: Определение критического значения сосредоточенной поперечной изгибающей силы, действующей центрально на свободном торце консольного бруса квадратного поперечного сечения, соответствующего моменту потери его устойчивости.

Файлы с исходными данными:

Имя файла	Описание файла расчета
Stability_Bar_2_Bar.SPR	Стержневая расчетная модель
Stability_Bar_2_Shell.SPR	Оболочечная расчетная модель
Stability_Bar_2_Solid.SPR	Объемная расчетная модель

Формулировка задачи: Консольный брус квадратного поперечного сечения подвергается воздействию сосредоточенной поперечной изгибающей силы P, центрально действующей на его свободном торце. Определить критическое значение сосредоточенной поперечной изгибающей силы P_cr, соответствующее моменту потери устойчивости консольного бруса.

Ссылки: А. С. Вольмир, Устойчивость деформируемых систем, Москва, Наука, 1967, стр.214;

Исходные данные:

L = 10.0 м	- длина консольного бруса;
h = b = 1.0 м	- сторона квадратного поперечного сечения консольного бруса;
E = 3.0·10⁷ кН/м²	- модуль упругости материала консольного бруса;
ν = 0.2	- коэффициент Пуассона;
P = 10⁵ кН	- начальное значение сосредоточенной поперечной изгибающей силы, центрально действующей на свободном торце бруса.

Конечноэлементная модель: Расчетная схема – система общего вида. Рассматриваются три расчетные модели:

Стержневая модель (С), 10 элементов типа 5, сетка конечных элементов разбита по длине продольной оси полосы с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на узел защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной поперечной изгибающей силы P задается в узле свободного торца бруса. Количество узлов в расчетной схеме – 11;

Оболочечная модель теории Рейсснера-Миндлина (П), 2560 восьмиузловых элементов типа 150, сетка конечных элементов разбита по длине продольной оси и высоте бруса с шагом 0.0625 м. Обеспечение граничных условий достигается за счет наложения связей на узлы защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной поперечной изгибающей силы P задается в узле продольной оси бруса, расположенном на свободном торце. Количество узлов в расчетной схеме – 8033.

Объемная модель (О), 5120 двадцатиузловых элементов типа 37, сетка конечных элементов разбита по длине продольной оси, ширине и высоте бруса с шагом 0.125 м. Обеспечение граничных условий достигается за счет наложения связей на узлы защемленного торца бруса по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Воздействие с начальным значением сосредоточенной поперечной изгибающей силы P задается в виде равномерно распределенной нагрузки по наружным граням элементов торца бруса p = P/(h·b). Количество узлов в расчетной схеме – 24705.

Результаты решения в SCAD

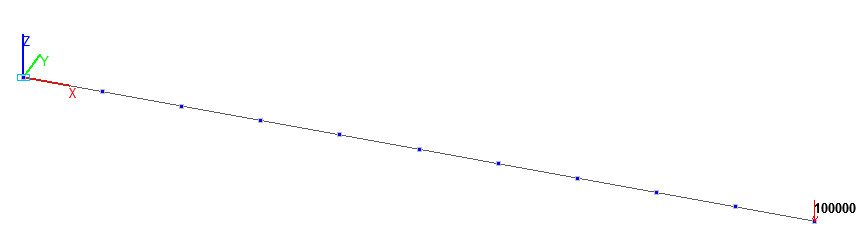
Расчетная схема. Стержневая модель

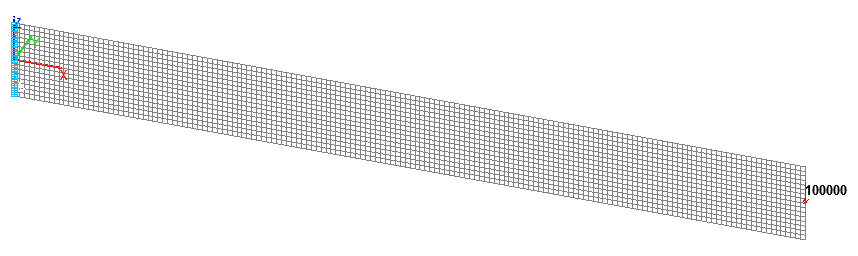
Расчетная схема. Оболочечная модель теории Рейсснера-Миндлина

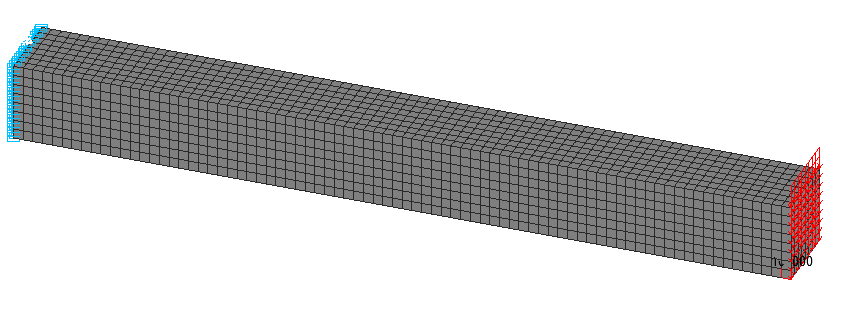
Расчетная схема. Объемная модель

1-ая Форма потери устойчивости. Стержневая модель

1-ая Форма потери устойчивости. Оболочечная модель теории Рейсснера-Миндлина

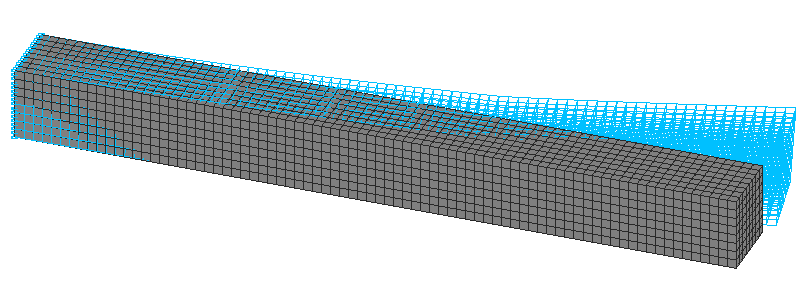
1-ая Форма потери устойчивости. Объемная модель

Сравнение решений:

Критическое значение сосредоточенной поперечной изгибающей силы P_cr (кН), действующей центрально на свободном торце бруса

Расчетная модель	Теория	SCAD	Отклонение, %
Стержневая	84111	0,834694∙10⁵=83469	0,76
Оболочечная теории Рейсснера-Миндлина	84111	0,821972∙10⁵=82197	2,28
Объемная	84111	0,843750∙10⁵=84375	0,31

Расчетная модель

Теория

SCAD

Отклонение, %

Стержневая

84111

0,834694∙10⁵=83469

0,76

Оболочечная теории

Рейсснера-Миндлина

84111

0,821972∙10⁵=82197

2,28

Объемная

84111

0,843750∙10⁵=84375

0,31

Замечания: При аналитическом решении критическое значение сосредоточенной поперечной изгибающей силы Pcr, соответствующее моменту потери устойчивости консольного бруса определяется по следующей формуле:

\[ P=\frac{4,01\cdot \sqrt {E\cdot I_{z} \cdot G\cdot I_{x} } }{L^{2}} \quad G=\frac{E}{2\cdot \left( {1+\nu } \right)} \]

\( I_{z} =\frac{h\cdot b^{3}}{12} \) – наименьший момент инерции изгиба (из плоскости действия момента);

\( I_{x} =k_{f} \cdot h\cdot b^{3} \) – момент инерции свободного кручения, где:

\[ k_{f} =\frac{1}{3}\cdot \left\{ {1-\frac{192}{\pi^{5}}\cdot \frac{b}{h}\cdot \sum\limits_{n=1}^\infty {\left[ {\sin^{2}\left( {\frac{n\cdot \pi }{2}} \right)\cdot \frac{1}{n^{5}}\cdot th\left( {\frac{n\cdot \pi \cdot h}{2\cdot b}} \right)} \right]} } \right\} \]