Консольная невесомая стойка с сосредоточенной массой на свободном торце под действием горизонтального кинематического смещения опоры (расчет по сейсмограмме)
Цель: Определение деформированного состояния консольной невесомой стойки с сосредоточенной массой на свободном торце от горизонтального кинематического воздействия на опору.
Имя файла с исходными данными: 5.14.SPR
Файл с сейсмограммой: 5.14_chart.txt
Формулировка задачи: К свободному торцу консольной невесомой стойки квадратного поперечного сечения присоединена масса m. В начальный момент времени к опоре стойки прикладывается горизонтальное кинематическое воздействие, изменяющееся по гармоническому закону Xs = Δ·sin(θ·t). Определить собственную форму и частоту колебаний ω консольной стойки, а также прогиб Xm свободного торца стойки с присоединенной массой во времени.
Ссылки: В. А. Киселев, Строительная механика. Специальный курс. Динамика и устойчивость сооружений. Москва, Стройиздат, 1980, стр. 65.
Исходные данные:
| E = 2.0·108 кН/м2 | - модуль упругости материала стойки; |
| ν = 0.3 | - коэффициент Пуассона; |
| b = 0.04 м | - ширина прямоугольного поперечного сечения стойки; |
| h = 0.04 м | - высота прямоугольного поперечного сечения стойки; |
| L = 1.0 м | - длина стойки; |
| m = 0.08 кН·с2/м | - значение сосредоточенной массы, присоединенной к свободному торцу стойки; |
| Δ = 0.1 м | - амплитудное значение кинематического гармонического возмущения, горизонтально приложенного к опоре стойки; |
| g = 10.00 м/с2 | - значение ускорения свободного падения; |
| I = b·h3/12 = 2.133333·10-7 м4 | - момент инерции поперечного сечения стойки. |
Рассматривается следующее значение частоты кинематического гармонического возмущения θ в зависимости от значения частоты собственных колебаний стойки ω: θ = 0.5·ω.
Конечноэлементная модель: Расчетная схема – система общего вида, 10 стержневых элементов типа 5. Обеспечение граничных условий достигается за счет наложения связей на узел защемленного торца стойки по направлениям степеней свободы X, Y, Z, UX, UY, UZ. Сосредоточенная масса задается преобразованием статической узловой нагрузки на свободном торце стойки m·g.
Расчет производится в два этапа: сначала модальным анализом определяется собственные форма и частота колебаний ω, затем методом прямого интегрирования уравнений движения определяется прогиб Xm свободного торца стойки с присоединенной массой во времени. Воздействие кинематического гармонического возмущения описывается графиком изменения горизонтального смещения опоры во времени и задается в виде заданного перемещения через смещение связи по оси X общей системы координат с масштабным множителем 1.0 и временем запаздывания 0.0 с. Интервалы между моментами времени графика изменения смещения равны Δtint = Tθ/100, где Tθ – период кинематического гармонического возмущения, и соответствуют шагу интегрирования. При построении графика воздействие заданного перемещения через смещение связи принимается со значениями Xs = Δ·sin(θ· n·Δtint) в моменты времени n·Δtint. Продолжительность процесса во времени равна t = 2·Tθ. Коэффициенты критического демпфирования по 1-й и 2-й собственным частотам приняты с минимальным значением ξ = 0.0001. Коэффициент пересчета для присоединенного статического загружения равен k = 0.981 (формирование масс). Количество узлов в расчетной схеме – 11. При решении используется метод модального интегрирования. Определение собственных форм и частот выполнено методом итерации подпространств. При расчете используется матрица сосредоточенных масс.
Результаты решения в SCAD


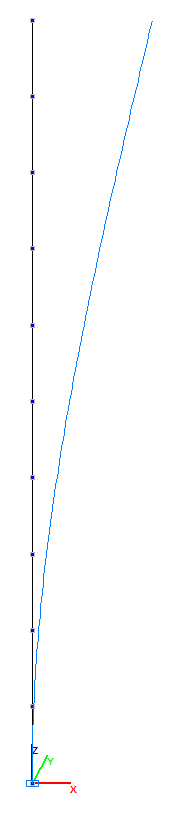
Расчетная схема и 1-я форма колебаний
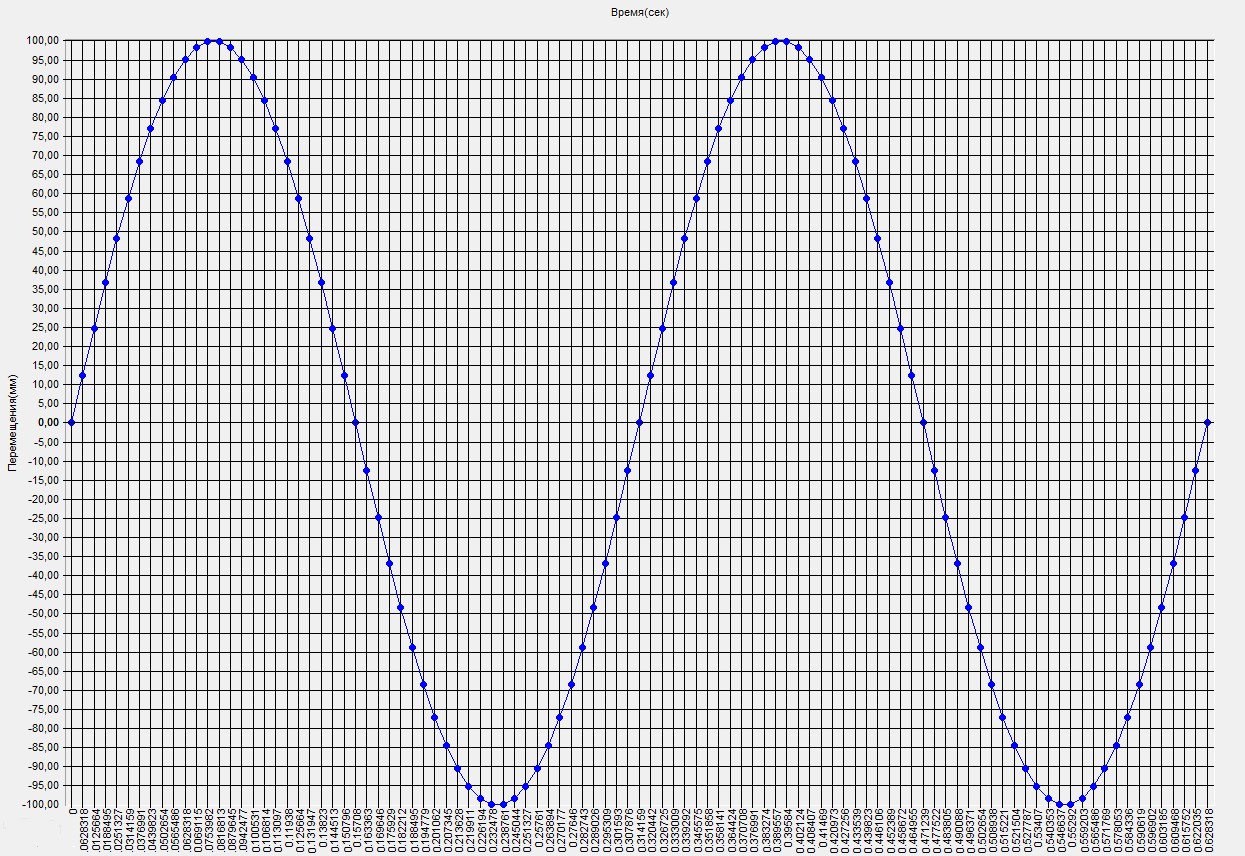
График изменения горизонтального смещение связи Xs во времени (мм).
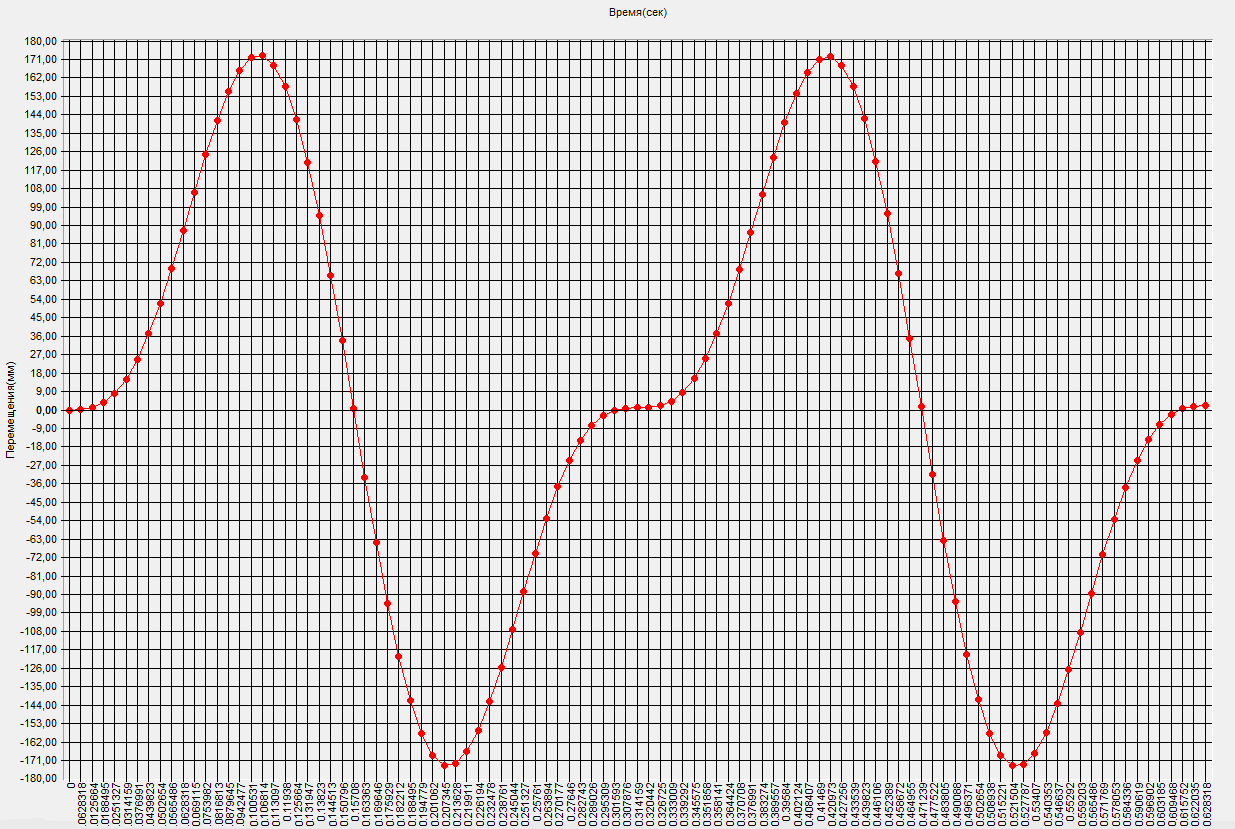
График изменения прогиба Xm свободного торца стойки с присоединенной массой во времени (мм)



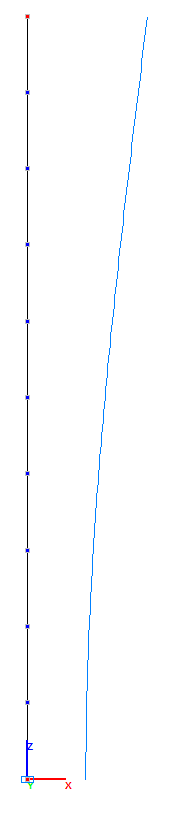



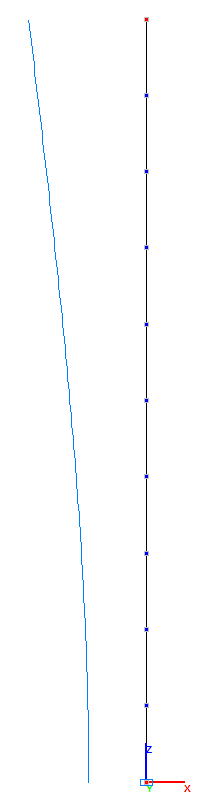



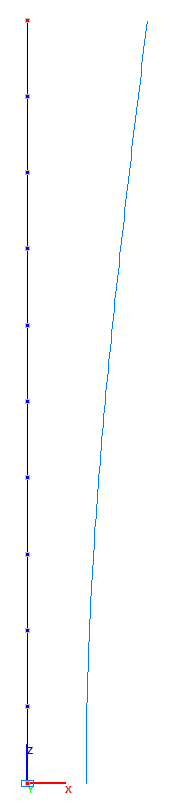



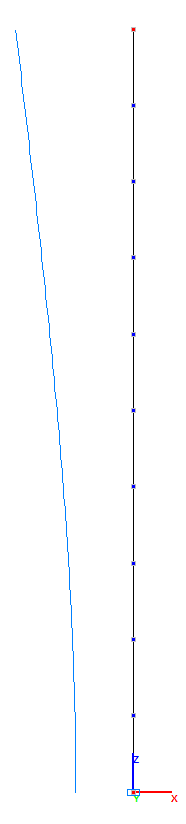


Амплитудные значения прогиба Xm свободного торца стойки с присоединенной массой и деформированные схемы в соответствующие моменты (мм).
Сравнение решений:
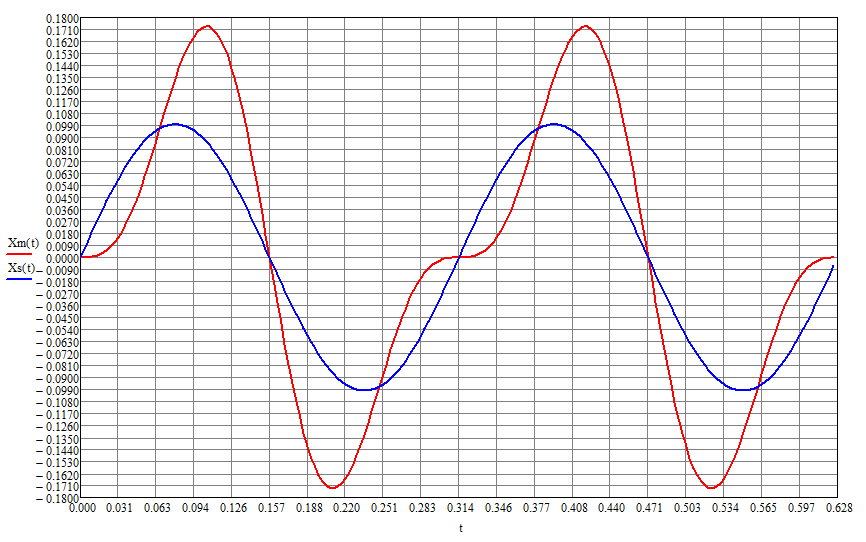
Графики изменения горизонтального смещение связи Xs и прогиба Xm свободного торца стойки с присоединенной массой во времени (м)
Частота кинематического гармонического возмущения θ = 0.5·ω
Собственная частота колебаний ω, рад/с
|
Форма колебаний |
Теория |
SCAD |
Отклонения, % |
|---|---|---|---|
|
1 |
40.000 |
40.000 |
0.00 |
Амплитудные значения прогиба Xm свободного торца стойки с присоединенной массой при частоте кинематического гармонического возмущения θ = 0.5·ω, мм
|
Теория |
SCAD |
|||
|---|---|---|---|---|
|
Время, с |
Прогиб, м |
Время, с |
Прогиб, м |
Отклонение, % |
|
0.000000 |
0.00 |
0.000000 |
0.00 |
— |
|
0.106814 |
172.90 |
0.106814 |
172.77 |
0.08 |
|
0.157080 |
0.00 |
0.157080 |
0.59 |
— |
|
0.207345 |
-172.90 |
0.207345 |
-173.21 |
0.18 |
|
0.314159 |
0.00 |
0.314159 |
1.10 |
— |
|
0.420973 |
172.90 |
0.420973 |
172.22 |
0.39 |
|
0.471239 |
0.00 |
0.471239 |
1.68 |
— |
|
0.521504 |
-172.90 |
0.521504 |
-173.58 |
0.39 |
|
0.628318 |
0.00 |
0.628318 |
2.20 |
— |
Замечания: При аналитическом решении собственная частота колебаний ω консольной стойки с сосредоточенной массой на свободном торце определяется по формуле:
\[ \omega =\sqrt {\frac{3\cdot E\cdot I}{m\cdot L^{3}}} \]
При аналитическом решении прогиб Xm свободного торца стойки с присоединенной массой во времени определяется по формуле:
\[ X_{m} \left( t \right)=\frac{\Delta }{\left( {1-\frac{\theta^{2}}{\omega ^{2}}} \right)}\cdot \left( {\sin \left( {\theta \cdot t} \right)-\frac{\theta }{\omega }\cdot \sin \left( {\omega \cdot t} \right)} \right) \]
