Двухпролетная свободно опертая балка с промежуточной податливой опорой под действием сосредоточенных поперечных сил, расположенных в середине пролетов

Цель: Определение напряженно-деформированного состояния двухпролетной свободно опертой балки с промежуточной податливой опорой под действием сосредоточенных поперечных сил, расположенных в середине пролетов.

Файл с исходными данными: SSLL03_v11.3.spr

Формулировка задачи: Двухпролетная свободно опертая балка с промежуточной податливой опорой нагружается сосредоточенными поперечными силами F, расположенными в середине пролетов (на расстоянии l от крайних опор). Определить вертикальное перемещение Z и вертикальную реакцию N промежуточной податливой опоры, а также изгибающий момент M в балке над  промежуточной податливой опорой (точка B).

Ссылки: C. Massonnet, Application des ordinateurs au calcul des structures, Paris, Eyrolles, 1968, p. 233.

Исходные данные:

E = 2.1·1011  Па	- модуль упругости,
2·l = 6.0 м	- длина пролета балки;
A = 0.4762·10-3 м2	- площадь поперечного сечения;
I = 6,3·10-4 м4	- момент инерции поперечного сечения;
k = 2.1·1011 Н/м	- жесткость промежуточной податливой опоры
F = 4.2·104 Н	- значение сосредоточенных поперечных сил.

Конечноэлементная модель: Расчетная  схема – плоская рама, 4 стержневых элемента типа 2. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы: X, Z – для левой опоры; Z – для правой опоры и введением связи конечной жесткости по направлению степени свободы Z – для промежуточной опоры (тип элемента 51). Количество узлов в расчетной схеме – 5.

Результаты решения в SCAD

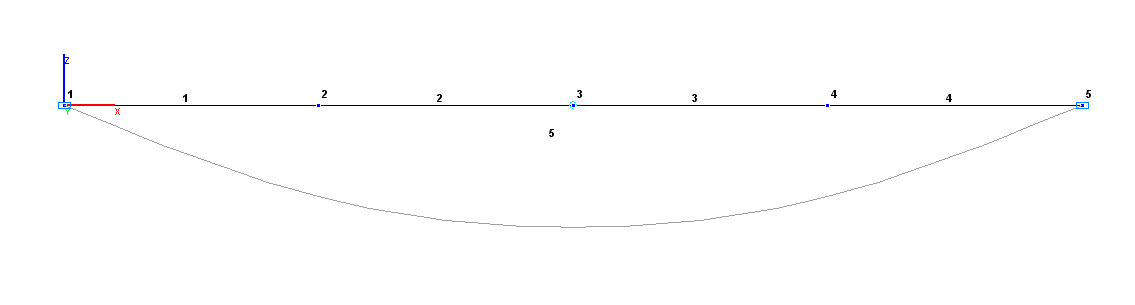
Расчетная и деформированная схемы

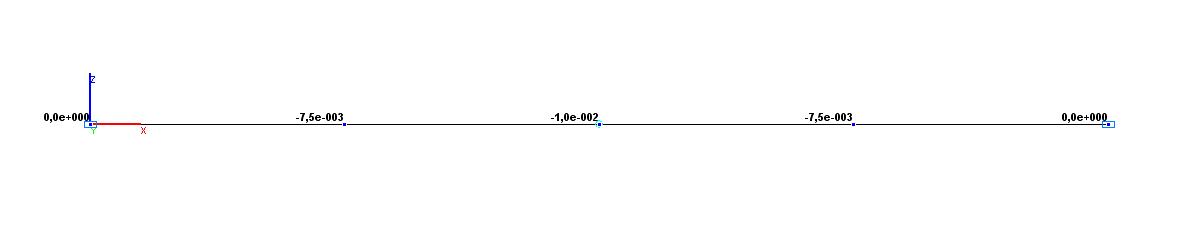
Значения вертикальных перемещений Z (м)

Значения вертикальных опорных реакций N (Н)

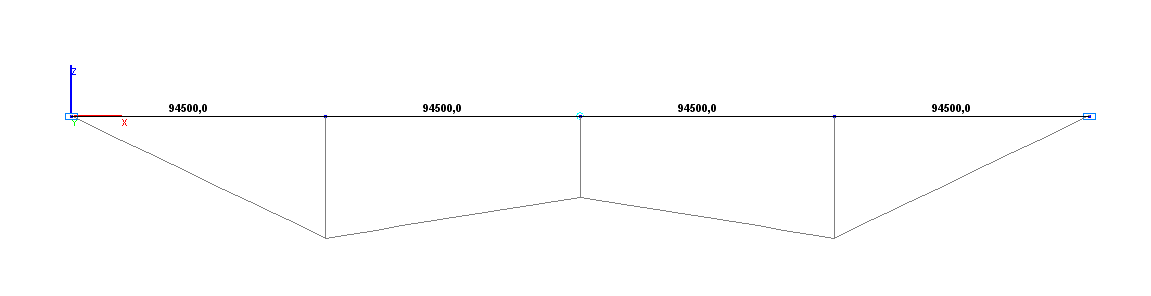
Эпюра изгибающих моментов М (кН*м)

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Вертикальное перемещение Z (точка B), м	-1.0000·10-2	-1.0000·10-2	0.00
Вертикальная реакция H (точка B), Н	21000.0	21000.0	0.00
Изгибающий момент M (точка B), Н·м	63000.0	63000.0	0.00