Расчет прочности и жесткости главных балок балочных клеток
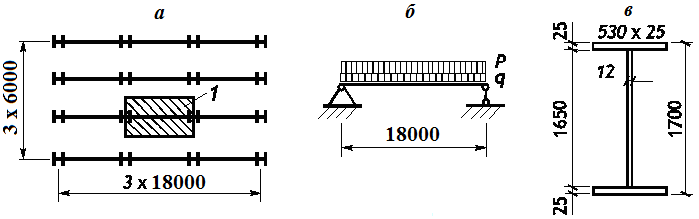
а – план перекрытия; б – расчетная схема главной балки; в – сечение балки; 1 – грузовая площадь
Цель: Проверка расчета балок в постпроцессоре «Сталь» вычислительного комплекса SCAD
Задача: Подобрать сварной двутавровый профиль для главных балок пролетом 18,0 м в балочной клетке нормального типа. Верхний пояс главных балок раскреплен по длине балками настила, расположенными с шагом 1 м.
Источник: Металлические конструкции: учебник для студ. Учреждений высш. проф. Образования / [Ю. И. Кудишин, Е. И. Беленя, В. С. Игнатьева и др.]; под. Ред. Ю. И. Кудишина. - 13-е изд., испр. - М. : Издательский центр "Академия", 2011. С 192.
Соответствие нормативным документам: СНиП II-23-81*, СП 16.13330, ДБН В.2.6-163:2010.
Имя файла с исходными данными:
3.4 Beam_Example_3.4.spr;
3.4 Beam_Example_3.4.doc — отчет
Исходные данные:
| а = 6 м | Шаг главных балок; |
| g1 = 1,16 кН/м2 | Масса настила и балок настила; |
| p = 20 кН/м2 | Временная (полезная) нагрузка; |
| qн = 127,099 кН/м | Суммарная нормативная нагрузка на балку; |
| q1 = 1,05*1,16 кН/м2 * 6 м*1,02 = 7,454 кН/м | Расчетная постоянная нагрузка; (коэффициент 1,02 учитывает собственный вес главной балки); |
| q2 = 1,2*20 кН/м2 * 6 м = 144,0 кН/м | Расчетная полезная нагрузка; |
| l = 18 м | Пролет главной балки; |
| Ry = 23 кН/cм2 Rs = 0,58*23=13,34 кН/cм2 |
Сталь марки C255 при толщине t>20 мм; |
| [ f ] = l/400 = 45 мм | Предельный прогиб; |
| bp×tp = 530×20 мм | Сечение опорного ребра; |
| kp = 6 мм | Катет углового шва в сварном соединении опорного ребра с балкой; |
| γc = 1 | Коэффициент условий работы; |
| Wy = 27153,85 см3 | Геометрические характеристики для сварного |
| Iy = 2308077,083 см4 | двутавра с полками 530×25 мм и стенкой 1650×12 мм; |
| Sy = 15180,625 см3. |
Результаты SCAD Постпроцессор СТАЛЬ:
[Элемент № 3] Усилия
|
N Макс. 0 Т |
My
|
Mz Макс. 0 Т*м |
|
Mk Макс. 0 Т*м |
Qz Макс. 69,47 Т |
Qy Макс. 0 Т |
|
|
Длина стержня 4,5 м |
|
[Элемент № 3] Прогибы
|
X |
Y |
Z
|
|
|
Длина стержня 4,5 м |
|
Расчет выполнен по СНиП II-23-81*
Конструктивный элемент main beam
Сталь: C255
Длина элемента 18 м
Предельная гибкость для сжатых элементов: 180
Предельная гибкость для растянутых элементов: 300
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Коэффициент расчетной длины XoZ -- 1
Коэффициент расчетной длины XoY -- 1
Расстояние между точками раскрепления на плоскости 1 м
Сечение
|
Результаты расчета |
Проверка |
Коэффициент использования |
|---|---|---|
|
п.5.12 |
Прочность при действии изгибающего момента My |
0,98 |
|
пп.5.12,5.18 |
Прочность при действии поперечной силы Qz |
0,56 |
|
пп.5.24,5.25 |
Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики |
0,98 |
|
п.5.15 |
Устойчивость плоской формы изгиба |
0,98 |
|
пп.6.15,6.16 |
Предельная гибкость в плоскости XoY |
0,52 |
|
пп.6.15,6.16 |
Предельная гибкость в плоскости XoZ |
0,08 |
Коэффициент использования 0,98 - Прочность при действии изгибающего момента My
Ручной расчет (СНиП II-23-81*):
1. Максимальный изгибающий момент и поперечная сила, действующие в расчетных сечениях балки:
\[ M_{\max } =\frac{q_{\Sigma } l^{2}}{8}=\frac{\left( {7,454+144} \right)\cdot 18,0^{2}}{8}=6133,887 \quad кНм. \] \[ Q_{\max } =\frac{q_{\Sigma } l}{2}=\frac{\left( {7,454+144} \right)\cdot 18,0}{2}=1363,086 \quad кН. \]
2. Необходимый момент сопротивления балки:
\[ W_{nes} =\frac{M_{\max } }{R_{y} \gamma_{c} }=\frac{6133,887\cdot 100}{23}=26669,074 \quad см^{3}. \]
3. Максимальные касательные напряжения, возникающие в опорном сечении балки:
\[ \tau_{\max } =\frac{Q_{\max } S_{y} }{I_{y} t_{w} }=\frac{1363,086\cdot 15180,625}{2308077,083\cdot 1,2}=7,471 \quadкН/см^{2}. \]
4. Максимальный прогиб, возникающий в середине пролета балки:
\[ f_{\max } =\frac{5}{384}\cdot \frac{q_{н} l^{4}}{EI_{y} }=\frac{5}{384}\cdot \frac{127,099\cdot 18,0^{4}}{2,06\cdot 10^{5}\cdot 10^{3}\cdot 2308077,083\cdot 10^{-8}}=36,539 \quad мм. \]
5. Условная предельная гибкость сжатого пояса балки:
\[ \bar{{\lambda }}_{ub} =0,35+0,0032\frac{b_{f} }{t_{f} }+\left( {0,76-0,02\frac{b_{f} }{t_{f} }} \right)\frac{b_{f} }{h_{f} }=0,35+0,0032\frac{530}{25}+\left( {0,76-0,02\frac{530}{25}} \right)\frac{530}{1675}=0,524. \]
6. Условная фактическая гибкость сжатого пояса балки:
\( \bar{{\lambda }}_{b} =\frac{l_{ef} }{b_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{1000}{530}\sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,063<\bar{{\lambda }}_{ub} =0,524 \) – проверка устойчивости не требуется.
7. Условная гибкость свеса сжатой полки балки:
\[ \bar{{\lambda }}_{f} =\frac{b_{ef} }{t_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{b_{f} -t_{w} }{2t_{f} }\sqrt {\frac{R_{y} }{E}} =\frac{530-12}{2\cdot 25}\sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,346<\bar{{\lambda }}_{uf} =0,5. \]
8. Прочность опорного ребра при смятии его торцевой поверхности (\( (R_{un} =370 \quad МПа,\), \(R_{p} =\frac{370}{1,025}=360,98 \quad МПа \) (см. табл. 1*)):
\[ N_{p} =A_{p} R_{p} =53,0\cdot 2\cdot 36,098=3826,388 \quad кН. \]
9. Условная площадь, момент инерции и гибкость опорного ребра при расчете его устойчивости:
\[ A_{red} =b_{p} t_{p} +0,65t_{w}^{2} \sqrt {\frac{E}{R_{y} }} =53,0\cdot 2,0+0,65\cdot 1,2^{2}\sqrt {\frac{2,06\cdot 10^{5}}{230}} =134,012 \quad см^{2}; \] \[ I_{p} =\frac{1}{12}\left( {t_{p} b_{p}^{3} +0,65t_{w}^{4} \sqrt {\frac{E}{R_{y} }} } \right)=\frac{1}{12}\left( {2,0\cdot 53,0^{3}+0,65\cdot 1,2^{4}\sqrt {\frac{2,06\cdot 10^{5}}{230}} } \right)=24816,1948 \quad см^{4}. \] \[ \lambda_{p} =l_{ef} \sqrt {\frac{A_{red} }{I_{p} }} =\left( {165+2,5} \right)\cdot \sqrt {\frac{134,012}{24816,1948}} =12,309; \] \[ \bar{{\lambda }}_{p} =\lambda_{p} \sqrt {\frac{R_{y} }{E}} =12,309\cdot \sqrt {\frac{230}{2,06\cdot 10^{5}}} =0,411. \]
10. Коэффициент продольного изгиба опорного ребра балки:
\[ \varphi =1-\left( {0,073-5,53\frac{R_{y} }{E}} \right)\bar{{\lambda }}_{p} \sqrt {\bar{{\lambda }}_{p} } =1-\left( {0,073-5,53\cdot \frac{230}{2,06\cdot 10^{5}}} \right)0,411\sqrt {0,411} =0,9824. \]
11. Несущая способность опорного ребра из условия обеспечения его устойчивости:
\[ N_{p,b} =\varphi A_{red} R_{y} =0,9824\cdot 134,012\cdot 23,0=3028,028 \quad кН. \]
12. Несущая способность угловых швов, крепящих опорное ребро к стенке балки:
\[ N_{f} =2\beta_{f} k_{f} l_{f} R_{wf} \gamma_{wf} =2\beta_{f} k_{f} \left( {85\beta_{f} k_{f} } \right)R_{wf} \gamma_{wf} =2\cdot 0,7\cdot 0,6\cdot \left( {85\cdot 0,7\cdot 0,6} \right)\cdot 18,0\cdot 1,0=539,784 \quad кН. \]
13. Погонная несущая способность угловых швов, крепящих полки балки к стенке:
\[ N_{f} =2\beta_{f} k_{f} R_{wf} \gamma_{wf} =2\cdot 0,7\cdot 0,8\cdot 18,0\cdot 1,0=20,16 \quad кН/см. \]
14. Погонное сдвиговое усилие, действующее на угловые швы, крепящие полки балки к стенке:
\[ T=\frac{Q_{\max } S_{yf} }{I_{y} }=\frac{1363,086\cdot 53,0\cdot 2,5\cdot 83,75}{2308077,083}=6,5535 \quad кН/см. \]
Сравнение решений:
|
Фактор |
Источник |
Ручной счет |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
Устойчивость опорного ребра |
– |
1363,086/3028,028 = 0,450 |
0,45 |
0,0 |
|
Смятие опорного ребра |
– |
1363,086/3826,388 = 0,356 |
0,357 |
0,0 |
|
Прочность поясного шва |
– |
6,5535/20,16 = 0,325 |
0,315 |
1,23% |
|
Прочность шва опорного ребра |
– |
1363,086/539,784 = 2,525 |
2,525 |
0,0 |
|
Прочность при действии поперечной силы |
0,617 |
7,471/13,34 = 0,56 |
0,56 |
0,0 |
|
Прочность при действии изгибающего момента |
1,0 |
26669,074/27153,85=0,982 |
0,982 |
0,0 |
|
Устойчивость плоской формы изгиба при действии момента |
– |
– |
0,982 |
0,0 |
|
Местная устойчивость стенки |
– |
– |
0,6 |
0,0 |
|
Местная устойчивость поясного свеса |
0,71 |
0,346/0,5 = 0,692 |
0,692 |
0,0 |
|
Максимальный прогиб |
– |
36,539/45 = 0,812 |
0,812 |
0,0 |
Комментарии:
- Проверка касательных напряжений в источнике производилась по приближенной формуле.
- Проверка местной устойчивости поясного свеса в источнике выполнена неверно.







