Гармоническое возбуждение
Цель: Сравнение вычисленного спектра ответа с точным аналитическим решением.
Файлы с исходными данными:
Sin.spc — акселерограмма
Sin.txt — списки частот
Sin.xls — сравнение результатов
sinReport.doc — отчет программы
Формулировка задачи: Рассматривается акселерограмма в виде синусоиды, то есть ускорение в момент времени t равно sin(t). Анализируется спектр ответа, вычисленный программой и полученный аналитически. Рассматривается случай, когда коэффициент затухания колебаний равен 15% от критической величины (логарифмический декремент затуханий равен 0.953263).
Сравнение решений:
Графики спектров ответа, полученные численно и аналитически, представлены на рисунке ниже
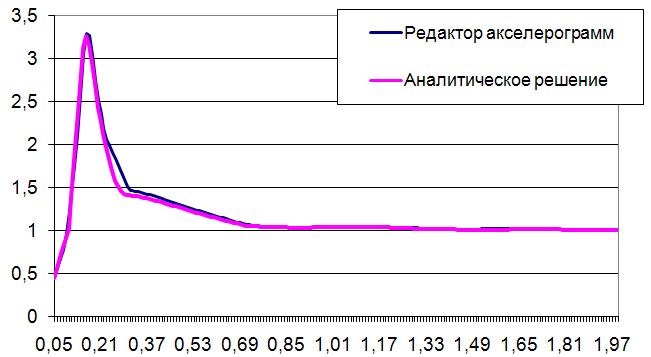
Значение максимального ускорения в обоих случаях достигаются при одной и той же частоте. Значения максимальных ускорений отличаются на 1,2%.
Замечания: Уравнение движения имеет вид
\[ \ddot{{x}}+2\beta \omega \dot{{x}}+\omega^{2}x=-a_{0} \sin (\theta t) ,\] \[ x(0)=\dot{{x}}(0)=0. \]
Аналитическое решение этого уравнения следующее
\[ x(t)=e^{-\beta \omega t}\left( {A\sin \omega_{D} t+B\cos \omega_{D} t} \right)+C\cos \theta t+D\sin \theta t ,\]
где
\[ \omega_{D} =\omega \sqrt {1-\beta^{2}} , \] \[ C=a_{0} \frac{2\beta \omega \theta }{\left( {\omega^{2}-\theta^{2}} \right)^{2}+(2\beta \omega \theta )^{2}}, \] \[ D=a_{0} \frac{\theta^{2}-\omega^{2}}{\left( {\omega^{2}-\theta^{2}} \right)^{2}+(2\beta \omega \theta )^{2}}, \] \[ B=-C, \] \[ A=-\beta C-D\theta /\omega_{D} . \]