Балка, лежащая на упругом горизонтальном основании свободно опертая по краям под действием вертикальной равномерно распределенной нагрузки, сосредоточенных вертикальной силы и изгибающего момента

Цель: Определение напряженно-деформированного состояния балки, лежащей на упругом горизонтальном основании свободно опертой по краям от воздействия вертикальной равномерно распределенной нагрузки, сосредоточенных вертикальной силы и изгибающего момента.

Файлы с исходными данными:

SSLL16_var_1_v11.3.spr	Расчетная  схема – стержневые элементы на упругом основании
SSLL16_var_2_v11.3.spr	Расчетная  схема – стержневые элементы на упругих опорах в виде элементов связей конечной жесткости типа 51

Формулировка задачи: Балка, расположенная на упругом горизонтальном основании постоянной по длине жесткости k и свободно опертая по краям, находится под воздействием вертикальной равномерно распределенной нагрузки P, сосредоточенной вертикальной силы F, приложенной в середине пролета (точка D) и сосредоточенных изгибающих моментов –C и C, приложенных по краям (точки A и B). Определить вертикальное перемещение Z в середине пролета балки (точка D), углы поворота UY краев балки (точки A и B), а также изгибающий момент M в середине пролета балки и поперечную силу Q на краю балки.

Ссылки: M. Courtand et P. Lebelle, Formulaire du beton arme, t.2, Paris, Eyrolles,1976, p. 385.

Исходные данные:

E = 2.1∙1011 Па	- модуль упругости;
l = 0.5∙π∙(10.0)0.5 = 4.967294133 м	- длина балки;
b = 1.0 м	- ширина основания балки;
Iy = 1.0∙10-4 м4	- момент инерции поперечного сечения балки;
kz = 8.4∙105 Н/м3	- коэффициент упругого основания балки;
P = 5.0∙103 Н/м	- значение вертикальной равномерно распределенной нагрузки;
F = 1.0∙104 Н	- значение сосредоточенной вертикальной силы;
C = 1.5∙104 Н∙м	- значение сосредоточенного изгибающего момента.

Конечноэлементная модель: Рассматривается два варианта расчетной схемы.

Вариант 1:

Расчетная  схема – балочный ростверк / плита, 24 стержневых элемента типа 3 на упругом основании с направлением по оси Z1 местной системы координат. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z для шарнирно-подвижных опорных узлов. Количество узлов в расчетной схеме – 25.

Вариант 2:

Расчетная  схема – балочный ростверк / плита, 24 стержневых элемента типа 3 на упругих опорах в виде 25 элементов связей конечной жесткости типа 51 с направлением по оси Z общей системы координат. Жесткость промежуточных упругих опор составляет: k_z∙b∙l/24 = 173855 Н/м, жесткость крайних упругих опор составляет: 0.5∙k_z∙b∙l/12 = 86928 Н/м. Обеспечение граничных условий достигается за счет наложения связей по направлению степени свободы Z для шарнирно-подвижных опорных узлов. С целью предотвращения геометрической изменяемости системы по оси симметрии балки устанавливается связь по направлению степени свободы UX и вводится минимальная жесткость балки на кручение GI_x = 1.0 Н∙м². Количество узлов в расчетной схеме – 25;

Результаты решения в SCAD

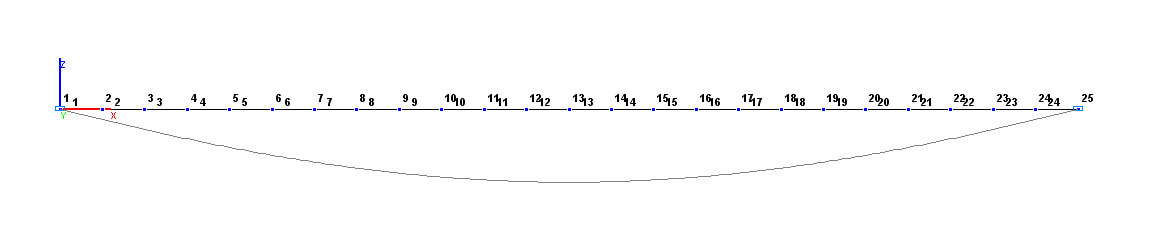
Расчетная и деформированная схемы. Вариант 1

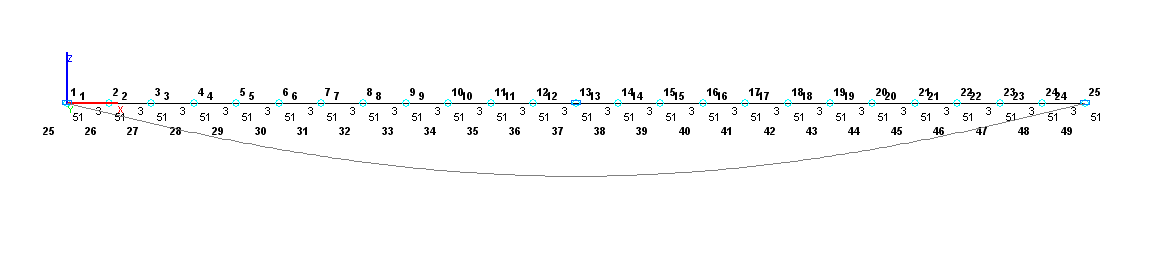
Значения Расчетная и деформированная схемы. Вариант 2

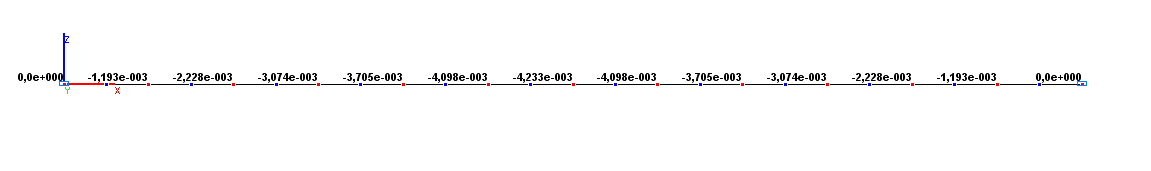
Значения вертикальных перемещений Z (м) для расчетной схемы по варианту 1

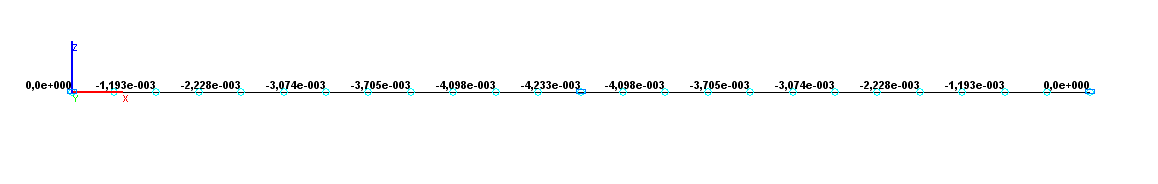
Значения вертикальных перемещений Z (м) для расчетной схемы по варианту 2

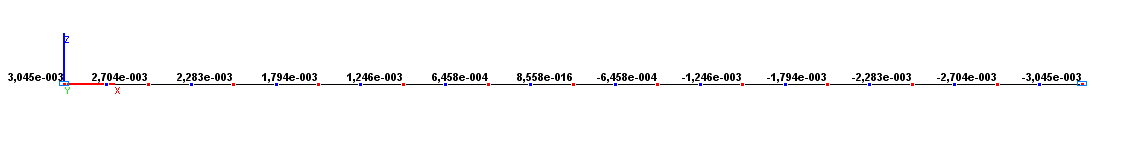
Значения углов поворота UY (рад) для расчетной схемы по варианту 1

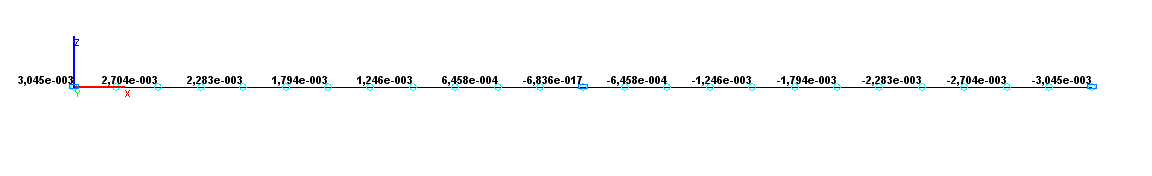
Значения углов поворота UY (рад) для расчетной схемы по варианту 2

Значения изгибающих моментов M (Н•м) для расчетной схемы по варианту 1

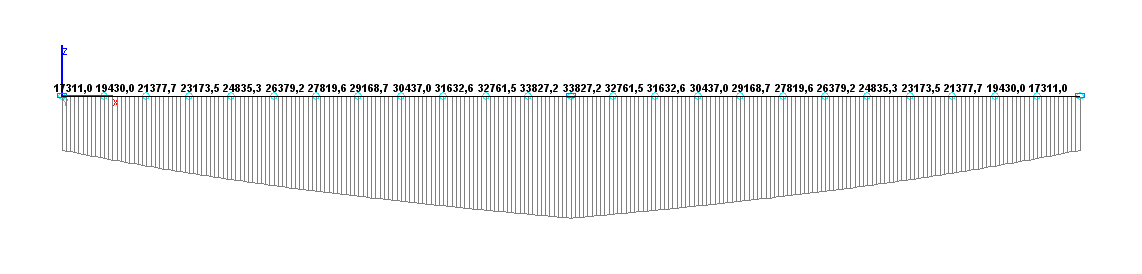
Значения изгибающих моментов M (Н•м) для расчетной схемы по варианту 2

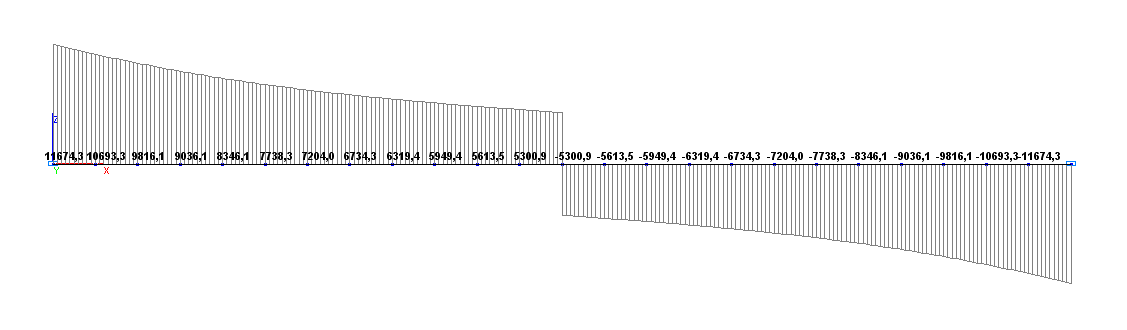
Значения поперечных сил Q (Н) для расчетной схемы по варианту 1

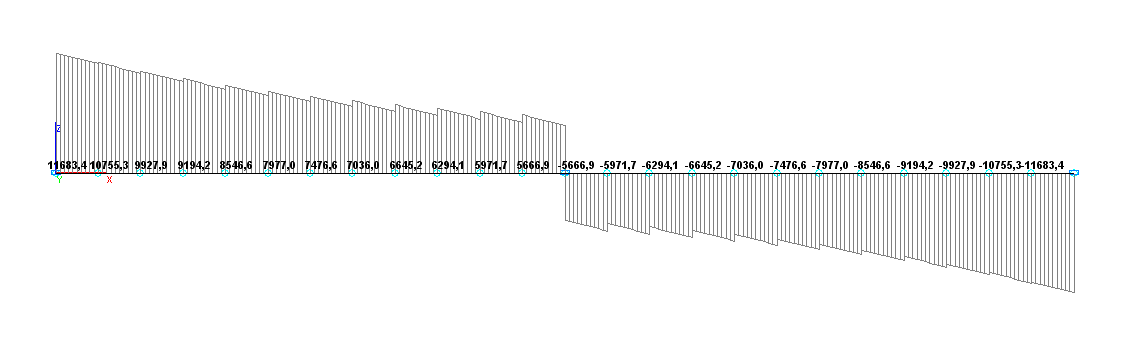
Значения поперечных сил Q (Н) для расчетной схемы по варианту 2

Сравнение решений:

Параметр	Теория	SCAD РС по варианту 1	Отклонения, %	SCAD РС по варианту 2	Отклонения, %
Вертикальное перемещение ZD, м	-4.233•10-3	-4.233•10-3	0.00	-4.233•10-3	0.00
Угол поворота UYA, рад	3.045•10-3	3.045•10-3	0.00	3.045•10-3	0.00
Изгибающий момент MD, Н•м	33840.0	33839.9	0.00	33827.2	0.04
Поперечная сила QA, Н	11674.0	11674.3	0.00	11683.4	0.08